Librerías auxiliares

• En este tema se usarán las siguientes librerías:

import Data.Char

1 Recursión numérica

Recursión numérica: El factorial

• La función factorial:

factorial :: Integer -> Integer
factorial 0 = 1
factorial n = n * factorial (n-1)

• Cálculo:

factorial 3
= 3 * (factorial 2)
= 3 * (2 * (factorial 1))
= 3 * (2 * (1 * (factorial 0)))
= 3 * (2 * (1 * 1))
= 3 * (2 * 1)
= 3 * 2
= 6

Recursión numérica: El producto

• Definición recursiva del producto:

por :: Int -> Int -> Int
m `por` 0  = 0
m `por` n  = m + (m `por` (n-1))

• Cálculo:

3 `por` 2
= 3 + (3 `por` 1)
= 3 + (3 + (3 `por` 0))
= 3 + (3 + 0)
= 3 + 3
= 6

2 Recusión sobre lista

Recursión sobre listas: La función product

• Producto de una lista de números:

product :: Num a => [a] -> a
product []     = 1
product (n:ns) = n * product ns

• Cálculo:

product [7,5,2]
= 7 * (product [5,2])
= 7 * (5 * (product [2]))
= 7 * (5 * (2 * (product [])))
= 7 * (5 * (2 * 1))
= 7 * (5 * 2)
= 7 * 10
= 70

Recursión sobre listas: La función length

• Longitud de una lista:

length :: [a] -> Int
length []     = 0
length (_:xs) = 1 + length xs

• Cálculo:

length [2,3,5]
= 1 + (length [3,5])
= 1 + (1 + (length [5]))
= 1 + (1 + (1 + (length [])))
= 1 + (1 + (1 + 0))
= 1 + (1 + 1)
= 1 + 2
= 3

Recursión sobre listas: La función reverse

• Inversa de una lista:

reverse :: [a] -> [a]
reverse []     = []
reverse (x:xs) = reverse xs ++ [x]

• Cálculo:

reverse [2,5,3]
= (reverse [5,3]) ++ [2]
= ((reverse [3]) ++ [5]) ++ [2]
= (((reverse []) ++ [3]) ++ [5]) ++ [2]
= (([] ++ [3]) ++ [5]) ++ [2]
= ([3] ++ [5]) ++ [2]
= [3,5] ++ [2]
= [3,5,2]

Recursión sobre listas: ++

• Concatenación de listas:

(++) :: [a] -> [a] -> [a]
[]     ++ ys = ys
(x:xs) ++ ys = x : (xs ++ ys)

• Cálculo:

[1,3,5] ++ [2,4]
= 1:([3,5] ++ [2,4])
= 1:(3:([5] ++ [2,4]))
= 1:(3:(5:([] ++ [2,4])))
= 1:(3:(5:[2,4]))
= 1:(3:[5,2,4])
= 1:[3,5,2,4]
= [1,3,5,2,4]

Recursión sobre listas: Inserción ordenada

• (inserta e xs) inserta el elemento e en la lista xs delante del primer elemento de xs mayor o igual que e. Por ejemplo,

inserta 5 [2,4,7,3,6,8,10] == [2,4,5,7,3,6,8,10]

inserta :: Ord a => a -> [a] -> [a]
inserta e []                  = [e]
inserta e (x:xs) | e <= x     = e : (x:xs)
                 | otherwise  = x : inserta e xs

• Cálculo:

inserta 4 [1,3,5,7]
= 1:(inserta 4 [3,5,7])
= 1:(3:(inserta 4 [5,7]))
= 1:(3:(4:(5:[7])))
= 1:(3:(4:[5,7]))
= [1,3,4,5,7]

Recursión sobre listas: Ordenación por inserción

• (ordena_por_insercion xs) es la lista xs ordenada mediante inserción, Por ejemplo,

ordena_por_insercion [2,4,3,6,3] == [2,3,3,4,6]

ordena_por_insercion :: Ord a => [a] -> [a]
ordena_por_insercion []     = []
ordena_por_insercion (x:xs) =
    inserta x (ordena_por_insercion xs)

• Cálculo:

  ordena_por_insercion [7,9,6] =
= inserta 7 (inserta 9 (inserta 6 []))
= inserta 7 (inserta 9 [6])
= inserta 7 [6,9]
= [6,7,9]

3 Recursión sobre varios argumentos

Recursión sobre varios argumentos: La función zip

• Emparejamiento de elementos (la función zip):

zip :: [a] -> [b] -> [(a, b)]
zip []     _      = []
zip _      []     = []
zip (x:xs) (y:ys) = (x,y) : zip xs ys

• Cálculo:

zip [1,3,5] [2,4,6,8]
= (1,2) : (zip [3,5] [4,6,8])
= (1,2) : ((3,4) : (zip [5] [6,8]))
= (1,2) : ((3,4) : ((5,6) : (zip [] [8])))
= (1,2) : ((3,4) : ((5,6) : []))
= [(1,2),(3,4),(5,6)]

Recursión sobre varios argumentos: La función drop

• Eliminación de elementos iniciales:

drop :: Int -> [a] -> [a]
drop 0 xs     = xs
drop n []     = []
drop n (x:xs) = drop (n-1) xs

• Cálculo:

drop 2 [5,7,9,4]       |        drop 5 [1,4]
= drop 1 [7,9,4]       |        = drop 4 [4]
= drop 0 [9,4]         |        = drop 1 []
= [9,4]                |        = []

4 Recursión múltiple

Recursión múltiple: La función de Fibonacci

• La sucesión de Fibonacci es: 0,1,1,2,3,5,8,13,21,. Sus dos primeros términos son 0 y 1 y los restantes se obtienen sumando los dos anteriores.

• (fibonacci n) es el n-ésimo término de la sucesión de Fibonacci. Por ejemplo,

fibonacci 8  ==  21

fibonacci :: Int -> Int
fibonacci 0 = 0
fibonacci 1 = 1
fibonacci n = fibonacci (n-2) + fibonacci (n-1)

Recursión múltiple: Ordenación rápida

• Algoritmo de ordenación rápida:

ordena :: (Ord a) => [a] -> [a]
ordena [] = []
ordena (x:xs) =
    (ordena menores) ++ [x] ++ (ordena mayores)
    where menores = [a | a <- xs, a <= x]
          mayores = [b | b <- xs, b > x]

5 Recursión mutua

Recursión mutua: Par e impar

• Par e impar por recursión mutua:

par :: Int -> Bool
par 0 = True
par n = impar (n-1)

impar :: Int -> Bool
impar 0 = False
impar n = par (n-1)

• Cálculo:

impar 3               |         par 3
= par 2               |         = impar 2
= impar 1             |         = par 1
= par 0               |         = impar 0
= True                |         = False

Recursión mutua: Posiciones pares e impares

• (pares xs) son los elementos de xs que ocupan posiciones pares.

• (impares xs) son los elementos de xs que ocupan posiciones impares.

pares :: [a] -> [a]
pares []     = []
pares (x:xs) = x : impares xs

impares :: [a] -> [a]
impares []     = []
impares (_:xs) = pares xs

• Cálculo:

  pares [1,3,5,7]
  = 1:(impares [3,5,7])
  = 1:(pares [5,7])
  = 1:(5:(impares [7]))
  = 1:(5:[])
  = [1,5]

6 Heurísticas para las definiciones recursivas

Aplicación del método: La función product

• Paso 1: Definir el tipo:

product :: [Int] -> Int

• Paso 2: Enumerar los casos:

product :: [Int] -> Int
product []     =
product (n:ns) =

• Paso 3: Definir los casos simples:

product :: [Int] -> Int
product []     = 1
product (n:ns) =

• Paso 4: Definir los otros casos:

product :: [Int] -> Int
product []     = 1
product (n:ns) = n * product ns

• Paso 5: Generalizar y simplificar:

product :: Num a => [a] -> a
product []     = 1
product (n:ns) = n * product ns

Aplicación del método: La función drop

• Paso 1: Definir el tipo:

drop :: Int -> [a] -> [a]

• Paso 2: Enumerar los casos:

drop :: Int -> [a] -> [a]
drop 0 []     =
drop 0 (x:xs) =
drop n []     =
drop n (x:xs) =

• Paso 3: Definir los casos simples:

drop :: Int -> [a] -> [a]
drop 0 []     = []
drop 0 (x:xs) = x:xs
drop n []     = []
drop n (x:xs) =

• Paso 4: Definir los otros casos:

drop :: Int -> [a] -> [a]
drop 0 []     = []
drop 0 (x:xs) = x:xs
drop n []     = []
drop n (x:xs) = drop n xs

• Paso 5: Generalizar y simplificar:

drop :: Integral b => b -> [a] -> [a]
drop 0 xs     = xs
drop n []     = []
drop n (_:xs) = drop n xs

Aplicación del método: La función init

• init elimina el último elemento de una lista no vacía.

• Paso 1: Definir el tipo:

init :: [a] -> [a]

• Paso 2: Enumerar los casos:

init :: [a] -> [a]
init (x:xs) =

• Paso 3: Definir los casos simples:

init :: [a] -> [a]
init (x:xs) | null xs   = []
            | otherwise =

• Paso 4: Definir los otros casos:

init :: [a] -> [a]
init (x:xs) | null xs   = []
            | otherwise = x : init xs

• Paso 5: Generalizar y simplificar:

init :: [a] -> [a]
init [_]    = []
init (x:xs) = x : init xs

7 Recursión y dibujos

• En esta sección se amplían los programas de dibujo con CodeWorld/Haskell estudiados en el tema 0 y tema 5.

7.1 Fractal del árbol

• Ejemplo: Escribir un programa para pintar el siguiente dibujo

• Programa

import CodeWorld

main :: IO ()
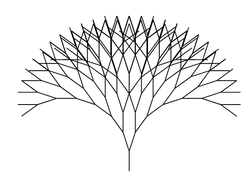
main = drawingOf (arbol 8)

tronco :: Picture
tronco = polyline [(0,0),(0,1)]

arbol :: Integer -> Picture
arbol 0 = tronco
arbol n = tronco & rama1 & rama2
  where rama  = arbol (n-1)
        rama1 = translated 0 1 (rotated ( pi/10) rama)
        rama2 = translated 0 1 (rotated (-pi/10) rama)

• Ejemplo: Escribir un programa para pintar la siguiente animación

• Programa

import CodeWorld

main :: IO ()
main = animationOf (arbol 8 . sin)

tronco :: Picture
tronco = polyline [(0,0),(0,1)]

arbol :: Integer -> Double -> Picture
arbol 0 _ = tronco
arbol n f = tronco & rama1 & rama2
  where rama  = arbol (n-1) f
        rama1 = translated 0 1 (rotated ( f*pi/10) rama)
        rama2 = translated 0 1 (rotated (-f*pi/10) rama)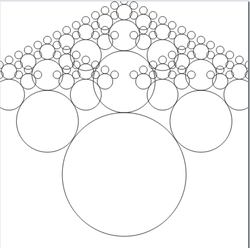

7.2 Fractal de círculos

• Ejemplo: Escribir un programa para pintar el siguiente dibujo

• Programa

import CodeWorld

main :: IO ()
main = drawingOf (arbol 4)

tronco :: Picture
tronco = translated 0 (-4) (circle 5)

arbol :: Integer -> Picture
arbol 0 = tronco
arbol n = tronco & rama1 & rama2 & rama3
  where rama  = scaled (1/2) (1/2) (arbol (n-1))
        rama1 = translated (-6.2) 2.3 rama
        rama2 = translated      0 5.5 rama
        rama3 = translated    6.2 2.3 rama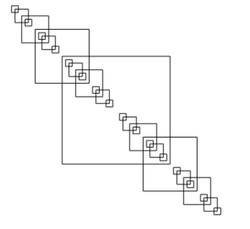

7.3 Fractal de cuadrados

• Ejemplo: Escribir un programa para pintar el siguiente dibujo

• Programa

import CodeWorld

main :: IO ()
main = drawingOf (arbol 4)

tronco :: Picture
tronco = rectangle 6 6

arbol :: Integer -> Picture
arbol 0 = tronco
arbol n = tronco & rama1 & rama2
  where rama  = scaled (1/2) (1/2) (arbol (n-1))
        rama1 = translated (-3)   3  rama
        rama2 = translated   3  (-3) rama

7.4 Fractal de cuadrados con 4 ramas

• Ejemplo: Escribir un programa para pintar el siguiente dibujo

• Programa

import CodeWorld

main :: IO ()
main = drawingOf (arbol 5)

tronco :: Picture
tronco = rectangle 10 10

arbol :: Integer -> Picture
arbol 0 = tronco
arbol n = tronco & rama1 & rama2 & rama3 & rama4 
  where rama  = scaled (1/2) (1/2) (arbol (n-1))
        rama1 = translated (-5)   5  rama
        rama2 = translated   5  (-5) rama
        rama3 = translated (-5) (-5) rama
        rama4 = translated   5    5  rama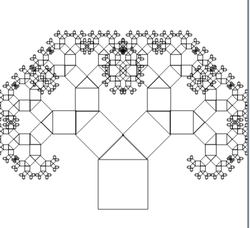

7.5 Fractal del sobre

• Ejemplo: Escribir un programa para pintar el siguiente dibujo

• Programa

import CodeWorld

main :: IO ()
main = drawingOf (arbol 8)

tronco :: Picture
tronco = translated 0 (-5) (rectangle 4 4 &
                            polyline [(-2, 2), (0, 4), (2, 2)])

arbol :: Integer -> Picture
arbol 0 = tronco
arbol n = tronco & rama1 & rama2
  where rama  = scaled r r (arbol (n-1))
        rama1 = translated   4.3  1.4 (rotated (-pi/4) rama)
        rama2 = translated (-4.3) 1.4 (rotated ( pi/4) rama)
        r     = 0.685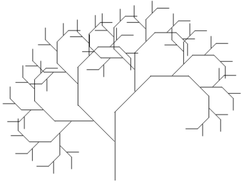

7.6 Fractal asimétrico

• Ejemplo: Escribir un programa para pintar el siguiente dibujo

• Programa

import CodeWorld

main :: IO ()
main = drawingOf (arbol 6)

tronco :: Picture
tronco = polyline [(0,-5),(0,0)]

arbol :: Integer -> Picture
arbol 0 = tronco
arbol n = tronco & rama1 & rama2
  where rama  = scaled (3/4) (3/4) (arbol (n-1))
        rama1 = translated (-2.7) 0.5 (rotated ( pi/4) rama)
        rama2 = translated   2.6  2.6 (rotated (-pi/4) rama)

8 Bibliografía

• R. Bird. Introducción a la programación funcional con Haskell. Prentice Hall, 2000.
  • Cap. 3: Números.
  • Cap. 4: Listas.
• G. Hutton. Programming in Haskell. Cambridge University Press, 2007.
  • Cap. 6: Recursive functions.
• B. O'Sullivan, D. Stewart y J. Goerzen. Real World Haskell. O'Reilly, 2008.
  • Cap. 2: Types and Functions.
• B.C. Ruiz, F. Gutiérrez, P. Guerrero y J.E. Gallardo. Razonando con Haskell. Thompson, 2004.
  • Cap. 2: Introducción a Haskell.
  • Cap. 6: Programación con listas.
• S. Thompson. Haskell: The Craft of Functional Programming, Second Edition. Addison-Wesley, 1999.
  • Cap. 4: Designing and writing programs.
• CodeWorld @ Parkside