**IAIC**
Julia
Manual rápido de Programación
[Julia](http://julialang.org) es un lenguaje de programación científica gratuito y de código abierto. Es un lenguaje relativamente nuevo que se inspira en lenguajes como Python, MATLAB y R. Se seleccionó para su uso en el curso porque es lo suficientemente de alto nivel (a diferencia de lenguajes como C++, Julia no requiere que los programadores se preocupen por la gestión de la memoria y otros detalles de bajo nivel, aunque permite el control de bajo nivel cuando es necesario) para que los algoritmos puedan expresarse de forma compacta y legible, a la vez que son rápidos (a diferencia de otros lenguajes de alto nivel, como Python, que solo pueden competir en velocidad apoyándose en librerías externas que dificultan la comprensión del código). En esta entrada introducimos los conceptos necesarios para entender el código usado en los disintos temas del curso, omitiendo muchas de las características avanzadas del lenguaje.
# Tipos
Julia tiene una variedad de tipos básicos que pueden representar datos dados como valores de verdad, números, cadenas, matrices, tuplas y diccionarios. Los usuarios también pueden definir sus propios tipos. Esta sección explica cómo utilizar algunos de los tipos básicos y cómo definir nuevos tipos.
## Booleanos
El tipo booleano en Julia, escrito como `Bool`, incluye los valores `true` y `false`. Podemos asignar estos valores a las variables. Los nombres de las variables pueden ser cualquier cadena de caracteres, incluyendo Unicode, con algunas restricciones.
~~~~
α = true
done = false
~~~~
El nombre de la variable aparece a la izquierda del signo igual; el valor que se va a asignar a la variable está a la derecha.
Podemos hacer asignaciones en la consola de Julia. La consola, o REPL (por read, eval, print, loop), devolverá una respuesta a la expresión evaluada. El símbolo `#` indica que el resto de la línea es un comentario.
~~~~
julia> x = true
true
julia> y = false; # El punto y coma suprime la salida de la consola
julia> typeof(x)
Bool
julia> x == y # test de igualdad
false
~~~~
Se admiten los operadores booleanos habituales:
~~~~
julia> !x # not
false
julia> x && y # and
false
julia> x || y # or
true
~~~~
## Números
Julia soporta números enteros y de punto flotante, como se muestra aquí:
~~~~
julia> typeof(42)
Int64
julia> typeof(42.0)
Float64
~~~~
Aquí, `Int64` denota un entero de 64 bits, y `Float64` denota un valor de punto flotante de 64 bits. Podemos realizar las operaciones matemáticas estándar:
~~~~
julia> x = 4
4
julia> y = 2
2
julia> x + y
6
julia> x - y
2
julia> x * y
8
julia> x / y
2.0
julia> x ^ y # exponenciación
16
julia> x % y # resto de la división
0
julia> div(x, y) # La división truncada devuelve un número entero
2
~~~~
Ten en cuenta que el resultado de `x / y` es un `Float64`, incluso cuando `x` e `y` son enteros. También podemos realizar estas operaciones al mismo tiempo que una asignación. Por ejemplo, `x += 1` es la abreviatura de `x = x + 1`.
También podemos hacer comparaciones:
~~~~
julia> 3 > 4
false
julia> 3 >= 4
false
julia> 3 ≥ 4 # unicode también funciona, usa \ge[tab] en la consola
false
julia> 3 < 4
true
julia> 3 <= 4
true
julia> 3 ≤ 4 # unicode también funciona, usa \le[tab] en la consola
true
julia> 3 == 4
false
julia> 3 < 4 < 5
true
~~~~
## Cadenas
Una cadena es un array de caracteres. Las cadenas no se utilizan mucho en este curso, excepto para informar de ciertos errores. Un objeto de tipo `String` puede ser construido usando caracteres `"` . Por ejemplo:
~~~~
julia> x = "optimal"
"optimal"
julia> typeof(x)
String
~~~~
## Símbolos
Un símbolo representa un identificador. Puede escribirse con el operador `:` o construirse a partir de cadenas:
~~~~
julia> :A
:A
julia> :Battery
:Battery
julia> Symbol("Failure")
:Failure
~~~~
## Vectores
Un vector es una matriz unidimensional que almacena una secuencia de valores. Podemos construir un vector utilizando corchetes, separando los elementos por comas:
~~~~
julia> x = []; # vector vacío
julia> x = trues(3); # Vector booleano que contiene tres trues
julia> x = ones(3); # vector de tres 1s
julia> x = zeros(3); # vector de tres 0s
julia> x = rand(3); # vector de tres números aleatorios entre 0 y 1
julia> x = [3, 1, 4]; # vector de enteros
julia> x = [3.1415, 1.618, 2.7182]; # vector de flotantes
~~~~
Se puede utilizar el método de comprensión para crear vectores. Para ello, se recorre una colección (posiblemente con filtrado) con el fin de operar sobre sus elementos y generar un vector nuevo:
~~~~
julia> [sin(x) for x in 1:5]
5-element Vector{Float64}:
0.8414709848078965
0.9092974268256817
0.1411200080598672
-0.7568024953079282
-0.9589242746631385
julia> [x for x in 1:10 if x%2==0]
5-element Vector{Int64}:
2
4
6
8
10
~~~~
Podemos inspeccionar el tipo de un vector (obsérvese que un vector es un alias para un tipo de array):
~~~~
julia> typeof([3, 1, 4]) # Matriz unidimensional de Int64s
Vector{Int64} (alias for Array{Int64, 1})
julia> typeof([3.1415, 1.618, 2.7182]) # Matriz unidimensional de Float64s
Vector{Float64} (alias for Array{Float64, 1})
julia> Vector{Float64} # alias para un array unidimensionalalias para un array unidimensional
Vector{Float64} (alias for Array{Float64, 1})
~~~~
La forma más común de acceder a los elementos de un vector es por medio del índice de sus elementos. Indexamos en vectores utilizando corchetes, y **el índice comienza en 1**:
~~~~
julia> x[1] # el primer elemento está indexado por 1
3.1415
julia> x[3] # tercer elemento
2.7182
julia> x[end] # usa end para referirse al final de la matriz
2.7182
julia> x[end-1] # esto devuelve el penúltimo elementoesto devuelve el penúltimo elemento
1.618
~~~~
Podemos extraer un rango de elementos de un array. Los rangos se especifican utilizando la notación de dos puntos:
~~~~
julia> x = [1, 2, 5, 3, 1]
5-element Vector{Int64}:
1
2
5
3
1
julia> x[1:3] # saca los tres primeros elementos
3-element Vector{Int64}:
1
2
5
julia> x[1:2:end] # saca todos los demás elementos
3-element Vector{Int64}:
1
5
1
julia> x[end:-1:1] # saca todos los elementos en orden inverso
5-element Vector{Int64}:
1
3
5
2
1
~~~~
### Operaciones que mutan valores
Podemos realizar diversas operaciones con matrices. En general, el signo de exclamación al final de los nombres de las funciones se utiliza para indicar que la función muta (es decir, cambia) la entrada:
~~~~
julia> length(x)
5
julia> [x, x] # vector de vectores
2-element Vector{Vector{Int64}}:
[1, 2, 5, 3, 1]
[1, 2, 5, 3, 1]
julia> push!(x, -1) # añade un elemento al final
6-element Vector{Int64}:
1
2
5
3
1
-1
julia> pop!(x) # elimina un elemento del final
-1
julia> append!(x, [2, 3]) # concatena [2, 3] al final de x
7-element Vector{Int64}:
1
2
5
3
1
2
3
julia> sort!(x) # ordena los elementos, alterando el mismo vector
7-element Vector{Int64}:
1
1
2
2
3
3
5
julia> sort(x); # ordena los elementos como un nuevo vector
julia> x[1] = 2; print(x) # cambia el primer elemento a 2
[2, 1, 2, 2, 3, 3, 5]
julia> x = [1, 2];
julia> y = [3, 4];
julia> x + y # sumar vectores
2-element Vector{Int64}:
4
6
julia> 3x - [1, 2] # multiplica por un escalar y resta
2-element Vector{Int64}:
2
4
julia> using LinearAlgebra
julia> dot(x, y) # producto escalar disponible después de usar LinearAlgebra
11
julia> x⋅y # producto escalar utilizando el carácter unicode, usa \cdot[tab] en la consola
11
julia> prod(y) # producto de todos los elementos de y
12
~~~~
### Aplicación punto a punto
A menudo es útil aplicar las funciones elemento a elemento a los vectores, lo que llama también **broadcasting**. Con los operadores infijos (p. ej., `+`, `*` y `^`), se antepone un punto para indicar la aplicación es elemento a elemento. Con funciones prefijo, como `sqrt` y `sin`, el punto se coloca después:
~~~~
julia> x .* y # multiplicación elemento a elemento
2-element Vector{Int64}:
3
8
julia> x .^ 2 # cuadrado elemento a elemento
2-element Vector{Int64}:
1
4
julia> sin.(x) # aplicación de sin elemento a elemento
2-element Vector{Float64}:
0.8414709848078965
0.9092974268256817
julia> sqrt.(x) # aplicación de sqrt elemento a elemento
2-element Vector{Float64}:
1.0
1.4142135623730951
~~~~
## Matrices
Una matriz es un conjunto bidimensional de valores. Al igual que un vector, se construye utilizando corchetes, y al igual que estos, son realmente un alias para un tipo particular de array. Utilizamos espacios para delimitar los elementos de una misma fila y punto y coma para delimitar las filas. También podemos indexar en la matriz y sacar submatrices utilizando rangos:
~~~~
julia> X = [1 2 3; 4 5 6; 7 8 9; 10 11 12];
julia> typeof(X) # una matriz bidimensional de Int64s
Matrix{Int64} (alias for Array{Int64, 2})
julia> X[2] # segundo elemento utilizando la ordenación columna-mayor
4
julia> X[3,2] # elemento en la tercera fila y la segunda columna
8
julia> X[1,:] # extrae la primera fila
3-element Vector{Int64}:
1
2
3
julia> X[:,2] # extrae la segunda columna
4-element Vector{Int64}:
2
5
8
11
julia> X[:,1:2] # extrae las dos primeras columnas
4×2 Matrix{Int64}:
1 2
4 5
7 8
10 11
julia> X[1:2,1:2] # extrae una submatriz de 2x2 de la parte superior izquierda de x
2×2 Matrix{Int64}:
1 2
4 5
julia> Matrix{Float64} # alias para una matriz bidimensional
Matrix{Float64} (alias for Array{Float64, 2})
~~~~
También podemos construir una variedad de matrices especiales y utilizar comprensiones de matrices:
~~~~
julia> Matrix(1.0I, 3, 3) # Matriz identidad 3x3
3×3 Matrix{Float64}:
1.0 0.0 0.0
0.0 1.0 0.0
0.0 0.0 1.0
julia> Matrix(Diagonal([3, 2, 1])) # Matriz diagonal 3x3 con 3, 2, 1 en la diagonal
3×3 Matrix{Int64}:
3 0 0
0 2 0
0 0 1
julia> zeros(3,2) # Matriz 3x2 de ceros
3×2 Matrix{Float64}:
0.0 0.0
0.0 0.0
0.0 0.0
julia> rand(3,2) # Matriz aleatoria 3x2
3×2 Matrix{Float64}:
0.694045 0.495397
0.761154 0.884542
0.342425 0.01093
julia> [sin(x + y) for x in 1:3, y in 1:2] # comprensión matricial
3×2 Matrix{Float64}:
0.909297 0.14112
0.14112 -0.756802
-0.756802 -0.958924
~~~~
Las operaciones de matrices incluyen las siguientes:
~~~~
julia> X' # transposición conjugada compleja
3×4 adjoint(::Matrix{Int64}) with eltype Int64:
1 4 7 10
2 5 8 11
3 6 9 12
julia> 3X .+ 2 # multiplicando por un escalar y sumando un escalar
4×3 Matrix{Int64}:
5 8 11
14 17 20
23 26 29
32 35 38
julia> X = [1 3; 3 1]; # crear una matriz invertible
julia> inv(X) # inversion
2×2 Matrix{Float64}:
-0.125 0.375
0.375 -0.125
julia> pinv(X) # pseudoinversa (requiere LinearAlgebra)
2×2 Matrix{Float64}:
-0.125 0.375
0.375 -0.125
julia> det(X) # determinante (requiere LinearAlgebra)
-8.0
julia> [X X] # concatenación horizontal, igual que hcat(X, X)
2×4 Matrix{Int64}:
1 3 1 3
3 1 3 1
julia> [X; X] # concatenación vertical, igual que vcat(X, X)
4×2 Matrix{Int64}:
1 3
3 1
1 3
3 1
julia> sin.(X) # aplicación de sin elemento a elemento
2×2 Matrix{Float64}:
0.841471 0.14112
0.14112 0.841471
julia> map(sin, X) # aplicación de sin elemento a elemento
2×2 Matrix{Float64}:
0.841471 0.14112
0.14112 0.841471
julia> vec(X) # reestructurar una matriz como un vector
4-element Vector{Int64}:
1
3
3
1
~~~~
## Tuplas
Una tupla es una lista ordenada de valores, potencialmente de diferentes tipos. Se construyen con paréntesis. Son similares a los vectores, pero no pueden ser mutados:
~~~~
julia> x = () # la tupla vacía
()
julia> isempty(x)
true
julia> x = (1,) # las tuplas de un elemento necesitan la coma final
(1,)
julia> typeof(x)
Tuple{Int64}
julia> x = (1, 0, [1, 2], 2.5029, 4.6692) # el tercer elemento es un vector
(1, 0, [1, 2], 2.5029, 4.6692)
julia> typeof(x)
Tuple{Int64, Int64, Vector{Int64}, Float64, Float64}
julia> x[2]
0
julia> x[end]
4.6692
julia> x[4:end]
(2.5029, 4.6692)
julia> length(x)
5
julia> x = (1, 2)
(1, 2)
julia> a, b = x;
julia> a
1
julia> b
2
~~~~
## Tuplas con nombre
Una tupla con nombre es como una tupla, pero cada entrada tiene su propio nombre:
~~~~
julia> x = (a=1, b=-Inf)
(a = 1, b = -Inf)
julia> x isa NamedTuple
true
julia> x.a
1
julia> a, b = x;
julia> a
1
julia> (; :a=>10)
(a = 10,)
julia> (; :a=>10, :b=>11)
(a = 10, b = 11)
julia> merge(x, (d=3, e=10))
# merge two named tuples
(a = 1, b = -Inf, d = 3, e = 10)
~~~~
## Diccionarios
Un diccionario es una colección de pares *clave-valor*. Los pares clave-valor se indican con un operador de doble flecha `=>`. Podemos indexar en un diccionario utilizando corchetes, al igual que con las matrices y las tuplas:
~~~~
julia> x = Dict(); # diccionario vacío
julia> x[3] = 4 # asociar la clave 3 con el valor 4
4
julia> x = Dict(3=>4, 5=>1) # crear un diccionario con dos pares clave-valor
Dict{Int64, Int64} with 2 entries:
5 => 1
3 => 4
julia> x[5] # devuelve el valor asociado a la clave 5
1
julia> haskey(x, 3) # comprueba si el diccionario tiene la clave 3
true
julia> haskey(x, 4) # comprueba si el diccionario tiene la clave 4
false
~~~~
## Tipos compuestos (estructuras)
Un tipo compuesto, o estructura, es una colección de campos con nombre. Por defecto, una instancia de un tipo compuesto es inmutable (es decir, no puede cambiar). Usamos la palabra clave `struct` y luego le damos un nombre al nuevo tipo y enumeramos los nombres de los campos:
~~~~
struct A
a
b
end
~~~~
Añadir la palabra clave `mutable` hace que una instancia pueda cambiar:
~~~~
mutable struct B
a
b
end
~~~~
Los tipos compuestos se construyen con paréntesis, entre los que se pasan valores para cada campo:
~~~~
x = A(1.414, 1.732)
~~~~
El operador de doble punto puede utilizarse para especificar el tipo de cualquier campo:
~~~~
struct A
a::Int64
b::Float64
end
~~~~
Estas anotaciones de tipo requieren que pasemos un `Int64` para el primer campo y un `Float64` para el segundo. Por razones de compacidad, no utilizaremos anotaciones de tipo, pero es a expensas del rendimiento. Las anotaciones de tipo permiten a Julia mejorar el rendimiento en tiempo de ejecución porque el compilador puede optimizar el código subyacente para tipos específicos.
## Tipos abstractos
Hasta ahora hemos discutido los tipos concretos, que son tipos que podemos construir. Sin embargo, los tipos concretos son sólo una parte de la jerarquía de tipos. También hay tipos abstractos, que son supertipos de tipos concretos y otros tipos abstractos.
Podemos explorar la jerarquía de tipos del tipo `Float64` mostrada en la figura siguiente utilizando las funciones de `supertype` y `subtype`:

~~~~
julia> supertype(Float64)
AbstractFloat
julia> supertype(AbstractFloat)
Real
julia> supertype(Real)
Number
julia> supertype(Number)
Any
julia> supertype(Any) # Any está en la cima de la jerarquía
Any
julia> using InteractiveUtils # necesario para utilizar subtipos en scripts
julia> subtypes(AbstractFloat) # diferentes tipos de AbstractFloats
4-element Vector{Any}:
BigFloat
Float16
Float32
Float64
julia> subtypes(Float64) # Float64 no tiene subtipos
Type[]
~~~~
Podemos definir nuestros propios tipos abstractos:
~~~~
abstract type C end
abstract type D <: C end # D es un subtipo abstracto de C
struct E <: D # E es un tipo compuesto que es un subtipo de D
a
end
~~~~
## Tipos paramétricos
Julia soporta tipos paramétricos, que son tipos que toman parámetros. Los parámetros de un tipo paramétrico se dan entre llaves y delimitados por comas. Ya hemos visto un tipo paramétrico con nuestro ejemplo del diccionario:
~~~~
julia> x = Dict(3=>1.4, 1=>5.9)
Dict{Int64, Float64} with 2 entries:
3 => 1.4
1 => 5.9
~~~~
Para los diccionarios, el primer parámetro especifica el tipo de clave, y el segundo parámetro especifica el tipo de valor. El ejemplo tiene claves `Int64` y valores `Float64`, haciendo que el diccionario sea del tipo `Dict{Int64,Float64}`. Julia fue capaz de inferir estos tipos en base a la entrada, pero podríamos haberlo especificado explícitamente:
~~~~
julia> x = Dict{Int64,Float64}(3=>1.4, 1=>5.9);
~~~~
Aunque es posible definir nuestros propios tipos paramétricos, nosotros no lo haremos.
# Funciones
Una función asigna sus argumentos, dados como una tupla, a un resultado que se devuelve.
## Funciones con nombre
Una forma de definir una función con nombre es utilizar la palabra clave `function`, seguida del nombre de la función y una tupla de nombres de argumentos:
~~~~
function f(x, y)
return x + y
end
~~~~
También podemos definir funciones de forma compacta utilizando la forma de asignación:
~~~~
julia> f(x, y) = x + y;
julia> f(3, 0.1415)
3.1415
~~~~
## Funciones anónimas
Una función anónima no recibe un nombre, aunque puede ser asignada a una variable con nombre. Una forma de definir una función anónima es utilizar el operador `->`:
~~~~
julia> h = x -> x^2 + 1 # asignar una función anónima con entrada x a una variable h
#1 (generic function with 1 method)
julia> h(3)
10
julia> g(f, a, b) = [f(a), f(b)]; # aplica la función f a a y b y devuelve el array
julia> g(h, 5, 10)
2-element Vector{Int64}:
26
101
julia> g(x->sin(x)+1, 10, 20)
2-element Vector{Float64}:
0.4559788891106302
1.9129452507276277
~~~~
## Objetos invocables
Podemos definir un tipo y asociar funciones a él, permitiendo que los objetos de ese tipo sean invocables:
~~~~
julia> (x::A)() = x.a + x.b # añadir una función de cero argumentos al tipo A definido anteriormente
julia> (x::A)(y) = y*x.a + x.b # añadir una función de un solo argumento
julia> x = A(22, 8);
julia> x()
30
julia> x(2)
52
~~~~
## Argumentos opcionales
Podemos asignar un valor por defecto a un argumento, haciendo que la especificación de ese argumento sea opcional:
~~~~
julia> f(x=10) = x^2;
julia> f()
100
julia> f(3)
9
julia> f(x, y, z=1) = x*y + z;
julia> f(1, 2, 3)
5
julia> f(1, 2)
3
~~~~
## Argumentos de palabra clave
Las funciones pueden utilizar argumentos de palabra clave, que son argumentos que se nombran cuando se llama a la función. Los argumentos de palabra clave se dan después de todos los argumentos posicionales. Se coloca un punto y coma antes de las palabras clave, separándolas de los demás argumentos:
~~~~
julia> f(; x = 0) = x + 1;
julia> f()
1
julia> f(x = 10)
11
julia> f(x, y = 10; z = 2) = (x + y)*z;
julia> f(1)
22
julia> f(2, z = 3)
36
julia> f(2, 3)
10
julia> f(2, 3, z = 1)
5
~~~~
## Dispatch
Los tipos de los argumentos pasados a una función pueden ser especificados usando el operador de dos puntos dobles. Si se proporcionan múltiples métodos de la misma función, Julia ejecutará el método apropiado. El mecanismo para elegir el método a ejecutar se llama _dispatch_:
~~~~
julia> f(x::Int64) = x + 10;
julia> f(x::Float64) = x + 3.1415;
julia> f(1)
11
julia> f(1.0)
4.141500000000001
julia> f(1.3)
4.4415000000000004
~~~~
Se utilizará el método con la signatura de tipo que mejor se ajuste a los tipos de los argumentos dados:
~~~~
julia> f(x) = 5;
julia> f(x::Float64) = 3.1415;
julia> f([3, 2, 1])
5
julia> f(0.00787499699)
3.1415
~~~~
## Splatting
A menudo es útil dividir los elementos de un vector o una tupla en los argumentos de una función utilizando el operador `...`:
~~~~
julia> f(x,y,z) = x + y - z;
julia> a = [3, 1, 2];
julia> f(a...)
2
julia> b = (2, 2, 0);
julia> f(b...)
4
julia> c = ([0,0],[1,1]);
julia> f([2,2], c...)
2-element Vector{Int64}:
1
1
~~~~
# Control de flujo
Podemos controlar el flujo de nuestros programas utilizando la evaluación condicional y los bucles.
## Evaluación condicional
La evaluación condicional comprobará el valor de una expresión booleana y luego evaluará el bloque de código apropiado. Una de las formas más comunes de hacer esto es con una sentencia `if`:
~~~~
if x < y
# ejecutar esto si x < y
elseif x > y
# ejecutar esto si x > y
else
# ejecutar esto si x == y
end
~~~~
También podemos utilizar el operador ternario con su sintaxis de signos de interrogación y dos puntos. Comprueba la expresión booleana antes del signo de interrogación. Si la expresión se evalúa como verdadera, entonces devuelve lo que viene antes de los dos puntos; de lo contrario, devuelve lo que viene después de los dos puntos:
~~~~
julia> f(x) = x > 0 ? x : 0;
julia> f(-10)
0
julia> f(10)
10
~~~~
## Bucles
Un bucle permite la evaluación repetida de expresiones. Un tipo de bucle es el bucle `while`, que evalúa repetidamente un bloque de expresiones hasta que se cumpla la condición especificada tras la palabra clave `while`. El siguiente ejemplo suma los valores del array `x`:
~~~~
X = [1, 2, 3, 4, 6, 8, 11, 13, 16, 18]
s = 0
while !isempty(X)
s += pop!(X)
end
~~~~
Otro tipo de bucle es el bucle `for`, que utiliza la palabra clave `for`. El siguiente ejemplo también sumará los valores del array `x` pero no modificará `x`:
~~~~
X = [1, 2, 3, 4, 6, 8, 11, 13, 16, 18]
s = 0
for y in X
s += y
end
~~~~
La palabra clave `in` puede sustituirse por `=` o `∈`. El siguiente bloque de código es equivalente:
~~~~
X = [1, 2, 3, 4, 6, 8, 11, 13, 16, 18]
s = 0
for i = 1:length(X)
s += X[i]
end
~~~~
## Iteradores
Podemos iterar sobre colecciones en contextos como los bucles `for` y las comprensiones de arrays. Para demostrar varios iteradores, utilizaremos la función `collect`, que devuelve un array de todos los elementos generados por un iterador:
~~~~
julia> X = ["feed", "sing", "ignore"];
julia> collect(enumerate(X)) # devuelve el recuento y el elemento
3-element Vector{Tuple{Int64, String}}:
(1, "feed")
(2, "sing")
(3, "ignore")
julia> collect(eachindex(X)) # equivalente a 1:length(X)
3-element Vector{Int64}:
1
2
3
julia> Y = [-5, -0.5, 0];
julia> collect(zip(X, Y)) # iterar sobre múltiples iteradores simultáneamente
3-element Vector{Tuple{String, Float64}}:
("feed", -5.0)
("sing", -0.5)
("ignore", 0.0)
julia> import IterTools: subsets
julia> collect(subsets(X)) # iterar sobre todos los subconjuntos
8-element Vector{Vector{String}}:
[]
["feed"]
["sing"]
["feed", "sing"]
["ignore"]
["feed", "ignore"]
["sing", "ignore"]
["feed", "sing", "ignore"]
julia> collect(eachindex(X)) # iterar sobre los índices de una colección
3-element Vector{Int64}:
1
2
3
julia> Z = [1 2; 3 4; 5 6];
julia> import Base.Iterators: product
julia> collect(product(X,Y)) # iterar sobre el producto cartesiano de múltiples iteradores
3×3 Matrix{Tuple{String, Float64}}:
("feed", -5.0) ("feed", -0.5) ("feed", 0.0)
("sing", -5.0) ("sing", -0.5) ("sing", 0.0)
("ignore", -5.0) ("ignore", -0.5) ("ignore", 0.0)
~~~~
# Salidas
## Salida a ficheros
Una opción para una salida diferente es enviar las salidas a un archivo separado en lugar de a la consola. Esto se hace en tres pasos:
1. Abrir un archivo en el que se pueda escribir (denotado por el parámetro `"w"`) como variable (para poder referenciarlo posteriormente). El nombre de archivo dado representa una ruta relativa a la carpeta actual, que puede verse mediante `pwd()`. Si no existe ningún fichero con esta ruta, se creará uno:
```
textfile = open("text.txt", "w")
```
2. Escribir en el fichero, utilizando funciones como `show` o `println` en combinación con el fichero como parámetro. Por ejemplo, el vector `a = [1, 2, 3, 4]` puede escribirse en el fichero mediante:
```
println(textfile, a)
```
3. Cierra el fichero para grabarlo:
```
close(textfile)
```
Si todos los datos que deben escribirse en el fichero están listos, pueden combinarse en una única sentencia, de la forma:
```
open("text.txt", "w") do textfile
println(textfile, a)
end
```
que cerrará automáticamente el archivo una vez finalizada la sentencia `do`.
## Tablas
Una tabla es a menudo la mejor manera de presentar los datos, por lo que tener una forma de crearlas automáticamente es muy útil. Contrariamente a lo esperado, el paquete `Tables` no es el paquete adecuado para hacer esto, ya que es más útil para la manipulación de tablas como base de datos que para mostrarlas como objetos. Para este propósito, una buena opción es `PrettyTables`.
```
using PrettyTables
```
En su uso más básico, `PrettyTables` permite convertir una matriz en una tabla:
```julia
M =
4×4 Matrix{Float64}:
0.437554 0.269954 0.671587 0.955436
0.0488504 0.498904 0.323736 0.893687
0.46298 0.877554 0.111193 0.603234
0.155545 0.106083 0.594877 0.723867
M = rand(4,4)
```
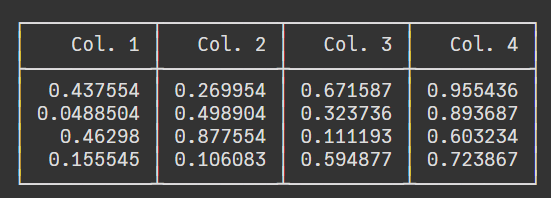
```julia
with_terminal() do
pretty_table(M)
end
```
Una cosa importante con PrettyTables es que las tablas obtenidas se imprimen en la REPL (u otra salida de su elección), y no se devuelven como variables. Como resultado, para propósitos de visualización dentro de un notebook de Pluto, las tablas tendrán que ser devueltas en mini-terminales como arriba, creadas por la función `with_terminal`. Desafortunadamente, las limitaciones de estos terminales significan que muchas características de PrettyTables no pueden ser visualizadas directamente desde un notebook. Para utilizar este código en la REPL, basta copiar sólo el contenido del bloque `do` (en el ejemplo anterior, `pretty_table(M)`).
El poder de `PrettyTables` reside en la multitud de personalizaciones que se pueden hacer a la tabla. Éstas, y el paquete en su conjunto, están ampliamente documentadas [aquí](https://ronisbr.github.io/PrettyTables.jl/stable/).
La palabra clave más importante es `backend`, que permite elegir entre tres formas de salida para la tabla (y la mayoría de las otras palabras clave dependen de qué backend se elija):
* `backend = :text` es el valor por defecto, la salida de la tabla en texto sin formato.
* `backend = :html` genera una salida HTML que define la tabla.
* `backend = :latex` genera el código LaTeX que define la tabla como un objeto tabular.
Además, las salidas se pueden escribir en archivos de la misma manera que `show` o `println` pueden tener su salida escrita en archivos:
```
open("tablefile.txt", "w") do io
pretty_table(io, M; header = ["Player $i" for i = 1:4])
end
```
## Gráficas
Resumen de Makie... por hacer.
# Paquetes
Un paquete es una colección de código de Julia y posiblemente otras bibliotecas externas que pueden ser importadas para proporcionar funcionalidad adicional. Esta sección revisa brevemente algunos de los paquetes clave en los que nos basaremos para el curso. Para añadir un paquete registrado como `Graphs.jl`, podemos ejecutar
~~~~
using Pkg
Pkg.add("Graphs")
~~~~
Para actualizar los paquetes, utilizamos
~~~~
Pkg.update()
~~~~
Alternativamente, podemos entrar en el entorno que el gestor de paquetes nos ofrece desde dentro de Julia, para ello:
````
julia> ]
(@v1.9) pkg>
(@v1.9) pkg> add Graphs
....
(@v1.9) pkg>
````
Aunque todo lo anterior es ligeramente distinto si usamos el entorno Pluto.jl para trabajar (como será nuestro caso). Puedes encontrar algo más de información acerca de cómo funciona en el documento de instalación de Julia.
Para utilizar un paquete, utilizamos la palabra clave `using` de la siguiente manera:
~~~~
using Graphs
~~~~
A lo largo del curso haremos uso de diversos paquetes que facilitan diversas tareas, y que detallaremos en el momento adecuado, por ejemplo: `Graphs.jl` (para representar grafos y realizar operaciones con ellos), `JuMP.jl` (para especificar problemas de optimización que luego podemos resolver utilizando una variedad de solucionadores), `Makie.jl` (para visualizaciones gráficas), etc.