**LITI** Formas Normales, Cláusulas y Algoritmo DPLL En el tema anterior estudiamos un método, el de _Tableros Semánticos_, basado en el manejo y transformación de los conjuntos de fórmulas en otros equivalentes más sencillos, tanto en LP como en LPO, para tratar de resolver el problema de la satisfactibilidad de conjuntos de fórmulas. Una de las características que destacábamos de los Tableros Semánticos es que no necesitaban de ningún tipo de preprocesamiento en las fórmulas para poder ser aplicados. Sin embargo, al igual que en muchos otros métodos de procesamiento de muchas áreas, suele ser más habitual encontrar algoritmos de procesamiento de fórmulas que necesitan que éstas tengan una estructura determinada, pasando por una etapa de preprocesamiento. En este tema vamos a abordar los métodos más comunes de preprocesamiento de fórmulas LP, que también serán aplicables a fórmulas LPO, y mostraremos uno de los algoritmos centrales para $SAT$ que hace uso de este preprocesamiento, $DPLL$, en el que se basan la gran mayoría de métodos actuales que abordan ese problema. # Introducción En el tema anterior ya hicimos un uso implícito del concepto de **equivalencia** entre fórmulas, sin embargo no dimos una definición formal de cuando dos fórmulas son equivalentes: !!!def:Equivalencia Dos fórmulas $F, G \in PROP$ son equivalentes, y se denota por $F \equiv G$ si y sólo si para toda valoración $v$ se tiene que $v(F)=v(G)$. !!!note De forma que son equivalentes a lo anterior: * $F$ y $G$ poseen, exactamente, los mismos modelos. * $F \equiv G$ si y sólo si $F \models G$ y $G \models F$ * $F \leftrightarrow G$ es lógicamente válida. Aunque hay infinidad de equivalencias entre fórmulas existen algunas, definidas de manera general, que forman parte de las conocidas como _reglas algebraicas LP_ o **reglas del álgebra proposicional**. Entre ellas destacamos: | Nombre | Equivalencia | |--------------------------|-------------------------------------------------------------------------------------------------------| | Conmutativa | $A \vee B \equiv B \vee A$
$A \wedge B \equiv B \wedge A$ | | Asociativa | $A\vee(B\vee C)\equiv (A\vee B)\vee C$
$A\wedge (B\wedge C)\equiv (A\wedge B)\wedge C$ | | Distributiva | $A\wedge (B\vee C)\equiv (A\wedge B)\vee (A\wedge C)$
$A\vee(B\wedge C)\equiv(A\vee B)\wedge(A\vee C)$ | | Doble Negación | $\neg \neg A\equiv A$ | | De Morgan | $\neg(A\vee B)\equiv \neg A\wedge \neg B$
$\neg(A\wedge B)\equiv \neg A\vee \neg B$ | | Idempotencia | $A\wedge A\equiv A$
$A\vee A\equiv A$ | | Absorción | $A\vee(A\wedge B)\equiv A$
$A\wedge (A\vee B)\equiv A$ | | de Tautología | $A\in TAU\Rightarrow (A\vee B)\equiv A$
$A\in TAU\Rightarrow (A\wedge B)\equiv B$ | | de Inconsistencia | $A\notin SAT\Rightarrow (A\vee B)\equiv B$
$A\notin SAT\Rightarrow (A\wedge B)\equiv A$ | | Implicación | $A\rightarrow B\equiv \neg A\vee B$ | | Doble Implicación | $A\leftrightarrow B \equiv (A\rightarrow B)\wedge (B\rightarrow A)$ | La aplicación de estas leyes, que son fácilmente verificables por medio de tablas de verdad, nos proporciona un método de **transformación por equivalencias** de fórmulas proposicionales gracias al concepto de sustitución: !!!Def: Sustitución Dadas $A, A', B \in PROP$, la **sustitución** de $A$ por $A'$ en $B$, denotada por $B_{\{A/A'\} }$, corresponde a la fórmula que resulta de intercambiar toda aparición de $A$ en $B$ por $A'$. Por ejemplo: !!!Tip $$ \begin{array}{ccc} B & \qquad & B_{\{A/A'\} } \\ \overbrace{p\to \underbrace{\color{red}{(q\land r)} }_A \lor \lnot s}& & \overbrace{p\to \underbrace{\color{blue}{(t\to \lnot r)} }_{A'}\lor \lnot s}\\ \end{array} $$ Y podemos obtener fácilmente el conocido como **Teorema de Sustitución**: !!!note: Teorema de Sustitución Si $A, A', B \in PROP$ $A \equiv A'$, entonces $B_{\{A/A'\} } \equiv B$. Por ejemplo: !!!Tip $$ \begin{array}{lcl} B\lor (A\land (A\rightarrow B)) & \equiv & B\lor (A\land (\lnot A\lor B)) \\ & \equiv & B\lor (A\land \lnot A)\lor (A \land B) \\ &\equiv & B\lor (A\land B)\equiv B \\ \end{array} $$ Lo que nos permite diseñar procedimientos de obtención de fórmulas equivalentes como veremos en la sección siguiente. # Formas Normales Conjuntiva, Disyuntiva y Clausal ## Literales proposicionales !!!Def:Literales Una fórmula $F \in PROP$ es un **literal** si corresponde a una variable proposicional o la negación de una variable proposicional. Es decir, $Lit=VP\cup \{\neg p:\ p\in VP\}$. Además se dice que dos literales son **complementarios** si uno corresponde a la negación del otro, y se denota por $L^{c}$ (por ejemplo, $p^c = \neg p$, y $(\neg p)^c =p$). Cuando tenemos fórmulas construidas de forma sencilla a partir de literales, resulta sencillo reducir la satisfactibilidad y validez de un conjunto de literales: !!!note:Lema Sea $\Sigma = \{L_1, \ldots, L_n\}$ un conjunto de literales. Entonces: 1. $\bigvee \limits_{i=1 \ldots n} L_i \in TAUT \Leftrightarrow \Sigma$ contiene un p par de literales complementarios. 2. $\bigwedge \limits_{i=1 \ldots n} L_i \not \in SAT \Leftrightarrow \Sigma$ contiene un par de literales complementarios. ## Formas normales El lema anterior da lugar a poder expresar una fórmula de dos formas alternativas, que permiten resolver su satisfactibilidad de forma más sencilla: !!!Def Una fórmula está en **Forma Normal Conjuntiva (FNC)** si corresponde a una conjunción de disyunciones de literales, es decir: $$F = \bigwedge \limits_{i=1}^{n}\left(\bigvee \limits_{j=1}^{m_i} L_{i,j}\right)$$ Una fórmula está en **Forma Normal Disyuntiva (FNC)** si corresponde a una disyunción de conjunción de literales, es decir: $$F = \bigvee \limits_{i=1}^{n}\left(\bigwedge \limits_{j=1}^{m_i} L_{i,j}\right)$$ Como muestra el resultado siguiente, es fácil determinar la satisfactibilad y tautología de fórmulas que vienen expresadas en estas formas: !!!note:Corolario 1. Una fórmula expresada en FNC es una tautología si y sólo si cada una de sus disyunciones es una tautología. 2. Una fórmula expresada en FND es insatisfactible si y sólo si cada una de sus conjunciones es insatisfactible. Un resultado así no es muy útil si no tenemos la fórmula expresada en uno de esos dos formatos, pero el siguiente resultado nos confirma que, realmente, el resultado es generalizable a todas las fórmulas proposicionales gracias a las transformaciones por equivalencia:: !!!note:Teorema Para toda fórmula $F \in PROP$: 1. Existe $F_1 \in PROP$ expresada en $FNC$ tal que $F \equiv F_1$. 2. Existe $F_2 \in PROP$ expresada en $FND$ tal que $F \equiv F_2$. De esta forma, transformar las fórmulas a FNC y FND se convierte en una tarea fundamental para la determinación de su satisfactibilidad/validez, por lo que se convierte en un preprocesamiento necesario para muchos algoritmos de decisión. Además el proceso de transformación es totalmente sistemático sin más que seguir los siguientes pasos: 1. Eliminación de las equivalencias, siguiendo la regla: $$ A \leftrightarrow B \equiv (A \rightarrow B) \wedge (B \rightarrow A)$$ 2. Eliminación de las implicaciones, siguiendo la regla: $$ A \rightarrow B \equiv \neg A \vee B $$ 3. Interiorizar las negaciones, aplicando las leyes de De Morgan: $$ \begin{array}{c} \neg (A \vee B) \equiv \neg A \wedge \neg B \\ \neg (A \wedge B) \equiv \neg A \vee \neg B \end{array}$$ 4. Eliminación de las dobles negaciones, siguiendo la ley de la Doble Negación: $$\neg \neg A \equiv A$$ Los pasos anteriores dan lugar a los que se conoce como **Forma Normal Negativa** (NNF), que es el germen de la que se puede obtener una $FNC$ o una $FND$ según se aplique una u otra ley distributiva: * Pasar a FND: aplicando la primera ley distributiva: $$A \wedge (B \vee C) \equiv (A \wedge B) \vee (A \wedge C)$$ * Pasar a FNC: aplicando la segunda ley distributiva: $$A \vee (B \wedge C) \equiv (A \vee B) \wedge (A \vee C)$$ Por ejemplo: !!!Tip Obtener una FNC de $(\lnot p\land q) \rightarrow(q\lor r)\rightarrow p$: $$ \begin{array}{lcl} (\lnot p\land q) \rightarrow (q\lor r)\rightarrow p &\Rightarrow &\\ &\Rightarrow& \lnot(\lnot p \land q) \lor ((q\lor r) \rightarrow p)\\ &\Rightarrow& \lnot(\lnot p \land q) \lor \lnot (q\lor r) \lor p \\ &\Rightarrow&\lnot \lnot p \lor \lnot q \lor (\lnot q\land \lnot r) \lor p\\ &\Rightarrow& p \lor \lnot q \lor ((\lnot q\lor p) \land (\lnot r \lor p))\\ &\Rightarrow& ( p \lor \lnot q \lor \lnot q \lor p) \land ( p \lor \lnot q \lor \lnot r \lor p)\\ &\Rightarrow& (\lnot q \lor p) \land (\lnot q \lor \lnot r \lor p) \\ \end{array} $$ De forma que ahora resulta directo reducir los problemas básicos (debido a las características que presentan, cada forma normal se usará preferentemente para resolver el problema más adecuado): * Satisfactibilidad: **Procedimiento FND**:  * Validez (Tautología): **Procedimiento FNC**:  ## Tableros Completos y Formas Normales En el tema anterior vimos el uso de los Tableros Semánticos como algoritmo de decisión y como algoritmo de búsqueda de modelos. A partir de los modelos de una fórmula se puede reconstruir una fórmula equivalente que está en $FND$: * De cada hoja abierta se toma la conjunción de literales que aparecen en ella. * Se hace la disyunción de todas las conjunciones anteriores. Por ejemplo: si $F$ es la fórmula $q\land s\land (q\rightarrow (r\rightarrow \neg p))$, entonces:  Por lo que una $FND$ de $F$ sería: $(q\land s\land \neg r)\lor (q\land s\land \neg p)$. Además, mediante la aplicación de las Leyes de De Morgan y la Ley de la Doble Negación, es fácil comprobar que la negación de una $FND$ resulta ser una $FNC$ (y viceversa), por tanto, también podemos calcular la $FNC$ de una fórmula proposicional, $F \in PROP$, a partir de un tablero semántico adecuado: * Se toma la fórmula $\neg F$ y se construye un Tablero Semántico completo. * Se construye la $FND$ de $\neg F$ a partir de este tablero. * Se obtiene la $FNC$ de $F$ negando la $FND$ anterior: $FNC(F) \equiv \neg FND(\neg F)$. Los dos últimos pasos se pueden reducir en uno y obtener $FNC(F)$ directamente tomando la conjunción de las hojas abiertas del tablero construido para $\neg F$, pero con la precaución de tomar en cada una de ellas la disyunción de los literales complementarios que aparecen en ella. Por ejemplo, si $F$ es la fórmula $s\land ((r\rightarrow p)\rightarrow q)$, para calcula una $FNC$ suya, calculamos un tablero completo para $\neg F$:  Y, por tanto, una $FNC$ de $F$ sería: $s\land (\neg r \lor q)\land (\neg p\lor q)$. ## Forma Clausal Veremos que, realmente, la mayoría de los métodos que veremos a partir de ahora se centran mucho más en la $FNC$ que en la $FND$, y será nuestro preprocesamiento prioritario. Además, desde el punto de vista histórico fue así, y se desarrolló toda una metodología basada en considerar las disyunciones de literales como el elemento básico de razonamiento. En este sentido, nosotros usaremos también algunas definiciones provenientes de esa línea de trabajo, que no son más que una forma distinta de llamar y representar los mismos elementos que provienen de la $FNC$: !!!Def Una **cláusula** corresponde a una disyunción de literales $L_1, \vee \ldots \vee L_n$y se representa por $\{L_1, \ldots, L_n\}$. La representación en forma de conjunto tiene sentido ya que en la disyunción de literales el orden en que éstos vienen no es determinante (debido a las propiedades asociativas y conmutativas de la disyunción). Las cláusulas son suficientemente sencillas como para que la satisfactibilidad de un modelo se pueda comprobar de forma directa: !!!Def Dada una valoración, $v$, y una cláusula, $\{L_1, \ldots, L_n\}$, se tiene que $v \models \{L_1, \ldots, L_n\}$ si y solo si existe un literal, $L_i$ ($i=1, \ldots, n$), tal que $v \models L_i$ (es decir, $v(L_i)=1$). Así pues, si en una cláusula aparecen un par de literales complementarios a la vez, entonces esa cláusula no podrá tener ningún modelo (como fórmula, será insatisfactible), y en caso contrario será satisfactible (y es directo conocer sus modelos). Usando la notación conjuntista de las cláusulas (como conjuntos de literales) podríamos considerar el caso extremo en el que la cláusula sea el conjunto vacío (no tiene literales), que se denomina **cláusula vacía** y se representa por $\square$. Por convenio (motivados por el hecho de que para ninguna valoración podemos encontrar un literal de la cláusula vacía que la satisfaga) diremos que representa a una fórmula insatisfactible (contradicción). Si tenemos en cuenta que las cláusulas son solo una forma distinta (que veremos que es muy cómoda) de llamar y representar las disyunciones de literales, tenemos que: !!!Def Para toda fórmula $F \in PROP$ existe un conjunto de cláusulas $\{C_1, \ldots, C_n\}$ que resulta equivalente a dicha fórmula. Formalmente: $$ v \models F \Leftrightarrow v \models \{C_1, \ldots, C_n\}$$. Se dice que $\{C_1, \ldots, C_n\}$ corresponde a la **forma clausal** de $F$. Este resultado se deriva directamente de la existencia de una $FNC$ para $F$: ya que para $F$ existe una fórmula $FNC$ equivalente, $(L_{1,1} \vee L_{1,2} \vee \ldots \vee L_{1,m_1}) \wedge \ldots \wedge (L_{n,1} \vee L_{n,2} \vee \ldots \vee L_{n,m_n})$, basta tomar la forma clausal $\{C_1, \ldots, C_n\}$, donde $C_i\equiv \{L_{i,1}, \ldots, L_{i, m_i}\}$. Denotaremos por $FC(F)$ a una forma clausal para $F$. De nuevo, el orden de aparición de las cláusulas no importa, ya que la conjunción también verifica las propiedades conmutativa y asociativa. De ahí su representación como conjunto. Y su utilidad podemos extenderla de fórmulas individuales a conjuntos de fórmulas, ya que la satisfactibilidad del conjunto corresponde con la satisfactibilidad simultánea (o lo que es lo mismo, la satisfactibilidad de la conjunción) de todas sus fórmulas: !!!Def Para todo conjunto de fórmulas $\Sigma$ existe un conjunto de cláusulas $\{C_1, \ldots, C_n\}$ tal que: $$ v \models \Sigma \Leftrightarrow v \models \{C_1, \ldots, C_n\}$$ En otras palabras, el cálculo de los modelos de un conjunto de fórmulas se puede reducir al cálculo de modelos de un conjunto de cláusulas. Ya que se puede obtener una Forma Clausal para $\Sigma$ como: $FC(\Sigma)=\bigcup \limits_{F\in \Sigma} FC(F)$. Por ejemplo, si $U$ viene dada por: $$U=\{\underbrace{p\to q}_\mathbf{(1)},\, \underbrace{(p\lor \lnot q)\land (r\to \lnot p)}_\mathbf{(2)},\, \underbrace{p\land \lnot r}_\mathbf{(3)}\}$$ Una forma clausal de $U$ es: $$\{\underbrace{\lnot p\lor q}_\mathbf{(1)},\, \underbrace{p\lor \lnot q,\, \lnot r\lor \lnot p}_\mathbf{(2)},\,\underbrace{p,\, \lnot r}_\mathbf{(3)}\}$$ # Algoritmo DPLL El **algoritmo DPLL** es un algoritmo completo empleado como método de decisión para la satisfactibilidad de un conjunto de cláusulas (o, como hemos visto que son equivalentes, de fórmulas en $FNC$, por lo que se puede utilizar como algoritmo de decisión para cualquier conjunto de fórmulas si se aplica previamente una fase de preprocesamiento que construya una forma clausal para el conjunto). Su nombre proviene de los investigadores que trabajaron en su diseño en diversas aproximaciones: Davis, Putnam, Logemann, y Loveland. Fue presentado por Davis y Putnam en 1960 y refinado posteriormente, en 1962, por Davis, Logemann y Loveland. Proporciona un procedimiento muy eficiente y tras más de 40 años aún conforma la base de los resolvedores de SAT más exitosos (los _SAT Solvers_ son programas para determinar la satisfactibilidad de un conjunto de fórmulas proposicionales, habitualmente en forma clausal). Al igual que sucedía con los Tableros Semánticos, además de como algoritmo de decisión para SAT, DPLL proporciona también un método constructor de modelos. El algoritmo se basa en un método de construcción binaria realizando una búsqueda sistemática a través de los posibles valores que pueden tomar las variables proposicionales, de manera que en el peor de los casos, la complejidad del algoritmo resulta exponencial (no podemos esperar nada mejor, teniendo en cuenta que $SAT$ es **NP**\-completo). A pesar de que el proceso de búsqueda es habitualmente representado mediante un árbol binario, de forma similar a como lo hacíamos trabajando con Tableros Semánticos, existen claras diferencias entre ambos métodos: 1. DPLL: * No trabaja sobre los conjuntos de fórmulas _en bruto_, sino que es necesario realizar un preprocesamiento de los mismos para expresarlos como conjuntos clausales. * Resulta uno de los algoritmos más eficientes para la decisión de la satisfactibilad, pero su uso se restringe únicamente a LP. 2. Tableros Semánticos: * Trabaja sobre los conjuntos de fórmulas _en bruto_, esto es, sobre las fórmulas proposicionales sin tratamiento previo. * No resulta tan eficiente como DPLL pero la versatilidad del método permite adaptarlo a otras lógicas (LPO, descriptivas, modales, ...) donde resulta muy útil en el estudio teórico. En la actualidad existen muchas variantes de DPLL que añaden heurísticas y otras metodologías avanzadas para seleccionar los pasos sucesivos y acelerar la búsqueda de una solución. ## Estructura del algoritmo DPLL Podemos distinguir dos operaciones principales en el algoritmo: 1. **Propagación de unidades**, que tiene como objetivo simplificar el conjunto de cláusulas mediante la eliminación de cláusulas y literales. 2. **División**, que organiza la búsqueda de un modelo cuando no se puede simplificar por el paso anterior. El algoritmo puede describirse recursivamente como muestra el siguiente código:  Donde, en cada paso, las diversas fases que lo componen serían: ### Fase de Propagación de unidades Se elige una cláusula unitaria, esto es, que contenga un único literal, $L$, y se aplican consecutivamente las dos reglas siguientes: 1. **Subsunción Unitaria**. Se eliminan de $S$ todas las cláusulas subsumidas por $L$, es decir, aquellas que contengan $L$. Justificación: si $\{L\}$ es una cláusula de $S$, un modelo de $S$ debe hacer $v(L)=1$, por tanto, la cláusulas (que son disyunciones de literales) que contienen $L$ son ciertas automáticamente, y no nos permiten extraer más información del resto de literales, por lo que podemos eliminarlas del proceso de razonamiento. 2. **Resolución Unidad**. Se elimina el literal complementario, $L^{c}$, de todas las cláusulas de $S$ donde aparezca. Justificación: si $\{L\}$ es una cláusula de $S$, un modelo de $S$ debe hacer $v(L^c)=0$, por tanto, las cláusulas que contienen $L^c$ deben ser ciertas por el resto de literales que aparecen. En este caso, la aparición de $L^C$ sí informa acerca de la veracidad del resto de literales: $L_{1} \vee \ldots \vee L_{k} \vee L^c \equiv L_{1} \vee \ldots \vee L_{k}$. Este paso se realiza sucesivamente hasta que no quedan cláusulas unitarias en el conjunto:  ### Fase de División Si tras el proceso de propagación de unidades aún quedan cláusulas en el conjunto (ninguna será unitaria), se toma un literal $L$ que aparezca en alguna de las cláusulas de $S$ y se construyen dos nuevos conjuntos: $S'= S \cup \{L\}$ y $S''= S \cup \{L^{c}\}$. Es claro que la consistencia de $S$ se reduce a la consistencia de alguno de estos conjuntos. Por lo que el problema se divide en 2 problemas en los que ya hay cláusulas unitarias con las que podemos aplicar la fase anterior: $$S \text{ consistente} \Leftrightarrow (S' \text{ consistente}) \vee (S'' \text{ consistente})$$ Como las cláusulas unitarias fijan el valor de las variables proposicionales, cuando no tenemos ninguna hemos de asumir el valor de una de ellas para poder seguir, de forma que proporcionamos un método completo.  ## DPLL como resolvedor SAT y como Generador de modelos. Como hemos visto, DPLL tiene 2 condiciones de parada: 1. El conjunto de cláusulas a satisfacer es vacío, por lo que se ha alcanzado la satisfactibilidad del conjunto: > la rama proporciona un modelo a partir de las valoraciones que se han fijado para cada una de las variables proposicionales que han actuado como cláusulas unitarias en esa rama (positivas si aparece el literal positivo, negativas si aparece el literal negativo, e indeterminado si no aparecen). Además, las bifurcaciones en DPLL se producen cuando no hay cláusulas unitarias, y en ese caso el problema se divide en dos problemas nuevos que asignan a un literal las dos alternativas complementarias. Por tanto, las dos ramas distintas han de dar, necesariamente, modelos distintos, por lo que sabemos que en DPLL cada rama distinta proporciona modelos distintos (algo que no ocurría en el método de Tableros Semánticos). 2. Alguna de las cláusulas queda vacía, $\square$, por lo que el conjunto de fórmulas derivado en esa rama tiene una cláusula que no es satisfactible y dicha rama no proporciona ningún modelo (la rama se considera cerrada). # Ejemplos !!!Tip:Ejemplo 1 Por ejemplo, si $S=\{\{p,q,r\}, \{\lnot p,q,r\}, \{\lnot q,\, r\}, \{\lnot q,\,\lnot r\}, \{q,\,\lnot r\}\}$, ya dada en forma clausal, entonces:  Por lo que, como todas las ramas salen cerradas, con la cláusula vacía, el conjunto $S$ es insatisfactible. !!!Tip:Ejemplo 2 Si $S=\{\{p,q,r\}, \{\neg p,q,r\},\{p,\neg q\},\{p,r\},\{\neg p,\neg q,r\},\{\neg q,q,\neg r\},\{\neg p,\neg q,\neg r\}\}$  Por lo que $S$ es satisfactible, y un modelo suyo sería $v(p)=0$, $v(q)=0$ y $v(r)=1$ (de la aplicación de cláusulas unitarias de la rama abierta). 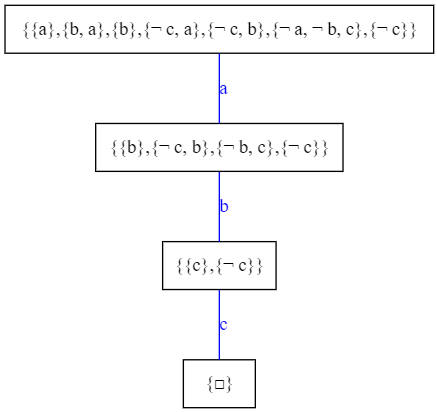!!!Tip:Ejemplo 3 $S=\{\{a\},\{b,a\},\{b\},\{\neg c,a\},\{\neg c,b\},\{\neg a,\neg b,c\},\{\neg c\}\}$  Por lo que $S$ es inconsistente. 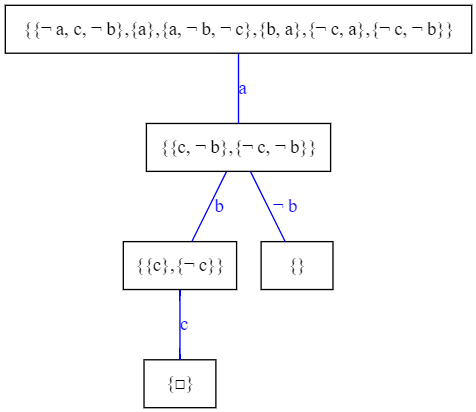!!!Tip:Ejercicio 4 $S=\{\{\neg a,c,\neg b\},\{a\},\{a,\neg b,\neg c\},\{b,a\},\{\neg c,a\},\{\neg c,\neg b\}\}$  Por lo que $S$ es consistente y sus modelos son: $\{a=1,b=0,c=0\}$ y $\{a=1, b=0,c=1\}$. 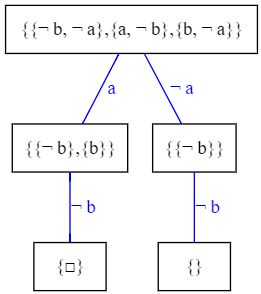!!!Tip:Ejemplo 5 $S=\{\{\neg b,\neg a\},\{a,\neg b\},\{b,\neg a\}\}$  Por lo que $S$ es consistente y tiene el modelo $\{a=0,b=0\}$. !!!Tip:Ejercicio 6 Consideremos el conjunto de fórmulas $U=\{r\leftrightarrow (p\lor q),\, s\rightarrow p,\,(\lnot s\land \lnot r)\rightarrow (s\lor t)\}.$ 1. Obtener una forma clausal de $U$. 2. Pruébese utilizando el algoritmo DPLL que $U\not\models p$. ¿Qué modelo proporciona el algoritmo? 3. Pruébese, mediante DPLL, que $U\models \lnot p\rightarrow (q\lor t)$. Solución: 1. El primer paso es pasar todas las fórmulas a forma clausal, o lo que es lo mismo, $FNC$. 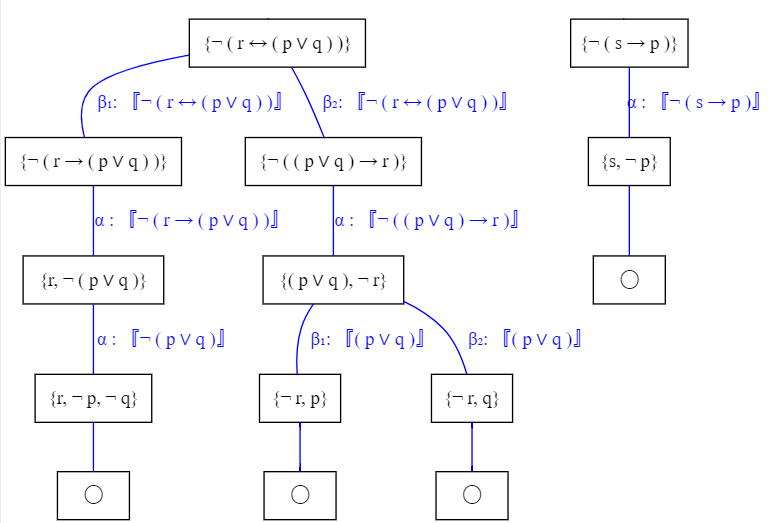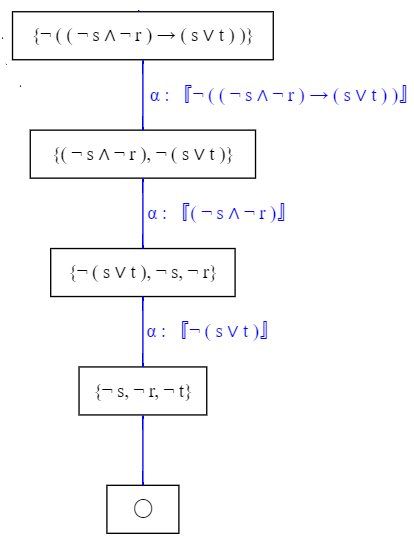Para ello, haremos uso de tableros semánticos transformando a $FND$ las negaciones de cada fórmula:   Por lo que la forma clausal de $U$ queda: $\{\{\neg r,p,q\},\{r,\neg p\},\{r,\neg q\},\{\neg s,p\},\{s,r,t\}\}$. 2. Para comprobar si $U\models p$ hemos de transformar el problema de la consecuencia en un problema de satisfactibilidad, que es lo que puede resolver DPLL, y lo hacemos por el Teorema de la Consecuencia visto en temas anteriores: $$U\models p \Leftrightarrow U\cup \{\neg p\} \text{ insatisfactible}$$ Lo que significa que el árbol de DPLL debería salir con todas sus ramas cerradas (con contradicciones):  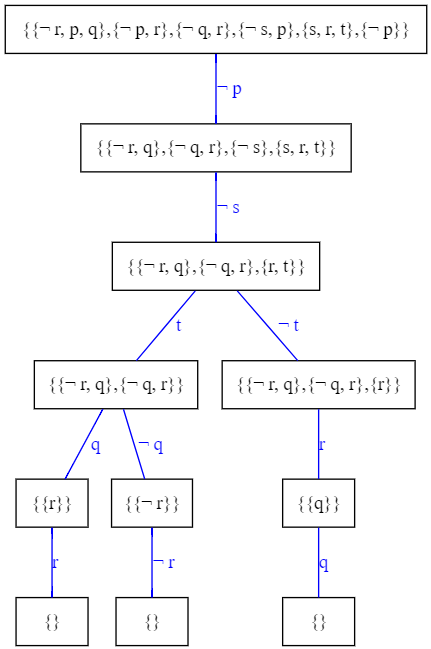Vemos que no es así, y que tiene ramas abiertas, por lo que el conjunto de cláusulas considerado es satisfactible y por tanto: $U\not\models p$. 3. 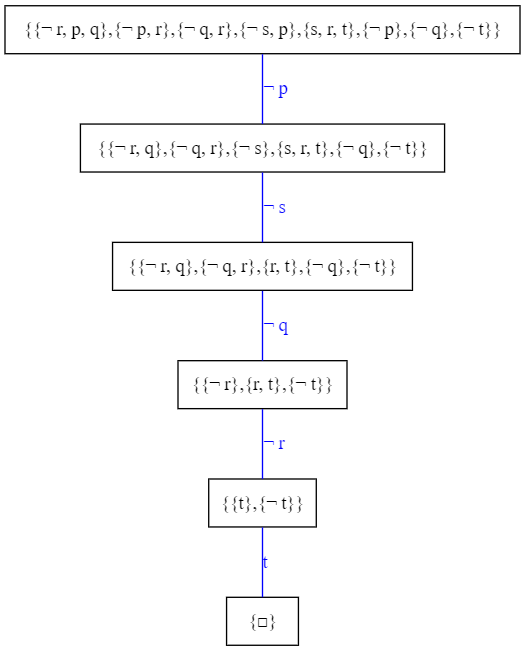Por un razonamiento análogo al anterior, $U\models \lnot p\rightarrow (q\lor t) \Leftrightarrow U\cup \{\neg (\lnot p\rightarrow (q\lor t))\}$ es insatisfactible, lo que se traduce en que DPLL debe dar todas sus ramas cerradas (con contradicciones):  Que en este caso es cierto, y por tanto sí se verifica la consecuencia lógica que nos preguntaba el enunciado.