**Algoritmos de Hormigas y el Problema del Viajante (TSP)**
En el vasto mundo de la optimización combinatoria, uno de los desafíos clásicos que ha desconcertado a matemáticos y científicos de la computación es el conocido como 'El problema del Viajante'. Esta incógnita plantea la pregunta de cómo encontrar la ruta más corta que visite un conjunto de ciudades exactamente una vez y regrese al punto de partida. ¿Cómo pueden las hormigas, en su aparentemente simple comportamiento, inspirar una solución a este problema? A través del estudio del Comportamiento Colectivo de las Hormigas en la Naturaleza y la posterior creación del Algoritmo de Optimización por Colonias de Hormigas (ACO), se ha encontrado una respuesta fascinante. En este blog, exploraremos desde la motivación detrás del problema del Viajante hasta las aplicaciones y variantes de este poderoso algoritmo inspirado en la naturaleza.
# Problema del Viajante
!!!side: [1]
Es un ejemplo que muestra la problemática que subyace tras algunos tipos de problemas matemáticos que, a priori, parecen tener una solución relativamente fácil, pero que, en la práctica, presentan un gran reto. La dificultad de este tipo de problemas no radica en que no se sepa cómo resolverlo, sino en la eficiencia de la solución que se conoce, ya que, hasta el momento, la solución no es factible debido al tiempo computacional que se precisa para obtenerla.
**El problema del viajante** (**TSP**: **Travelling Salesman Problem**) es uno de los problemas más famosos y estudiados en el campo de la optimización combinatoria computacional, ya que, a pesar de la aparente sencillez de su planteamiento, tiene una elevada complejidad en su resolución, haciéndolo comparable a otros problemas aparentemente mucho más complejos que han retado a los matemáticos desde hace siglos [1].
!!!Def: El problema del viajante
El problema del viajante consiste en encontrar la ruta más corta que puede realizar un viajante de negocios con el fin de visitar todas las ciudades (de un conjunto preestablecido de ciudades conectadas) una, y solo una, vez.
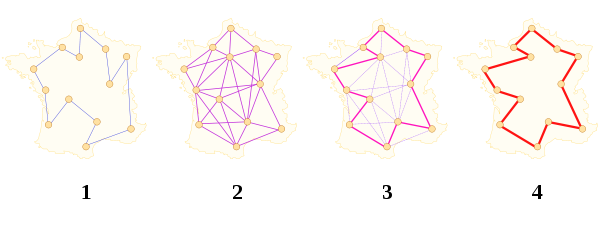
!!!side:[2]
Un *ciclo* es un camino cerrado en el grafo. Y se dice *Hamiltoniano* si pasa todos y cada uno de los nodos del grafo una sola vez.
Si se desea expresar el problema de forma matemática utilizando la [Teoría de Grafos](https://es.wikipedia.org/wiki/Teor%C3%ADa_de_grafos), el problema **TSP** propone encontrar en un grafo, $G$, que tiene asignado un **coste** (*longitud*, si se considera la interpretación estándar) para cada arista, el **ciclo Hamiltoniano** [2] que tenga la menor suma de costes de las aristas que lo componen.
Dentro de la **Teoría de la Complejidad**, que es la rama de la **Teoría de la Computación** que estudia, de manera teórica, la complejidad inherente a la resolución de problemas computables, este problema está catalogado como un problema **NP-completo**, lo que supone que los recursos computacionales necesarios para encontrar una solución óptima crecen de forma excesiva (normalmente, exponencial) con el tamaño de la entrada del problema.
!!!side:[3]
Basta un grafo simple de $7$ ciudades para que sea necesario calcular más de $5000$ combinaciones, ($7!=5040$), y si subimos hasta $10$ el número de ciudades del grafo, entonces las posibles rutas se disparan hasta más de tres millones ($10!=3.628.800$).
 En el caso concreto del problema **TSP** la entrada es el grafo (o conjunto de ciudades y sus conexiones). Cuanto mayor sea el número de nodos, mayor va a ser el número de rutas posibles y, por lo tanto, mayor será el esfuerzo requerido para dar la solución. Así, el número de rutas posibles entre $N$ nodos es igual a $N!$, lo que hace que la resolución del TSP mediante la obtención de todas las rutas posibles y posterior comparación entre ellas (que es el primer algoritmo que a uno se le ocurre para dar solución) es poco factible incluso para un número de nodos no muy elevado [3].
Por ello, intentar resolver TSP en grafos relativamente simples mediante el método de generación y comparación de todas las rutas es absolutamente inabordable mediante los medios computacionales disponibles actualmente, lo que hace que sea necesario utilizar otros procedimientos que, aunque no obtengan la solución óptima, sí proporcionen una respuesta aproximada lo suficientemente buena en un tiempo razonablemente bajo.
Mediante estas aproximaciones alternativas y no óptimas se han conseguido ciclos hamiltonianos en grafos con varios miles de nodos que solo se diferencian en un 1% de la solución óptima. Uno de estos métodos aproximados para resolver el TSP es el que presentamos aquí y que se inspira en la forma en que las colonias de hormigas resuelven el problema de búsqueda y recolección de alimentos.
# Hormigas en la Naturaleza
Se debe recordar que las hormigas son prácticamente ciegas y, sin embargo, moviéndose prácticamente al azar (o siguiendo leyes muy simples, que las convierten en autómatas de muy baja complejidad), acaban encontrando el camino más corto desde su nido hasta la fuente de alimentos (y regresar). Es importante hacer algunas consideraciones:
1. Por una parte, una sola hormiga no es capaz de realizar la tarea de encontrar un camino mínimo, sino que termina siendo un **resultado del hormiguero completo**, y
2. A pesar de la ceguera de cada hormiga, no lo hacen sin *instrumentos*, sino que una hormiga, cuando se mueve, deja una señal química en el suelo, depositando una sustancia denominada **feromona**, para que las demás puedan seguirla (así que complementan la carencia en un sentido por la mejora de otro de sus sentidos).
!!!side:4
Las [feromonas](https://es.wikipedia.org/wiki/Feromona) son sustancias químicas secretadas por los seres vivos, con el fin de provocar comportamientos específicos en otros individuos de la misma especie. Son un medio de transmisión de señales volátiles producidas en forma líquida, que luego se dispersan por el ambiente.
 En la naturaleza, las feromonas [4] cumplen un importante papel en la organización y supervivencia de muchas especies, y representan un sistema de comunicación química entre animales de una misma especie, informando acerca del estado fisiológico, reproductivo, social, edad, sexo y posible parentesco con el animal emisor.
Las feromonas han sido más estudiadas en insectos, como las hormigas y las abejas, que en animales superiores como los mamíferos, aunque se encuentran a todos los niveles de la jerarquía animal. Existen muchos tipos de feromonas, algunas son volátiles y cuentan con poca estabilidad y persistencia, pero tienen una mayor dispersión y un tiempo corto de acción, como las que segregan las hormigas o termitas durante un ataque a su nido. Además, existe otro tipo de feromonas que tienen poca volatilidad y una mayor estabilidad y persistencia, pero cuya dispersión es menor y con un mayor tiempo de acción, como son los hilos de plata que dejan los caracoles para poder regresar a su guarida, o las feromonas segregadas por las hormigas para guiar a las demás en la búsqueda de alimentos.
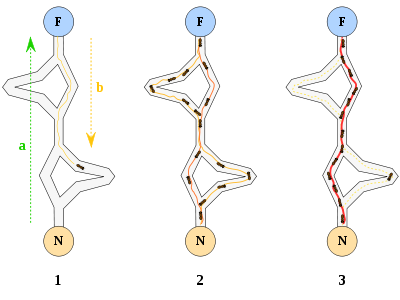
Los siguientes hechos explican, de forma intuitiva, por qué la forma de proceder de las hormigas genera caminos de coste mínimo entre los nidos y las fuentes de comida:
1. Una hormiga (**exploradora**) se mueve de manera aleatoria alrededor de la colonia.
2. Si encuentra una fuente de comida, retorna a la colonia de manera más o menos directa, dejando tras de sí un **rastro de feromonas**.
3. La intensidad de las feromonas determina la reacción de las hormigas-
4. Estas feromonas son atractivas, las hormigas más cercanas se verán atraídas por ellas y seguirán su pista de manera más o menos directa (lo que quiere decir que, a veces, pueden perder el rastro), que les lleva a la fuente de comida encontrada por la exploradora.
5. Al regresar a la colonia con alimentos estas hormigas depositan más feromonas, por lo que fortalecen las rutas de conexión.
6. Si existen dos rutas para llegar a la misma fuente de alimentos, en una misma cantidad de tiempo, la ruta más corta será recorrida por más hormigas que la ruta más larga.
7. En consecuencia, en la ruta más corta se aumentará en mayor proporción la cantidad de feromonas depositadas y será más atractiva para las siguientes hormigas.
8. La rutas más larga, menos visitadas, irán desapareciendo debido a que las feromonas son volátiles (**evaporación**) y son menos reforzadas.
9. Finalmente, todas las hormigas habrán determinado y escogido el **camino más corto**.
De esta forma, aunque una hormiga aislada (exploradora) se mueva esencialmente al azar, un grupo de ellas que pertenecen al mismo hormiguero decidirán sus movimientos considerando seguir con mayor frecuencia el camino con mayor cantidad de feromonas. Es decir, el resultado del comportamiento social del grupo es esencialmente distinto del resultado del comportamiento individual.
# ACO
Los **Algoritmos de Optimización por Colonias de Hormigas (ACO)** son una metodología inspirada en este tipo de **comportamiento colectivo** de las hormigas en su búsqueda de alimentos. Veamos cómo utilizar estas características comunicativas de las colonias de hormigas para resolver un problema computacionalmente duro como es el TSP.
En la solución que presentamos aquí vamos a suponer que todas las $N$ ciudades están conectadas entre sí (es decir, las $N$ ciudades forman un grafo completo).
!!!side:5
En $2$ dimensiones, entre las ciudades $C_i=(x^i_1,x^i_2)$ y $C_j=(x^j_1,x^j_2)$ el resultado será $d_{ij}=\sqrt{(x^i_1-x^j_1)^2 + (x^i_2-x^j_2)^2}$. En general, si las *ciudades* están en un espacio $n$-deimensional, entonces: $d_{ij}=\sqrt{\sum_{k=1}^n (x^i_k - x^j_k)^2}$.
Denotaremos estas ciudades por $\{C_1,\dots,C_N\}$, y denotaremos por $d_{ij}$ la distancia (el coste de la arista) entre las ciudades $C_i$ y $C_j$. De forma explícita, las ciudades pueden verse como puntos de un espacio de $2$ dimensiones (el número de dimensiones no es esencial), y la distancia entre ellas se calcula por medio de la distancia euclídea habitual [5].
En el caso más habitual, esta distancia es simétrica, es decir, tiene el mismo coste ir de $C_i$ a $C_j$ que de $C_j$ a $C_i$. Pero de todas formas, el algoritmo que vamos a explicar a continuación requiere muy pocas modificaciones si hay ciudades que no son accesibles desde otras, si los costes no se corresponden con las distancias euclídeas entre ellas (por ejemplo, si se considera como coste el precio del billete de tren entre las ciudades), o si dicho coste no es simétrico.
En esta solución, las hormigas van construyendo recorridos (posibles soluciones al problema TSP) moviéndose por el grafo de una ciudad a otra hasta que completan un ciclo. Para ello, en cada iteración del algoritmo, cada hormiga construye su recorrido ejecutando una regla de transición probabilista que indica qué nodo debe añadir al ciclo que está construyendo. El número de iteraciones máximo que se deja correr al algoritmo depende de la decisión del usuario, ya que no hay un mecanismo a priori que nos diga si alguna hormiga ya ha encontrado la solución óptima.
Para cada hormiga, la transición de la ciudad $i$ a la ciudad $j$ en una iteración del algoritmo depende de:
!!!side:6
Este paso puede traer complicaciones si no están disponibles todas las conexiones entre ciudades ya que, en ese caso, es posible comenzar a generar un recorrido que no tiene opciones de ser completado. Para resolver este problema, una solución podría ser, por ejemplo, que la hormiga elimina por completo el recorrido que está construyendo y comienza uno nuevo, pero hay otras opciones.
1. **Si la ciudad ha sido ya visitada o no, en el ciclo que está construyendo:** Cada hormiga mantiene en memoria las ciudades que ya ha visitado en el recorrido actual, y únicamente considera en cada paso las ciudades que no ha visitado todavía, que denotaremos por $J_i^k$ (ciudades no visitadas por la hormiga $k$ en esta iteración). De esta forma, aseguramos que al final la hormiga ha construido un recorrido válido [6].
!!!side:7
Normalmente, esta información suele ser estática, ya que las distancias de las ciudades son invariables a lo largo de la ejecución del algoritmo, pero es fácil imaginar escenarios en los que los costes de paso de un nodo a otro del grafo sean cambiantes y el algoritmo podría aplicarse para ir obteniendo buenas soluciones en este entorno dinámico.
2. **La inversa de la distancia a dicha ciudad, $\nu_{ij}=1/d_{ij}$, que es lo que se llama _visibilidad_:** Esta medida informa acerca de la bondad de escoger $C_j$ estando en $C_i$, y puede ser usada por las hormigas para que la distancia entre ciudades consecutivas sea una característica que intervenga en la selección del recorrido que está construyendo [7].
!!!side:8
A diferencia de la visibilidad, esta medida proporciona una información más global, ya que la feromona que tiene una arista indica lo buena que es esa arista en conjunción con otras para dar una buena solución.
3. **La cantidad de feromona que hay depositada en la arista que une ambos nodos, que denotaremos por $\tau_{ij}(t)$**: Esta cantidad se actualiza en cada paso, dependiendo de la cantidad de hormigas que han pasado por ella y de que el recorrido final de las hormigas que han usado esta conexión haya sido bueno (en relación con los demás caminos explorados). De alguna forma, mide la **inteligencia colectiva del hormiguero**, ya que es información que depende del conjunto de hormigas que están realizando la búsqueda [8].
A partir de las anteriores consideraciones, la **probabilidad de que la hormiga $k$ vaya de $C_i$ a $C_j$ en la construcción del recorrido actual**, viene dada por una expresión del tipo siguiente:
$$p_{ij}^k(t)=\frac{[\tau_{ij}(t)]^\alpha [\nu_{ij}]^\beta}{\sum_{l\in J_i^k} [\tau_{il}(t)]^\alpha [\nu_{il}]^\beta} \text{, si } j\in J_i^k$$
$$ p_{ij}^k(t)=0 \text{, si } j\notin J_i^k$$
Donde $\alpha$ y $\beta$ son dos parámetros ajustables que controlan el peso relativo de cada una de las medidas en la heurística resultante. Obsérvese que, para cada hormiga y en cada nodo/ciudad, los valores anteriores definen una función de probabilidad, ya que se ha normalizado para que la suma sea $1$. Además, hemos de tener en cuenta que:
* Si $\alpha=0$, en cada paso las ciudades más cercanas son las que tienen mayor probabilidad de ser seleccionadas, lo que se correspondería con el algoritmo voraz clásico en su versión estocástica (con múltiples puntos de inicio si, como veremos, las hormigas se colocan inicialmente en una ciudad al azar). En este caso, las hormigas no usan el conocimiento de la colonia para mejorar su comportamiento, que viene definido por la cantidad de feromona que hay en las aristas.
* Si $\beta=0$, únicamente interviene la feromona, lo que experimentalmente se comprueba que puede llevar a recorridos no muy buenos y sin posibilidad de mejora.
Por ello, parece que puede ser interesante una estrategia intermedia que mezcle ambas posibilidades, algo que se ha comprobado experimentalmente y que da sentido al hecho de haber formado las probabilidades anteriores como una combinación de ambas técnicas.
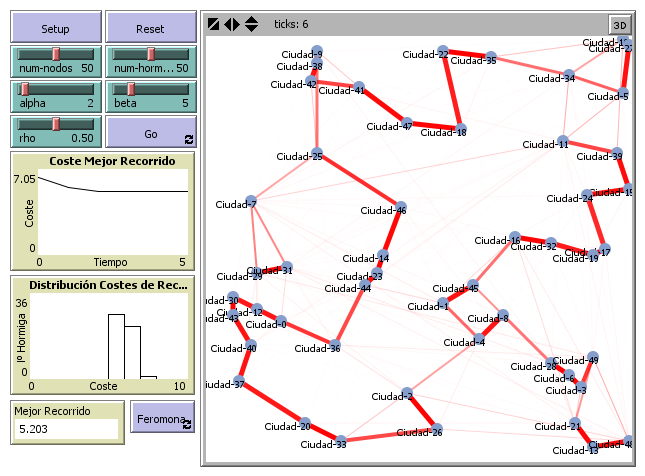
Con el fin de mejorar los recorridos más prometedores para el problema, y tras completar cada ciclo, cada hormiga deposita una cantidad de feromona, $\Delta\tau_{ij}^k(t)$, en cada una de las aristas del ciclo que ha construido. Esta cantidad dependerá de lo bueno que ha sido ese recorrido en comparación con el del resto de las hormigas.
Por ejemplo, si la hormiga $k$ ha realizado el recorrido $T^k(t)$, de longitud total $L^k(t)$, para cada par $(i,j)\in T^k(t)$, se puede hacer un depósito de feromona de $\Delta\tau_{ij}^k(t)=Q/L^k(t)$, donde $Q$ es un parámetro del sistema (en la práctica, este parámetro se ajusta para que la influencia de ambas estrategias sea compensada).
De esta forma, los recorridos más largos tendrán menos ganancia de feromona en sus aristas, lo que disminuirá su probabilidad relativa de ser seleccionados en etapas posteriores.
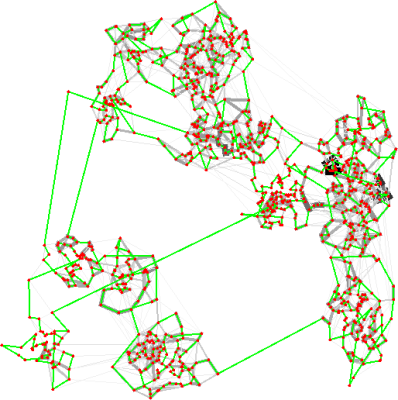
!!!side:9
Esta disminución en el tiempo de la cantidad de feromona refleja un hecho que ocurre en la realidad, y es que la feromona usada en este tipo de procesos se evapora con una cierta tasa en cuanto es depositada, de forma que es útil únicamente si recibe un refuerzo constante en cada tramo.
Para que este método funcione correctamente es necesario, además, dejar que la feromona no permanezca indefinidamente, sino que su influencia decaiga en el tiempo. Así, aquellas aristas que no vuelvan a ser visitadas por las hormigas (y que, por tanto, no son reforzadas), tendrán cada vez menos influencia en la heurística de decisión de cada paso [9].
Para conseguir este efecto, en los algoritmos de hormigas se introduce un nuevo parámetro, $0\leq \rho \leq 1$, junto con una regla de actualización de feromona como sigue:
$$\tau_{ij}(t) \leftarrow (1-\rho)\tau_{ij}(t) + \sum _{k=1}^M \Delta\tau_{ij}^k(t)$$
y se supone que, inicialmente, en todas las aristas hay una cantidad pequeña de feromona, $\tau_0$.
El número total de hormigas que intervienen, que hemos denotado por $M$ en la ecuación anterior, es otro parámetro importante a tener en cuenta:
* demasiadas hormigas tenderán rápidamente a reforzar recorridos que no son óptimos, por lo que puede ser difícil que el grupo los olvide y encontrar mejores opciones,
* muy pocas hormigas no provocarán el proceso de sinergia esperado, ya que no pueden contrarrestar el efecto de la evaporación de feromona, por lo que, finalmente, la solución que proporcionen sería equivalente al del algoritmo voraz estocástico.
Aunque no hay resultados teóricos que indiquen qué cantidad de hormigas es la óptima, una de las propuestas experimentales que más fuerza tiene es la de tomar tantas hormigas como ciudades haya ($M=N$), lo que supone un incremento lineal de los recursos de computación en función del dato de entrada.
| | |
|--|--|
|||
|||
!!!side:10
Si $M=N$, entonces la complejidad es $O(p\cdot N^3)$. Recuérdese que las soluciones completas y óptimas conocidas son exponenciales.
!!!Teorema:Teorema
Si al algoritmo anterior se le deja dar $p$ iteraciones, tenemos que la complejidad del algoritmo es $O(p\cdot M\cdot N^2)$ [10].
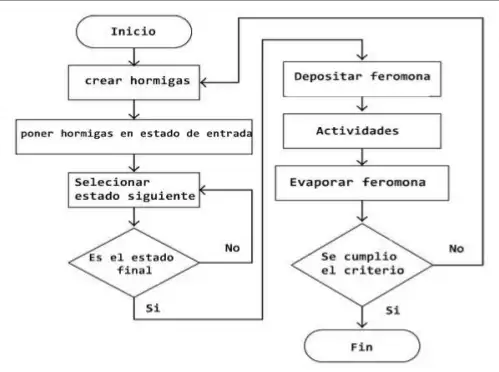
A grandes rasgos, el algoritmo que hemos seguido, y que puede servir de base para resolver otros problemas similares o hacer variantes, es el siguiente:
```none
Depositar una cantidad de feromona inicial en todas las aristas
Crear M hormigas
Repetir:
Reiniciar hormigas (borrar memoria)
Cada hormiga: Construir solución usando feromonas y coste de las aristas
Cada hormiga: Depositar feromonas en aristas de la solución
Evaporar feromona en las aristas
Devolver: la mejor solución encontrada
```
# Aplicaciones y Variantes
Aunque aquí hemos visto cómo aplicar colonias de hormigas a la resolución del problema TSP, es fácil imaginarse cómo adaptarlo para resolver otros muchos problemas sobre grafos que están relacionados con el cálculo de caminos mínimos (por ejemplo, el propio problema de encontrar caminos mínimos que se usa en búsquedas y optimización). En particular, podemos aplicarlo a problemas de optimización que se pueden proyectar en estructuras de grafos, como son los [Problemas de Satisfacción de Restricciones](CSP.md.html). En esta [otra entrada](Resolviendo_CSP_con_ACO.md.html) se da una idea general de cómo podría usarse la capacidad de las colonias de hormigas para minimizar caminos en la resolución CSPs genéricos.
!!!side:11
**AS**: M. Dorigo, V. Maniezzo, et A. Colorni, *Ant system: optimization by a colony of cooperating agents*, IEEE Transactions on Systems, Man, and Cybernetics--Part B , volume 26, numéro 1, pages 29-41, 1996.
**ACS**: M. Dorigo et L.M. Gambardella, *Ant Colony System : A Cooperative Learning Approach to the Traveling Salesman Problem*, IEEE Transactions on Evolutionary Computation, volume 1, numéro 1, pages 53-66, 1997.
**MMAS**: T. Stützle et H.H. Hoos, *MAX MIN Ant System*, Future Generation Computer Systems, volume 16, pages 889-914, 2000.
**PACO**: Chu S C, Roddick J F, Pan J S. *Ant colony system with communication strategies*. Information sciences, 2004, 167(1-4): 63-76.
**Opt. Recursiva**: Gupta, D.K.; Gupta, J.P.; Arora, Y.; Shankar, U., *Recursive ant colony optimization: a new technique for the estimation of function parameters from geophysical field data*, Near Surface Geophysics , vol. 11, no. 3, pp.325-339.
Estas son algunas de las variantes más populares de los algoritmos ACO [11].
* **Sistema de hormigas** (**AS**): fue el primer algoritmo ACO, que se corresponde con el presentado en las secciones anteriores.
* **Sistema de Colonia de hormigas** (**ACS**): Es una modificación que se basa en tres aspectos:
1. La selección de aristas se sesga hacia la explotación: se favorece la probabilidad de seleccionar las aristas más cortas con una gran cantidad de feromona.
2. Mientras construyen una solución, las hormigas cambian el nivel de feromona de las aristas que están seleccionando aplicando una regla local de actualización de feromona.
3. Al final de cada iteración, solo la mejor hormiga puede actualizar los caminos aplicando una regla global modificada de actualización de feromona.
* **Sistema de Colonia Asíncrona**: Todas las hormigas dejan la misma cantidad de feromona, independientemente de la bondad de la solución, pero la ejecución no es sincronizada, sino que las hormigas que acaban antes pueden volver a comenzar una nueva generación de camino. De esta forma, los caminos más cortos, tendrán más posibilidad de ser repetidos. Es un mecanismo más similar al que aparece en la naturaleza.
* **Sistema Elitista de Hormigas**: la mejor solución global deposita feromona en su camino después de cada iteración (incluso si este camino no ha sido revisitado en esta iteración), junto con las soluciones obtenidas por todas las hormigas. La estrategia elitista tiene como objetivo dirigir la búsqueda de todas las hormigas para construir una solución que contenga enlaces de la mejor ruta actual.
* **Sistema de Hormigas Max-Min** (**MMAS**): Esta variante controla las cantidades máximas y mínimas de feromona en cada recorrido. Solo el mejor recorrido global o el mejor recorrido de iteración pueden añadir feromona a su rastro. Para evitar el estancamiento del algoritmo de búsqueda, el rango de posibles cantidades de feromona en cada ruta se limita a un intervalo $[\tau_{max}, \tau_{min}]$. Todas las aristas se inicializan a $\tau_{max}$ para forzar una mayor exploración de soluciones. Los caminos se reinicializan a $\tau_{max}$ cuando se acercan al estancamiento.
* **Sistema de Hormigas basado en Rangos** (**ASrank**): Todas las soluciones se clasifican según su longitud, posteriormente, solo a un número fijo de las mejores hormigas de esta iteración se les permite actualizar sus ensayos. La cantidad de feromona depositada se pondera para cada solución, de forma que las soluciones con caminos más cortos depositan más feromona que las soluciones con caminos más largos.
* **Optimización Paralela de Colonias de Hormigas** (**PACO**): Añade estrategias de comunicación.
* **Optimización Recursiva de Colonias de Hormigas**: Es una forma recursiva de sistema de hormigas que divide todo el dominio de búsqueda en varios subdominios y resuelve el objetivo en estos subdominios. Los resultados de todos los subdominios se comparan y unos pocos de ellos son promovidos para el siguiente nivel, que se vuelven a subdividir y el proceso se repite hasta que se obtiene un resultado de la precisión deseada.
Para algunas versiones del algoritmo, se puede demostrar que es convergente (es decir, que es capaz de encontrar el óptimo global en tiempo finito). La primera prueba de convergencia fue en 2000 para el algoritmo de sistema de hormigas basado en grafos, y posteriormente se consiguió para los algoritmos ACS y MMAS. Como suele ser habitual en el tema de las metaheurísticas, es muy difícil demostrar la convergencia y estimar la velocidad teórica de convergencia, pero se ha mostrado que su rendimiento y su velocidad de convergencia son sensibles a los valores de los parámetros de los modelos, especialmente al valor de la tasa de evaporación de feromona. Posteriormente, se ha demostrado que algunas variantes son equivalentes a métodos de descenso de gradiente estocástico, o al de entropía cruzada.
(insert menu.md.html here)