**Algoritmos Genéticos**
Desde los albores de la informática, los científicos informáticos han buscado inspiración en la naturaleza para resolver problemas complejos. Uno de los frutos más fascinantes de esta búsqueda es el desarrollo de los Algoritmos Genéticos (AG). Estos algoritmos, inspirados en la evolución biológica, han demostrado ser una poderosa herramienta para encontrar soluciones óptimas en una variedad de problemas, desde la optimización de funciones hasta el diseño de redes neuronales. En esta entrada, exploraremos desde sus fundamentos hasta sus aplicaciones más avanzadas, abordando su historia, su formalización matemática, y los diversos métodos que conforman esta técnica de búsqueda y optimización.
# Historia de la Computación Evolutiva
Los primeros ejemplos de lo que hoy podríamos llamar algoritmos genéticos aparecieron a finales de los 50 y principios de los 60, y fueron programados en computadoras por biólogos evolutivos que buscaban explícitamente el modelado de algunos aspectos de la evolución natural. A ninguno de ellos se le ocurrió que esta estrategia podría aplicarse de manera más general a los problemas artificiales, pero esa aproximación no tardaría en llegar: *la computación evolutiva estaba filtrándose en el entorno de computación desde los primeros días de la computadora electrónica*.
En 1962, investigadores como G.E.P. Box, G.J. Friedman, W.W. Bledsoe y H.J. Bremermann habían desarrollado independientemente algoritmos inspirados en la evolución para optimización de funciones y aprendizaje automático, pero sus trabajos produjeron poca reacción en el resto del área. En 1965 surgió un desarrollo más exitoso, cuando Ingo Rechenberg, entonces de la Universidad Técnica de Berlín, introdujo una técnica que llamó **estrategia evolutiva**, aunque, a pesar de su nombre, hoy en día lo asociaríamos más a los algoritmos de ascenso de la colina que a los algoritmos genéticos: en su técnica no había población ni cruzamiento; un padre mutaba para producir un descendiente, y se conservaba el mejor de los dos, convirtiéndose en el padre de la siguiente ronda de mutación. Versiones posteriores introdujeron la idea de población.
El siguiente desarrollo importante en el campo vino en 1966, cuando L.J. Fogel, A.J. Owens y M.J. Walsh introdujeron una técnica que llamaron **programación evolutiva**. En este método, las soluciones candidatas para los problemas se representaban como máquinas de estado finito sencillas; al igual que en la estrategia evolutiva de Rechenberg, su algoritmo funcionaba mutando aleatoriamente una de estas máquinas simuladas y conservando la mejor de las dos (padre e hija). Sin embargo, lo que todavía faltaba en estas dos metodologías era reconocer la importancia del cruzamiento.
!!!side:1
J. H. Holland. *Adaptation in Natural and Artificial Systems*, University of Michigan Press, Ann Arbor. 1975.
!!!side:2
En el contexto de la optimización, un *paisaje* se refiere a la representación gráfica o conceptual de una función objetivo en un espacio multidimensional. Este paisaje muestra cómo cambia el valor de la función objetivo en relación con diferentes combinaciones de variables de decisión. Puede tener picos (soluciones óptimas), valles (áreas con valores relativamente bajos) y mesetas (áreas con valores constantes). Comprender el paisaje es esencial para elegir y diseñar algoritmos de optimización efectivos, ya que afecta la búsqueda de soluciones óptimas.
 Aunque es en 1962 cuando el trabajo de John Holland sobre sistemas adaptativos establece las bases para los desarrollos que vendrán posteriormente (y más importante, siendo el primero en proponer explícitamente el **cruzamiento** y otros operadores de **recombinación**), no sería hasta 1975 que aparece el trabajo fundamental en el campo de los algoritmos genéticos, con la publicación del libro *Adaptación en Sistemas Naturales y Artificiales* [1]. Basado en investigaciones y papers anteriores del propio Holland y de colegas de la Universidad de Michigan, este libro fue el primero en presentar sistemática y rigurosamente el concepto de **sistemas digitales adaptativos** utilizando las operaciones de **mutación**, la **selección** y el **cruzamiento**, y simulando el proceso de la evolución biológica como estrategia para resolver problemas. El libro también intentó colocar los algoritmos genéticos sobre una base teórica firme introduciendo el concepto de **esquema**. Ese mismo año, la importante tesis de Kenneth De Jong estableció el potencial de los Algoritmos Genéticos demostrando que podían desenvolverse bien en una gran variedad de funciones de prueba, incluyendo *paisajes de optimización* [2] ruidosos, discontinuos y multimodales.
!!!side:3
El **problema de la mochila** es un problema clásico del campo de la optimización combinatoria. Tiene aplicaciones prácticas en muchas situaciones del mundo real: desde la gestión de recursos en logística, hasta la planificación financiera y la optimización de recursos en ingeniería. Se plantea de la siguiente manera:
*Imagina que tienes una mochila con una capacidad de peso limitada y una lista de objetos, cada uno con un peso y un valor específicos. El objetivo es determinar la combinación de objetos que puedes colocar en la mochila de manera que maximices el valor total de los objetos, sin exceder la capacidad de peso de la mochila.*
Por otra parte, el **problema de coloración de grafos** es otro problema clásico en teoría de grafos y optimización combinatoria que tiene aplicaciones en diversas áreas, como la asignación de frecuencias en la planificación de redes, la programación de horarios, y la asignación de recursos en problemas de asignación. Se plantea de la siguiente manera:
*Dado un grafo, el objetivo es asignar un color a cada nodo de manera que los nodos adyacentes no tengan el mismo color. La pregunta es: ¿cuál es el menor número de colores que se necesitan? Este número mínimo de colores necesarios se conoce como el *número cromático* del grafo.
Estos trabajos fundacionales establecieron un interés más generalizado en la computación evolutiva. Entre principios y mediados de los 80, los algoritmos genéticos se estaban aplicando en una amplia variedad de áreas, desde problemas matemáticos abstractos, como el **problema de la mochila** (bin-packing) y la **coloración de grafos** [3], hasta asuntos tangibles de ingeniería como el control de flujo en una línea de montaje, reconocimiento y clasificación de patrones y optimización estructural.
Al principio, estas aplicaciones eran principalmente teóricas. Sin embargo, con el paso del tiempo y los avances realizados en investigación, migraron hacia el sector comercial, en paralelo con el crecimiento exponencial de la potencia de computación y el desarrollo de Internet. Hoy en día, la computación evolutiva es un campo floreciente, y los algoritmos genéticos están resolviendo problemas de interés cotidiano en áreas de estudio tan diversas como la predicción en la bolsa y la planificación de la cartera de valores, ingeniería aeroespacial, diseño de microchips, bioquímica y biología molecular, diseño de horarios y líneas de montaje. La potencia de la evolución ha tocado virtualmente cualquier campo que imaginemos, modelando invisiblemente el mundo que nos rodea, y siguen descubriéndose nuevos usos integrados con otras técnicas que han tomado fuerza posteriormente. Y en el corazón de todo esto se halla nada más que la simple y poderosa idea de Charles Darwin: **que el azar en la variación, junto con la ley de selección, es una técnica de resolución de problemas de inmenso poder y de aplicación casi ilimitada**.
Aunque a continuación veremos los Algoritmos Genéticos como máximos representantes de estas ideas, hay otros muchos ejemplos en los que se pueden utilizar las ideas de selección por supervivencia para conseguir optimizaciones de problemas. Basándose en la idea de que los más aptos sobreviven mejor a las situaciones del entorno, es posible crear simulaciones en las que los individuos están obligados a sobrevivir en un ambiente hostil, y solo aquellos con las condiciones más adecuadas para ese entorno serán capaces de durar el tiempo suficiente para reproducirse (sea sexual o asexualmente) y dejar descendencia en la que sus caracteres positivos den más opciones a los nuevos individuos, que junto con la mutación, puede producir una paulatina adaptación al medio. Tras este proceso durante generaciones, los individuos que queden reflejarán en sus características una solución (cuasi) óptima al problema de la supervivencia en el entorno.
# ¿Qué es un Algoritmo Genético?
!!!side:4
Aunque estas candidatas iniciales pueden ser soluciones cuya calidad se conoce a priori, con el objetivo de que el AG las mejore, lo más común es generarlas aleatoriamente, y de esa forma reducir el sesgo que pueda tener el conocimiento previo en la búsqueda de una solución óptima.
Brevemente, un **Algoritmo Genético** (**AG**) es _una técnica de resolución de problemas que se inspira en la evolución biológica como estrategia para la resolución_, englobándose dentro de lo que antes hemos denominado *técnicas basadas en poblaciones*. Dado un problema específico a resolver, la entrada del AG es un conjunto de soluciones potenciales a ese problema, codificadas de alguna manera, y una métrica llamada **función de aptitud**, o **fitness**, que permite evaluar cuantitativamente la bondad de cada solución candidata [4].
A partir de ahí, AG evalúa cada candidata de acuerdo con la función de aptitud. Por supuesto, se debe tener en cuenta que estas primeras candidatas mostrarán baja eficiencia con respecto a la resolución del problema, y la mayoría no funcionarán en absoluto. Sin embargo, por puro azar, unas pocas pueden ser prometedoras, pudiendo mostrar algunas características que muestren, aunque solo sea de una forma débil e imperfecta, cierta capacidad de solución del problema.
Estas candidatas prometedoras se conservan y se les permite reproducirse. Se realizan múltiples copias de ellas, pero estas copias no son perfectas, sino que se les introducen algunos cambios aleatorios durante el proceso de copia, a modo de las **mutaciones** que pueden sufrir los descendientes de una población. Luego, esta descendencia digital prosigue con la siguiente generación, formando un nuevo conjunto de soluciones candidatas, y son de nuevo sometidas a una ronda de **evaluación** de aptitud. Las candidatas que han empeorado o no han mejorado con las mutaciones son eliminadas de nuevo; pero, de nuevo, por puro azar, las variaciones aleatorias introducidas en la población pueden haber mejorado a algunos individuos, convirtiéndolos en mejores soluciones del problema, más completas o más eficientes. El proceso se repite las iteraciones que haga falta, hasta que obtengamos soluciones suficientemente buenas para nuestros propósitos. Puede mejorarse el proceso de evolución permitiendo que las características individuales de las soluciones se combinen por medio de operaciones de **cruzamiento** para generar nuevos descendientes (simulando lo que sería la reproducción sexual).

Podemos dar una primera formalización del proceso anterior por medio del siguiente pseudocódigo:
```
AG:
Crea población inicial
Evalúa los cromosomas de la población inicial
Repite hasta que se cumpla la condición de parada
Selección de los cromosomas más aptos en la nueva población
Cruzamiento de los cromosomas de la población
Mutación de los cromosomas de la población
Evaluación de los cromosomas de la población
Devuelve la mejor solución (la más apta) en la población
```
Aunque pueda parecer asombroso, anti-intuitivo, y quizás como algo de suerte y magia, los AG han demostrado ser una estrategia enormemente poderosa y exitosa para resolver problemas, mostrando de manera espectacular el poder de los principios evolutivos. Además, las soluciones que consiguen son a menudo más eficientes, más elegantes o más complejas que las que un humano produciría.
# Formalización de AG
!!!side:5
Como $max{f(x)} = -min{-f(x)}$ trataremos en esta entrada el problema de optimización como un problema de minimización, sin pérdida de generalidad. Ha de tenerse presente que la existencia de este óptimo no se asegura y, en general, depende de las características de $f$ y de $D$.
!!!def: Problema de Optimización
Dado un dominio, $D$, y una función $f: D → \mathbb{R}$, el problema de la optimización de $f$ consiste en encontrar el mejor valor de $f$ en el dominio $D$, es decir, encontrar $x^* ∈ D$ tal que [5]
$$f(x^*)=min_D f$$
En general, la tarea de optimización se complica debido a la existencia de óptimos locales (mínimos locales en nuestro caso).
!!!def: Mínimos Locales
La función $f$ tiene un mínimo local en $x' ∈ D$ si existe $E$, entorno de $x$, tal que
$$f(x')=min_E f$$
!!!side:6
La inyectividad de $e$ es necesaria matemáticamente para que exista la inversa (al menos, parcialmente), y desde un punto de vista intuitivo es la que nos permite que los objetos de $D$ sean recuperables a partir de su codificación.
!!!def: Representación (codificación)
Sea $S$ un conjunto (llamado **alfabeto**). Diremos que $e : D → S^k$, inyectiva, es una representación/codificación de $D$ [6]. A $S^k$ se le denomina *espacio de búsqueda*. A la función $g:S^k → \mathbb{R}$, $g=f\circ e^{-1}$ se le denomina *función objetivo*.
El AG examinará un subconjunto del espacio de búsqueda, obteniendo una representación $x^*$ tal que $g(x^*)=min_{S^n} g$
!!!side:7
La función objetivo interviene normalmente en la definición de $sel$ (en algunas variantes se utiliza para seleccionar los padres) y de $red$ (en el proceso de desechar los individuos que no formarán parte de la generación siguiente).
La función $mut$ suele venir dada por la aplicación punto a punto (individuo a individuo) de una función de mutación individual, $mut'$, de forma que $mut(P)=map(mut',P)$.
!!!def:Algoritmo Genético
Un **Algoritmo Genético** de objetivo $g$ sobre el alfabeto $S$ es una función generadora de poblaciones que sigue el esquema:
$$AG(t)=\begin{cases}
P_0 & \mbox{, si } t=0\\
red(P_{t-1} \cup mut\circ rep\circ sel(P_{t-1})) & \mbox{, si t > 0}
\end{cases}$$
donde [7]:
* $k$ es la longitud de la representación,
* $n$ es el tamaño de la población,
* $P_0 \in (S^k)^n$ es la población inicial,
* $sel: (S^k)^n → (S^k)^n \times (S^k)^n$ es la función de selección (de los que serán padres de la siguiente generación), verificando $sel(P)\subseteq P\times P$,
* $rep: (S^k)^n \times (S^k)^n → (S^k)^n$ es la función de reproducción sexual,
* $mut: (S^k)^n \to (S^k)^n$ es la función de mutación,
* $red: (S^k)^{2n} \to (S^k)^n$ es la función encargada de reducir el tamaño de la población en cada paso.
# Métodos de representación
!!!side:8
Por su similitud con el proceso de evolución genética, a los individuos que representan posibles soluciones en AG se les denomina muchas veces *cromosomas*. Siguiendo con la analogía, es común denominar *gen* a cada una de las unidades de información que conforman este cromosoma, y que pueden representar características aisladas e independientes de la solución, por ejemplo: coeficientes de un polinomio, o color asignado a cada nodo de un grafo. En términos biológicos, el conjunto de parámetros representando un cromosoma particular se denomina *fenotipo*, que contiene la información requerida para construir un organismo, al que se denomina *genotipo*.
 Como hemos visto, la definición de AG requiere de una función para codificar las soluciones potenciales del problema, de forma que el propio algoritmo pueda procesarlas aplicando las operaciones formales que le permiten evolucionar ($sel$, $rep$, $mut$ y $red$). Un enfoque común es codificar las soluciones como cadenas binarias: secuencias de $1$'s y $0$'s, donde el dígito de cada posición representa la presencia/ausencia de algún aspecto de la solución. Otro método similar consiste en codificar las soluciones como vectores/cadenas de números enteros o decimales donde cada posición, de nuevo, representa algún aspecto particular de la solución. Esta última representación ofrece mayor precisión y complejidad que la representación binaria, y a menudo está intuitivamente más cerca del espacio de soluciones del problema, pero también hace más compleja la búsqueda de soluciones óptimas en el paisaje de optimización. En muchas otras ocasiones se consideran palabras de un alfabeto prefijado, de forma similar a como la información genética se codifica por medio del alfabeto ${A,C,G,T}$ [8].
El objetivo de cualquier representación es posibilitar y facilitar la definición de los operadores encargados de los cambios en las soluciones candidatas seleccionadas (poblaciones): intercambiar $0$ por $1$, sumar o restar al valor de un número una cantidad elegida al azar, o cambiar una letra por otra.
!!!side:9
Un **árbol** en teoría de grafos es un tipo de grafo no dirigido acíclico y conexo, lo que significa que no tiene ciclos y todos los nodos están conectados. Representa la estructura de grafo más simple y fundamental en la que todos los nodos están interconectados de manera única sin formar circuitos cerrados (entre cualquier par de nodos del árbol existe exactamente un camino único que los conecta). Los árboles se utilizan en diversas aplicaciones, como en algoritmos de búsqueda y como estructura de datos fundamental para muchos otros algoritmos. Muy comúnmente, se suele dar una representación *enraizada* del árbol.
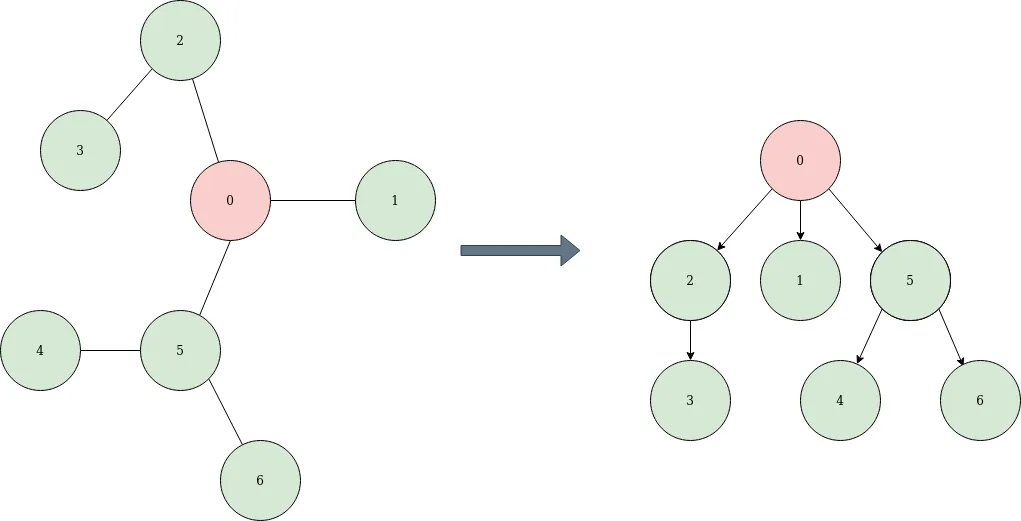
Otra estrategia, desarrollada principalmente por John Koza, de la Universidad de Stanford, y denominada **programación genética**, manipula como individuos de la población programas de un determinado lenguaje (por ejemplo, LISP) por medio de **árboles** [9]. En este método, los nodos-hoja representan datos (o estructuras de datos) y los nodos interiores son operadores/instrucciones válidas en el lenguaje. Las variaciones que puede sufrir un individuo pueden conseguirse cambiado un nodo de tipo operador, alterando el valor de un cierto nodo del árbol, o sustituyendo un subárbol por otro.

Concretando un poco lo que hemos comentado en los párrafos anteriores, debe tenerse en cuenta que la elección adecuada de cómo representar los cromosomas es fundamental para el desempeño y la eficacia del algoritmo. Algunos métodos comunes de representación son:
1. **Representación Binaria:** Los cromosomas son representados como cadenas de bits (0s y 1s). Cada gen en el cromosoma corresponde a un bit. Esta representación es especialmente útil cuando las soluciones pueden ser codificadas como combinaciones de valores booleanos o enteros.
2. **Representación Entera:** Los cromosomas son representados como secuencias de enteros. Cada gen en el cromosoma representa un número entero que puede ser interpretado como una característica, índice o valor en el espacio de búsqueda del problema.
3. **Representación Real (o de Punto Flotante):** Los cromosomas son representados como secuencias de números de punto flotante. Esto se utiliza cuando las soluciones deben estar en un rango continuo de valores. Los genes pueden representar parámetros reales, como temperaturas o coordenadas geográficas.
4. **Representación Alfabética:** Los cromosomas son representados como secuencias de elementos de un alfabeto prefijado. Aunque es equivalente a la representación entera, es tan común que conviene identificarla como un método propio. Realmente, el resto de representaciones se pueden interpretar como casos particulares de este, donde usaríamos el alfabeto binario ($\{0,1\}$), entero ($\mathbb{Z}$), real ($\mathbb{R}$), etc.
4. **Representación Permutacional:** Los cromosomas son representados como permutaciones de un conjunto de elementos. Esta representación es útil para problemas en los que la secuencia o el orden de los elementos son importantes, como en el problema del agente viajero, donde el orden de las ciudades a visitar es crucial.
5. **Representación Basada en Árboles:** Los cromosomas son representados como estructuras de árbol. Esta representación se utiliza en problemas donde las soluciones pueden ser representadas de manera jerárquica. En ciertas ocasiones (como en la programación evolutiva) los nodos interiores del árbol representan operadores o funciones, las hojas son datos, y las aristas de padres a hijos representan relación de aplicacibilidad entre unos y otros.
6. **Representación Híbrida:** En algunos casos, se pueden utilizar múltiples tipos de representaciones en un solo cromosoma. Por ejemplo, una parte del cromosoma puede ser binaria y otra parte puede ser entera. Esto se hace para manejar diferentes tipos de variables en un problema de optimización.
La elección de la representación de los cromosomas depende del problema específico que se está abordando y de cómo las soluciones pueden ser mejor expresadas. Una representación adecuada puede mejorar significativamente la capacidad del algoritmo genético para encontrar soluciones óptimas o cuasi-óptimas en el espacio de búsqueda del problema. Aunque, como hemos visto, el alfabeto utilizado para representar los individuos no tiene por qué ser obligatoriamente el binario, gran buena parte de la teoría desarrollada para AG utiliza este alfabeto.
# Métodos de selección
!!!side:10
Obsérvese que es fácil dar una formalización de $sel$ en cada caso.
Un algoritmo genético puede utilizar muchas técnicas diferentes para seleccionar a los individuos que deben copiarse hacia la siguiente generación. Algunas de las más habituales son (debe tenerse en cuenta que algunos son mutuamente excluyentes, mientras que otros se pueden combinar) [10]:
* **Selección elitista**: se garantiza la selección de los miembros más aptos de cada generación (la mayoría de los AGs no utilizan elitismo puro, sino una forma modificada por la que el individuo mejor, o algunos de los mejores, son copiados hacia la siguiente generación en caso de que no surja nada mejor).
* **Selección proporcional a la aptitud**: los individuos más aptos tienen más probabilidad de ser seleccionados, pero no la certeza.
* **Selección por rueda de ruleta**: una forma de selección proporcional a la aptitud en la que la probabilidad de que un individuo sea seleccionado es proporcional a la diferencia entre su aptitud y la de sus competidores.
* **Selección escalada**: al incrementarse la aptitud media de la población, la fuerza de la presión selectiva también aumenta y la función de aptitud se hace más discriminadora. Este método puede ser útil para seleccionar para valores mayores de $t$, cuando todos los individuos tengan una aptitud relativamente alta y sólo les distingan pequeñas diferencias en la aptitud.
* **Selección por torneo**: se eligen subgrupos de individuos de la población, y los miembros de cada subgrupo compiten entre ellos. Sólo se elige a un individuo de cada subgrupo para la reproducción.
* **Selección por rango**: a cada individuo de la población se le asigna un rango numérico basado en su aptitud, y la selección se basa en este ranking, en lugar de las diferencias absolutas en aptitud. La ventaja de este método es que puede evitar que individuos muy aptos ganen dominancia al principio a expensas de los menos aptos, lo que reduciría la diversidad genética de la población y podría obstaculizar la búsqueda de una solución aceptable.
* **Selección generacional**: la descendencia de los individuos seleccionados en cada generación se convierte en toda la siguiente generación. No se conservan individuos entre las generaciones.
* **Selección jerárquica**: los individuos atraviesan múltiples rondas de selección en cada generación. Las evaluaciones de los primeros niveles son más rápidas y menos discriminatorias, mientras que los que sobreviven hasta niveles más altos son evaluados más rigurosamente. La ventaja de este método es que reduce el tiempo total de cálculo al utilizar una evaluación más rápida y menos selectiva para eliminar a la mayoría de los individuos que se muestran poco o nada prometedores, y sometiendo a una evaluación de aptitud más rigurosa y computacionalmente más costosa solo a los que sobreviven a esta prueba inicial.
# Métodos de reproducción
Una vez que la selección ha elegido a los individuos aptos, estos deben mezclarse con el objetivo de conseguir nuevas soluciones que presenten buenas características de combinaciones de la generación anterior (reproducción sexual).
El método más habitual se basa en lo que se llama **cruzamiento**, y consiste en seleccionar a dos individuos para que intercambien segmentos de su código genético, produciendo una *descendencia* artificial cuyos individuos son combinaciones de sus padres. Este proceso pretende simular el proceso análogo de la recombinación que se da en los cromosomas durante la reproducción sexual. Las formas comunes de cruzamiento incluyen:
* **Cruzamiento de un punto**, en el que se establece un punto de intercambio en un lugar aleatorio del genoma de los dos individuos, y uno de los individuos contribuye todo su código anterior a ese punto y el otro individuo contribuye todo su código a partir de ese punto para producir una descendencia.

* **Cruzamiento en dos puntos**, en el que se intercambian los genes que aparecen en el intervalo de genes delimitados por dos puntos.

* **Cruzamiento uniforme**, en el que el valor de una posición dada en el genoma de la descendencia corresponde al valor en esa posición del genoma de uno de los padres o al valor en esa posición del genoma del otro padre, elegido con un 50% de probabilidad.

# Métodos de mutación
!!!side:11
Normalmente, por un proceso aleatorio que decide qué gen cambiará y qué valor tendrá tras la mutación.
Una vez que la selección ha elegido a los individuos aptos, estos deben ser alterados aleatoriamente con la esperanza de mejorar su aptitud para la siguiente generación. La estrategia más sencilla es la que se conoce como **mutación**. Al igual que una mutación en los seres vivos cambia un gen por otro, una mutación en un algoritmo genético también causa pequeñas alteraciones en puntos concretos de la codificación del individuo [11].

# Desventajas y limitaciones
!!!side:12
Aunque, finalmente, el paralelismo dependerá de la implementación concreta que se haga.
El hecho de que los Algoritmos Genéticos efectúen buenas búsquedas, se debe a que implícitamente muestrean hiperplanos del espacio de codificación. Por ejemplo, cada individuo representado por medio de una codificación binaria, se corresponde con un vértice del hipercubo que representa el espacio de búsqueda, y forma parte de $2^k-1$ diferentes hiperplanos (existen un total de $3^k-1$ hiperplanos posibles sobre el espacio de búsqueda binario completo). Por ello, cada individuo no proporciona gran información si se examina por separado, sino que precisa de la información conjunta con el resto de individuos. Es por ello que la búsqueda basada en una población es crítica para los Algoritmos Genéticos. Una población de individuos proporciona información sobre numerosos hiperplanos simultáneamente. El hecho de que se muestreen muchos hiperplanos cuando se evalúa una población de codificaciones se asocia al *paralelismo implícito* o *intrínseco* de los Algoritmos Genéticos [12].
A pesar de las bondades apuntadas para este tipo de algoritmos, debemos mencionar algunas de las limitaciones que presentan:
* Como ocurre en muchos problemas de optimización, si tiene una alta complejidad entonces **la función de evaluación puede resultar demasiado costosa** en términos de tiempo y recursos.
* Hay casos en los que, dependiendo de los parámetros que se utilicen para la evaluación, **el algoritmo puede no converger a una solución óptima**, o bien terminar en una convergencia prematura con resultados no satisfactorios (es decir, devolviendo un óptimo local o incluso un punto arbitrario).
* **No poseen una buena escalabilidad** con la complejidad. En sistemas en los que intervienen muchas variables, el espacio de búsqueda asociado puede crecer de manera exponencial debido, entre otras cosas, a las relaciones no lineales que puedan surgir entre los subconjuntos de variables.
* La mejor solución lo es solo en comparación a otras soluciones, por lo que no se tiene demasiado claro un criterio de cuándo detenerse, ya que no se cuenta con una solución específica que sirva de referencia.
* No es recomendable su uso para problemas que buscan respuesta a problemas con soluciones simples como Sí/No o problemas de decisión, ya que el algoritmo difícilmente convergerá y el resultado será casi aleatorio.
* El diseño de la función de aptitud (fitness) y la selección de los criterios de mutación entre otros, necesitan de cierta pericia y **conocimiento previo del problema** para obtener buenos resultados.
!!!side:13
Algo especialmente limitante cuando tratamos de usarlos en soluciones orientadas a la creación de Inteligencia Artificial.
* La representación depende completamente del problema a resolver, por lo que difícilmente es automatizable para incluirlo en cadenas de procesos para solución de problemas complejos, planificación, deliberacíón, etc. [13]
(insert menu.md.html here)