**Espacios de Estados** En el campo de la inteligencia artificial, la resolución de problemas y la planificación son dos áreas cruciales que han sido abordadas con métodos diversos y poderosos. Comenzaremos esta exploración adentrándonos en la noción de Problemas y Estados, estableciendo el escenario para entender cómo los sistemas pueden buscar soluciones a través de diferentes estados. A partir de aquí, nos adentraremos en las Búsquedas en Espacios de Estados, examinando cómo los algoritmos pueden navegar a través de estos espacios para encontrar soluciones óptimas. También exploraremos cómo los Espacios pueden ser representados como Árboles y Grafos, proporcionando estructuras visuales que facilitan la comprensión y el análisis. Luego, nos sumergiremos en Problemas de Planificación, donde la tarea es encontrar secuencias de acciones que transformen un estado inicial en un estado objetivo. Para ilustrar estos conceptos, exploraremos varios Ejemplos, desde CSPs hasta Puzzles clásicos como el de piezas deslizantes, Misioneros y Caníbales, y Todos los Dígitos del Rey. Finalmente, evaluaremos la Evaluación y Rendimiento de los algoritmos en estos contextos, analizando cómo se desempeñan en términos de tiempo y espacio en la resolución de problemas de búsqueda y planificación. # Problemas y Estados Sin lugar a dudas, una de las principales características que reconocemos en la inteligencia es la capacidad para resolver problemas. Si consideramos una inteligencia como la humana, a la habilidad para analizar los elementos intrínsecos de cada problema, que está presente también en muchas otras especies animales, se añade la **capacidad de abstraer e identificar las acciones que se pueden realizar** sobre él para resolverlo. En un nivel incluso superior de abstracción, reconocible solo en las llamadas especies superiores, podemos considerar también la capacidad de determinar cuál puede ser, de entre los posibles métodos que se idean, el más adecuado, ya sea en términos de tiempo, de recursos, de seguridad para el individuo, etc. De esta forma, aparece una triple capacidad de **análisis**, **abstracción** y **estrategia** que sitúa el tema general de la resolución de problemas en el núcleo de la inteligencia artificial y, por ello, no resulta extraño que se consideren deseables para cualquier individuo, artificial o no, que queramos que se comporte inteligentemente. Podemos pensar en una variedad de problemas que van desde cómo alcanzar una fuente de comida situada a cierta distancia y a la que no se puede ir directamente, hasta cómo resolver un pequeño juego como podría ser el famoso cubo de Rubik, o resolver el problema matemático de encontrar la solución a una ecuación numérica. En todos ellos encontramos elementos comunes tras un proceso de abstracción que nos permiten de forma general definir la **resolución de problemas** como: !!!def:Resolución de Problemas El proceso que, partiendo de una situación inicial y utilizando un conjunto de procedimientos/reglas/acciones seleccionados a priori, es capaz de explicitar el conjunto de pasos que nos llevan a una situación final que llamamos **solución**. Lo que consideremos o no solución dependerá del contexto concreto del problema, y puede ser, por ejemplo, el conjunto de acciones que nos llevan a cumplir cierta propiedad, conseguir cierto objetivo, o verificar ciertas restricciones (como hemos visto en los [CSP](../CSP.md.html)). Como estamos interesados en la generación de mecanismos automáticos que se puedan llamar inteligentes, no nos contentamos con resolver problemas individuales y dar para cada problema una solución independiente, sino que intentaremos buscar elementos comunes a una gran bolsa de problemas que faciliten dar una clasificación de los mismos y reconocer métodos y estrategias que puedan ser válidos de la forma más general posible. !!!side:1 Aunque, después, algunos sean resolubles en un tiempo razonable y otros no. Para ello, y dentro de un proceso de representación que se conoce como **modelado**, es necesario que podamos expresar las características de los problemas usando un lenguaje formal común a todos ellos para, posteriormente, proporcionar métodos y estrategias generales (en forma de algoritmos o de heurísticas, en nuestro caso) con los que se obtengan soluciones a esos problemas con ciertas garantías. Al igual que cuando dimos algoritmos de resolución de CSPs no atendimos a las particularidades de un CSP concreto, sino que intentamos dar algoritmos que pudieran ejecutarse sobre todos los CSPs definibles siguiendo la estructura/representación propuesta [1]. En este tema, nos centraremos en otro de los posibles **modelados** genéricos para formalizar un problema y sus posibles mecanismos de solución: los **espacios de estados**. Antes de definir formalmente en qué consiste esta aproximación, observemos que en todo momento estamos tratando con métodos en los que el proceso de resolución de problemas se da de forma dinámica, es decir, se supone una evolución temporal que pasa por etapas sucesivas y que nos permite ir desde la situación inicial en la que el problema se presenta hasta una situación final en la que se ha encontrado la solución del mismo: la solución se *construye* o *aproxima*. !!!def: Estado **Estado**: *representación de los elementos que describen el problema en un momento dado, es decir, a la situación en que se encuentra o se podría encontrar el problema en cada instante de tiempo de ese proceso dinámico.* !!!side:2 En un mundo ideal dispondríamos de una cantidad ilimitada de almacenamiento y con un acceso instantáneo, pero no es lo que sucede en el mundo real.  La cuestión principal que debemos plantearnos para este tipo de modelado es **qué debemos incluir en el estado**. Por desgracia, no existen directrices generales que permitan dar una respuesta satisfactoria a esta cuestión pero, siguiendo técnicas clásicas de resolución de problemas, podemos asegurar que es importante guardar un equilibrio entre el ahorro de recursos de almacenamiento para la descripción del estado y la necesidad de tener suficiente información almacenada como para poder resolver el problema. Aunque a priori puede parecer una buena idea almacenar toda la información posible, pronto veremos que en problemas relativamente pequeños la cantidad de estados puede ser tan grande que la capacidad de almacenamiento computacional se nos puede agotar sin darnos la opción de resolver el problema [2]. Vemos, pues, que este enfoque entronca directamente con teorías matemáticas bien establecidas, como son la **Teoría de la Computabilidad** (**qué** es resoluble de forma automática) y la **Teoría de la Complejidad** (**cuántos** recursos necesitamos para resolver los problemas que sí son resolubles). !!!alg Debe existir un equilibrio entre el ahorro de recursos de almacenamiento para la descripción del estado y la necesidad de tener suficiente información almacenada como para poder resolver el problema. Este proceso de elegir adecuadamente la información que almacenamos en un estado es tan importante que se ha convertido en un eje central de la Inteligencia Artificial, recibiendo el nombre de **Teoría de la Representación**, y ha demostrado ser esencial para que algoritmos y heurísticas concretas de resolución sean o no eficientes a la hora de resolver problemas. Un buen algoritmo con una mala representación puede ser tan ineficiente como un mal algoritmo y, muchas veces, una buena representación es capaz de llevarnos a una solución del problema incluso usando algoritmos malos. !!!alg La elección de los estados no solo determina qué información se almacenará de los posibles estados en los que puede estar el problema, sino que en muchos casos es determinante también para decidir cuáles son las reglas u operaciones básicas permitidas para realizar transformaciones entre estados. # Búsquedas en Espacios de Estados Si nos imaginamos este espacio de estados como un terreno por el cual nos podemos mover, donde partimos de un punto concreto del terreno (**estado inicial**) y podemos aplicar las reglas válidas para ir saltando de un estado a otro, podemos identificar la resolución del problema (llegar hasta un **estado final** válido) con la **búsqueda de un camino** (sucesión de reglas aplicadas) adecuado entre un estado inicial y un estado final. Es por ello que, muy habitualmente, se habla del **Problema de Búsqueda en el Espacio de Estados**. Pasemos pues a dar una definición formal de esta idea: !!!def:Problema de Búsqueda Básico Un **problema de búsqueda básico** es una 4-tupla $(X,S,G,T)$, donde: - $X$ es un **conjunto de estados** (el que hemos estado llamando **Espacio de Estados**). - $S \subseteq X$, es un conjunto no vacío de **estados iniciales** (puede haber muchos estados iniciales para el mismo problema). - $G \subseteq X$, es un conjunto no vacío de **estados finales** (puede haber muchos estados finales válidos para el mismo problema). - $T: X \rightarrow \cal{P}(X)$ es una **función de transición** (cada estado puede tener varios estados sucesores). !!!alg Recordamos que $\cal{P}(X)$ representa las partes de $X$, es decir, el conjunto de los posibles subconjuntos de $X$, ya que desde un estado concreto podemos llegar a varios posibles estados aplicando distintas operaciones o reglas permitidas. Observa que esta definición formal no explicita ni la forma en que hay que almacenar la información en los estados ni cuáles son las reglas válidas que permiten pasar de un estado a otro durante la resolución, ya que todo ello depende del problema concreto que se esté resolviendo. !!!note Una vez fijado este primer marco de representación, podemos dar los pasos generales necesarios para *buscar* el camino que lleve desde el estado inicial del problema hasta una solución: 1. **Dar una representación del problema**, es decir, definir un **espacio de estados** que refleje las características del mundo real que sean necesarias para la resolución del problema. Como ya se ha indicado, esta elección no es única, y determinará en gran medida la facilidad o dificultad de resolver el problema. Esta representación determina también las acciones disponibles para moverse por este espacio y las estrategias que puedan aplicarse posteriormente. 2. Especificar uno, o más, **estados iniciales**. Muchas veces se plantea como un estado aleatorio entre los posibles. 3. Especificar uno, o más **estados finales** (objetivos o metas). A veces no se especifican propiamente los estados finales, sino alguna propiedad que han de cumplir para que se consideren solución. 4. Definir **reglas** a partir de las acciones disponibles. El conjunto de reglas definirá la función de transición del sistema formal. Estas reglas determinan la estructura del espacio de estados, que es responsable, en gran medida, de la dificultad que nos encontremos posteriormente para realizar búsquedas en el espacio. 5. El problema se resuelve **usando las reglas en combinación con una estrategia de control**. De nuevo, obsérvese que aquí no prefijamos ninguna estrategia de control específica y, como hemos comentado, puede venir restringida por la representación elegida. 6. Dependiendo de la estrategia de control utilizada, o de las necesidades de la búsqueda, puede ser necesaria una **función de coste** que indique cuánto cuesta aplicar una regla determinada a un estado determinado, de esa forma podemos calcular cuánto cuesta el proceso total de ir desde un estado inicial hasta un estado final aplicando dicha estrategia, y comparar entre sí los distintos caminos que existen para resolver el problema. # Espacios como Árboles y Grafos Normalmente, los algoritmos que vamos a ver se basan en la suposición de que el espacio de búsqueda tiene la estructura de un grafo dirigido: cada **nodo** del grafo representa uno de los estados del espacio, y dos nodos están conectados si existe una forma de ir de uno al otro por medio de la función de transición. Normalmente, cuando resolvemos el problema a partir de un estado particular, podemos construir un árbol partiendo del estado inicial y añadiendo en cada nivel los estados que se pueden alcanzar desde los estados del nivel anterior (en consecuencia, puede contener estados repetidos). En este caso, la **profundidad** ($d$, de **depth**) del árbol es la longitud máxima de los caminos que conectan cualquier nodo a la raíz; y el **factor de ramificación** ($b$, de **branch**) del árbol es el máximo número de sucesores que puede tener un nodo del árbol. ![](img/State+Space+Graphs+vs.+Search+Trees.jpg width="50%") En un árbol, los sucesores inmediatos de un nodo (salvo las hojas, claro, que son los nodos terminales) se llaman **hijos**, el predecesor de un nodo (salvo la raíz, que no tiene predecesor), que es único, se llama **padre**, y los nodos que tienen el padre común se llaman **hermanos**.  Es importante destacar que nuestro espacio de estados **NO** es un árbol, sino que el árbol se consigue al considerar la estructura ordenada que surge entre los diversos estados de nuestro problema al aplicar las reglas que permiten pasar de unos estados a otros. Si cambiamos la representación de los estados (y en consecuencia las reglas que se pueden aplicar) cambiará el árbol asociado, pero nuestro problema sigue siendo el mismo. Es por ello que la representación es fundamental para obtener soluciones más o menos eficientes, ya que los posibles caminos entre los nodos que representan estados iniciales y los que representan estados finales pueden cambiar completamente dependiendo del árbol que obtengamos. # Problemas de Planificación !!!def:Problema de Planificación En muchos casos no estamos interesados *simplemente* en encontrar un estado final que verifique ciertas propiedades, sino en encontrar la sucesión de acciones-movimientos que nos llevan desde un estado inicial particular hasta un estado final deseado. En este caso estamos ante lo que se conoce como un **Problema de Planificación**, y a la sucesión concreta de acciones que resuelve el problema se le denomina **plan**. Este tipo de problemas tiene muchas aplicaciones en el mundo real: desde la robótica hasta la generación de planes para la automatización de cadenas de montaje pasando, por supuesto, en la resolución de juegos. Tal y como sucedía con los problemas de búsqueda, aquí es importante dar una representación formal del mundo y de las acciones que podemos aplicar y, si usamos la representación del mundo como espacio de estados, entonces podemos usar los algoritmos que desarrollemos para búsquedas, pero teniendo la precaución de almacenar la sucesión de acciones ejecutadas y medir las características de los caminos construidos para decidir el proceso de búsqueda en marcha. Aunque el problema de planificación general es completamente abierto y no añade restricciones al mundo ni a las acciones posibles, es habitual considerar algunas simplificaciones para poder abordarlo con ciertas garantías: - Un espacio de estados finito. - Estados completamente observables (es decir, no hay incertidumbre respecto a la situación del mundo). - Acciones deterministas (en un estado concreto, la aplicación de una acción concreta devuelve un único estado posible... no hay incertidumbre respecto al efecto de la acción). - Tiempo implícito (las acciones tardan el mismo tiempo en ejecutarse, y no afecta a la ejecución del plan). Esta es una posible aproximación a resolver problemas de planificación, pero se pueden usar aproximaciones completamente distintas, por ejemplo, haciendo uso de Lógicas. # Ejemplos ## CSPs !!!side:3 Por ejemplo, cambiar el valor de una de las variables, o rellenar alguna variable no asignada. Todos los CSPs se pueden representar como Espacios de Estados en los que los estados vienen dados por las asignaciones, y las transiciones son cambios válidos entre asignaciones [3]. ## Puzzle de piezas deslizantes !!!ejemplo: Puzzle de Piezas Deslizantes El caso general consiste en un puzzle de $n\times m$ cuadrículas, con $n\times m-1$ piezas numeradas consecutivamente y 1 hueco. El objetivo es deslizar las piezas usando el hueco hasta conseguir un orden deseado.  !!!side:4 En los bordes y esquinas sólo podrá moverse en 3 o 2 direcciones posibles, respectivamente. El espacio de estados, $X$, describe todas las posibles combinaciones de las piezas y el hueco. Como queremos dar un método general de resolución, el conjunto de estados iniciales es, en este caso, todo el espacio $S=X$, y el conjunto de estados finales es únicamente uno: el estado en el que todos están en orden y el hueco se sitúa al final, tal y como muestra la figura anterior. La función de transición describe el cambio que resulta de mover, en un estado concreto, el hueco en cualquiera de las 4 direcciones [4]. Obsérvese que, en este caso, la solución al puzzle no es el estado final, que sabemos exactamente cuál es, sino el camino que lleva desde un estado inicial (prefijado, o aleatorio) hasta ese estado final. Es decir, deseamos conocer la sucesión de movimientos que nos permiten resolver el puzzle.  En el caso de un puzzle de tamaño $3\times 3$ (que se conoce como **8-puzzle**, por el número de piezas móviles que tiene) el número de posibles estados es de $9!= 362880$, un tamaño que permite, con la capacidad de los ordenadores actuales, hacer una búsqueda exhaustiva para encontrar el camino desde cualquier estado al estado final ordenado. Esta búsqueda exhaustiva se consigue comenzando por el estado inicial e ir visitando a partir de él todos los demás estados por la aplicación sucesiva de las reglas de transición, de esta forma, si existe una solución (un camino que conecta el estado inicial y el final) este método la encontrará, aunque, posiblemente, de una forma completamente ineficiente. Si jugamos con el puzzle de tamaño $4\times 4$ (que se conoce como **15-puzzle**) el número de posibles estados es de $16! \approx 2x10^{13}$, demasiado grande para una búsqueda exhaustiva, por lo que hemos de encontrar estrategias de búsqueda más depuradas que permitan alcanzar las soluciones de forma más eficiente y usando menos recursos (en tiempo y en espacio almacenado). ## Puzzle de Misioneros y Caníbales !!!ejemplo: Puzzle de Misioneros y Caníbales Tres misioneros se perdieron explorando una jungla. Separados de sus compañeros, sin alimento y sin radio, sólo sabían que para llegar a su destino debían ir siempre hacia adelante. Los tres misioneros se detuvieron frente a un río que les bloqueaba el paso, preguntándose que podían hacer. De repente, aparecieron tres caníbales llevando un bote, pues también ellos querían cruzar el río. Ya anteriormente se habían encontrado grupos de misioneros y caníbales, y cada uno respetaba a los otros, pero sin confiar unos en otros. Los caníbales se comían a los misioneros cuando les superaban en número, y los misioneros bautizaban a los caníbales en situaciones similares. Todos querían cruzar el río, pero el bote no podía llevar más de dos personas a la vez y los misioneros no querían que los caníbales les aventajaran en número. ¿Cómo puede resolverse el problema sin que en ningún momento haya más caníbales que misioneros en cualquier orilla del río? !!!side:5 Muy descriptiva, pero poco práctica desde el punto de vista computacional. 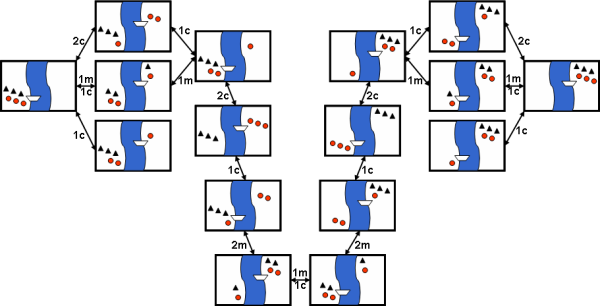El espacio de estados asociado al problema podría representarse de la siguiente forma [5]:  ## Todos los Dígitos del Rey En los casos anteriores hemos presentado problemas que tienen una representación bastante directa en Espacios de Estados. Veamos ahora un problema que ofrece una complejidad mayor para ser resuelto de la misma forma: !!!ejemplo: Todos los Dígitos del Rey Dado el conjunto de dígitos $\{0,\dots,9\}$, insertar los símbolos de los operadores aritméticos ($\times + - /,$) entre ellos para que la expresión resultante se evalúe como 100. Por ejemplo: \[0+1+2+3+4+5+6+7+(8\times 9) =100\] # Evaluación y Rendimiento Antes de que pasemos a ver la variedad de algoritmos (estrategias) que han sido diseñados para resolver problemas de búsqueda en espacios de estados, puede merecer la pena mencionar, aunque sea de forma breve, cómo podemos evaluar la eficiencia de estos algoritmos. !!!note Habitualmente, se suelen usar los siguientes criterios de evaluación para evaluar el rendimiento de los algoritmos existentes: - **Complejidad en tiempo**: Se puede medir como el número de veces que se aplica la función de transición para encontrar la solución. En un contexto más amplio suele medirse por medio del número de pasos que da un algoritmo en su ejecución. En algunos problemas a cada transición se le asigna un coste personalizado y el coste en tiempo se calcula como la suma de las transiciones aplicadas. - **Complejidad en espacio**: Se mide por la cantidad de espacio de almacenamiento necesario para encontrar la solución. En el caso que estamos viendo lo podemos medir como el número de estados que el algoritmo debe mantener en memoria para encontrar la solución. Algunos algoritmos podrán *olvidar* los estados por los que van pasando, mientras que otros necesitan mantener una memoria con esos estados para poder volver atrás en la búsqueda o saber por cuáles ha pasado. - **Completitud**: Si existe una solución, ¿está garantizado por el algoritmo que la encontraremos? - **Optimalidad**: Si existen varias soluciones, ¿encuentra el algoritmo la óptima? Esta optimalidad se mide respecto de alguna medida, por ejemplo, número de acciones para encontrar la solución, o cantidad de memoria usada. (insert ../menu.md.html here)