**Fractales**
El matemático **Benoît Mandelbrot** fue el responsable de introducir, en el año 1975, el concepto de **fractal**, que proviene del vocablo latino **fractus** (que puede traducirse como *quebrado*). El término acuñado por el francés pronto fue aceptado por la comunidad científica e incluso ya forma parte del diccionario de la Real Academia Española.
Desde el punto de vista más habitual, un **fractal** es un objeto matemático, habitualmente geométrico, cuya principal característica es que su apariencia y la manera en que se distribuye estadísticamente no varía aun cuando se modifique la escala empleada en la observación.
Si bien el término fractal es reciente, los objetos hoy denominados fractales eran bien conocidos en matemáticas desde principios del siglo XX. Las maneras más comunes de determinar lo que hoy denominamos dimensión fractal fueron establecidas a principios del siglo XX en el seno de la teoría de la medida.
Los fractales son, por lo tanto, elementos calificados como semi geométricos (por su irregularidad no pertenecen a la geometría tradicional) que disponen de una estructura esencial que se reitera a distintas escalas. El fractal puede ser creado por el hombre, incluso con intenciones artísticas, aunque también existen estructuras naturales que son fractales (como los copos de nieve).
!!!note
De acuerdo a Mandelbrot, los fractales pueden presentar 3 clases diferentes de autosimilitud, lo que significa que las partes tienen la misma estructura que el conjunto total:
* **autosimilitud exacta**, el fractal resulta idéntico a diferentes escalaa;
* **cuasiautosimilitud**, con el cambio de escala, las copias del conjunto son muy semejantes, pero no idénticas;
* **autosimilitud estadística**, Solo se conservan algunas propiedades estadísticas durante el cambio de escala, no el propio conjunto de puntos.
!!!side:1
Se utiliza, principalmente, para la compresión de imágenes.
Las técnicas fractales se utilizan, por ejemplo, para comprimir datos. A través del **Teorema del Collage**, es posible encontrar un **IFS** (**Sistema de funciones Iteradas**) que se aproxima al objeto final que queremos comprimir. De esta forma, podemos sustituir el objeto original por el IFS que, normalmente, ocupará mucha menos memoria [1].
# La dimensión fractal
La geometría clásica no es lo suficientemente amplia como para abarcar los conceptos necesarios para medir las diferentes formas fractales. Si tenemos en cuenta que se tratan de elementos cuyo tamaño cambia incesantemente no es fácil, por ejemplo, calcular su longitud. La razón es que si se intenta realizar una medición de una línea fractal utilizando una unidad tradicional, existirán siempre componentes tan pequeños y delgados que no podrán ser delimitados con precisión.

En la curva de Koch (en la imagen de la derecha se muestran 3 de estas curvas para formar lo que se conoce como **copo de nieve**), se aprecia que desde su nacimiento crece a cada paso un tercio a lo largo; en otras palabras, la longitud de la porción que se ubica al principio se incrementa sin fin, determinando que cada curva sea 4/3 de la precedente.
Dado que la longitud de la línea fractal y la del instrumento de medición o la unidad de medida escogida están directamente relacionadas, resulta absurdo utilizar dicha noción. Es por eso que se ha creado el concepto de dimensión fractal que permite, cuando hablamos de líneas fractales, conocer de qué manera o en qué grado ocupan una porción de plano.
En relación con la geometría tradicional, un segmento posee dimensión uno, un círculo, dos, y una esfera, tres. Dado que una línea fractal no abarca toda la porción de plano, debería tener una dimensión que no llegue a dos.
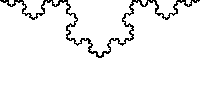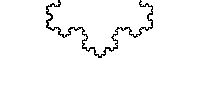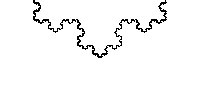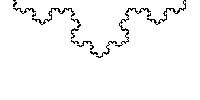
Puedes ver cálculos específicos de dimensión de objetos fractales en este [documento de Miguel Reyes](./images/2015-11/fractales.pdf).
# Aplicaciones de los fractales
Se han utilizado técnicas de fractales en la compresión de datos y en diversas disciplinas científicas.
## Compresión de imágenes
Comprimir la imagen de un objeto autosemejante como el helecho de la figura no es difícil: haciendo uso del [teorema del collage](http://es.wikipedia.org/wiki/Sistema_de_funciones_iteradas#El_problema_inverso:_Teorema_del_collage), debemos encontrar un IFS, conjunto de transformaciones que lleva la figura completa (en negro) en cada una de sus partes autosemejantes (rojo, azul celeste y azul marino). La información sobre la imagen quedará codificada en el IFS, y la aplicación reiterada de dichas transformaciones permite obtener la imagen procesada en cuestión.
Pero el enfoque anterior plantea problemas con muchas imágenes reales: no esperamos, por ejemplo, que la imagen de un gato presente pequeños gatitos distorsionados sobre sí mismo. Para solventarlo, en 1989 Arnaud Jacquin creó el esquema de sistemas de funciones iteradas particionadas: en él se subdivide la imagen mediante una partición y para cada región resultante se busca otra región similar a la primera bajo las transformaciones apropiadas.
El esquema resultante es un sistema de compresión con pérdidas, de tiempo asimétrico. Lamentablemente aún se tarda mucho en encontrar las transformaciones que definen la imagen. No obstante, una vez encontradas, la descodificación es muy rápida. La compresión, aunque dependa de muchos factores, suele ser equiparable a la compresión JPEG, con lo cual el factor tiempo resulta determinante para decantarse por uno u otro sistema.
## Modelado de formas naturales
Las formas fractales, las formas en la que las partes se asemejan al todo, están presentes en la materia biológica, junto con las simetrías (las formas básicas que solo necesitan la mitad de información genética) y las espirales (las formas de crecimiento y desarrollo de la forma básica hacia la ocupación de un mayor espacio), como las formas más sofisticadas en el desarrollo evolutivo de la materia biológica en cuanto que se presentan en procesos en los que se producen saltos cualitativos en las formas biológicas, es decir posibilitan catástrofes (hechos extraordinarios) que dan lugar a nuevas realidades más complejas, como las hojas que presentan una morfología similar a la pequeña rama de la que forman parte que, a su vez, presentan una forma similar a la rama, que a su vez es similar a la forma del árbol, y sin embargo cualitativamente no es lo mismo una hoja (forma biológica simple), que una rama o un árbol (forma biológica compleja).
## Sistemas dinámicos
Pero además las formas fractales no sólo se presentan en las formas espaciales de los objetos sino que se observan en la propia dinámica evolutiva de los sistemas complejos. Dinámica que consta de ciclos (en los que partiendo de una realidad establecida simple acaban en la creación de una nueva realidad más compleja) que a su vez forman parte de ciclos más complejos los cuales forman parte del desarrollo de la dinámica de otro gran ciclo. Las evoluciones dinámicas de todos estos ciclos presentan las similitudes propias de los sistemas caóticos.
## En manifestaciones artísticas
Se usan tanto en la composición armónica y rítmica de una melodía como en la síntesis de sonidos. Esto se debe al uso de lo que en composición se llaman *micromodos*, o pequeños grupos de 3 notas, a partir de los cuales uno puede trabajarlos de manera horizontal (melódica), o vertical (armónica). A su vez, el ritmo puede ser trabajado en sucesiones temporales específicas, que son determinadas por sucesiones de fractales.
Maurits Cornelis Escher (1898-1972), fue un artista holandés. Sus litografías grabados han ilustrado muchísimas páginas de libros. Se desconoce si alguna vez llegó Escher a manejar el término *Fractal* pero es cierto que desarrolló con frecuencia estructuras matemáticas complejas y avanzadas mientras continuaba pregonando su desconocimiento total con la materia.
Con programas informáticos como [Apophysis](http://es.wikipedia.org/wiki/Apophysis) se pueden hacer imágenes a partir de fractales con técnicas diversas: cambiando parámetros, geometría de triángulos o con transformaciones aleatorias.
## Fractal AI
Recientemente, y haciendo uso de conceptos relacionados con Teoría de la Información, Sergio Hernández ha propuesto el uso de fractales para dar una versión mejorada del uso de la Entropía como base motora del proceso de inteligencia, pasando del concepto de **Inteligencia Artificial Entrópica** al de **Inteligencia Artificial Fractal**. En su [blog](http://entropicai.blogspot.com.es/) se pueden encontrar ejemplos muy interesantes de cómo usar este tipo de soluciones para optimizar el comportamiento de sistemas dinámicos (usualmente agentes) hacia direcciones en las que habitualmente reconoceríamos inteligencia.
(insert menu.md.html here)