**Introducción a Prover9 y Mace4**
!!!side:1
William Walker McCune (17 de diciembre de 1953 - 2 de mayo de 2011) fue un informático y lógico estadounidense que trabajó en los campos del razonamiento automatizado, el álgebra, la lógica y los métodos formales. En 2000, McCune recibió el Premio Herbrand por su destacada contribución al razonamiento automatizado[1]. En 2013, se publicó en su honor Automated Reasoning and Mathematics - Essays in Memory of William W. McCune.
 **[Prover9](http://www.cs.unm.edu/~mccune/prover9/)** es un demostrador automático de teoremas para [Lógicas de Primer Orden](De_Resolucion_LP_a_LPO.md.html) (también se puede utilizar con [Lógica Proposicional](Curso_acelerado_LP.md.html)) y **Mace4** busca modelos finitos y contraejemplos. Ambos fueron desarrrollados por William McCune, y se pueden usar por medio de un interfaz gráfico unificado, para aprovechar el uso conjunto que se suele hacer de ambas herramientas en la resolución de problemas. Prover9 es un sucesor de **Otter**, un demostrador automático también creado por McCune.
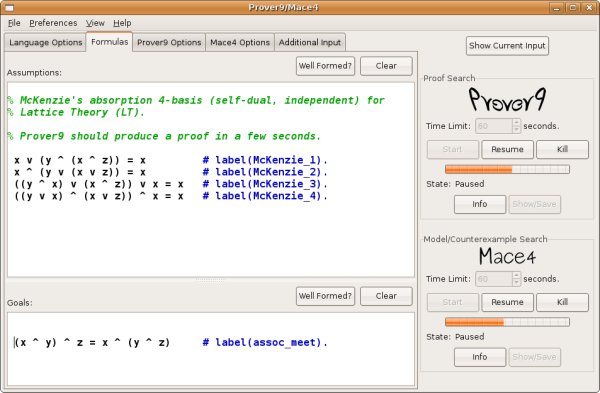
Ambos siguen la misma interfaz común, por lo que la sintaxis que usan es la misma. La siguiente tabla muestra el formato (de texto) que se debe usar para ello:

En la pestaña **Formulas** debemos introducir las fórmulas que definen el problema que queremos resolver, y ofrece dos cajas de texto claramente diferenciadas para ello:
* en la caja **Assumptions** se introducen las hipótesis.
* en la caja **Goals** se introduce la fórmula que queremos probar.
!!!side:2
Que se puede personalizar por medio de la pestaña **Prover9 Options**, y también a través de directivas en el fichero de entrada.
Aunque admite una forma de trabajo guiada [2], nosotros haremos uso esencialmente del modo completamente automático que trae, en el que Prover9 sigue el siguiente protocolo:
* El modo principal de inferencia usado por Prover9 es el de **resolución**, aplicando iteradamente resolventes simples con el fin de llegar a detectar una **inconsistencia**.
!!!side:3
Y que se corresponen con preprocesamientos comunes a muchos métodos de inferencia.
* Para poder aplicar el método de resolución, Prover9 comienza realizando algunos **preprocesamientos** en las fórmulas de entrada para convertirlas en las forma necesaria para realizar las inferencias [3]:
1. Primero **niega la fórmula objetivo**.
2. Entonces **traslada todas las fórmulas a forma clausal**.
3. En algunos casos hace algunos preprocesamientos adicionales, pero no son esenciales para lo que vamos a explicar aquí.
!!!side:4
Salvo en casos muy simples, el número de inferencias a realizar puede ser extremadamente alto.
* A partir de aquí, realizará una sucesión de inferencias por resolución con el fin de llegar a alguna conclusión acerca del problema propuesto [4].
* Si detecta una inconsistencia, para y devuelve una prueba formada por la secuencia de resoluciones que han generado esa inconsistencia, así como algunas estadísticas asociadas a la prueba encontrada.
La siguiente ventana muestra un ejemplo sencillo proposicional en el que se busca si es cierto que:
$$\{p\wedge s,\ p\rightarrow q,\ q\rightarrow r\} \models r\vee t$$

Y la prueba que Prover9 ofrece tras pulsar el botón **Start**:

Un ejemplo similar en Primer Orden se muestra en las siguientes figuras, donde se resuelve el problema:
$$\{\forall x (hombre(x)\rightarrow mortal(x)),\ hombre(socrates)\}\models mortal(socrates)$$
 
Prover9 intenta demostrar que \(\Sigma \models \varphi\) intentando probar que \(\Sigma \cup \{\neg \varphi\}\) no es satisfactible. Pero, ¿qué ocurre si Prover9 falla en este intento?, en ese caso, es posible que \(\Sigma \cup \{\neg \varphi\}\) sea satisfactible y lo ideal sería obtener un modelo que lo satisface, y ese es el papel que juega Mace4.
!!!side:5
Los elementos de ese universo se denotarán siempe como \(\{0,\ 1,\ \dots,\ n-1\}\) para un conjunto de tamaño \(n\).
Mace4 busca únicamente estructuras finitas sin orden, es decir, un modelo que tiene como universo un conjunto finito [5], y un conjunto de funciones y relaciones (en forma de tabla) sobre el universo, que se identifican con los símbolos de funciones y predicados que se dan en la especificación de las fórmulas introducidas. Debe notarse que solo busca **modelos finitos** para conjuntos de fórmulas de primer orden, aunque lo podremos utilizar para la Lógica Proposicional, considerando que los Lenguajes de Primer Orden son una extensión de ella.
El método que sigue Mace4 es:
* Para un dominio de un tamaño prefijado, se construyen todas las intancias de todas las fómrulas para ese dominio. el resultado es un conjunto de cláusulas base con igualdad.
* Entonces, se aplica un procedimiento basado en reescritura ecuacional de base y, si se detecta satisfacibilidad, se muestra el modelo (o modelos) encontrado(s).
Por defecto, Mace4 comienza buscando una estructura de tamaño 2 y va incrementando el tamaño de búsqueda hasta que encuentra un modelo o alcanza cierto límite prefijado.
En el siguiente ejemplo proposicional intentamos ver si es cierto que:
$$\{p\wedge s,\ p\rightarrow q,\ q\rightarrow r\} \models r\wedge t$$
Prover9, tras un breve tiempo de búsqueda (porque intervienen muy pocas variables) indica que ha terminado la búsqueda sin éxito, es decir, que no ha encontrado una inconsistencia. Lo que nos lleva a usar Mace4 para buscar un contramodelo de:
$$\{p\wedge s,\ p\rightarrow q,\ q\rightarrow r,\ \neg(r\wedge t)\}$$
Tras la ejecución de Mace4 obtenemos el siguente modelo (contraejemplo de la consecuencia buscada):

La figura izquierda muestra la salida directa de Mace4, mientras que la derecha muestra el resultado de usar la opción de reformateo que ofrece el programa para mostrar el modelo de forma **tabular**, donde es más fácil interpretar los resultados y entender por qué falla.
Veamos un ejemplo de búsqueda de contramodelos en LPO. Para ello consideremos el siguiente problema:
$$\{\forall x \exists y (R(x,y))\}\models \exists y \forall x (R(x,y))$$

De nuevo, si lo intentamos con Prover9, el sistema es incapaz de dar una demostración (no encuentra una inconsistencia) debido a que es falso. Así pues, usamos Mace4 para encontrar un contraejemplo (un modelo donde \(\forall x \exists y (R(x,y))\) es cierto, pero no se verifica \(\exists y \forall x (R(x,y))\)). La ejecución de Mace4 propone el siguiente contramodelo:
 
Tal y como hicimos en el caso proposicional, la figura de la izquierda muestra la salida directa de Mace4, mientras que la de la derecha muestra el resultado de reformatear el modelo obtenido usando la opción **cooked**. En este caso, nos propociona un modelo con un universo formado por dos elementos \(\{0,1\}\), y una interpretación de \(R\) como: \(\{(0,0),\ (1,1)\}\) (es decir, \(R\) se verifica en esos dos pares, pero no en los pares \((0,1)\) y \((1,0)\)).
(insert menu.md.html here)