**Introducción a la Lógica Difusa**
La forma en que la gente piensa es, inherentemente, difusa. La forma en que percibimos el mundo está cambiando continuamente y no siempre se puede definir en términos de sentencias completamente verdaderas o falsas.
Consideremos como ejemplo el conjunto de vasos del mundo, que pueden estar vacíos o llenos de agua. Ahora tomemos un vaso vacío y comencemos a echar agua poco a poco, ¿en qué momento decidimos que el vaso pasa de estar vacío a estar lleno? Evidentemente, hay dos situaciones extremas que reconocemos sin ninguna duda, la primera cuando el vaso está completamente vacío, sin una sola gota de agua en su interior, y la segunda cuando está completamente lleno, cuando no cabe ni una sola gota más en él, pero una gota antes de estar completamente lleno, ¿diríamos que es falso que el vaso está lleno?, observa que para afirmar su condición, en la frase anterior no solo he usado el término **lleno**, sino que he añadido un modificador diciendo **completamente lleno**. Si a un vaso lleno de agua le quito una gota de agua... ¿dejo de considerarlo lleno y automáticamente pertenece para mí a otra clasificación?
Las definiciones de **vaso completamente vacío** y **vaso completamente lleno** son demasiado estrictas como para que resulten interesantes en un razonamiento en el que se consideran operaciones de llenado y vaciado de vasos, y entre los términos de **lleno** y **vacío** hay un área que no está claramente definida de pertenencia absoluta a ninguno de esos extremos. En el lenguaje natural que usamos en el mundo real hemos cubierto esta imprecisión por medio de una jerarquía de términos intermedios junto con modificadores que permiten cubrir un espectro más grande de áreas usando un número limitado de ellos, y podemos hablar de lleno, medio lleno, completamente lleno, casi lleno, etc.
!!!side:1
Si consideramos el conjunto de los vasos llenos, un nuevo vaso estará lleno si pertenece o no a este conjunto.
Matemáticamente, los conceptos de **sí/no**, **verdadero/falso** están representados por medio del concepto clásico de conjunto [1], pero necesitamos extenderlo para poder representar este tipo de información más difusa.
Frente al concepto tradicional de conjunto, en el que un elemento está o no está, no hay términos intermedios, un **conjunto difuso** permite a sus elementos tener un grado de pertenencia. Si el valor 1 se asigna a los elementos que están completamente en el conjunto, y 0 a los que están completamente fuera, entonces los objetos que están parcialmente en el conjunto tendrán un valor de pertenencia estrictamente entre 0 y 1. Por tanto, si un vaso completamente lleno tiene un grado de pertenencia a **los vasos llenos** de valor 1, y un vaso completamente vacío un grado de pertenencia a **los vasos llenos** de valor 0, entonces al añadir una gota a este último, su grado de pertenencia **a los vasos llenos** sería ligeramente superior a 0.
# Conjuntos Difusos
Matemáticamente, un conjunto es una colección de objetos que verifican alguna propiedad, de forma que un objeto o bien pertenece al conjunto, o no pertenece. Por ejemplo, supongamos que decimos que una persona es alta si su altura está por encima de 180cm, algo que puede ser representado gráficamente de la siguiente forma:
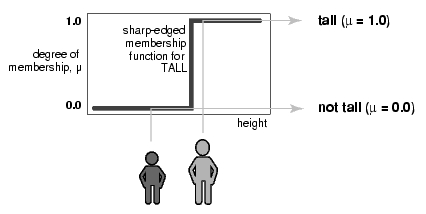
La función anterior describe la pertenencia al **conjunto de los altos**, o estás dentro o estás fuera. Estas funciones **nítidas** funcionan muy bien con las operaciones matemáticas clásicas, pero no funcionan tan bien describiendo el mundo real. Por una parte, no hace distinción entre individuos que midan 181cm y los que miden 215cm, aunque hay una clara distinción entre ellos. El otro problema es la diferencia entre una persona que mida 180cm y otra de 181cm, apenas 1cm de diferencia entre ellos y el primero de ellos no está en el conjunto de los altos, y el segundo sí.
La aproximación de los conjuntos difusos al conjunto de los altos proporciona una representación mucho mejor sobre la propiedad **ser alto** de una persona. El conjunto se define por medio de una función continua que puede tomar valores intermedios entre los extremos 0 y 1.
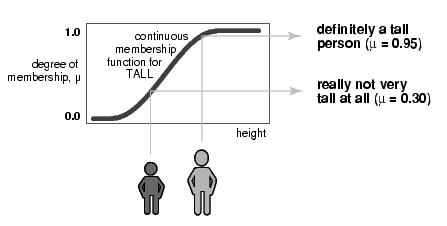
La función de pertenencia define el conjunto difuso para los posibles valores de altura (mostrados en el eje horizontal) y proporciona el grado de pertenencia de la altura al conjunto difuso (mostrado en el eje vertical con valores entre 0 y 1). De esta forma, siguiendo la figura anterior, el grado de pertenencia de la primera persona es 0.3 y, por tanto, no es muy alto, mientras que el segundo tiene un grado de pertenencia de 0.95 y, definitivamente, es alto.
!!!side:2
L.A. Zadeh, *Fuzzy sets*, Information and Control, Volume 8, Issue 3, 1965, Pages 338-353, ISSN 0019-9958, [https://doi.org/10.1016/S0019-9958(65)90241-X](https://www.sciencedirect.com/science/article/pii/S001999586590241X)
**Abstract**: A fuzzy set is a class of objects with a continuum of grades of membership. Such a set is characterized by a membership (characteristic) function which assigns to each object a grade of membership ranging between zero and one. The notions of inclusion, union, intersection, complement, relation, convexity, etc., are extended to such sets, and various properties of these notions in the context of fuzzy sets are established. In particular, a separation theorem for convex fuzzy sets is proved without requiring that the fuzzy sets be disjoint.
Los **conjuntos difusos** fueron propuestos inicialmente por Lofti A. Zadeh en su artículo de 1965 titulado _Fuzzy Sets_ [2]. Este artículo establece los fundamentos de la Lógica Difusa que se deduce de la definición de conjunto difuso y sus propiedades. Esta definición es:
!!!def:Conjuntos Difusos
Sea $X$ un conjunto clásico. Un conjunto difuso, $A$, en $X$ viene caracterizado por la función de pertenencia $f_A(x)$, que asocia a cada punto $x \in X$ un número real del intervalo $[0,1]$, donde los valores de $f_A(x)$ representan el *grado de pertenencia* de $x$ en $A$, de forma que, cuanto más cerca esté el valor de $f_A(x)$ a $1$, mayor es el grado de pertenencia de $x$ a $A$.
!!!side:3
Obsérvese que no indicamos cómo ha de ser la función de pertenencia, ya que eso dependerá de las características propias del conjunto real que se quiere representar, pero suelen usarse algunas funciones clásicas comunes como las que se muestran a continuación:

Esta definición de conjunto difuso extiende de alguna forma la definición clásica de conjunto, que sería el caso particular en el que $f_A(x)\in \{0,1\}$. Pero para trabajar con ellos también tendremos que extender las operaciones clásicas entre conjuntos (unión, intersección, etc.), lo que nos llevará a extender las operaciones lógicas binarias habituales (conjunción, disyunción, etc.) [3].
# Matizadores Lingüísticos
Antes de pasar a las definiciones formales de las operaciones binarias habituales, veamos cómo esta aproximación también permite dar una representación matemática de los modificadores lingüísticos a los que hacíamos mención en la introducción.
El primer paso para convertir el lenguaje difuso en una función de pertenencia de la Lógica Difusa consiste en tomar los términos (normalmente adjetivos o expresiones que indican propiedades) y asociarles una función de pertenencia adecuada a nuestra experiencia del mundo real. Aquí no hay reglas fijas, salvo las restricciones propias de la lógica.
El siguente paso es elegir cómo actúan los matizadores lingüísticos sobre el lenguaje. Estos matizadores deben modificar la función de pertenencia de la propiedad sobre la que actúan, de forma que podamos reflejar adecuadamente las acciones de términos como *mucho*, *muy*, *casi*, *ligeramente*, *extremadamente*, *muchísimo*, etc...
Normalmente, lo que se hace es tomar la familia de funciones de la forma:
$$h_\alpha(x)=x^\alpha$$
y se asocian valores concretos de $\alpha$ a los distintos matizadores. Por ejemplo:
$$\alpha(muy)=2$$
$$\alpha(extremadamente)=6$$
$$\alpha(ligeramente)=\frac{1}{2}$$
Así, si queremos modificar el comportamiento de la función de pertenencia *alto* para obtener *muy alto*, basta considerar:
$$f_{muy\ alto}(x)=h_{muy}(f_{alto}(x))$$
# Operaciones Lógicas Difusas
!!!side:4
Por ejemplo:
$$A \cup B =\{x:\ x\in A \vee x\in B\}$$
$$A \cap B =\{x:\ x\in A \wedge x\in B\}$$
$$A^c =\{x:\ \neg(x\in A) \}$$
La lógica tradicional bivaluada usa los operadores booleanos $\wedge$ (AND), $\vee$ (OR), y $\neg$ (NOT) para convertir las operaciones de conjuntos de intersección, unión y complementario en operadores sobre los predicados de pertenencia [4]. Estos operadores funcionan bien con conjuntos nítidos, clásicos, y se pueden definir sencillamente a partir de las funciones de verdad asociadas a cada operador (normalmente, estas funciones se representan por medio de lo que se conoce como Tablas de Verdad).
Estas tablas de verdad funcionan bien para la lógica bivaluada pero, debido a que los conjuntos difusos no tienen por qué tomar una cantidad finita de valores, no es fácil extender las tablas para su uso en este caso. Estos operadores necesitan ser redefinidos como funciones para todos los posibles valores difusos de los grados de pertenencia, es decir, para todo el intervalo $[0,1]$, y no solo para los valores extremos. La Lógica Difusa es realmente un superconjuto de la lógica clásica ya que incluye los valores extremos (donde se espera que funcione igual que la clásica) junto a todos los valores intermedios, por lo que conseguir una forma generalizada de estos operadores que extiendan a los operadores clásicos puede ser de mucha utilidad. Una posible generalización vendría dada por:
$$x\ \wedge \ y = min(x,y)$$
$$x\ \vee \ y = max(x,y)$$
$$\neg \ x = 1 - x$$
Estas definiciones se pueden usar tanto para aplicar los operadores clásicos como para obtener combinaciones difusas. Las siguientes gráficas representan el resultado obtenido con las definiciones anteriores sobre todos los posibles valores de entrada:
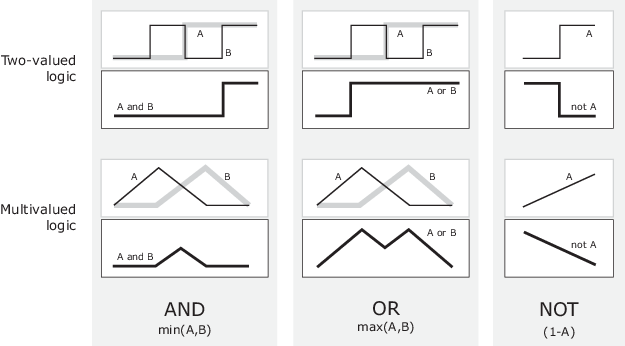
Existen muchas otras definiciones alternativas para estos operadores, pero todas ellas suelen compartir propiedades similares (que extienden el funcionamiento y significado clásico):
1. La definición matemática más general del operador AND se llama **norma triangular** (o **t-norma**) y es, por definición, un operador binario, definido de $[0,1]^2 \mapsto [0,1]$, conmutativo, asociativo, que lleva el par $(1,1)$ al valor $1$, y es creciente en cada variable.
2. Para el operador OR las propiedades son las mismas, salvo que lleva el par $(0,0)$ al valor $0$, y se llama **t-conorma**.
3. El operador NOT puede ser redefinido siempre y cuando sea continuo y estrictamente decreciente.
La siguiente figura muestra algunos ejemplos alternativos de definición:
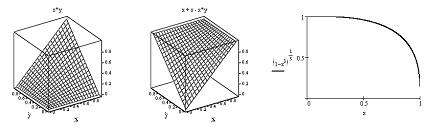
# Reglas Difusas
La mayoría de las decisiones que la gente toma son decisiones lógicas, miran la situación, la valoran, y toman una decisión basándose en ella. La forma generalizada de una decisión de este tipo se llama **Modus Ponens Generalizado**, que tiene la forma:
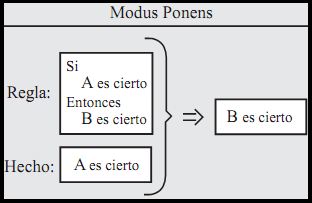
Esta forma de razonamiento lógico es bastante estricto, y pocas veces en la vida real podemos afirmar que las condiciones expresadas son totalmente ciertas o totalmente falsas. La Lógica Difusa pierde esta forma estricta diciendo que B se dará con más opciones si la veracidad de A es más alta, donde ahora A y B toman valores difusos. El razonamiento anterior requiere que se defina un conjunto de reglas que lo lleven a cabo. Estas reglas son reglas lingüísticas que relacionan diferentes conjuntos y valores difusos. La forma general de estas reglas es: *si $x$ está en $A$, entonces $y$ está en $B$*, donde $x$ e $y$ son valores difusos en los conjuntos difusos $A$ y $B$, respectivamente (y que vendrán definidos por medio de sus funciones de pertenencia).
!!!side:5
Sabri, N., Aljunid, S. A., Salim, M. S., Badlishah, R. B., Kamaruddin, R., & Malek, M. A. (2013). Fuzzy inference system: Short review and design. Int. Rev. Autom. Control, 6(4), 441-449.
Las reglas lingüísticas se usan para relacionar las entradas con las salidas, pero hemos de ver cómo se puede hacer una valoración correcta de ellas siguiendo un cálculo fiable y verificado. Ha habido varias propuestas para determinar la ejecución de estas reglas, las más importantes han sido los métodos de inferencia y agregación de Mamdani, Larsen, Takagi-Sugeno-Kang, y Tsukamoto [5].
Desde un punto de vista práctico se usan fundamentalmente dos métodos para modelar la implicación, uno de ellas es por medio del **mínimo** (que **trunca** la función de pertenencia del consecuente con el valor del antecedente), y el otro por medio del **producto** (que **escala** la función del consecuente de acuerdo al antecedente).
Las figuras siguientes muestran la aplicación de estos métodos sobre las mismas reglas con los mismos valores, donde la gráfica verde muestra el resultado de la implicación superpuesta al conjunto borroso de la consecuencia, para que se vea claramente el efecto obtenido:
# Sistema de Razonamiento Difuso
Desde un punto de vista práctico, los pasos que hay que seguir son:
1. Aprender a pasar de los conceptos lingüísticos difusos a variables numéricas difusas.
2. Combinarlas usando los operadores lógicos difusos.
3. Obtener la deducción de cada regla de forma numérica.
4. Agregar las diversas respuestas de las distintas reglas.
4. Volver a pasar de la respuesta numérica agregada a la lingüística.
!!!side:6
Extraído de [Fuzzy Logic for Social Simulation using NetLogo](http://luis.izqui.org/papers/Izquierdo_et_al_2015.pdf).
En la siguiente figura se muestra el proceso completo sobre una base de 3 reglas (a continuación analizaremos en detalle sobre el mismo ejemplo cómo es el proceso completo) [6]:
* R1: **SI** (House is Inexpensive OR Close-to-work), **ENTONCES** Suitability is Good.
* R2: **SI** (House is Expensive OR Far-from-work), **ENTONCES** Suitability is Low.
* R3: **SI** (House is Averagely-priced AND About-50-km-from-work), **ENTONCES** Suitability is Regular.

!!!side:7-8
[7] A los conjuntos difusos también se les llama en español conjuntos borrosos, pero en español no hay palabras adecuadas para el proceso de aumentar el carácter de *borroso* de algo.
[8] O por algún método automático de extracción de reglas a partir de una casuística almacenada.
En general, el proceso mostrado anteriormente responde a un esquema de modelado que permite manipular reglas de inferencia sobre conjuntos difusos, y que puede ser resumido de la siguiente forma:

* **Fuzzyficador**: convierte las entradas del sistema, que son valores numéricos nítidos en conjuntos borrosos aplicando una función de borrosificación [7].
* **Base de conocimiento (Reglas Difusas)**: almacena las reglas **SI-ENTONCES** obtenidas de los expertos [8].
* **Motor de inferencia**: simula el razonamiento humano haciendo inferencia sobre las entradas recibidas y las reglas **SI-ENTONCES** almecenadas.
* **Desfuzzyficador**: convierte el conjunto borroso obtenido por el motor de inferencia en un valor numérico nítido que puede ser reutilizado.
!!!side:9
Es el mismo ejemplo que se muestra en la figura inicial de esta sección.
El procedimiento de razonamiento difuso lo explicaremos ilustrándolo por medio de un problema sencillo y concreto extraído del tutorial de la extensión de [Lógica Difusa existente para NetLogo](https://github.com/luis-r-izquierdo/netlogo-fuzzy-logic-extension/releases), que trata sobre la adecuación de alquilar una vivienda dependiendo del precio y la distancia al trabajo [9].
En concreto, supondremos tres apreciaciones difusas respecto al precio de una vivienda: **barato**, **caro**, o **precio medio**; y otras tres apreciaciones difusas respecto a la distancia que tiene la vivienda a nuestro lugar de trabajo: **cerca**, **lejos** o **alrededor de 50Km**. Como resultado, queremos valorar la vivienda como: **muy adecuada**, **poco adecuada**, o **medianamente adecuada**. Además, los expertos (en este caso, nosotros mismos) identifican tres reglas difusas que pueden ayudarnos a tomar la decisión en función de las características de las viviendas que encontramos:
* Si la vivienda es barata o está cerca del trabajo, entonces es muy adecuada.
* Si la vivienda es cara o está lejos del trabajo, entonces es poco adecuada.
* Si la vivienda es de precio medio y está alrededor de 50Kms del trabajo, entonces es medianamente adecuada.
!!!side:10
Usando la extensión anterior en NetLogo podemos definir las condiciones de las variables de la siguiente forma:

Supondremos que el precio se puede mover entre 0 y 200€ por semana, y las viviendas han sido consideradas a una distancia máxima de 100Kms. La adecuación la vamos a valorar entre 0 y 10. Vamos a suponer que los conjuntos difusos relacionados con el precio siguen funciones lineales a trozos, mientras que aquellos asociados a la distancia y la adecuación se modelan con funciones gaussianas [10], tal y como muestra la siguiente figura:

Nuestro objetivo es usar Lógica Difusa para extraer un valor de adecuación para cada casa que valoremos, y de esa forma poder comparar mejor las diversas opciones que hay a nuestro alcance. De cada vivienda a evaluar obtenemos dos valores numéricos que corresponden al **precio** y **distancia** a la que se encuentra. El proceso que se sigue es el siguiente:
1. **Convertir en borroso** (codificación) los datos de entrada.
2. Para cada regla, **evaluar el antecedente de la regla sobre los datos de entrada**: basta aplicar el método del operador lógico que interviene en el antecedente sobre los valores borrosos de los datos de entrada obtenidos en el apartado anterior.
3. **Obtener la conclusión de la regla borrosa aplicada**: basta aplicar el operador asociado a la implicación lógica sobre el resultado del antecedente, y considerar el conjunto difuso asociado a la conclusión de la regla.
!!!side:11
Debe tenerse en cuenta que aquí se obtiene un conjunto difuso, no un valor.
4. **Agregar las conclusiones de todas las reglas consideradas**: lo que produce un nuevo conjunto borroso, aplicando la función de agregación seleccionada para agregar todas las reglas de nuestro sistema [11]. Los operadores más comunes de agregación son el máximo, la suma, o el equivalente al OR visto anteriormente.
!!!side:12
La extensión de NetLogo implementa algunos de ellos: First of Maxima, Last of Maxima, Middle of Maxima, Mean of Maxima, Centro de Gravedad.
5. **Decodificación del nuevo conjunto (agregado) borroso obtenido**: aplicando el tipo de desfuzzyficación deseado se obtiene un valor numérico que indica la adecuación de la vivienda concreta que estamos evaluando. Para ello hay muchos [métodos habituales](https://en.wikipedia.org/wiki/Defuzzification) (y ningún mecanismo para saber cuál es el que más conviene) [12].
!!!side:13
El código de NetLogo que resuelve el ejemplo que estamos desarrollando sería:

La siguiente figura muestra una interfaz de trabajo que permite seleccionar las funciones que implementan los operadores lógicos, de implicación, agregación y desborrificación [13]:

# ¿Por qué usarlos?
A la hora de decidir si usar un Sistema de Razonamiento Difuso hemos de tener en cuenta algunas consideraciones adicionales que quizás nos ayuden a decidir de forma adecuada:
* La Lógica Difusa **no resuelve problemas nuevos**, sino que utiliza nuevos métodos para resolver los problemas de siempre.
* **Los conceptos matemáticos** dentro del razonamiento difuso **son muy simples** y se pueden implementar con relativa facilidad.
* La Lógica Difusa es **flexible**: es fácil transformar un sistema difuso añadiendo o eliminando reglas sin tener que empezar desde cero.
* La Lógica Difusa **admite datos imprecisos** (pero cuidado, no estudia la incertidumbre): maneja elementos de un conjunto borroso, es decir, valores de una función de pertenencia. Por ejemplo, en lugar de manejar el dato *Mide 180cm*, maneja *Es alto con un valor de 0.8*.
* La Lógica Difusa **se construye sobre la experiencia** de los expertos: confía en la experiencia de quien ya conoce el sistema.
* La Lógica Difusa **puede mezclarse con otras técnicas clásicas** de control.
Hay muy buen material ya disponible para entrar en el mundo de la Lógica Difusa desde un punto de vista más técnico. Basta realizar una búsqueda simple para encontrar multitud de recursos gratuitos y de calidad al alcance de la mano.
(insert menu.md.html here)