**Aprendizaje Profundo (Deep Learning)** A pesar de que las redes superficiales son densas en conjuntos de funciones muy interesantes (lo que quiere decir que podremos aproximar la mayoría de los patrones que surgen en problemas naturales), eso no quiere decir que seamos capaces de encontrar una aproximación de forma sencilla, incluso teniendo un método relativamente bueno de entrenamiento como son los basados en descenso del gradiente. De hecho, es bastante común que, a medida que la complejidad del patrón crece (por ejemplo, en dimensión), el número de neuronas que tendríamos que usar en una red superficial para aproximarlo se puede disparar exponencialmente, haciendo impracticable, desde el punto de vista computacional, su uso. Para paliar este problema podemos aumentar la profundidad de la red. Esta es una de las razones por la que los últimos avances en aprendizaje automático se han logrado en gran medida gracias a las llamadas **redes neuronales profundas**. En este contexto, **profundo** se refiere a redes neuronales en las que la entrada pasa por muchas neuronas para ser procesada mientras contribuye a la salida final, una disposición no muy diferente a la del cerebro y que contrasta con las redes superficiales presentadas en la sección anterior. Una vez demostrado el potencial de estas redes, se acuñó el término **aprendizaje profundo** (**Deep Learning**) como sinónimo de *aprendizaje automático con redes neuronales profundas*. !!!side:11 Puede verse [esta entrada de la Wikipedia](https://en.wikipedia.org/w/index.php?title=Types_of_artificial_neural_networks&oldid=1053596085) para hacerse una idea de la diversidad. En realidad, las redes neuronales profundas son una clase muy amplia de modelos que contiene una gran cantidad de arquitecturas muy diversas para diferentes aplicaciones [11]. Aunque aquí solo vamos a cubrir dos arquitecturas principales, gran parte de lo que veamos será transferible a otros tipos de redes. Aunque las redes neuronales profundas pueden ser muy potentes, es difícil conseguir que funcionen correctamente y muchos aspectos de estas redes aún no se conocen bien. Vamos a comenzar esta sección explicando qué son las redes neuronales profundas, así como las técnicas y algoritmos necesarios para que funcionen, que deben ser un poco más depurados que los vistos para redes superficiales. # Redes Neuronales Profundas (Deep Neural Networks) ## Redes Feed Forward !!!side:12 La otra clase principal de redes neuronales, además de las feed forward, son las redes neuronales recurrentes, que permiten la presencia de ciclos en sus grafos. Las redes neuronales recurrentes se utilizan principalmente para el procesamiento de datos secuenciales, como el procesamiento de datos temporales, las aplicaciones del habla y de lenguaje natural. El ejemplo por excelencia de red neuronal profunda es la red neuronal **Feed Forward** (**FFN**), en la que las conexiones entre nodos no forman ciclos. Una FFN simplemente toma un conjunto de redes superficiales y las concatena, alimentando cada capa de neuronas con la salida de la capa anterior [12]. Formalicemos esta construcción: !!!def:Redes Feed Forward Sea $L \in \mathbb{N}$ y $N_0,N_1,\ldots,N_{L+1} \in \mathbb{N}$. Sean $\sigma_1,\ldots,\sigma_L$ funciones de activación, que asumiremos como funciones escalares que aplicamos puntualmente. Sean $F_i : \mathbb{R}^{N_{i-1}} \to \mathbb{R}^{N_i}$ transformaciones afines dadas por: \begin{equation*} F_i (\mathbb{x}) := A_i \mathbb{x} + \mathbb{b}_i \end{equation*} donde $A_i \in \mathbb{R}^{N_i \times N_{i-1}}$ y $\mathbb{b}_i \in \mathbb{R}^{N_i}$ para cada $i \in \{ 1, \ldots, L+1\}$. Entonces denotamos por $\mathcal{N} : \mathbb{R}^{N_0} \to \mathbb{R}^{N_{L+1}}$ a la función dada por \begin{equation} \label{eq:feedforward} \mathcal{N} := F_{L+1} \circ \sigma_L \circ F_L \circ \cdots \circ \sigma_1 \circ F_1 \end{equation} y decimos que es una **Red Neuronal Feed Forward**. Se dice que esta red tiene $L$ **capas ocultas**, $N_i$ se dice que es el **ancho** de la capa $i$ y el máximo de todos los anchos de la capa, es decir $\max_{i=1}^L \{ N_i \}$, también se llama el **ancho de la red**. Solemos etiquetar las entradas con $\mathbb{x}$, las salidas con $\mathbb{y}$ y, si es necesario, los resultados intermedios con $\mathbb{z}^{(i)} \in \mathbb{R}^{N_i}$ (también llamadas **activaciones**), que se calculan de la siguiente manera: \begin{equation*} \mathbb{z}^{(0)} := \mathbb{x} , \qquad \mathbb{z}^{(i)} := \sigma_i \left( F_i(\mathbb{z}^{(i-1)}) \right) \end{equation*} para cada $i \in \{ 1,\ldots, L+1\}$. Se pueden considerar variantes de esta arquitectura, que se siguen denominando redes feed forward, por diversos métodos. Por ejemplo, podríamos incluir funciones de activación multivariante como $\operatorname{soft-max}$ o $\operatorname{max pooling}$ (lo que nos obligaría a especificar las anchuras de entrada y salida de las capas de forma diferente, pero aún así podríamos escribir la red como en \eqref{eq:feedforward}), o podríamos considerar **conexiones de salto**, donde algunas de las salidas de una capa se pasan a capas más profundas en lugar de (o además de) la siguiente capa, como ilustra la siguiente figura:  !!!note:Anchura frente a Profundidad Anteriormente, vimos cómo una red neuronal superficial con funciones de activación ReLU da como resultado una función lineal a trozos. El primer método para modelar una función más compleja sería aumentar la anchura de la red, el número de piezas lineales escalaría linealmente con la cantidad de neuronas. Esto quiere decir que si queremos aproximar una función por medio de una lineal a trozos con $N$ trozos, necesitaremos $kN$ neuronas de anchura en la capa oculta. Por ejemplo, si quisiéramos modelar un diente de sierra con $n$ dientes con una red ReLU superficial necesitaríamos $2n$ neuronas. Pero si consideramos la red para $1$ diente: \begin{equation} \label{eq:sawtooth} f(x) := \operatorname{ReLU}(2 x) - \operatorname{ReLU}(4 x - 2) + \operatorname{ReLU}(2 x - 2) \end{equation} y la componemos con ella misma varias veces, también obtendríamos una función diente de sierra pero duplicando el número de dientes en cada iteración, dando lugar a un crecimiento exponencial en el número de composiciones. Esta es la principal ventaja de la profundidad: la complejidad de las funciones que puede modelar una red crece más rápido con la profundidad que con la anchura. Esto no quiere decir que debamos diseñar nuestras redes con la máxima profundidad y la mínima anchura. Hay que tener en cuenta ciertas compensaciones y cualquier red real debe encontrar un equilibrio entre anchura y profundidad, ya que el aumento de profundidad también incluye la aparición de algunos problemas nuevos, como veremos en la siguiente sección. ## Desvanecimiento y explosión de gradientes Como hemos comentado, no todo son ventajas con las redes profundas. Una dificultad que aparece con ellas se refiere al entrenamiento, ya que los parámetros de las capas más superficiales de la red (de las neuronas que están en las primeras capas) tienen que pasar por muchas capas antes de contribuir finalmente a la pérdida, que se calcula a partir de la salida. Para analizar cómo afecta este hecho, vamos a hacer caso omiso de las transformaciones afines de una red por el momento y centrarnos en las funciones de activación (que son las principales causantes de este hecho). !!!side:13 Teóricamente, podríamos entrenar durante más tiempo para compensar gradientes muy pequeños, pero en la práctica esto tampoco funciona debido a cómo funcionan las matemáticas de coma flotante. Concretamente, cuando trabajamos con números de coma flotante tenemos \begin{equation*} a + b = a \quad \text{if} \quad |b| \ll |a|, \end{equation*} por lo que una actualización lo suficientemente pequeña de un parámetro no cambia realmente el parámetro. !!!note:Saturación, desvanecimiento y explosión de la sigmoide Sea $\sigma$ la función de activación sigmoidea dada por $\sigma(x):=\frac{1}{1+e^{-x}}$, y denotamos: \begin{equation*} \sigma^L := \underbrace{\sigma \circ \sigma \circ \cdots \circ \sigma}_{L} \end{equation*} Para calcular la derivada de $\sigma^L$ aplicamos la regla de la cadena, que nos devuelve una relación por recursión: \begin{equation*} \frac{\partial \sigma^L}{\partial x} (a) = \sigma' \left( \sigma^{L-1}(a) \right) \, \frac{\partial \sigma^{L-1}}{\partial x} (a) \end{equation*}  La figura adyacente muestra las gráficas de la función de activación sigmoidea y su derivada. Obsérvese que la derivada es como máximo $\frac{1}{4}$ y tiende a cero rápidamente a medida que $x \to \pm\infty$, esto se llama **saturación**. Por tanto: \begin{equation*} \left| \frac{\partial}{\partial x} \sigma^L(a) \right| \leq \left( \frac{1}{4} \right)^L \end{equation*} En consecuencia, realizar un paso de descenso de gradiente de la forma \begin{equation*} a_{i+1} = a_i - \eta \, \frac{\partial}{\partial x} \sigma^L (a_i) \end{equation*} no cambiaría mucho el valor del parámetro, un problema que empeora con cada capa adicional. Peor es que $\sigma'(x)$ llega a cero rápidamente para valores absolutos grandes de $x$, como puede verse en la figura. En este régimen, cuando $\sigma(x)$ se aproxima a $0$ o $1$, decimos que la sigmoidea está **saturada**. Este comportamiento de los gradientes cada vez más pequeños cuanto más profunda es la red se denomina **problema de desvanecimiento del gradiente** [13].  Con otras funciones de activación también puede producirse el fenómeno opuesto, en el que los gradientes se hacen cada vez más grandes, lo que conduce a un entrenamiento inestable denominado **explosión de gradiente**.  Podemos contrastar el comportamiento de la sigmoide con la ReLU en la misma situación: !!!note:Comportamiento de ReLU Recordemos que la ReLU se define como $\operatorname{ReLU}(x):=\max\{0,x\}$, entonces definimos: \begin{equation*} \operatorname{ReLU}^L := \underbrace{\operatorname{ReLU} \circ \operatorname{ReLU} \circ \cdots \circ \operatorname{ReLU}}_{L} \end{equation*} Calculando la derivada obtenemos: \begin{equation} \label{eq:relun_deriv} \frac{\partial}{\partial a} \operatorname{ReLU}^L (a) = \begin{cases} \ 1 \quad &\text{si } a > 0, \\ \ 0 &\text{en otro caso} \end{cases} \end{equation} que no depende del número de capas, $L$. Conceptualmente, \eqref{eq:relun_deriv} puede interpretarse como una ReLU que proporciona una derivada $1$ para los parámetros que están afectando realmente a la pérdida (independientemente de la capa en la que reside el parámetro) y una derivada 0 para los parámetros que no lo hacen. El hecho de que las ReLU eludan (al menos parcialmente) el problema del desvanecimiento/explosión del gradiente explica su popularidad en las redes neuronales profundas. Esto no quiere decir que las ReLU no tengan problemas: si una entrada a una ReLU es negativa tendrá un gradiente nulo, decimos que la ReLU o la neurona está **muerta**. En consecuencia, todas las neuronas en la capa anterior que sólo (o predominantemente) se alimentan de esa neurona también tendrán un gradiente nulo (o cerca de 0). El conjunto de neuronas bajo su influencia se conocen como su **sombra** (en morado en la figura). Durante el entrenamiento, qué neuronas están muertas y dónde se proyecta la sombra cambia de un lote a otro. Mientras la mayoría de las neuronas no estén permanentemente en la sombra, deberíamos ser capaces de entrenar correctamente la red. Sin embargo, si por casualidad partimos de una inicialización desafortunada es muy posible que una gran parte de nuestra red esté permanentemente atascada con gradientes nulos, este fenómeno se llama el problema del **ReLU en extinción**. Por supuesto, la elección de la función de activación no es lo único que tenemos que considerar. Los gradientes en una red real también dependen de los valores actuales de los parámetros de las transformadas afines. Así que conviene inicializar esos parámetros a valores que no causen problemas de desvanecimiento o explosión de gradiente desde el principio. Veremos algo sobre inicialización de los parámetros más adelante. ## Escalado a datos de alta dimensión Si consideramos que todos los componentes de una de las matrices $A_i$ de \eqref{eq:feedforward} son parámetros entrenables, entonces decimos que la capa $i$ está **completamente conectada** o es **densa**, lo que significa que todas las salidas de la capa dependen de todas las entradas. Cuando todas las capas están totalmente conectadas decimos que la red está **completamente conectada**. Por supuesto, no es necesario tener todos los componentes de las matrices $A_i$ y los vectores $\mathbb{b}_i$ como parámetros entrenables. De hecho, la FFN completamente conectada de \eqref{eq:feedforward} no se utiliza a menudo en la práctica, pero muchas arquitecturas son especializaciones de este tipo adaptadas a aplicaciones específicas. La especialización en este contexto significa principalmente elegir qué componentes de los $A_i$'s y $\mathbb{b}_i$'s son entrenables y cuáles están fijados a alguna constante elegida. La razón principal por la que no se utilizan redes totalmente conectadas es que simplemente no se adaptan a datos de alta dimensión: !!!side:14 Almacenar esa cantidad de números en formato de coma flotante de 32 bits ocuparía la friolera de 36 terabytes, y eso que se trata de una sola matriz. !!!ejemplo Consideremos una aplicación en la que queremos aplicar una transformación en una imagen en color de $1000 \times 1000$. La entrada y la salida serían elementos del espacio $\mathbb{R}^{3 \times 1000 \times 1000}$, una transformación lineal en ese espacio vendría dada por una matriz: \begin{equation*} A \in \left( \mathbb{R}^{3 \times 1000 \times 1000} \right)^2 \end{equation*} es decir, con $9 \cdot 10^{12}$ componentes [14]. Está claro que esto descarta las redes totalmente conectadas para aplicaciones de alta dimensión como son las imágenes. Se emplean 3 estrategias para hacer frente a este problema: * **Matrices dispersas** (**sparsity**): donde se fijan a 0 la mayoría de sus entradas, por lo que, usando estructuras de datos adecuadas, no necesitamos almacenar esas entradas y simplificamos el cálculo que tenemos que realizar puesto que ya conocemos el resultado de las partes reducidas a 0. * **Pesos distribuidos**: se reutiliza el mismo parámetro en varias ubicaciones de la matriz. En este caso sólo tenemos que almacenar los parámetros únicos y no toda la matriz. Compartir pesos es técnicamente un caso especial de la última estrategia. * **Parametrización**: dejamos que los componentes de la matriz dependan de un número (pequeño) de parámetros. En este caso, almacenamos los parámetros y calculamos los componentes de la matriz cuando es necesario. !!!ejemplo Las siguientes matrices son un ejemplo de comparación entre el caso totalmente conectado y las tres estrategias propuestas: \begin{equation*} \underset{ \strut \textsf{(totalmente conectada)} } { \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} } , \qquad \underset{ \strut \textsf{(dispersa)} } { \begin{bmatrix} a & & \\ & & \\ & b & \hphantom{b} \end{bmatrix} } , \qquad \underset{ \strut \textsf{(distribución de pesos)} } { \begin{bmatrix} a & b & b \\ b & a & b \\ b & b & a \end{bmatrix} } , \qquad \underset{ \strut \textsf{(parametrizado)} } { \begin{bmatrix} f_{1}(a,b) & f_{2}(a,b) & f_{3}(a,b) \\ f_{4}(a,b) & f_{5}(a,b) & f_{6}(a,b) \\ f_{7}(a,b) & f_{8}(a,b) & f_{9}(a,b) \end{bmatrix} } , \end{equation*} necesitamos almacenar 9 números para la matriz totalmente conectada pero sólo 2 números para cada una de las otras matrices. Estas 3 estrategias no se excluyen mutuamente y más adelante veremos una arquitectura que utiliza una combinación de dispersión con distribución de pesos. # Inicialización Como ocurre siempre con los métodos de optimización por aproximaciones sucesivas, en el caso de las redes profundas, los valores iniciales de los parámetros pueden llegar a marcar una diferencia significativa en el funcionamiento de los algoritmos basados en SGD. Pero, además, unos parámetros iniciales demasiado extremos (pequeños/grandes en magnitud) pueden provocar problemas de desvanecimiento/explosión del gradiente y causar problemas inmediatos para el entrenamiento. !!!side:15 Es posible que para una aplicación concreta se pueda desarrollar un esquema determinista que ofrezca un punto de partida mucho mejor para el entrenamiento que el producido por esquemas estocásticos, pero los métodos estocásticos aseguran un comportamiento suficientemente bueno sin necesidad de usar un conocimiento profundo del dominio del problema. !!!side:16 Por ejemplo, GPT-3 utiliza 175.000 millones de parámetros y su entrenamiento ha costado, según se informa, 4 millones de US$. Por tanto, mejorar los esquemas de inicialización puede tener un valor económico considerable. Para evitar este problema, vamos a ver algunos esquemas de inicialización estocástica que proporcionan un punto de partida práctico para el entrenamiento de una red [15]. Un buen esquema de inicialización permite a la red alcanzar un mayor nivel de rendimiento en menos tiempo. Esto puede tener importantes consecuencias para las grandes redes de producción [16]. Generalmente, utilizamos métodos estocásticos para la inicialización ya que es necesario que los valores iniciales de los parámetros en una capa sean suficientemente diferentes entre sí (si los valores fueran similares, sus gradientes también lo serían, bloqueando la red en un estado de poco cambio y capacidad de aprendizaje). El método más sencillo para conseguir esta diversidad consiste en extraer los valores de una distribución de probabilidad. Por lo general, las distribuciones que se utilizan son, o bien la normal $\mathcal{N}(0,\sigma^2)$, o la uniforme $\operatorname{Unif}[-a,a]$, donde tenemos que elegir $\sigma^2$ o $a$ para evitar los problemas señalados. A cada grupo de parámetros (los coeficientes lineales y los sesgos de cada capa) se les suele asignar su propia distribución. Veremos algunos métodos que se aplican en casos reales para elegir estas distribuciones. En lo que sigue se harán muchas suposiciones (algunas incluso verificablemente incorrectas en las redes que se suelen emplear) para llegar a fórmulas sencillas. A pesar de la forma tosca y poco elegante en que se van a derivar estos esquemas de inicialización, son ampliamente utilizados por la sencilla razón de que funcionan. No resuelven totalmente el problema de desvanecimiento/explosión del gradiente, pero mejoran significativamente el rendimiento de los algoritmos de descenso de gradiente. ## Control de la Varianza Para desarrollar una distribución de probabilidad adecuada con la que inicializar los parámetros, empezamos considerando la entrada a una neurona como una variable aleatoria $X \in \mathbb{R}^n$ con valor vectorial. La salida de una neurona es entonces una variable aleatoria $Y \in \mathbb{R}^m$: \begin{equation*} Y = \sigma \left( A X +\mathbb{b} \right) \end{equation*} para alguna matriz constante $A \in \mathbb{R}^{m \times n}$, vector de sesgo $\mathbb{b} \in \mathbb{R}^m$ y función de activación $\sigma$. O, alternativamente, escrito por componentes: \begin{equation} \label{eq:Y_i} Y_i = \sigma \left( \sum_{j=1}^n A_{ij} X_j + b_i \right) \end{equation} La idea es inicializar $A$ y $\mathbb{b}$ para que la varianza de la señal no cambie demasiado de capa a capa, es decir: \begin{equation*} \sum_{i=1}^m Var(Y_i)^2 \approx \sum_{j=1}^n Var(X_j)^2 \end{equation*} Controlar la norma $L^2$ de las varianzas de las señales no es necesariamente la única posibilidad en este caso, pero es la opción con la que procederemos. Calcular varianzas de funciones de variables aleatorias es difícil en general. Los esquemas que vamos a estudiar dependen de la siguiente aproximación. !!!teorema:Lema Sea $X$ una variable aleatoria de valor real y sea $f:\mathbb{R}\to\mathbb{R}$ una función diferenciable. Entonces \begin{equation*} Var\left( f(X) \right) \approx f' \left( \mathbb{E}[X] \right)^2 \cdot Var(X), \end{equation*} suponiendo que la varianza de $X$ es finita y $f'$ es diferenciable. !!!demo:Demostración Sea $m := \mathbb{E}[X]$ y aproximemos $f$ por su linealización alrededor de $m$: $f(X) \approx f(m) + f'(m) (X - m)$. Entonces podemos encontrar: $$\begin{align*} Var\left( f(X) \right) &= \mathbb{E}\left[ \left( f(X) - \mathbb{E}[f(X)] \right)^2 \right] \\ &\approx \mathbb{E}\left[ \left( f(m) + f'(m) (X - m) - \mathbb{E}[f(m) + f'(m) (X - m)] \right)^2 \right] \\ &= \mathbb{E}\left[ \left( f(m) + f'(m) (X - m) - f(m) - f'(m) \,\mathbb{E}[(X - m)] \right)^2 \right] \\ &= \mathbb{E}\left[ \left( f'(m) (X - m) \right)^2 \right] \\ &= f'(m)^2 \, \mathbb{E}\left[ (X-m)^2 \right] \\ &= f' \left( \mathbb{E}[X] \right)^2 \cdot Var(X). \end{align*}$$ Intuitivamente, este lema se puede interpretar como: si la varianza de $X$ es pequeña y $f'$ está razonablemente acotada entonces la varianza de $f(X)$ también será pequeña. Aplicando este lema a \eqref{eq:Y_i} nos lleva a: \begin{equation*} Var(Y_i) \approx \sigma' \left( \sum_{j=1}^n A_{i j} \, \mathbb{E}[X_j] + b_i \right)^2 \ \left( \sum_{j=1}^n A_{i j}^2 \ Var(X_j) \right) \end{equation*} Si $\mathbb{E}[X_1]=\ldots=\mathbb{E}[X_n]$ y $Var(X_1)=\ldots=Var(X_n)$, entonces: \begin{equation*} Var(Y_i) \approx \underbrace{ \sigma' \left( \mathbb{E}[X_1] \sum_{j=1}^n A_{i j} + b_i \right)^2 \ \left( \sum_{j=1}^n A_{i j}^2 \right)}_{\text{idealmente}\ \approx 1} \ Var(X_1) \end{equation*} Cuando el término remarcado es aproximadamente 1, las varianzas de las salidas $Y_i$ son aproximadamente iguales a las de las entradas $X_j$. Para conseguir este efecto, supongamos que $A_{i j}$ y $b_i$ son variables aleatorias: $A_{i j} \sim \mu_1$ y $b_i \sim \mu_2$ para todo $i$ y $j$ en sus respectivos rangos y donde $\mu_1$ y $\mu_2$ son alguna elección de distribuciones de probabilidad escalares. Lo ideal sería elegir $\mu_1$ y $\mu_2$ de modo que: \begin{equation} \label{eq:E=1} \mathbb{E}\left[ \sigma' \left( \mathbb{E}[X_1] \sum_{j=1}^n A_{i j} + b_i \right)^2 \ \left( \sum_{j=1}^n A_{i j}^2 \right) \right] = 1 \end{equation} lo que impone una condición en la elección de distribuciones de probabilidad que asegura que las varianzas de las señales entre capas permanecen bajo control (al menos al inicio del entrenamiento). Veamos un par de ejemplos que muestran cómo se utiliza \eqref{eq:E=1}: !!!side:17 Esta condición adicional es bastante habitual tras un proceso de preprocesado en el dataset de entrenamiento. !!!ejemplo:Sigmoide con entradas equilibradas Bajo las condiciones anteriores, supongamos que $\sigma$ es la función de activación sigmoidea y tenemos $\mathbb{E}[X_i]=0$, es decir, tenemos entradas equilibradas [17]. Además queremos una inicialización de parámetros equilibrada, es decir, $\mathbb{E}[b_i]=0$ y $\mathbb{E}[A_{i j}]=0$ para todo $i,j$ en sus respectivos rangos. Como $\mathbb{E}[X_i]=0$, \eqref{eq:E=1} se reduce a: \begin{equation*} \mathbb{E}\left[ \sigma' \left( b_i \right)^2 \ \left( \sum_{j=1}^n A_{i j}^2 \right) \right] = \mathbb{E}\left[ \sigma' \left( b_i \right)^2 \right] \, \mathbb{E}\left[ \sum_{j=1}^n A_{i j}^2 \right] \end{equation*} ya que los $b_i$'s y $A_{i j}$'s son independientes. Sabemos que $0 < \sigma'(x) \leq \frac{1}{4}$ y que el máximo se alcanza en $x=0$. Por lo tanto, para que ese primer factor no sea demasiado pequeño, necesitamos que la varianza de $b_i$ sea pequeña, puesto que ya hemos decidido fijar $\mathbb{E}[b_i]=0$. Por supuesto, la varianza más pequeña posible es cero, así que seamos inflexibles y fijemos $b_i=0$ para todo $i$. Así, la expresión anterior se convierte en \begin{equation*} \sigma'(0)^2 \ n \, \mathbb{E} \left[ A_{i j}^2 \right] = \frac{n}{16} \, \mathbb{E} \left[ (A_{i j} - 0)^2 \right] = \frac{n}{16} \, \mathbb{E} \left[ (A_{i j} - \mathbb{E}[A_{i j}])^2 \right] = \frac{n}{16} \, Var(A_{i j}) \end{equation*} que es igual a 1 si \begin{equation*} Var(A_{i j}) = \frac{16}{n} \end{equation*} Así que podríamos elegir nuestra distribución de probabilidad para los coeficientes lineales como la distribución normal $\mathcal{N}(0,\frac{16}{n})$ o la distribución uniforme $\operatorname{Unif}\left[ -\frac{4\sqrt{3}}{n}, \frac{4\sqrt{3}}{n}\right]$. Por supuesto, la elección del tipo de distribución es libre siempre que el valor esperado sea cero y la varianza sea $\frac{16}{n}$, pero en la práctica normalmente sólo nos encontraremos con distribuciones normales o uniformes. En cualquier caso, esta elección de valores esperados y varianzas proporcionará cierta garantía de que las señales no explotarán ni se desvanecerán a medida que viajan a través de la red (al menos, al comienzo del entrenamiento). !!!ejemplo:ReLU con entradas equilibradas Bajo las condiciones anteriores, supongamos ahora que $\sigma$ es la función de activación ReLU y vamos a inicializar tanto nuestros coeficientes lineales como los sesgos con una distribución uniforme $\operatorname{Unif}[-a,a]$, nuestro objetivo es elegir $a>0$ de forma adecuada. Supongamos de nuevo que las entradas están equilibradas, es decir, $\mathbb{E}[X_i]=0$, entonces la expresión de \eqref{eq:E=1} queda como: $$\begin{align*} \mathbb{E} \left[ \operatorname{ReLU}'\left( b_i\right)^2 \ \left( \sum_{j=1}^n A_{i j}^2 \right) \right] &= \mathbb{E} \left[ \mathbb{1}_{b_i>0} \right] \ \mathbb{E}\left[ \left( \sum_{j=1}^n A_{i j}^2 \right) \right] \\ &= \mathbb{P} \left( b_i > 0 \right) \ n \, Var(A_{i j}) \\ &= \frac{n}{2} \, Var(A_{i j}) \\ &= \frac{n a^2}{6}, \end{align*}$$ que es igual a 1 si $a=\sqrt{\frac{6}{n}}$ por lo que deberíamos generar $A_{i j}$'s y $b_i$'s por medio de la distribución $\operatorname{Unif}\left[ - \sqrt{\frac{6}{n}}, \sqrt{\frac{6}{n}} \right]$. ## Inicialización Xavier !!!side:18 El nombre del primer autor es Xavier Glorot y por esa razón el esquema que vamos a ver se conoce comúnmente como **Inicialización Glorot o Xavier**. Los esquemas de inicialización de la sección anterior se han centrado en el control de la varianza de las señales que avanzan a través de la red. Aunque esto ayuda a controlar el problema del gradiente que se desvanece/explosiona, también podemos observar los gradientes directamente a medida que se propagan a través de la red, este es el enfoque adoptado por Glorot y Bengio en [#glorot2010] [18]. La idea es tratar las derivadas parciales de la función de pérdida con respecto a los coeficientes lineales y los sesgos también como variables aleatorias. Consideremos una situación con una función de activación lineal y sin sesgo: \begin{equation*} Y_i = \sum_{j=1}^n A_{i j} X_j, \end{equation*} donde suponemos que todas las entradas $X_j$ se distribuyen i.i.d. con $\mathbb{E} \left[X_i \right]=0$. Además, queremos inicializar nuestros coeficientes $A_{i j}$ con media cero también. Como los $A_{i j}$ y $X_j$ son independientes, la varianza se distribuye sobre la suma. Además tenemos que: \begin{equation*} Var(A_{i j} X_j) = \mathbb{E}[X_j]^2 Var(A_{i j}) + \mathbb{E}[A_{i j}]^2 Var(X_j) + Var(A_{i j}) Var(X_j) = Var(A_{i j}) Var(X_j) \end{equation*} ya que $\mathbb{E}[X_j]=\mathbb{E}[A_{i j}]=0$. De donde: \begin{equation*} Var(Y_i) = \sum_{j=1}^n Var(A_{i j}) Var(X_j) = n Var(A_{i j}) Var(X_j) \end{equation*} Por tanto, para la propagación de la señal hacia adelante tenemos $Var(Y_i)=Var(X_j)$ si \begin{equation} \label{eq:var_forward} Var(A_{i j})=\frac{1}{n} \end{equation} Pero también podemos observar la propagación del gradiente hacia atrás. Sea $\ell$ una función de pérdida al final de la red, entonces podemos ver las derivadas parciales de $\ell$ con respecto a las entradas y salidas como variables aleatorias también. Llamemos a estas variables aleatorias $\frac{\partial \ell}{\partial X_i}$ y $\frac{\partial \ell}{\partial Y_i}$, aplicando la regla de la cadena nos da \begin{equation*} \frac{\partial \ell}{\partial X_j} = \sum_{i=1}^m \frac{\partial \ell}{\partial Y_i} \frac{\partial Y_i}{\partial X_j} = \sum_{i=1}^m \frac{\partial \ell}{\partial Y_i} A_{i j} \end{equation*} Ahora hacemos la misma suposición acerca de los gradientes hacia atrás como lo hicimos acerca de las señales hacia adelante, es decir, que las derivadas parciales $\frac{\partial \ell}{\partial Y_i}$ son i.i.d. con media cero. Entonces podemos hacer el mismo cálculo que antes y encontrar \begin{equation*} Var\left( \frac{\partial \ell}{\partial X_j} \right) = m Var\left( A_{i j} \right) Var \left( \frac{\partial \ell}{\partial Y_i} \right) \end{equation*} Por lo tanto si queremos tener $Var\left( \frac{\partial \ell}{\partial X_j} \right)=Var \left( \frac{\partial \ell}{\partial Y_i} \right)$ para la propagación del gradiente hacia atrás tenemos que establecer \begin{equation} \label{eq:var_backward} Var(A_{i j}) = \frac{1}{m} \end{equation} Ahora, a menos que $n=m$ no podemos satisfacer \eqref{eq:var_forward} y \eqref{eq:var_backward} al mismo tiempo, pero podemos llegar a un acuerdo y establecer \begin{equation} \label{eq:var_forward_backward} Var(A_{i j}) = \frac{2}{n+m} \end{equation} Bajo esta elección podemos utilizar la distribución normal $\mathcal{N}(0,\frac{2}{n+m})$ o la distribución uniforme $\operatorname{Unif}\left[ -\sqrt{\frac{6}{n+m}}, \sqrt{\frac{6}{n+m}} \right]$ para extraer nuestros coeficientes $A_{i j}$. Por supuesto, en la realidad nunca utilizamos la función de activación lineal. El esquema original de inicialización de Xavier se ha ampliado para incluir funciones de activación específicas. Por ejemplo para el ReLU de [#he2015], llegan a \begin{equation*} Var(A_{i j}) = \frac{4}{n+m} \end{equation*} !!!side:19 Otras opciones de función de activación conducen a la introducción de otros multiplicadores en la misma fórmula básica \eqref{eq:var_forward_backward}: \begin{equation*} Var(A_{i j}) = \alpha^2 \frac{2}{n+m}, \end{equation*} donde $\alpha$ se denomina **ganancia** y depende de la elección de la función de activación. Lo que intuitivamente tiene sentido: como ReLU es cero en la mitad de su dominio, es necesario aumentar la varianza de los coeficientes para mantener constantes las varianzas de las señales/gradientes [19]. # Redes Neuronales Convolucionales Anteriormente vimos que el uso de redes totalmente conectadas para datos de alta dimensión, como las imágenes, no es una opción viable debido a los requisitos de memoria y computación que conlleva. La solución propuesta ha consistido en reducir la cantidad efectiva de parámetros mediante una combinación de matrices dispersas y reparto/parametrización de pesos. La forma exacta de dispersar la red y los pesos que debían compartirse o parametrizarse debía determinarse aplicación por aplicación. !!!side:20 Por ejemplo, señales temporales (1D), imágenes (2D) o datos volumétricos (3D). !!!side:21 Por ejemplo, no procesamos la parte izquierda de una imagen de forma distinta a la parte derecha. En esta sección mostraremos una combinación de uso de matrices dispersas y reparto de pesos que se adapta muy bien a los datos que tienen una estructura espacial intrínseca [20]. Lo que tienen en común estos tipos de datos espaciales es la homogeneidad, que permite tratar cada *parte* de los datos de entrada de la misma forma [21]. El tipo de red que explota esta estructura espacial se denomina **red neuronal convolucional** (CNN, por sus siglas en inglés) que, como su nombre indica, emplean la operación de convolución, así como la operación de agrupación estrechamente relacionada. Veremos cómo se definen la convolución discreta y el pooling y cómo se utilizan para construir una CNN profunda. ## Convolución discreta !!!def:Convolución Continua Recordemos que en el entorno continuo la convolución de dos funciones $k,f : \mathbb{R} \to \mathbb{R}$ se define como: \begin{equation} \label{eq:classic_convolution} (k * f)(x) := \int_{\mathbb{R}} k(x-y) \, f(y) \, \d y \end{equation} que puede interpretarse como un filtro (**kernel** o **núcleo**), $k$, que se traslada sobre los datos, $f$, y en cada posición trasladada se toma el producto interno de $L^2$. !!!def:Correlación cruzada discreta y convolución en 1D Sea $f \in \mathbb{R}^n$ (la entrada) y $k \in \mathbb{R}^m$ (el kernel), entonces la **correlación cruzada discreta** $(k \star f) \in \mathbb{R}^{n-m+1}$ viene dada por: \begin{equation*} (k \star f)_i := \sum_{j=1}^{m} k_j \, f_{i+j} \end{equation*} para $i \in \{ 1, \ldots, n-m+1 \}$. La **convolución discreta** se define de forma similar pero con una de las entradas invertida (recorrida del final hacia el principio): \begin{equation*} (k * f)_i := \sum_{j=1}^{m} k_{m-j} \, f_{i+j} \end{equation*} para $i \in \{ 1, \ldots, n-m+1 \}$. !!!note Haciendo una sustitución de índice ($j'=i+j$) en la definición de convolución discreta (y volviendo a notar $j'=j$) se hace más evidente la relación con la convolución continua \eqref{eq:classic_convolution}: \begin{equation*} (k * f)_i = \sum_{j=i+1}^{i+m} k_{i-j + m} \, f_j \end{equation*} !!!side:22 La mayoría de los operadores de *convolución* en el software de aprendizaje profundo se implementan, de hecho, como correlaciones cruzadas. Adoptaremos la misma convención y hablaremos de temas como capas de convolución y redes neuronales convolucionales, pero la operación subyacente real que utilizaremos es la correlación cruzada. La idea aquí es dejar que las componentes del kernel $k \in \mathbb{R}^m$ sean parámetros entrenables. En ese contexto, no importa si el kernel se invierte o no y no hay ninguna razón real para distinguir la convolución de la correlación cruzada (simplemente, se aprenden los parámetros en una dirección o en otra). Por ello, en el campo del aprendizaje profundo es habitual referirse a ambas operaciones como convolución [22]. Al igual que en el caso continuo, la convolución discreta puede generalizarse a dimensiones superiores, aunque aquí sólo estudiaremos el caso discreto bidimensional, ya que la extensión a dimensiones superiores es sencilla. Para simplificar un poco las expresiones resultantes, nos limitaremos a kernels cuadrados ($k \in \mathbb{R}^{m \times m}$), que es el caso más usado. !!!side:23 El operador de convolución, $*$, puede extenderse a 2 dimensiones de forma similar, pero sólo utilizaremos la correlación cruzada para el resto de nuestra discusión sobre redes neuronales convolucionales. 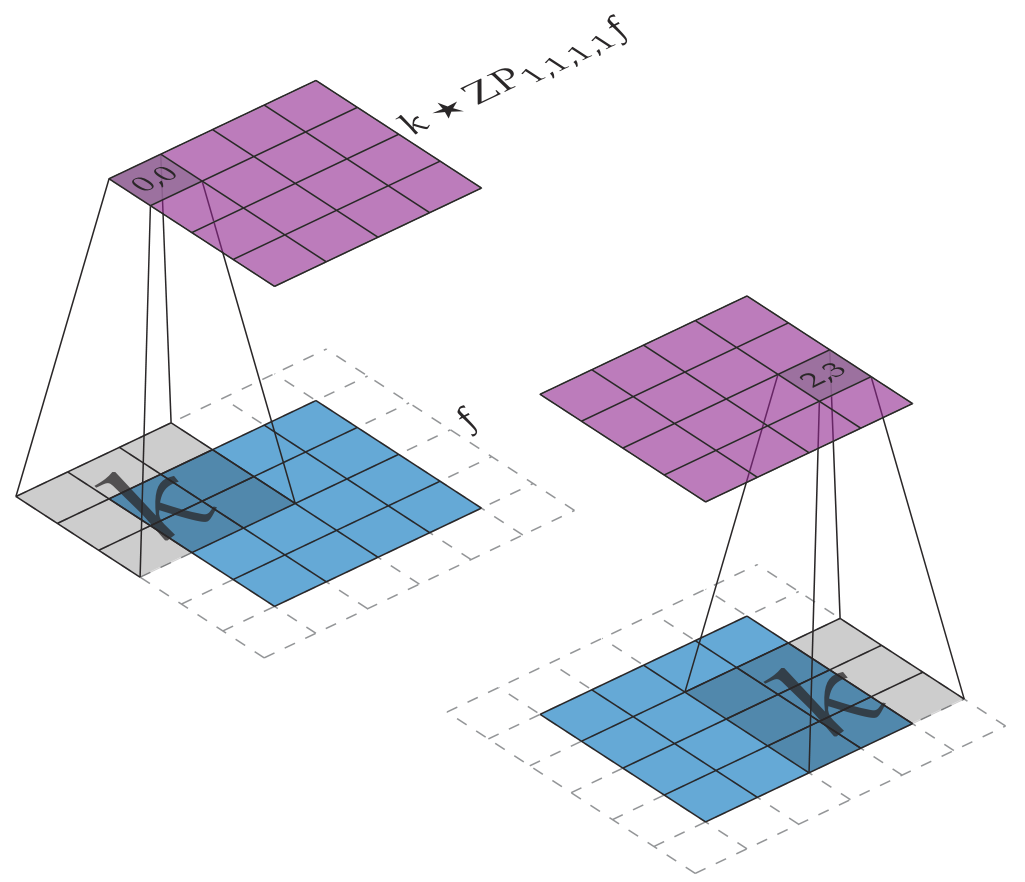!!!side:24 Ilustración de la convolución (o correlación cruzada) en 2D: La entrada $f \in \mathbb{R}^{4 \times 4}$ (color azul) se convoluciona con el núcleo $k \in \mathbb{R}^{3 \times 3}$, que produce una salida $(k \star f) \in \mathbb{R}^{2 \times 2}$ (color púrpura).  !!!def:Correlación cruzada discreta en 2D Sea $f \in \mathbb{R}^{h \times w}$ (la entrada) y $k \in \mathbb{R}^{m \times m}$ (el kernel), entonces su **correlación cruzada discreta**, $(k \star f) \in \mathbb{R}^{(h-m+1) \times (w-m+1)}$, viene dada por: \begin{equation*} (k \star f)_{i_1 i_2} := \sum_{j_1,j_2=1}^{m} k_{j_1,j_2} \, f_{i_1 + j_1, i_2 + j_2} \end{equation*} para $i_1 \in \{ 1,\ldots, h-m+1 \}$ y $i_2 \in \{ 1, \ldots, w-m+1 \}$ [23, 24]. Llamamos a $h$ la *altura* y a $w$ la segunda la *anchura* de $f$. ## Padding En la operación de convolución anterior la salida es de menor tamaño que la entrada. Dependiendo de nuestro objetivo, esto puede ser deseable o no. Si reducir el tamaño de la salida no es deseable, podemos utilizar relleno (*Padding*, por su término en inglés) para asegurarnos de que el tamaño de la salida es el mismo que el de la entrada. El tipo más común de *padding* es el *padding cero*, que veremos para el caso bidimensional: !!!def:Padding cero en 2D Sea $f \in \mathbb{R}^{h \times w}$ y $p_t,p_b,p_l,p_r\in \mathbb{N}$ (que leemos como los *padding* superior, inferior, izquierdo y derecho, respectivamente). Entonces definimos $\operatorname{ZP}_{p_t,p_b,p_l,p_r} f \in \mathbb{R}^{(h+p_t+p_b)\times(w+p_l+p_r)}$ como: \begin{equation*} \operatorname{ZP}_{p_t,p_b,p_l,p_r} f_{i_1,i_2} := \begin{cases} 0 \qquad & \text{si } i_1 < p_t \text{ o } i_1 \geq h + p_t \\ & \text{ o } i_2 < p_l \text{ o } i_2 \geq w + p_l, \\ f_{i_1-p_t,\,i_2-p_l} & \text{en caso contrario,} \end{cases} \end{equation*} para cada $i_1 \in \{ 1,\ldots,h+p_t+p_b \}$ y $i_2 \in \{1,\ldots,w+p_l+p_r \}$. !!!side  !!!teorema Si $f \in \mathbb{R}^{h \times w}$, $k\in \mathbb{R}^{m \times m}$ y: \begin{equation*} p_t := \left\lfloor \frac{m-1}{2} \right\rfloor ,\quad p_b := \left\lceil \frac{m-1}{2} \right\rceil ,\quad p_l := \left\lfloor \frac{m-1}{2} \right\rfloor ,\quad p_r := \left\lceil \frac{m-1}{2} \right\rceil , \end{equation*} entonces $k \star \operatorname{ZP}_{p_t,p_b,p_l,p_r} f \in \mathbb{R}^{h \times w}$. Existen muchas más técnicas de padding, sólo varían en cómo se eligen los valores fuera de los límites. ## Max Pooling La segunda operación habitual en las CNN es $\operatorname{max pooling}$ (agrupación de máximos). Ya vimos anteriormente una función de activación llamada $\operatorname{max pooling}$, que es exactamente la que se utiliza en una CNN pero con una elección particular de subconjuntos sobre los que tomar los máximos que funciona bien con la estructura espacial de los datos. La idea es hacer que una *ventana* se deslice sobre los datos de entrada tal y como lo hace un kernel de convolución y, a continuación, tomar el valor máximo en cada ventana. Vamos a echar un vistazo a un tipo particular de $\operatorname{max pooling}$ 2D que se encuentra comúnmente en las CNN utilizadas para el procesamiento de imágenes y aplicaciones de clasificación. 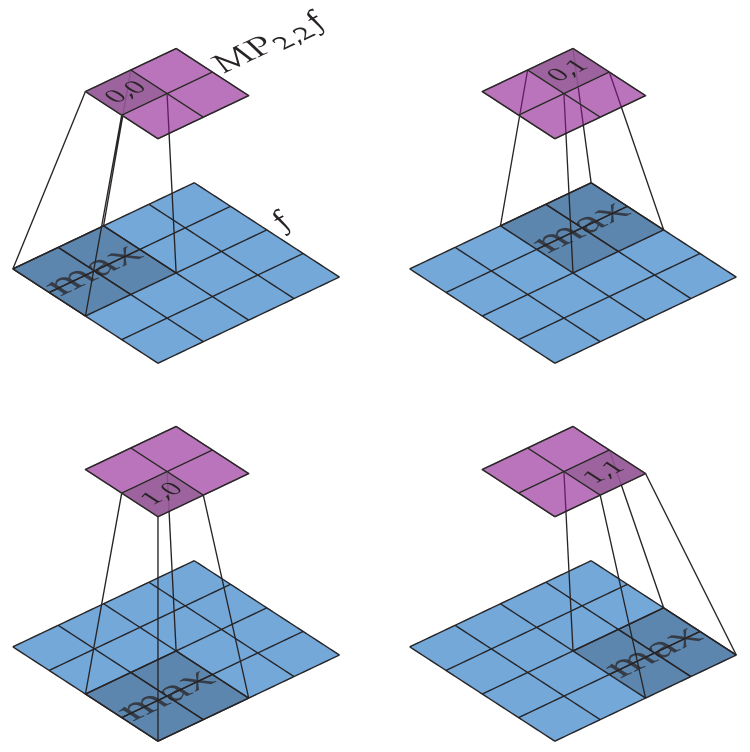!!!side $\operatorname{max pooling}$ actúa de forma similar a la convolución, donde una ventana de cierto tamaño se desliza sobre la entrada, pero en lugar de tomar una suma ponderada dentro de la ventana tomamos el valor máximo. Normalmente, la ventana se desplaza en pasos iguales a su tamaño, de modo que las salidas son los máximos de conjuntos disjuntos de la entrada. La operación de agrupación de la figura se suele denominar $\operatorname{max pooling} 2\times 2$, en referencia tanto al tamaño de la ventana como al intervalo utilizado.  !!!def:$m \times m$ $\operatorname{max pooling}$ en 2D Sea $f \in \mathbb{R}^{h \times w}$ y $m \in \mathbb{N}$. Entonces definimos $\operatorname{MP}_{m,m} f \in \mathbb{R}^{\lfloor\frac{h}{m}\rfloor \times \lfloor\frac{w}{m}\rfloor}$ como \begin{equation*} \operatorname{MP}_{m,m} f_{i_1,i_2} := \max_{\substack{ 1 \leq j_1 \leq m \\ 1 \leq j_2 \leq m }} f_{(i_1-1) m + j_1, (i_2-1) m + j_2} \end{equation*} para cada $i_1 \in \{ 1 ,\ldots, \lfloor\frac{h}{m}\rfloor \}$ y $i_2 \in \{ 1 ,\ldots, \lfloor\frac{w}{m}\rfloor \}$. Hay que tener en cuenta dos cosas sobre esta definición en particular: 1. En primer lugar, si $h$ y/o $w$ no es divisible por $m$ entonces algunos valores en los bordes serán ignorados por completo y no contribuirán a la salida. Podríamos modificar la definición para resolver esto, pero en la práctica $m$ se suele fijar en $2$ y así en el peor de los casos perdemos una sola fila de valores en el borde (sólo si la entrada tiene dimensiones impares). 2. En segundo lugar, movemos la ventana en pasos de $m$ en ambas direcciones en lugar de dar pasos de $1$, esto se llama tener un **stride** (paso) de $m$. Tener un stride mayor que $1$ permite que el $\operatorname{max pooling}$ reduzca rápidamente las dimensiones de los datos. La figura siguiente muestra un ejemplo de cómo funciona $\operatorname{MP}_{2,2}$. ## Capas Convolucionales Podemos ver ya cómo se utilizan las convoluciones/correlaciones cruzadas en una red neuronal. Notemos que hay ciertas diferencias con respecto a como se han presentado en secciones anteriores: En primer lugar, organizamos nuestras entradas y salidas de forma diferente, en lugar de que las entradas y salidas sean elementos de $\mathbb{R}^n$, queremos mantener la estructura espacial. En el caso 2D recibiremos elementos de $\mathbb{R}^{h \times w}$ para alguna elección de $h,w \in \mathbb{N}$, que llamaremos **mapas 2D** o simplemente **maps**. Además, haremos uso de mapas que usan múltiples **canales**, lo que sería equivalente a trabajar simultáneamente con varios mapas (reflejando distinta información superpuesta de un mismo objeto, por ejemplo). Concretamente, supongamos que tenemos una red profunda donde indexamos el número de capas con $i$, entonces denotamos la entrada de la capa $i$ como un elemento de $\mathbb{R}^{C_{i-1} \times h_{i-1} \times w_{i-1}}$ y su salida como un elemento de $\mathbb{R}^{C_{i} \times h_{i} \times w_i}$. Decimos entonces que la capa $i$ tiene $C_{i-1}$ **canales de entrada**, $C_{i}$ **canales de salida**, y $h_{i-1}\times w_{i-1}$ y $h_i \times w_i$ son la **forma** de los mapas de entrada y salida, respectivamente. !!!ejemplo:Entradas de imágenes Si diseñamos una red neuronal para procesar imágenes en color de 1080p, entonces $C_0=3$ (las imágenes RGB tienen 3 canales de color), $h_0=1080$ y $w_0=1920$, es decir, la entrada a la primera capa es un elemento en $\mathbb{R}^{3 \times 1080 \times 1920}$. Para una imagen monocroma necesitaríamos sólo 1 canal.  Una **capa de convolución** no es más que una capa de red especializada, por lo tanto sigue el mismo patrón de hacer primero una transformación lineal, luego añadir un sesgo y, finalmente, aplicar una función de activación. La función de activación en una CNN es normalmente una función $\operatorname{ReLU}$ o $\operatorname{max pooling}$ (o ambas). La parte lineal consistirá en tomar convoluciones de los mapas de entrada, pero hay varias formas de hacerlo, veremos dos de ellas. La primero, y más sencilla, se denomina **convolución monocanal** (también conocida como **convolución en profundidad**): asigna un kernel de cierto tamaño a cada canal de entrada y luego realiza la convolución de cada canal de entrada con cada kernel, lo que devuelve un número de mapas igual al número de canales de entrada; posteriormente, se toman combinaciones lineales puntuales de estos nuevos mapas para generar el número deseado de mapas de salida. !!!side:25 Donde $C$ es el número de canales de entrada, $h \times w$ la forma del mapa de entrada, $m \times m$ la forma del núcleo y $C'$ el número de canales de salida. !!!def:Convolución monocanal Sean $f \in \mathbb{R}^{C \times h \times w}$, $k \in \mathbb{R}^{C \times m \times m}$ y $A \in \mathbb{R}^{C' \times C}$ [25]. Entonces definimos $SCC_{k,A}(f) \in \mathbb{R}^{C' \times (h-m+1) \times (w-m+1)}$ como: \begin{equation*} \operatorname{SCC}_{k,A}(f)_{c',i_1,i_2} := \sum_{c=1}^C A_{c',c} \cdot (k_{c,\cdot,\cdot} \star f_{c,\cdot,\cdot}) \end{equation*} para cada $c' \in \{ 1, \ldots, C' \}$, $i_1 \in \{ 1,\ldots,h-m+1 \}$ y $i_2 \in \{ 1,\ldots, w-m+1 \}$. Esta operación permite que las entradas de la pila del kernel $k$ y la matriz $A$ sean entrenables, por lo que el número de parámetros entrenables es $C\cdot m^2+C' \cdot C$. La figura siguiente ofrece una visualización de cómo funciona la convolución monocanal.  Una forma alternativa de utilizar la convolución para construir un operador lineal es la **convolución multicanal** (también conocida como **convolución multicanal multi kernel**). En lugar de asignar un kernel a cada canal de entrada y luego tomar combinaciones lineales, asignamos un kernel a cada combinación de canales de entrada y salida. !!!side:26 Donde $C$ es el número de canales de entrada, $C'$ el número de canales de salida, $h \times w$ la forma del mapa de entrada y $m \times m$ la forma del kernel. !!!def:Convolución multicanal Sea $f \in \mathbb{R}^{C \times h \times w}$ y $k \in \mathbb{R}^{C' \times C \times m \times m}$. Entonces, definimos $MCC_{k}(f) \in \mathbb{R}^{C' \times (h-m+1) \times (w-m+1)}$ como: \begin{equation*} \operatorname{MCC}_{k}(f)_{c',i_1,i_2} := \sum_{c=1}^C k_{c',c,\cdot,\cdot} \star f_{c,\cdot,\cdot} \end{equation*} para cada $c' \in \{ 1, \ldots, C' \}$, $i_1 \in \{ 1,\ldots,h-m+1 \}$ y $i_2 \in \{ 1,\ldots,w-m+1 \}$. Bajo esta construcción, los componentes del núcleo son los parámetros entrenables y así tenemos un total de $C'\cdot C \cdot m^2$ parámetros entrenables. La construcción de convolución multicanal se ilustra en la siguiente figura:  !!!note Las convoluciones monocanal y multicanal son equivalentes en el sentido de que dada una instancia de una, siempre se puede construir una instancia de la otra que haga exactamente el mismo cálculo. En consecuencia, podemos trabajar con la construcción que prefiramos por el motivo que sea sin perder nada. Aunque las más frecuentes en la literatura son las convoluciones multicanal, Lo bueno de la convolución monocanal es que existe una clara separación entre el procesamiento realizado dentro de un canal en particular y la forma en que los canales de entrada se combinan para crear canales de salida. Estos dos pasos de procesamiento se fusionan en la operación de convolución multicanal, lo que hace que la técnica multicanal sea más difícil de razonar, ya que tener dos pasos distintos que hacen dos cosas distintas parece más elegante.  Todo lo que queda ahora para crear una capa CNN completa es combinar una de las operaciones de convolución, añadir padding si se desea y pasar el resultado a través de una operación de $\operatorname{max pooling}$ y/o una función de activación escalar como una $\operatorname{ReLU}$.  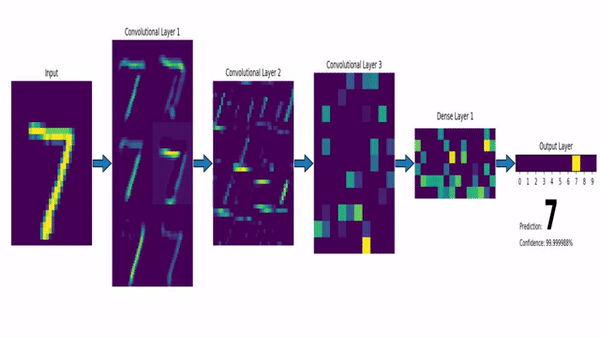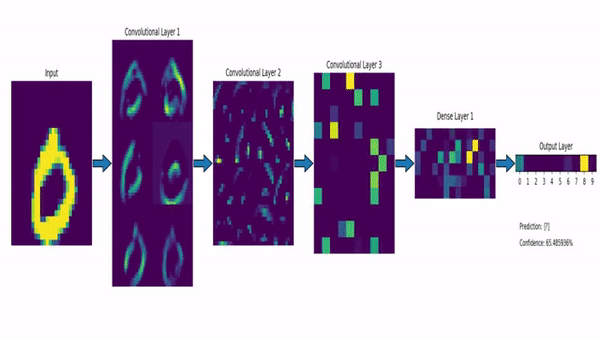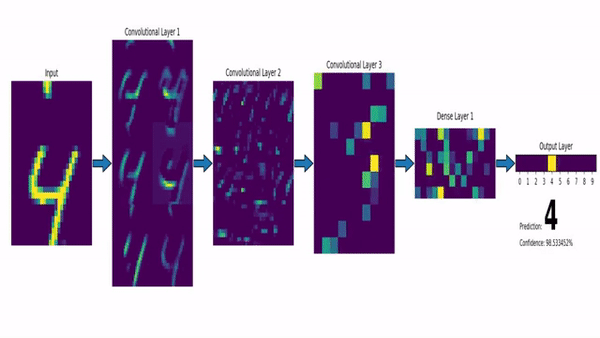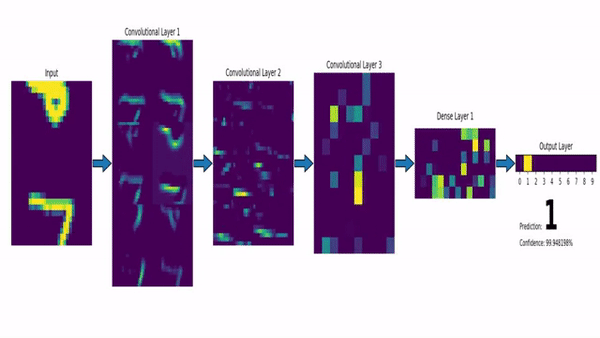!!!ejemplo: MNIST y LeNet-5 El conjunto de datos MNIST (Modified National Institute of Standards and Technology dataset) consiste en una gran colección de imágenes en escala de grises de $28\times 28$ de dígitos dibujados a mano. El objetivo es asignar a cada imagen la etiqueta 0-9 correcta. La red LeNet-5 proporciona una solución CNN a este problema. En la figura siguiente se puede ver una versión modernizada de la misma. La red clásica de [#lecun1998] utilizaba funciones de activación sigmoidales, capas de submuestreo inusuales y conexiones gaussianas, mientras que la actual hace uso de ReLUs, max pooling y capas totalmente conectadas, proporcionando una red algo más simple que funciona igual de bien.   # Diferenciación Automática y Retropropagación !!!side Ver esta [otra entrada](https://www.cs.us.es/~fsancho/Blog/posts/Diferenciacion_Automatica/) para una presentación ampliada sobre la Diferenciación Automática. Los mecanismos más habituales y efectivos para ajustar redes neuronales se basan en gradientes, por lo que la capacidad para entrenar una red va a depender fuertemente de cómo se calculen estos gradientes, tanto de su complejidad computacional como de su corrección. Para cualquiera que haya hecho un curso estándar de asignaturas matemáticas resultan naturales los siguientes enfoques (que podríamos denotar como *tradicionales*) para resolver este problema: 1. Calcular las fórmulas derivadas manualmente y codificarlas en el programa que implementa la red. 2. Utilizar un sistema de álgebra computacional para realizar la diferenciación simbólica y utilizar la fórmula resultante. 3. Utilizar la diferenciación numérica (es decir, diferencias finitas). El problema es que ninguna de estas tres opciones es atractiva: el cálculo manual de las derivadas para cada red que se defina es una opción inabordable (estamos hablando de cientos o miles de composiciones de funciones no lineales); la diferenciación simbólica con sistemas de álgebra computacional suele producir expresiones complejas, enormes y crípticas para los casos no triviales, que provocan que su evaluación posterior esté muy lejos de ser eficiente; y para redes con millones, o miles de millones, de parámetros, el cálculo de diferencias finitas implicaría tal cantidad de evaluaciones de la red que su uso sería inabordable computacionalmente (además del error acumulado que se podría producir en las aproximaciones sucesivas). Desde hace ya tiempo los investigadores de este tipo de redes se dieron cuenta de que hacía falta una vía alternativa, y se desarrolló lo que hoy en día se conoce como **Diferenciación Automática** (**AD**, también llamada **Diferenciación Algorítmica**). Aunque es una técnica muy general que tiene usos más allá del aprendizaje automático, nos limitaremos a examinarla en el contexto de las redes neuronales feed-forward, y debemos tener en cuenta que no se trata de una variedad de diferenciación simbólica ni de diferenciación numérica, aunque contenga elementos de ambas. ## Cálculo de Gradientes y Grafo de Computación Supongamos un caso muy simple inicial en el que tenemos una red $F:\mathbb{R}\times \mathbb{R}^2 \to \mathbb{R}$ que hace uso de dos parámetros, $a$ y $b$, y usamos una función de pérdida $\ell$. Nuestro objetivo es calcular: \begin{equation} \label{eq:a_b_derivatives} \left. \frac{\partial}{\partial a}\ell(F(x_0;a,b),y_0) \right\vert_{(a,b)} \quad \text{y} \quad \left. \frac{\partial}{\partial b}\ell(F(x_0;a,b),y_0) \right\vert_{(a,b)} \end{equation} es decir, las derivadas parciales con respecto a nuestros parámetros en sus valores actuales, ya que queremos optimizar $\ell$ respecto a estos parámetros. Para simplificar la notación vamos a introducir algunas convenciones: !!!side:27 A primera vista la derivada parcial de un número real con respecto a otro número real no tiene sentido, pero si utilizamos un número real en el cálculo de un segundo sí que tiene sentido preguntarse cómo de sensible es el valor del segundo con respecto al primero si lo cambiamos un poco. Por supuesto, esta sensibilidad no es otra cosa que la derivada parcial de la función utilizada en el cálculo del segundo valor evaluado en el primer valor. Pero como no nos interesan las derivadas parciales completas simplifica las cosas mantener implícita la función y sus derivadas parciales y utilizar la notación más sencilla que acabamos de introducir. !!!note Sea $f, g, h, k:\mathbb{R}^2 \to \mathbb{R}$ dadas por: \begin{equation} \label{eq:fghk} f(x,y) = g(h(x,y),k(x,y)) \end{equation} Evaluamos $f$ en un $(x,y)\in\mathbb{R}^2$ fijo calculando: \begin{equation*} u = h(x,y) , \quad v = k(x,y) , \quad z = g(u,v) = f(x,y) , \end{equation*} como notaciones que sirven, simultáneamente, para los valores intermedios/salida y para las funciones que dependen de los valores de entrada/intemedios. De esta forma, relajaremos la notación y usaremos las siguientes notaciones para los resultados intermedios $u$ y $v$ [27]: \begin{equation*} \begin{split} \frac{\partial u}{\partial x} &:= \left. \frac{\partial}{\partial x} h(x,y) \right|_{(x,y)} , \qquad \frac{\partial u}{\partial y} := \left. \frac{\partial}{\partial y} h(x,y) \right|_{(x,y)} , \\ \frac{\partial v}{\partial x} &:= \left. \frac{\partial}{\partial x} k(x,y) \right|_{(x,y)} , \qquad \frac{\partial v}{\partial y} := \left. \frac{\partial}{\partial y} k(x,y) \right|_{(x,y)} \end{split} \end{equation*} y para la salida final $z$: \begin{equation*} \begin{split} \frac{\partial z}{\partial u} &:= \left. \frac{\partial}{\partial u} g(u,v) \right|_{(u,v)} , \qquad \frac{\partial z}{\partial v} := \left. \frac{\partial}{\partial v} g(u,v) \right|_{(u,v)} \\ \frac{\partial z}{\partial x} &:= \left. \frac{\partial}{\partial x} f(x,y) \right|_{(x,y)} , \qquad \frac{\partial z}{\partial y} := \left. \frac{\partial}{\partial y} f(x,y) \right|_{(x,y)} \end{split} \end{equation*} Utilizando esta notación, la regla de la cadena aplicada a \eqref{eq:fghk} puede expresarse entonces como: \begin{equation} \label{eq:numeric_chain_rule} \frac{\partial z}{\partial x} = \frac{\partial z}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial x} \quad \text{and} \quad \frac{\partial z}{\partial y} = \frac{\partial z}{\partial u} \frac{\partial u}{\partial y} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial y} \end{equation} Abreviando aún más, introducimos la siguiente notación para las derivadas parciales de la pérdida: !!!side:28 Técnicamente, el valor del gradiente de la función de pérdida con respecto a $\alpha$ evaluado en el valor actual de $\alpha$, pero es demasiado largo y complicado decirlo así. !!!def Sea $\ell$ la función de pérdida y $a$ un parámetro o resultado intermedio utilizado en el cálculo de $\ell$, entonces escribimos: \begin{equation*} \overline{a} := \frac{\partial \ell}{\partial a} \end{equation*} al que nos referimos como **gradiente** [28]. Como ejemplo para ver cómo funciona esta notación vamos a elegir un ejemplo concreto y sistemáticamente trabajar a través de su diferenciación: !!!side:29 Debe tenerse en cuenta que en estas notaciones usamos las variables simultáneamente como símbolos de variable y como los valores concretos que podrían tomar en cada evaluación del gradiente que sea necesaria. !!!ejemplo Sea $F(x;a,b):=\sigma(a x + b)$ para alguna elección de función de activación (diferenciable) $\sigma:\mathbb{R} \to \mathbb{R}$. Sea $(x_0,y_0) \in \mathbb{R}^2$ algún punto de datos y usemos la función de pérdida $\ell(y,y') = \frac{1}{2}(y-y')^2$. Para cada elección de valores de $a,b \in \mathbb{R}$, podemos calcular la pérdida correspondiente, siguiendo los pasos mostrados en el lado izquierdo de la siguiente figura:  Es lo que esto se llama el **paso adelante**. Tras la evaluación de la red, podemos empezar a calcular las derivadas parciales de la pérdida con respecto a los parámetros $a$ y $b$ aplicando la regla de la cadena de atrás hacia adelante, tal y como se muestra a la derecha de la figura. Es lo que se denomina el **paso hacia atrás** [29]. !!!side:30 Es precisamente en estos valores sombreados donde hacemos abuso de notación, ya que en el paso adelante se usan como valores numéricos, y en el paso atrás se han tratado parcialmente como variables y funciones intermedias. Algunas cosas a tener en cuenta sobre el esquema anterior son: * Todo lo que hemos escrito es un cálculo numérico y todo el esquema puede ser ejecutado por un ordenador sin cambios. * Al escribir el paso hacia atrás, hemos utilizado nuestro conocimiento simbólico de cómo las operaciones del paso hacia delante deben diferenciarse si consideramos las funciones asociadas. * Escribir $\overline{\ell}=1$ es, por supuesto, redundante, pero las implementaciones de autodiff realmente comienzan el paso hacia atrás creando un tensor de un solo elemento que contiene el valor $1$ (y hace que el esquema parezca simétrico). * Algunos de los valores intermedios calculados durante el paso hacia delante se reutilizan durante el paso hacia atrás (concretamente, en la figura estos valores se han sombreado en verde) [30]. !!!alg: Es aquí donde se puede comprobar que, en durante los cálculos de entrenamiento de una red neuronal, muchos de los resultados intermedios tienen que almacenarse temporalmente para poder realiza el paso hacia atrás. Esta es la razón por la que el entrenamiento de una red neuronal requiere mucha memoria. Nada de lo que hemos hecho en el ejemplo mostrado es novedoso, simplemente hemos hecho lo que haríamos normalmente si nos pidieran calcular estas derivadas parciales. Sólo que lo hemos escrito sistemáticamente de forma que podamos automatizarlo. La clave para generalizar y automatizar el cálculo que hemos visto en la sección anterior es dividirlo en operaciones primitivas y hacer un seguimiento de cómo se componen. !!!ejemplo Supongamos ahora la red $F(x;a,b):=\operatorname{ReLU}(a x + b)$ con función de pérdida $\ell(y,y'):= \frac{1}{2}(y-y')^2$ evaluada para algún punto de datos $(x_0,y_0) \in \mathbb{R}^2$ y valores de parámetros $a,b \in \mathbb{R}$. Para este caso, los pasos equivalentes dados en el ejemplo anterior quedarían como:  En el caso mostrado es bastante sencillo ya que cada valor intermedio sólo se utiliza en el siguiente paso es decir, $t_i$ sólo dependen de $t_{i-1}$ y los parámetros. En consecuencia $\overline{t_i}$ sólo depende de $\overline{t_{i+1}}$ y $t_i$. Un ejemplo más general que tiene una estructura un poco más complicada sería el siguiente: !!!ejemplo Supongamos ahora la red $F(x;a,b):=\operatorname{ReLU}(a x + b) + (a x + b)$. La figura siguiente muestra el mismo proceso, pero donde se han añadido las dependencias entre los resultados intermedios:  Como se puede observar en la figura, el grafo de dependencia de los gradientes $\overline{t_i}$ es el inverso (dependencias en sentido contrario) del grafo de dependencia de los valores $t_i$ añadiéndole algunas dependencias de los resultados del paso hacia delante (mostradas con trazos punteados). Por ejemplo, tanto los valores $t_3$ como $t_4$ dependen del valor $t_2$, por lo que $\overline{t_2}$ depende tanto de $\overline{t_3}$ como de $\overline{t_4}$ además del propio $t_2$. Esta doble dependencia hace que la regla de la cadena aplicada a $\overline{t_2}$ tenga dos términos, por supuesto esto se generaliza a múltiples dependencias. La construcción de este **Grafo de Computación** es exactamente la forma en que las librerías de aprendizaje automático implementan el cálculo de gradiente. Cada vez que se realiza una operación en uno o más tensores, se añade un nuevo nodo al grafo para registrar qué operación se ha realizado y de qué entradas depende la salida. De esta forma, cuando llega el momento de calcular el gradiente, el grafo se recorre de atrás hacia adelante. En general, la evaluación de una red neuronal (realmente, de cualquier cálculo) puede expresarse como un **Grafo de Computación** en el que cada nodo corresponde a una operación (**primitiva**). Para poder realizar el paso hacia atrás cada nodo necesita saber cómo calcular su(s) propia(s) derivada(s) parcial(es). Los ejemplos mostrados sólo utilizaban operaciones escalares simples, es el momento de explorar cómo implementar tanto el cálculo hacia delante como hacia atrás para una función general multivariante con valores vectoriales. !!!note Sea $F: \mathbb{R}^n \to \mathbb{R}^m$ un mapa diferenciable, $\mathbb{x}=[x_1 \cdots \ x_n]^T \in \mathbb{R}^n$ y $\mathbb{y}=[y_1 \cdots \ y_m]^T \in \mathbb{R}^m$ de modo que $\mathbb{y}=F(\mathbb{x})$. Sea $\ell \in \mathbb{R}$ la pérdida final calculada para una red neuronal que contiene $F$ como una de sus operaciones. Podemos generalizar nuestra notación gradiente de escalares a vector como: \begin{equation*} \overline{\mathbb{x}} := \frac{\partial \ell}{\partial \mathbb{x}} := \begin{bmatrix} \frac{\partial \ell}{\partial x_1} \\ \vdots \\ \frac{\partial \ell}{\partial x_n} \end{bmatrix} , \qquad \overline{\mathbb{y}} := \frac{\partial \ell}{\partial \mathbb{y}} := \begin{bmatrix} \frac{\partial \ell}{\partial y_1} \\ \vdots \\ \frac{\partial \ell}{\partial y_m} \end{bmatrix} \end{equation*} !!!def: Pasos Adelante y Atrás En las condiciones anteriores: Denominamos **paso hacia adelante** a la tarea de calcular $F: \mathbb{R}^n \to \mathbb{R}^m$: $\mathbb{x}\mapsto \mathbb{y}=F(\mathbb{x})$. Denominamos **paso hacia atrás** a la tarea de calcular $\overline{F}:\mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^n$: $(\mathbb{x}, \overline{\mathbb{y}}) \mapsto\overline{\mathbb{x}}$. !!!teorema:Teorema del Paso hacia atrás En las condiciones anteriores: $$\overline{F}(\mathbb{x}, \overline{\mathbb{y}}) =J(\mathbb{x})^T \overline{\mathbb{y}}$$ donde $J(\mathbb{x})$ es la matriz Jacobiana de $F$ evaluada en $\mathbb{x}$. !!!demo:Demostración \begin{align*} \overline{\mathbb{x}} &= \begin{bmatrix} \frac{\partial \ell}{\partial x_1} \\ \vdots \\ \frac{\partial \ell}{\partial x_n} \end{bmatrix} = \begin{bmatrix} \sum_{j=1}^m \frac{\partial \ell}{\partial y_j} \frac{\partial y_j}{\partial x_1} \\ \vdots \\ \sum_{j=1}^m \frac{\partial \ell}{\partial y_j} \frac{\partial y_j}{\partial x_n} \end{bmatrix} = \begin{bmatrix} \sum_{j=1}^m \overline{y_j} \, \frac{\partial y_j}{\partial x_1} \\ \vdots \\ \sum_{j=1}^m \overline{y_j} \, \frac{\partial y_j}{\partial x_n} \end{bmatrix} = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_1} \\ \vdots & & \vdots \\ \frac{\partial y_1}{\partial x_n} & \cdots & \frac{\partial y_m}{\partial x_n} \end{bmatrix} \begin{bmatrix} \overline{y_1} \vphantom{\frac{\partial y_1}{\partial x_1}} \\ \vdots \\ \overline{y_m} \vphantom{\frac{\partial y_1}{\partial x_1}} \end{bmatrix} = J(\mathbb{x})^T \overline{\mathbb{y}} \end{align*} Así que no es de extrañar que acabemos con la forma general de la regla de la cadena. ## Implementación de la operaciones Vamos a ver a continuación algunos ejemplos útiles de cómo se desarrollan estos dos pasos en funciones que se usan en Grafos de Computación habituales: !!!ejemplo:Suma punto a punto Sea $F:\mathbb{R}^2 \times \mathbb{R}^2 \to \mathbb{R}^2$ definida como $F(\mathbb{a},\mathbb{b}) := \mathbb{a} + \mathbb{b}$, con $\mathbb{a}=[a_1 \ a_2]^T$ y $\mathbb{b}=[b_1 \ b_2]^T$. Podemos definir $F$ equivalentemente como una función $F:\mathbb{R}^4 \to \mathbb{R}^2$ de la siguiente manera: \begin{equation*} \mathbb{c} = F(\mathbb{a},\mathbb{b}) = \begin{bmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{bmatrix} \begin{bmatrix} a_1 \\ a_2 \\ b_1 \\ b_2 \end{bmatrix} = \begin{bmatrix} a_1 + b_1 \\ a_2 + b_2 \end{bmatrix} \end{equation*} Como se trata de un operador lineal, la matriz jacobiana es simplemente la matriz constante que se usa como operador lineal, por lo que la operación hacia atrás $\overline{F}:\mathbb{R}^4 \times \mathbb{R}^2 \to \mathbb{R}^4$ viene dada entonces por: \begin{equation*} \begin{bmatrix} \overline{\mathbb{a}} \\ \overline{\mathbb{b}} \end{bmatrix} = \overline{F}(\mathbb{a},\mathbb{b},\overline{\mathbb{c}}) = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \overline{c_1} \\ \overline{c_2} \end{bmatrix} = \begin{bmatrix} \overline{c_1} \\ \overline{c_2} \\ \overline{c_1} \\ \overline{c_2} \end{bmatrix} = \begin{bmatrix} \overline{\mathbb{c}} \\ \overline{\mathbb{c}} \end{bmatrix} \end{equation*} para un gradiente $\overline{\mathbb{c}} = [c_1 \ c_2]^T \in \mathbb{R}^2$. Así que para implementar esta operación no tenemos que retener las entradas $\mathbb{a}$ y $\mathbb{b}$, podemos implementar el cálculo hacia atrás simplemente copiando el gradiente entrante $\overline{\mathbb{c}}$ y pasando las dos copias hacia arriba en el grafo. !!!ejemplo:Copia Sea $F:\mathbb{R}^n \to \mathbb{R}^{n}\times \mathbb{R}^{n}$ la función que hace dos copias de la entrada, concretamente: \begin{equation*} F(\mathbb{a}) = \begin{bmatrix} \mathbb{a} \\[4pt] \mathbb{a} \end{bmatrix} = \begin{bmatrix} a_1 \\ \vdots \\ a_n \\[2pt] a_1 \\ \vdots \\ a_n \end{bmatrix} = \begin{bmatrix} \mathbb{b} \\[4pt] \mathbb{c} \end{bmatrix} \end{equation*} con $\mathbb{a},\mathbb{b},\mathbb{c} \in \mathbb{R}^n$. Esta función es claramente lineal con Jacobiano: \begin{equation*} J = \begin{bmatrix} I_n \\[4pt] I_n \end{bmatrix} \end{equation*} donde $I_n$ es la matriz unidad de tamaño $n \times n$. Por lo que, dados los gradientes $\overline{\mathbb{b}},\overline{\mathbb{c}} \in \mathbb{R}^n$ de las salidas, el gradiente $\overline{\mathbb{a}}$ de la entrada se calcula como: \begin{equation*} \overline{\mathbb{a}} = \overline{F}(\mathbb{a},\overline{\mathbb{b}},\overline{\mathbb{c}}) = \begin{bmatrix} I_n & I_n \end{bmatrix} \begin{bmatrix} \overline{\mathbb{b}} \\[4pt] \overline{\mathbb{c}} \end{bmatrix} = \overline{\mathbb{b}} + \overline{\mathbb{c}} \end{equation*} !!!ejemplo:Producto Interior Sea $F:\mathbb{R}^{n}\times \mathbb{R}^{n} \to \mathbb{R}$ dada por: \begin{equation*} c = F(\mathbb{a},\mathbb{b}) = \sum_{i=1}^n a_i b_i \end{equation*} con $\mathbb{a}=[a_1 \ \cdots\ a_n]^T$ y $\mathbb{b}=[b_1 \ \cdots\ b_n]^T \in \mathbb{R}^n$. Entonces la matriz Jacobiana evaluada en $[\mathbb{a} \mathbb{b}]^T$ viene dada por: \begin{equation*} J(\mathbb{a},\mathbb{b}) = \begin{bmatrix} b_1 & \cdots & b_n & a_1 & \cdots & a_n \end{bmatrix} = \begin{bmatrix} \mathbb{b}^T & \mathbb{a}^T \end{bmatrix} \end{equation*} Dado un gradiente (escalar) $\overline{c} \in \mathbb{R}$ de la salida, calculamos los gradientes de $\mathbb{a}$ y $\mathbb{b}$ como sigue: \begin{equation*} \begin{bmatrix} \overline{\mathbb{a}} \\[4pt] \overline{\mathbb{b}} \end{bmatrix} = \overline{F}(\mathbb{a},\mathbb{b},\overline{c}) = \begin{bmatrix} \mathbb{b}^T & \mathbb{a}^T \end{bmatrix}^T \, \overline{c} = \overline{c} \, \begin{bmatrix} \mathbb{b} \\[4pt] \mathbb{a} \end{bmatrix} \end{equation*} que depende de los valores de entrada $\mathbb{a}$ y $\mathbb{b}$. En este ejemplo, el Jacobiano no es constante y tenemos que retener las entradas para poder hacer el paso hacia atrás. En los ejemplos de la sección anterior deconstruimos la función de pérdida $(y,y') \mapsto \frac{1}{2}(y-y')^2$ en tres operaciones primitivas. Como consecuencia, el paso hacia atrás tiene un paso en el que primero se multiplica por $2$ y luego se multiplica por $\frac{1}{2}$, esto no es eficiente, por supuesto. Por lo tanto, deconstruir nuestro cálculo en las operaciones más pequeñas posibles no siempre es aconsejable. En el siguiente ejemplo expresaremos la función de pérdida $L^2$ como una sola operación: !!!ejemplo:Pérdida $L^2$ Sea $F:\mathbb{R}^{n}\times \mathbb{R}^{n} \to \mathbb{R}$ dada por: \begin{equation*} \ell = F(\mathbb{y},\mathbb{y}') = \frac{1}{2} \sum_{i=1}^{n} (y_i - y_i')^2 \end{equation*} con $\mathbb{y}=[y_1 \ \cdots\ y_n]^T$ y $\mathbb{y}'=[y_1' \ \cdots\ y_n']^T \in \mathbb{R}^n$. Entonces la matriz Jacobiana evaluada en $[\mathbb{y} \mathbb{y}']^T$ viene dada por: \begin{equation*} J(\mathbb{y},\mathbb{y}') = \begin{bmatrix} y_1 - y_1' & \cdots & y_n - y_n' & y_1'-y_1 & \cdots & y_n'-y_n \end{bmatrix} = \begin{bmatrix} (\mathbb{y}-\mathbb{y}')^T & (\mathbb{y}'-\mathbb{y})^T \end{bmatrix} \end{equation*} La operación hacia atrás tiene signatura $\overline{F}:(\mathbb{R}^{n}\times \mathbb{R}^{n}) \times \mathbb{R} \to (\mathbb{R}^{n}\times \mathbb{R}^{n})$. El segundo argumento de $\overline{F}$ es un gradiente dado, $\overline{\ell} \in \mathbb{R}$, que es trivialmente $\overline{\ell}=1$ si la salida $\ell$ es la pérdida final que nos interesa minimizar. Por tanto: \begin{equation*} \begin{bmatrix} \overline{\mathbb{y}} \\[4pt] \overline{\mathbb{y}'} \end{bmatrix} = \overline{F}(\mathbb{y},\mathbb{y}',\overline{\ell}=1) = \begin{bmatrix} (\mathbb{y}-\mathbb{y}')^T & (\mathbb{y}'-\mathbb{y})^T \end{bmatrix}^T \, \overline{\ell} = \begin{bmatrix} \mathbb{y}-\mathbb{y}' \\[4pt] \mathbb{y}'-\mathbb{y} \end{bmatrix} \end{equation*} Si $\mathbb{y}$ es la salida de la red neuronal e $\mathbb{y}'$ es la salida esperada (conocida gracias al dataset), entonces sólo estamos interesados en $\overline{\mathbb{y}}$ y sólo calcularíamos $\mathbb{y}-\mathbb{y}'$. Esto es equivalente a la computación mostrada en los ejemplos de la sección anterior pero evita las multiplicaciones redundantes. # Algoritmos de aprendizaje adaptativo Recordemos el escenario general de los algoritmos de descenso por gradiente que nos han llevado hasta aquí: !!!alg Tenemos un espacio de parámetros $W = \mathbb{R}^N$ y algún valor de parámetro inicial $w_0 \in W$. Sea $I_t$ el lote en la iteración $t \in \mathbb{N}$ y $\ell_{I_t}$ su función de pérdida asociada. Abreviaremos el gradiente del lote actual como: \begin{equation*} g_t := \nabla \ell_{I_t} (w_t) \end{equation*} La regla de actualización SGD con **tasa de aprendizaje** $\eta>0$ es entonces: \begin{equation*} w_{t+1} = w_t - \eta g_t \end{equation*} Con el **momentum**, la regla de actualización pasa a ser: \begin{equation*} \begin{split} v_{t} &= \mu v_{t-1} - \eta g_t, \\ w_{t+1} &= w_t + v_t, \end{split} \end{equation*} donde $v_0 = 0$ y $\mu \in [0,1)$ es el **factor de momentum**. Pero no suficiente con ser capaces de calcular los gradientes, la tasa de aprendizaje usada en los algoritmos de descenso del gradiente es crucial para el éxito del proceso de entrenamiento. En general, la pérdida es muy sensible a algunos parámetros pero insensible a otros, basta pensar en los parámetros de las distintas capas. El *momentum* alivia algunos de los problemas pero introduce problemas propios y añade otro hiperparámetro que tenemos que afinar. Asignar a cada parámetro su propia tasa de aprendizaje (y ajustarla continuamente) no es factible. Lo que necesitamos son métodos automáticos. Esto ha llevado al desarrollo de **Algoritmos de Aprendizaje Adaptativo**. La idea es establecer la tasa de aprendizaje de forma dinámica por parámetro en cada iteración sobre la base de la historia de los gradientes. Vamos a ver tres de estos métodos: *Adagrad*, *RMSProp* y *Adam*, aunque hay una infinidad de variantes que se han probado y están disponibles en diversas librerías. ## Adagrad !!!side:31 Si consideramos las operaciones vectoriales como operaciones por componentes, entonces podemos escribir de forma más concisa: \begin{equation*} w_{t+1} = w_t - \frac{\eta}{\sqrt{\sum_{k=0}^t g_k^2 } + \varepsilon} g_t \end{equation*} **Adagrad** (**Adaptive Gradient Descent**) [#duchi2011] fue uno de los primeros métodos de tasa de aprendizaje adaptativo. La actualización de Adagrad se define para cada parámetro como [31]: \begin{equation*} \left( w_{t+1} \right)_i = \left( w_t \right)_i - \frac{\eta}{\sqrt{\sum_{k=0}^t \left( g_k \right)_i^2} + \varepsilon} \left( g_t \right)_i \end{equation*} En cada iteración ralentizamos la tasa efectiva de aprendizaje de cada parámetro individual por la norma $L^2$ de la historia de las derivadas parciales con respecto a ese parámetro. Como $(g_t)_i$ puede ser muy pequeño o cero, añadimos un pequeño $\varepsilon$ positivo ( por ejemplo, $10^{-8}$ o similar) para asegurar la estabilidad numérica (impidiendo la división por un número excesivamente pequeño). El beneficio de este método es que la elección de $\eta$ se vuelve menos importante, el tamaño del paso con el tiempo disminuirá hasta el punto de que puede establecerse en un mínimo local. Por otra parte, el denominador $\sqrt{\sum_{k=0}^t \left( g_k \right)_i^2}$ es monótono creciente y, finalmente, llevará el proceso de entrenamiento a una parada tanto si se ha alcanzado un mínimo local como si no. ## RMSProp **Root Mean Square Propagation** [#tieleman2012] (**RMSProp**) utiliza la misma idea básica que Adagrad, pero en lugar de acumular los gradientes al cuadrado utiliza una media ponderada de los gradientes históricos. Dado $\alpha \in (0,1)$ (que se denomina **factor de olvido**, **tasa de decaimiento** o **factor de suavizado**), definimos: \begin{equation*} \begin{split} v_{t} &= \alpha v_{t-1} + (1-\alpha) g_t^2 \\ w_{t+1} &= w_t - \frac{\eta}{\sqrt{v_t} + \varepsilon} g_t, \end{split} \end{equation*} donde, de nuevo, todas las operaciones aritméticas se aplican por componentes. Los valores sugeridos para empezar son $\eta=0,001$ y $\alpha=0,9$. ## Adam El método de **Estimación Adaptativa de Momentos** [#kingma2017] (**Adam**), además de almacenar una media exponencialmente decreciente de gradientes al cuadrado pasados, como RMSProp, también mantiene una media normal de los mismos, similar al *momentum*: Sea $\beta_1, \beta_2 \in (0,1)$, \begin{equation*} \begin{split} m_{t} &= \beta_1 m_{t-1} + (1-\beta_1) g_t , \\ v_{t} &= \beta_2 v_{t-1} + (1-\beta_2) (g_t)^2 , \end{split} \end{equation*} con $m_0 = v_0 = 0$. Los vectores $m_t$ y $v_t$ son estimaciones del primer momento (la media) y del segundo momento (la varianza no centrada), de ahí el nombre del método. Como empezamos con $m_0 = v_0 =0$ las estimaciones están sesgadas hacia cero, pero podemos medir cuán de sesgadas y si podemos corregir ese sesgo. Por inducción tenemos: \begin{equation*} \begin{split} m_t &= (1-\beta_1) \sum_{i=1}^t \beta_1^{t-i} g_i, \\ v_t &= (1-\beta_2) \sum_{i=1}^t \beta_2^{t-i} (g_i)^2, \end{split} \end{equation*} y, por tanto: \begin{equation*} \begin{split} \mathbb{E}[m_t] &= (1-\beta_1) \sum_{i=1}^t \beta_1^{t-i} \mathbb{E}[g_i], \\ \mathbb{E}[v_t] &= (1-\beta_2) \sum_{i=1}^t \beta_2^{t-i} \mathbb{E}[(g_i)^2]. \end{split} \end{equation*} Suponiendo que $\mathbb{E}[g_i]$ y $\mathbb{E}[(g_i)^2]$ son estacionarios (es decir, no dependen de $i$), obtenemos: \begin{equation*} \begin{split} \mathbb{E}[m_t] &= \left((1-\beta_1) \sum_{i=1}^t \beta_1^{t-i}\right) \mathbb{E}[g_t] &= (1-\beta_1^t) \mathbb{E}[g_t], \\ \mathbb{E}[v_t] &= \left((1-\beta_2) \sum_{i=1}^t \beta_2^{t-i} \right) \mathbb{E}[(g_t)^2] &= (1-\beta_2^t) \mathbb{E}[(g_t)^2]. \end{split} \end{equation*} Por tanto, los momentos corregidos por el sesgo son: \begin{equation*} \hat{m}_t = \frac{m_t}{1-\beta_1^t} , \qquad \hat{v}_t = \frac{v_t}{1-\beta_2^t} \end{equation*} La regla de actualización de Adam viene dada entonces por: \begin{equation*} w_{t+1} = w_t - \eta \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \varepsilon}, \end{equation*} donde, de nuevo, toda la aritmética se aplica por componentes. Los valores por defecto de los hiperparámetros sugeridos en el artículo original son $\eta=0,001$, $\beta_1=0,9$, $\beta_2=0,99$ y $\varepsilon=10^{-8}$. ## Qué variante usar Con esta variedad de métodos puede resultar complicado saber cuál usar en cada momento. Podemos dar algunas ideas generales: Si los datos son dispersos (algo que es habitual con datos de muy alta dimensión), entonces los métodos de tasa de aprendizaje adaptativa suelen superar al SGD simple (con o sin momentum). En [#kingma2017] se demuestra que, debido a su corrección de sesgo, Adam obtiene resultados ligeramente mejores al final del proceso de entrenamiento, por lo que es una opción segura para probar primero. No obstante, puede merecer la pena probar diferentes algoritmos para ver cuál funciona mejor para un problema determinado. !!!side:32 En las gráficas, las curvas de nivel más oscuras indican valores más bajos de la función.  La figura adyacente ilustra el diferente comportamiento de los métodos mostrados en algunos escenarios de pérdida artificiales. Estos escenarios modelan algunos de los problemas comunes que se pueden encontrar los algoritmos y muestran algunos de los puntos fuertes y débiles de cada método [32]: 1. **Canyon** muestra un parámetro con un gran efecto sobre la pérdida y un parámetro con poco efecto. 2. **Saddle** muestra un punto de silla prominente. 3. **Plateau** muestra una gran sección plana con un gradiente de fuga que hay que atravesar para llegar al mínimo. 4. En **Obstacle** se tiene un *obstáculo* que hay que rodear para llegar al mínimo. # Bibliografía [#bekkers2021]: Bekkers, Erik J (2021). B-Spline CNNs on Lie Groups. arXiv: 1909.12057 [cs.LG]. [#cohen2016]: Cohen, Taco and Max Welling (2016). “Group Equivariant Convolutional Networks”. In: International Conference on Machine Learning. PMLR, pp. 2990–2999. [#cohen2020]: Cohen, Taco, Mario Geiger, and Maurice Weiler (2020). A General Theory of Equivariant CNNs on Homogeneous Spaces. arXiv: 1811.02017 [cs.LG]. [#duchi2011]: Duchi, John, Elad Hazan, and Yoram Singer (2011). “Adaptive subgradient methods for online learning and stochastic optimization.” In: Journal of Machine Learning Research 12.7. [#federer2014]: Federer, Herbert (2014). Geometric Measure Theory. Springer. isbn: 978-3-540-60656-7. doi: 10.1007/978-3-642-62010-2. [#fukushima1987]: Fukushima, Kunihiko (1987). “Neural network model for selective attention in visual pattern recognition and associative recall”. Applied Optics 26.23, pp. 4985–4992. [#glorot2010]: Glorot, Xavier; Yoshua Bengio (2010). “[Understanding the difficulty of training deep feed forward neural networks](https://proceedings.mlr.press/v9/glorot10a.html)”. Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics. Ed. by Yee Whye Teh and Mike Titterington. Vol.9. Proceedings of Machine Learning Research. Chia Laguna Resort, Sardinia, Italy: PMLR, pp. 249–256. [#golan1999]: Golan, Jonathan S. (1999). Semirings and their Applications. Dordrecht: Springer Netherlands. isbn: 978-90-481-5252-0. doi: 10.1007/78-94-015-9333-5. url: http://link.springer.com/10.1007/978-94-015-9333-5. [#he2015]: He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun (2015). Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. arXiv: 1502.01852 [cs.CV]. [#ivakhnenko1966]: Ivakhnenko, Aleksei Grigorevich; Valentin Grigorevich Lapa (1966). Cybernetic predicting devices. Tech. rep. Purdue Univ Lafayette Ind School of Electrical Engineering. [#kingma2017]: Kingma, Diederik P. and Jimmy Ba (2017). Adam: A Method for Stochastic Optimization. arXiv: 1412.6980 [cs.LG]. [#kolokoltsov1997]: Kolokoltsov, Vassili N. and Victor P. Maslov (1997). Idempotent Analysis and Its Applications. Dordrecht: Springer Netherlands. isbn: 978-90-481-4834-9. doi: 10.1007/978-94-015-8901-7. url: http://link.springer.com/10.1007/978-94-015-8901-7. [#krizhevsky2012]: Krizhevsky, Alex, Ilya Sutskever, Geoffrey E Hinton (2012). “[ImageNet Classification with Deep Convolutional Neural Networks](https://proceedings.neurips.cc/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf)”. Advances in Neural Information Processing Systems. Ed. by F. Pereira, C.J. Burges, L. Bottou, and K.Q. Weinberger. Vol. 25. Curran Associates, Inc. [#lecun1998]: LeCun, Yann; Léon Bottou; Yoshua Bengio; Patrick Haffner (1998). “Gradient-based learning applied to document recognition”. In: Proceedings of the IEEE 86.11, pp. 2278–2324. [#lecun1989]: LeCun, Yann; Bernhard Boser, John S Denker, Donnie Henderson, Richard E Howard, Wayne Hubbard, Lawrence D Jackel (1989).“Backpropagation applied to handwritten zipcode recognition”. Neural computation 1.4, pp. 541–551. [#lee2010]: Lee, John M. (2010). Introduction to Topological Manifolds. 2nd ed. Graduate Texts in Mathematics. Springer. isbn: 978-1-4419-7939-1. doi: 10.1007/978-1-4419-7940-7. [#lee2013]: Lee, John M. (2013). Introduction to Smooth Manifolds. 2nd ed. Graduate Texts in Mathematics. Springer. isbn: 978-1-4419-9981-8. doi: 10.1007/978-1-4419-9982-5_1. [#mcculloch1943]: McCulloch, Warren S; Walter Pitts (1943). “A logical calculus of the ideas immanent in nervous activity”. The bulletin of mathematical biophysics 5.4, pp. 115–133. [#oh2004]: Oh, Kyoung-Su; Keechul Jung (2004). “GPU implementation of neural networks”. Pattern Recognition 37.6, pp. 1311–1314. [#tao2011]: Tao, Terence (2011). An Introduction to Measure Theory. Vol. 126. Graduate Studies in Mathematics. American Mathematical Society. isbn: 978-1-4704-6640-4. doi: 10.1090/gsm/126. [#tieleman2012]: Tieleman, Tijmen, Geoffrey Hinton, et al. (2012). “Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude”. In: Coursera: Neural networks for machine learning 4.2, pp. 26–31. (insert ../menu.md.html here)