**Equivarianza**
!!!side:33
Por ejemplo, sería deseable la invariancia temporal para un sistema de predicción meteorológica.
Hay muchas aplicaciones en las que queremos que la red neuronal sea estable bajo ciertas modificaciones en los datos de entrada, como en las redes convolucionales orientadas a reconocimiento de objetos, en las que el resultado de la red (la etiqueta de salida) debe ser la misma bajo cambios como simetrías, traslaciones, escalas, etc. Aunque esta es la interpretación más visual, podemos encontrar simetrías *naturales* en la mayoría de las aplicaciones, incluso aunque los espacios de salida y entrada no sean interpretables visualmente [33].
!!!side:34
De hecho, podríamos pensar que el uso de correlaciones cruzadas en las redes convolucionales es una solución que intenta incluir en la propia arquitectura de la red una solución parcial a este problema.
Comúnmente, se ha conseguido esta invarianza creando modificaciones *adhoc* de los datos de entrada por medio de lo que se ha llamado **data augmentation**, por ejemplo, entrenando una red convolucional con versiones trasladadas, rotadas y escaladas de los datosets originales, y esperando que la invariabilidad se codifique en los parámetros aprendidos de la red de ese modo. El problema de esta aproximación *clásica* es que aumenta drásticamente el tiempo de entrenamiento y no garantiza el éxito, por lo que sería preferible diseñar la red de modo que fuera intrínsecamente invariante [34].

La simetría deseada puede no ser una invarianza real, ya que no se espera que la salida permanezca exactamente igual, sino que se transforme de alguna manera similar a la entrada. Algunos autores utilizan el término *invarianza* para denotar ambos casos, pero aquí vamos a utilizar el término *equivarianza* para referirnos a una transformación que debe mantener la salida, y reservaremos el término *invarianza* para el caso especial en el que la transformación debe mantener más propiedades de similitud.
Expresar muchas de estas simetrías en ciertos dominios es complicado, por ejemplo, en dominios discretos las rotaciones y traslaciones de una imagen ni siquiera están bien definidas a menos que la traslación mantenga la cuadrícula o la rotación sea en múltiplos de $90^\circ$. Para evitar estos problema, vamos a trabajar en entornos continuos y sólo discretizaremos cuando llegue el momento de aplicar los resultados finales sobre modelos concretos. Para las imágenes, en lugar de representarlas como elementos de $\mathbb{R}^{H \times W}$ las representaremos como elementos de $C_c^\infty(\mathbb{R}^2)$, es decir, funciones suaves con soporte compacto.
El primer objetivo práctico para esta sección será construir un tipo de CNN que no sólo sea equivariante por traslación sino también por rotación. Pero como matemáticos que somos, queremos ser generales y desarrollar una teoría que permita también otras transformaciones, lo que nos llevará de forma natural a la teoría de los **Grupos de Lie**, que son esencialmente grupos de transformación continua.
Esta teoría desempeña un importante papel en muchos campos de estudio dispares, que van desde el análisis geométrico de imágenes hasta la física de partículas, pasando por la visión por ordenador, las matemáticas financieras, la robótica, etc. En las próximas secciones construiremos un marco general basado en los grupos de Lie que podrá verse como una receta general para construir una red neuronal que sea equivariante con respecto a un grupo de transformación arbitrario: la llamada CNN Equivariante por Grupos [#cohen2016] [#cohen2020], o **G-CNN** para abreviar.
# Variedades
El objeto matemático que será de utilidad para definir el concepto de invarianza aplicado a redes neuronales es el de **variedad**.
!!!side:35
Aunque estamos acostumbrados a hacer análisis en $\mathbb{R}^n$, sabemos que hay espacios no euclidianos de importancia similar y en los que podemos trabajar de forma similar.
Intuitivamente, una variedad representa la estructura matemática mínima que debe tener un conjunto para poder ser analizado con las herramientas que tenemos. En cierta forma, se define extrayendo qué partes de un espacio como $\mathbb{R}^n$ son necesarias para poder aplicar el mismo tipo de herramientas y resultados.
!!!ejemplo
Un ejemplo clásico es el círculo unitario $S^1$, que es claramente no euclidiano pero admite derivadas, integrales, EDP, etc. Cuando trabajamos con un objeto como $S^1$ solemos hacerlo indirectamente parametrizándolo de alguna manera, como por ejemplo con un ángulo $\theta \in [0,2 \pi)$, de forma que al menos localmente se parezca a $\mathbb{R}$.
Podemos generalizar esta idea y considerar todos los espacios que podamos, al menos localmente, identificar con un subconjunto de $\mathbb{R}^n$.
Quizás, la forma más adecuada de introducir las variedades es empezar con un conjunto minimal y poco a poco añadir capas de estructura que posibilitan aplicar herramientas más potentes (es como se hace, por ejemplo, en [#lee2010] y [#lee2013]).
!!!side:36
Aunque es un lema, para nosotros se comporta como una definición.
Como todo el proceso de construcción está perfectamente desarrollado en esas referencias, vamos a saltarnos algunos pasos y dar directamente una caracterización que resume en forma de lema las propiedades necesarias para trabajar con las estructuras necesarias, que no solo serán variedades, sino **variedades suaves** [36]:
!!!side:37
$I$ es un conjunto de índices.
(1)+(2): $M$ es localmente como $\mathbb{R}^n$.
(3): Además, podemos hacer que todo sea suave (como $\tau_{\alpha,\beta}: \mathbb{R}^n \to \mathbb{R}^n$, sabemos exactamente lo que significa que estos mapas sean suaves).
(5): Las cartas mantienen la separabilidad de $M$.
!!!teorema:Lema de las Cartas de Variedades Suaves
Sea $M$ un conjunto. Diremos que $M$ es una **variedad suave $n$-dimensional** si existe $\left\{ \left( U_\alpha, \varphi_\alpha \right) \right\}_{\alpha \in I}$, con $\{ U_\alpha \}_{\alpha \in I}\subseteq \cal{P}(M)$, y $\varphi_\alpha:U_\alpha \to \mathbb{R}^n$, verificando:
1. Para todo $\alpha \in I$, $\varphi_\alpha$ es una biyección entre $U_\alpha$ y un subconjunto abierto de $\mathbb{R}^n$.
2. Para cada $\alpha,\beta \in I$, los conjuntos $\varphi_\alpha \left( U_\alpha \cap U_\beta \right)$ y $\varphi_\beta \left( U_\alpha \cap U_\beta \right)$ son abiertos en $\mathbb{R}^n$.
3. Si $U_\alpha \cap U_\beta \neq \varnothing$ entonces la aplicación $\tau_{\alpha,\beta} := \varphi_\beta \circ \varphi_\alpha^{-1} : \varphi_\alpha(U_\alpha \cap U_\beta) \to \varphi_\beta(U_\alpha \cap U_\beta)$ es suave [37].
4. Existe $J \subset I$ numerable (puede ser finito) de modo que $\bigcup_{\alpha \in J} U_\alpha = M$, es decir, existe un recubrimiento numerable de $M$.
5. Si $p_1, p_2\in M$, $p_1\neq p_2$, entonces existen $U_\alpha$ y $U_\beta$ (no necesariamente distintos) y $V \subset U_\alpha$ y $W \subset U_\beta$, disjuntos, tales que $\varphi_\alpha(V)$ y $\varphi_\beta(W)$ son abiertos en $\mathbb{R}^n$, y $p_1 \in V$ y $p_2 \in W$.
!!!def: Cartas y Atlas
Decimos que cada par $\left( U_\alpha, \varphi_\alpha \right)$ es una **carta** (**suave**) y que el conjunto $\left\{ \left( U_\alpha, \varphi_\alpha \right) \right\}_{\alpha \in I}$ es un **atlas** (**suave**) de $M$.
Los mapas $\tau_{\alpha,\beta} := \varphi_\beta \circ \varphi_\alpha^{-1}$ se denominan **mapas de transición** del atlas.
Las cartas que tienen mapas de transición suaves en ambos sentidos se dice que son **compatibles**.

!!!side:38
En el ejemplo del círculo unitario que veremos a continuación esta distinción quedará clara ya que podemos ver que podemos construir cualquier cantidad de atlas que describan la misma variedad.
!!!note: La variedad *no es* el atlas
En el Lema anterior decimos que el conjunto $M$ junto con un atlas $\left\{ \left( U_\alpha, \varphi_\alpha \right) \right\}_{\alpha \in I}$ *da* una variedad suave en lugar de afirmar que *es* una variedad suave. Esto se debe a que podríamos construir otro atlas compatible con el primero, pero el conjunto junto con el nuevo atlas seguirían describiendo la misma variedad [38].
!!!def:Atlas compatibles y máximos
Decimos que dos atlas son **compatibles** si los mapas de transición entre cartas de los dos atlas son también suaves, si dos atlas son compatibles describen la misma variedad.
Formalmente, podríamos definir una variedad suave como la clase de equivalencia de todos los atlas según el Lema anterior bajo la relación de equivalencia de que los atlas son compatibles.
También podríamos considerar la unión de todos los atlas compatibles posibles, denominada **atlas máximo**, como definitoria de la variedad.
!!!note: Separabilidad
El punto (5) del Lema anterior garantiza que una variedad es un espacio de Hausdorff ($T_2$-separable), esto significa simplemente que para dos puntos distintos $p_1$ y $p_2$ podemos encontrar vecindades de ambos que sean disjuntas (una vecindad en la variedad es una preimagen de una vecindad en una carta).
Se pueden construir ejemplos que satisfagan (1)-(4) pero no (5), por lo que la separabilidad hay que pedirla adicionalmente.
La propiedad de separabilidad de Hausdorff es necesaria, entre otras cosas, para que los límites sean únicos.
Definimos lo que son los **subconjuntos abiertos** de la variedad mirando sus imágenes en $\mathbb{R}^n$.
!!!side:39
Definimos la topología de $M$ a partir del atlas y de la topología estándar en $\mathbb{R}^n$.
!!!def:Topología en $M$
Un subconjunto $V \subset M$ es abierto si $\varphi_\alpha \left( V \cap U_\alpha \right)$ es abierto en $\mathbb{R}^n$ para todo $\alpha \in I$ [39].
Con esta definición podríamos reformular el punto (5) del Lema como:
!!!alg
$M$, con la topología inducida por el atlas, es separable Hausdorff.
Por supuesto si $\left( U_\alpha, \varphi_\alpha \right)$ es una carta entonces si $V \subset U_\alpha$ es abierto entonces $\left( V, \varphi_\alpha\vert_V \right)$ también es una carta.
!!!note:Conjuntos abiertos y cartas continuas
Definir los conjuntos abiertos de $M$ como las preimágenes de subconjuntos abiertos de $\mathbb{R}^n$ hace que las cartas sean mapas continuos por definición.
Puede darse el caso de que cuando estemos construyendo una variedad no empecemos con $M$ siendo sólo un conjunto.
Por ejemplo, en muchos casos empezamos con que $M$ es un subconjunto de $\mathbb{R}^n$, en ese caso ya sabemos cuáles son los subconjuntos abiertos de $M$ (es decir, ya se conoce la topología de $M$).
Si ya hemos decidido cuáles van a ser los subconjuntos abiertos de $M$ entonces tenemos que asegurarnos de que las dos nociones de *abierto* coinciden.
Esto requiere que las cartas sean mapas continuos por construcción en lugar de ser continuos por definición.
!!!ejemplo:El Círculo Unidad
 Sea $S^1$ el círculo unidad en $\mathbb{R}^2$, es decir, $S^1 = \left\{ (x,y) \ \middle\vert\ x^2+y^2=1 \right\}$. Entonces podemos construir dos cartas suaves que cubren $S^1$:
$$
\begin{align*}
& U_1 = S^1 \setminus \left\{ \left(-1,0\right) \right\},\quad \varphi_1(x,y): U_1 \to (-\pi,\pi),
\\
& U_2 = S^1 \setminus \left\{ \left( 1,0 \right) \right\},\quad \varphi_2(x,y): U_2 \to (0,2\pi)
\end{align*}
$$
donde $\varphi_1$ da el ángulo entre el eje $X$ y $(x,y)$ medido de $-\pi$ a $\pi$ y $\varphi_2$ da ese mismo ángulo medido de $0$ a $2 \pi$.
Claramente $U_1 \cup U_2 = S^1$ y vemos que $\varphi_1(U_1)=\left(-\pi,\pi\right)$ y $\varphi_2(U_2)=\left(0,2\pi \right)$, por lo que estas dos cartas forman un atlas de $S^1$. Ahora tenemos que comprobar los mapas de transición, tengamos en cuenta que $U_1 \cap U_2 = S^1 \setminus \left\{ (-1,0), (1,0) \right\}$ que consta de dos componentes disjuntas, por lo que el mapa de transición de la primera a la segunda carta tendría como dominio $(-\pi,0) \cup (0,\pi)$ y se definiría como:
\begin{equation*}
\tau_{1,2} (\theta) = \varphi_2 \circ \varphi_1^{-1} (\theta)
=
\begin{cases}
\theta & \text{ if } \theta \in (0,\pi),
\\
\theta + 2 \pi & \text{ if } \theta \in (-\pi,0),
\end{cases}
\end{equation*}
que es suave en su dominio (la discontinuidad en $\theta=0$ no es parte del dominio). De forma similar, se puede comprobar sencillamente que $\tau_{2,1}$ es igualmente suave.
Toda la construcción se visualiza en la figura, con los mapas de transición representados con el sombreado gris.
## Mapas Suaves
Una razón importante para introducir las variedades suaves es poder hablar de mapas suaves. Aunque los términos **mapa** y **función** son técnicamente intercambiables utilizaremos el término **función** para mapas cuyo codominio es $\mathbb{R}$ o $\mathbb{R}^k$ y utilizaremos **mapa** para funciones entre entre variedades generales.
!!!def:Mapas Suaves
Sean $M$ y $N$ dos variedades suaves y sea $F:M \to N$ un mapa cualquiera. Decimos que $F$ es un **mapa suave** si para cada $p \in M$ existe una carta suave $\left( U, \varphi \right)$ de $M$ que contiene a $p$ y una carta suave $\left( V, \psi \right)$ de $N$ que contiene $F(p)$ de modo que $F(U) \subseteq V$ y el mapa $\psi \circ F \circ \varphi^{-1}$ es suave de $\varphi(U)$ a $\psi(F(U)) \subseteq \psi(V)$.
 La figura adyacente representa visualmente esta definición.
Debido a la estructura suave (es decir, todos sus posibles atlas) con que está dotada una variedad suave esta definición es independiente de la elección de las cartas, la suavidad de los mapas de transición asegura esta propiedad clave.
La definición deja claro que sólo podemos hablar de suavidad de los mapas si las variedades en cuestión tienen estructuras suaves, de modo que cuando decimos que $F:M \to N$ es un mapa suave implicamos que $M$ y $N$ son variedades suaves aunque no especifiquemos ese hecho explícitamente.
Dos casos particulares de mapas suaves serán:
* **Función suave**: un mapa suave de $M$ a $\mathbb{R}$ o $\mathbb{R}^k$.
* **Curva suave**: un mapa suave de $\mathbb{R}$ (o algún intervalo de $\mathbb{R}$) a otra variedad suave.
!!!ejemplo
El mapa $F:\mathbb{R} \to S^1$ dado por $F(\theta):=\left( \cos\theta,\, \sin\theta \right)$ es una curva suave desde la variedad $\mathbb{R}$ a la variedad $S^1$.
!!!def:Difeomorfismo
Sean $M$ y $N$ variedades suaves, un mapa biyectivo suave de $M$ a $N$ que tiene un inverso suave se llama un **difeomorfismo**. Dos variedades entre las que existe un difeomorfismo se dice que son **difeomorfas**.
!!!ejemplo
El círculo unitario $S^1$ no es difeomorfo con $\mathbb{R}$ ya que no existe una biyección continua entre ambos.
Sin embargo, el círculo unitario es difeomorfo con el grupo $\operatorname{SO}(2)$ (es decir, el grupo de matrices ortogonales $2 \times 2$ con determinante 1) mediante la identificación:
\begin{equation*}
S^1 \ni
(x,y)
\qquad
\leftrightarrow
\qquad
\begin{bmatrix}
x & -y
\\
y & x
\end{bmatrix}
\in
\operatorname{SO}(2)
\end{equation*}
usualmente parametrizado con $\theta \in \mathbb{R}/(2\pi\mathbb{Z})$ como:
\begin{equation*}
S^1 \ni
(\cos\theta,\sin\theta)
\qquad
\leftrightarrow
\qquad
\begin{bmatrix}
\cos\theta & -\sin\theta
\\
\sin\theta & \cos\theta
\end{bmatrix}
\in
\operatorname{SO}(2)
\end{equation*}
# Grupos de Lie
## Definiciones Básicas
Para dar suficiente soporte a las herramientas que necesitamos desarrollar en Deep Learning, será conveniente dotar a las variedades de operaciones internas que verifican suficientes propiedades, y ese es precisamente el papel que juegan los Grupos de Lie (un caso particular de grupo):
!!!side:40
Cuando no haya confusión, el producto de dos elementos, $g_1, g_4\in G$, lo notaremos como $g_1 g_2$.
!!!def: Propiedades de Grupos
Recordemos que un conjunto $G$, dotado de una operación interna (denominada habitualmente **producto** o **multiplicación** [40]) es un **Grupo Algebraico** si verifica ciertas propiedades. Estamos interesados en que, al menos, se verifiquen las siguiente:
* **Cierre**: $\forall g_1, g_2 \in G: g_1 g_2 \in G.$
* **Asociatividad**: $\forall g_1,g_2,g_3 \in G: (g_1 g_2) g_3=g_1 (g_2 g_3)$.
* **Elemento unidad**: $\exists e \in G, \forall g \in G: e g=g e=g$ y este elemento $e$ es único.
* **Inversa**: $\forall g \in G \ \exists g^{-1} \in G: gg^{-1}=g^{-1}g=e$.
Cuando, además de ser grupo, tenemos que es una variedad suave en la que la operación interna de grupo se comporta bien con las cartas, estamos ante un Grupo de Lie:
!!!def:Grupos de Lie
Un grupo de Lie, $G$, es una variedad suave que también es un grupo algebraico y en el que el producto y la inversa son mapas suaves:
\begin{equation*}
G \times G \to G, \quad (g_1,g_2) \mapsto g_1 g_2
\end{equation*}
\begin{equation*}
G \to G, \qquad\quad g \mapsto g^{-1}
\end{equation*}
Los grupos clásicos como los grupos lineales generales (los grupos de matrices que son invertibles) y especiales (los grupos de matrices que tienen determinante 1), el grupo ortogonal (el grupo de matrices ortogonales), etc. son ejemplos de grupos de Lie.
!!!note
Un grupo no tiene por qué ser conmutativo, de hecho los grupos de Lie particulares que más nos interesan no son conmutativos: tienen elementos de grupo $g_1,g_2$ para los que $g_1 g_2 \neq g_2 g_1$.
Por ello, para $g \in G$, denotamos por $L_g, R_g:G \to G$, $L_g(h)=gh$, $R_g(h)=hg$, las **multiplicaciones izquierda y derecha** (respectivamente) por $g$. A veces, también llamadas **traslaciones izquierda y derecha**.
!!!ejemplo:Ejemplos
1. $\mathbb{R}^n$ es un grupo de Lie (conmutativo) bajo adición vectorial $(\mathbb{x},\mathbb{y})\mapsto \mathbb{x}+\mathbb{y}$ y negación $\mathbb{x} \mapsto -\mathbb{x}$.
2. Grupo multiplicativo de números reales positivos: $\mathbb{R}_{> 0}$ es un grupo de Lie (conmutativo) bajo multiplicación $(x,y) \mapsto x y$ e inversión $x \mapsto \frac{1}{x}$.
3. El **Grupo Lineal General** de grado $n$, $\operatorname{GL}(n)$: es el grupo de todas las matrices invertibles $n \times n$. El producto del grupo es el producto de matrices.
4. El **Grupo Ortogonal Especial** de grado $n$, $\operatorname{SO}(n)$: es el subgrupo de $\operatorname{GL}(n)$ de todas las matrices con determinante $1$. Es el grupo de rotaciones en $n$ dimensiones. Para $SO(2)$ escribimos las matrices en términos del ángulo de la rotación $\theta \in \mathbb{R}/(2\pi\mathbb{Z})$ como
\begin{equation}
\label{eq:so2_matrix}
R(\theta) =
\begin{bmatrix}
\cos\theta & -\sin\theta
\\
\sin\theta & \cos\theta
\end{bmatrix}
\end{equation}
con la operación de grupo dada por $R(\theta_1) R(\theta_2)=R(\theta_1 + \theta_2)$.
5. El **Grupo Euclídeo Especial** de grado $n$, $\operatorname{SE}(n)$, es el grupo de rotaciones y traslaciones en $n$ dimensiones. Como conjunto es igual a $\mathbb{R}^n \times \operatorname{SO}(n)$ con la operación de grupo dada por:
\begin{equation}
\label{eq:se_law}
\left( \mathbb{x}_1, R_1 \right)
\left( \mathbb{x}_2, R_2 \right)
=
\left( \mathbb{x}_1 + R_1 \mathbb{x}_2,\, R_1 R_2 \right)
\end{equation}
La operación del grupo no es el producto directo (es decir, no es $\left( \mathbb{x}_1 + \mathbb{x}_2,\, R_1 R_2 \right)$) sino que el segundo grupo afecta a la operación del primer grupo. Llamamos a esto un **producto semidirecto**, para enfatizar esta diferencia escribimos $\operatorname{SE}(n)=\mathbb{R}^n \rtimes \operatorname{SO}(n)$.
!!!note
Como queremos diseñar una red neuronal que tome imágenes 2D y que sea equivariante por rotación-traslación, el grupo de Lie $\operatorname{SE}(2)$ es de especial interés para nosotros.
En el caso $\operatorname{SE}(2)$ podemos representar los elementos como $(\mathbb{x},R(\theta)) \in \mathbb{R}^2 \times \operatorname{SO}(2)$ con $R(\theta)$ la matriz de rotación de \eqref{eq:so2_matrix}, o como $(\mathbb{x},\theta) \in \mathbb{R}^2 \times [0,2\pi)$.
En este último caso, la ley de grupo puede escribirse como:
\begin{equation*}
(\mathbb{x}_1,\theta_1)
(\mathbb{x}_2,\theta_2)
=
\left(
\mathbb{x}_1 + R(\theta_1) \mathbb{x}_2
,\,
\theta_1 + \theta_2 \operatorname{mod}{2\pi}
\right)
\end{equation*}
Para que un subgrupo de un grupo de Lie sea también un grupo de Lie debe verificar que sigue comportándose bien respecto a las propiedades como variedad:
!!!teorema
Sea $G$ un grupo de Lie, entonces $H \subset G$ es un **subgrupo de Lie** de $G$ si:
1. $H$ es un subgrupo del grupo $G$.
2. $H$ es una subvariedad de la variedad $G$.
3. Las operaciones de grupo sobre $H$ son suaves.
!!!side:41
Se pueden encontrar los detalles y una demostración en [#lee2013].
Todo lo que rodea la definición formal y propiedades de las **subvariedades** cae más allá del alcance de esta entrada, pero el siguiente teorema proporciona una manera más fácil de identificar la mayoría de los subgrupos de Lie [41].
!!!teorema:Teorema del subgrupo cerrado de Cartan
Todo subgrupo de un grupo de Lie que sea cerrado (como conjunto) es un subgrupo de Lie.
No todos los subgrupos de Lie son cerrados, pero todos los que nos interesan sí lo son, por lo que podemos simplificar nuestro problema y considerar este teorema como método para demostrar si un subgrupo es un grupo de Lie.
!!!ejemplo:Ejemplos
1. Todo subespacio lineal de $\mathbb{R}^n$ es un subgrupo de Lie (cerrado) bajo adición vectorial.
2. Los grupos $\mathbb{R}^n \times \{ 0 \}$ y $\{ \mathbb{0} \} \times \operatorname{SO}(n)$ son subgrupos de Lie (cerrados) de $\operatorname{SE}(n)$.
## Acciones de grupo
El uso más importante de los grupos de Lie en la teoría de variedades consiste en la acción de un grupo de Lie sobre una variedad. Englobemos este uso dentro del contexto de las acciones:
!!!def:Acción de un grupo
Si $G$ es un grupo y $M$ un conjunto.
Una **acción izquierda** de $G$ sobre $M$ es una aplicación $G \times M \to M$ (escrito como $(g,p) \mapsto g \cdot p$) que satisface:
\begin{equation}
\begin{alignedat}{2}
g_2 \cdot (g_1 \cdot p)
&=
(g_2 g_1) \cdot p
\qquad
&&\forall g_1,g_2 \in G, p \in M
\\
e \cdot p &= p
&&
\forall p \in M
\end{alignedat}
\label{eq:left_action}
\end{equation}
Una **acción derecha** se define de forma similar como una aplicación $M \times G \to M$ que satisface:
\begin{equation*}
\begin{alignedat}{2}
(p \cdot g_1) \cdot g_2
&=
p \cdot (g_1 g_2)
\qquad
&&\forall g_1,g_2 \in G, p \in M
\\
p \cdot e &= p
&&
\forall p \in M
\end{alignedat}
\end{equation*}
Cuando $G$ y $M$ son variedades y el mapa es suave en ambas entradas entonces decimos que la acción es una **acción suave**.
!!!side:42
En cualquier caso, una acción derecha siempre puede convertirse en una acción izquierda definiendo $g \cdot p := p \cdot g^{-1}$, o viceversa para convertir una acción izquierda en una acción derecha.
Nos centraremos exclusivamente en las acciones izquierda, ya que \eqref{eq:left_action} nos permite interpretar la multiplicación de grupos con la composición de aplicaciones [42].
!!!alg
En nuestro contexto, $G$ será siempre un grupo de Lie (es decir, también una variedad) y $M$ siempre una variedad, y sólo consideraremos acciones suaves.
!!!note:Notación
A veces es conveniente etiquetar una acción, por ejemplo, $\rho:G \times M \to M$, y entonces la acción de un elemento de grupo $g$ sobre un punto $p$ puede escribirse entonces como: $$g \cdot p \equiv \rho(g,p) \equiv \rho_g(p)$$
Es fácil probar el siguiente resultado:
!!!teorema: Proposición
Si $\rho$ es una acción suave entonces para todo $g \in G$, $\rho_g : M \to M$ es un difeomorfismo ya que $\rho_{g^{-1}}$ es una inversa suave.
Una acción de grupo sobre una variedad induce una acción sobre cualquier espacio de funciones sobre esa variedad de forma directa:
!!!side:43
Por ejemplo, $X=C^k(M)$ o $X=L^p(M)$.
!!!teorema: Proposición
En las condiciones anteriores, si $\rho$ es una acción (izquierda) de $G$ sobre $M$, y $X$ es un espacio de funciones sobre $M$ [43], entonces la aplicación $\rho^X:G \times X \to X$, dada por:
\begin{equation}
\label{eq:induced_action}
(g,f) \qquad\mapsto \qquad
\left(\rho^X (g, f)\right)(p)
=
f(g^{-1}\cdot p)
=
f(\rho(g^{-1},p))
\end{equation}
es una acción (izquierda) de $G$ sobre $X$.
!!!demo:Demostración
Basta comprobar que: $\rho^X \left( g_2,\, \rho^X (g_1,\, f) \right) = \rho^X (g_2 g_1,\, f)$
\begin{align*}
&
\rho^X \left(
g_2
,\,
\rho^X (g_1,\, f)
\right)(p)
=
\rho^X(g_1,\,f)(g_2^{-1} \cdot p)
=
f \left( g_1^{-1} \cdot (g_2^{-1} \cdot p) \right)
=
f \left( (g_1^{-1} g_2^{-1}) \cdot p \right)
=
f \left( (g_2 g_1)^{-1} \cdot p \right)
=
\rho^X (g_2 g_1,\, f)(p)
\end{align*}
Esta acción sobre espacios de funciones tiene la propiedad adicional de que es lineal en el segundo argumento. A las acciones que, en general, tienen esta propiedad, les damos el nombre de **representaciones de los grupos de Lie**:
!!!def:Grupo de Automosfirmos
Recordemos que, dado un espacio vectorial, $V$, los automorfismos de $V$, $\operatorname{Aut}(V)$ es el conjunto de transformaciones lineales invertibles de $V$.
Pero no solo es un conjunto cualquiera, sino que forman grupo con la composición, por eso se le suele llamar **grupo de automorfismos**.
!!!def:Representación de grupos Lie
Sea $G$ un grupo de Lie y $V$ un espacio vectorial (de dimensión finita o no) entonces $\nu: G \to \operatorname{Aut}(V)$ es una **representación** de $G$ si es un homomorfismo suave, es decir, es suave y
\begin{equation*}
\nu(g_1 g_2) = \nu(g_1) \circ \nu(g_2)
\qquad
\forall g_1,g_2 \in G
\end{equation*}
!!!teorema:Proposición
De la definición se deduce que una representación $\nu$ también tiene las siguientes propiedades:
\begin{equation*}
\nu(e) = \mathrm{id}_V
\quad\text{y}\quad
\nu(g^{-1}) = \nu(g)^{-1}
\end{equation*}
!!!note
Como normalmente sólo tendremos una acción de grupo por cada variedad y, por tanto, una única representación correspondiente en un espacio de funciones dado, podemos sobrecargar el significado del símbolo "$\cdot$" y utilizar las siguientes notaciones equivalentes:
\begin{equation*}
g \cdot f := \rho^X_g(f) := \rho^X(g, f)
\end{equation*}
Así es como vamos a modelar la transformación que actúa sobre nuestros datos: por ejemplo, en el caso más sencillo, $f$ sería una imagen de entrada en $\mathbb{R}^2$ y $g \in \operatorname{SE}(2)$ sería una rotación-traslación que actúa sobre la imagen.
## Operadores y mapas equivariantes
!!!side:44
O más concisamente (utilizando la notación introducida en la última nota anterior):
\begin{equation*}
F(g \cdot p) = g \cdot F(p).
\end{equation*}
Supongamos que $G$ es un grupo de Lie, y $M$ y $N$ son dos variedades suaves con acciones (izquierda) suaves de $G$ sobre ellas, $\rho^M$ y $\rho^N$. Entonces, podemos considerar las aplicaciones $F:M \to N$ que *funcionan bien* respecto a dichas acciones de grupo, es decir, que verifican [44]:
\begin{equation*}
F(\rho^M(g,p)) = \rho^N (g,F(p)), \qquad \forall g \in G,\, \forall p \in M
\end{equation*}
!!!def:Aplicaciones Equivariantes
En las condiciones anteriores, $F$ es **equivariante** si el siguiente diagrama conmuta para cada $g \in G$:

Esta idea se extiende naturalmente a los operadores entre espacios de funciones sobre dichas variedades:
!!!def:Operador Equivariante
Sea $X$ un espacio de funciones sobre $M$, e $Y$ un espacio de funciones sobre $N$, ambos equipados con las correspondientes representaciones $\rho^X$ y $\rho^Y$ por \eqref{eq:induced_action}. Entonces un operador $A:X \to Y$ se dice **equivariante** si:
\begin{equation}
\label{eq:equivariant_operator}
A \circ \rho^X_g = \rho^Y_g \circ A, \qquad \forall g \in G
\end{equation}
O lo que es lo mismo: para cada elemento del grupo, realizar la transformación correspondiente en el espacio de entrada $X$ y luego aplicar el operador $A$ da el mismo resultado que aplicar primero el operador $A$ y luego realizar la transformación correspondiente al elemento del grupo en el espacio de salida $Y$. En este sentido, $F$ mantiene la estructura (respecto a la acción de $G$) entre ambas variedades.
!!!att
Nuestro objetivo en el entorno continuo es diseñar nuestra red neuronal como un operador equivariante que satisfaga \eqref{eq:equivariant_operator}. De esta forma, la red debe devolver el mismo resultado independientemente de las acciones que se tomen sobre los datos (y que consideramos que no deben modificar el resultado).
## Espacios homogéneos
Mientras que los grupos de Lie representan las transformaciones que nos interesan, los espacios homogéneos son los espacios en los que vivirán nuestros datos y sobre los que actuarán los grupos de Lie. Intuitivamente, un espacio es homogéneo (respecto a las acciones del grupo), si puedes moverte entre cualquier par de puntos por medio de las acciones del grupo.
!!!side:45
La propiedad transitiva se puede reformular como: para cada punto de $M$ existe un $g$ que nos lleva a cualquier otro punto de $M$.
!!!def:Espacio Homogéneo
Una variedad suave $M$ es un **espacio homogéneo** de un grupo de Lie $G$ si existe una acción (izquierda) suave $\rho:G \times M \to M$ que es **transitiva**, es decir:
\begin{equation*}
\forall p_1,p_2 \in M \ \exists g \in G: \rho(g,p_1)=g \cdot p_1=p_2
\end{equation*}
En estas condiciones, a los elementos de $M$ se les llama **puntos** del espacio homogéneo y a $G$ se le llama **grupo de movimientos** o **grupo fundamental** del espacio homogéneo [45].
!!!side:46
$\{0\}$ es una variedad. De hecho, todos los conjuntos finitos o numerables, $S$, son variedades de dimensión $0$: basta asignar a cada punto $p \in S$ su propia carta única $\varphi_p:\{ p \} \to \mathbb{R}^0=\{ 0 \}$. Como los dominios de estas cartas no se solapan, las cartas son trivialmente compatibles y forman un único atlas suave.
!!!ejemplo
Obsérvese que $G$ es un espacio homogéneo de sí mismo, llamado **espacio homogéneo principal**. La acción del grupo es sólo la multiplicación por la izquierda, es decir, $\rho_g = L_g$.
En el otro extremo tenemos el **espacio homogéneo trivial** formado por un único elemento $\{ 0 \}$, que es un espacio homogéneo de todo grupo de Lie bajo la acción identidad $\rho(g,0)=0$ [46].
!!!def:Estabilizador
Si $M$ es un espacio homogéneo de $G$, entonces para cada $p \in M$, el **estabilizador** (o **grupo de isotropía**) de $p$ es el subconjunto $G_p$ de $G$ (también denotado por $\operatorname{Stab}_G(p)$) que fija $p$, es decir:
\begin{equation}
\label{eq:stabilizer}
G_p
:=
\operatorname{Stab}_G(p)
:=
\left\{
g \in G \ \middle\vert\ g \cdot p = \rho(g,p) = p
\right\}
\end{equation}
!!!teorema: Teorema
Para cada $p\in M$, $G_p$ es un subgrupo de Lie de $G$.
!!!demo:Demostración
1. $G_p$ es subgrupo de $G$: Si $g_1,g_2 \in G_p$ entonces $(g_1 g_2) \cdot p = g_1 \cdot (g_2 \cdot p)=g_1 \cdot p=p$. Por tanto, $g_1 g_2 \in G_p$.
2. $G$ es cerrado: como la acción del grupo es suave, entonces si $\left( g_n \right)_{n\in\mathbb{N}}\subseteq G_p$ con $\lim_{n\to\infty} g_n = g \in G$ entonces $g \in G_p$, ya que:
\begin{equation*}
\rho(g,p)
=
\rho\left( \lim_{n\to\infty} g_n, p \right)
=
\lim_{n\to\infty} \rho(g_n,p)
=
p
\end{equation*}
Por tanto, por el Teorema del Subgrupo Cerrado de Cartan, $G_p$ es un subgrupo de Lie de $G$ para todo $p \in M$.
Cuando fijamos un elemento de referencia $p_0 \in M$, podemos definir el subconjunto $G_{p_0,p} \subset G$ de todos los elementos del grupo que asignan $p_0$ a $p$:
\begin{equation}
G_{p_0,p} := \left\{ g \in G \ \middle\vert \ g \cdot p_0 = p \right\}
\label{eq:homogeneous_set}
\end{equation}
En general, este conjunto no es un subgrupo (excepto para $G_{p_0,p_0}=G_{p_0}$):
!!!alg
Si $g_1,g_2 \in G_{p_0,p}$ entonces:
\begin{equation}
\label{eq:homogeneous_equivalence}
g_1 \cdot p_0 = g_2 \cdot p_0
\quad \Leftrightarrow\quad
g_1^{-1} g_2 \cdot p_0 = p_0
\quad \Leftrightarrow\quad
g_1^{-1} g_2 \in G_{p_0}.
\end{equation}
A pesar de que pueda parecer un inconveniente, esta condición impone una relación de equivalencia en $G$, que podemos establecer como cociente:
\begin{equation*}
G/G_{p_0}
:=
\left\{
S \subset G
\ \middle\vert\
\forall g_1, g_2 \in S: g_1^{-1} g_2 \in G_{p_0}
\right\}
=
\left\{
G_{p_0,p}
\ \middle\vert\
\forall p \in M
\right\}
\end{equation*}
Lo que nos permite dar un isomorfismo directo entre $M$ y $G/G_{p_0}$ dado por la aplicación que lleva $p \mapsto G_{p_0,p}$ (y cuya inversa lleva, obviamente, $G_{p_0,p} \mapsto G_{p_0,p} \cdot p_0$).
Obsérvese que esto es válido para cualquier espacio homogéneo de $G$. Es decir:
!!!teorema: Teorema
Si $M$ es un espacio homogéneo de $G$, entonces existe $H$ subgrupo de Lie cerrado de $G$ de forma que $M$ es isomorfo a $G/H$.
!!!side:47
Esto conduce a una notación concisa como $g \in p \Leftrightarrow g \cdot p_0 = p$ y la eliminación de la notación "$\cdot$" ya que si $p$ se ve como un subconjunto de $G$ entonces $g \cdot p \equiv g p$.
Por esta razón muchos autores desdibujan la línea entre un espacio homogéneo y su correspondiente cociente de grupo y equiparan efectivamente un punto del espacio homogéneo con su correspondiente clase de equivalencia en el grupo, es decir, $p \equiv G_{p_0,p}$ después de fijar un $p_0 \in M$ [47].
# Operadores Lineales
!!!side:48
El conjunto de funciones acotadas, $\operatorname{B}(M)$, es un *espacio de Banach* bajo la *norma del supremo* (también conocida como *norma $\infty$*) dada por $$\| f \|_\infty := \sup_{p \in M} |f(p)|$$
Ya estamos más cerca de poder extender las redes neuronales a este nuevo escenario. En lo que sigue, consideraremos una variedad de entrada, $M$, y una variedad de salida, $N$, que son espacios homogéneos de un mismo grupo de Lie $G$. Los datos de entrada serán una función acotada sobre $M$, $f \in X = \operatorname{B}(M)$, y se espera que la salida sea una función acotaba sobre $N$, un elemento de $Y = \operatorname{B}(N)$ [48].
Recordemos que la primera parte de una neurona artificial discreta está formada por un operador lineal $A:\mathbb{R}^n \to \mathbb{R}^m$, dado por:
\begin{equation*}
\left( A \mathbb{x} \right)_i
=
\sum_{j} (A)_{ij} x_i.
\end{equation*}
!!!side:49
Si $k_A \in \operatorname{B}(M \times N)$ y la aplicación $p \mapsto k_A(p,q)$ tiene soporte compacto para todo $q \in N$, entonces esta integral existe para todo $q \in N$ y, por tanto, $A$ es un operador lineal bien definido de $\operatorname{B}(M) \to \operatorname{B}(N)$. Aunque no todos los operadores lineales son de este tipo, como al final pensamos discretizar de todas formas, esta es una clase suficientemente amplia de operadores lineales que cubre nuestras necesidades.
Su análogo en el entorno continuo es un operador integral $A:\mathbb{R}^M \to \mathbb{R}^N$ de la forma:
\begin{equation}
\label{eq:integral_operator}
\left( A f \right)(q)
=
\int_M k_A (p,q) \, f(p) \, \d p
\end{equation}
donde la función $k_A:M \times N \to \mathbb{R}$ se denomina **kernel** del operador [49].
!!!note: Funciones Medibles
Técnicamente para que exista la integral de Lebesgue en \eqref{eq:integral_operator} el integrando tiene que ser medible.
No vamos a tratar con funciones no medibles y podemos suponer que cuando decimos función queremos decir función medible.
En este marco, en lugar de entrenar la matriz $A$, entrenaremos el kernel $k_A$. En la práctica no podemos entrenar una función continua, por lo que entrenar el kernel se reducirá a entrenar una discretización del mismo o a entrenar los parámetros de alguna parametrización suya.
Ahora todavía tenemos que especificar cómo vamos a integrar en un espacio homogéneo para avanzar.
## Medidas e Integración
!!!side:50
Para una introducción completa a la teoría de la medida, véase [#tao2011], aunque para nuestros propósitos es suficiente tener la idea intuitiva de que una medida permite evaluar el volumen de (ciertos) subconjuntos.
Las **medidas** son la generalización de conceptos como longitud, volumen, masa, probabilidad, etc. de manera que asigna un número real no negativo a subconjuntos de un espacio con el fin de que se comporte de forma similar a estos conceptos intuitivos. Cuando se definen medidas, a veces no es posible hacer que devuelvan valores sobre todos los posibles subconjuntos, y diferenciamos entre aquellos que son **medibles** y los que no [50].
Pero, al igual que hemos estado tratando anteriormente el tema de la coherencia entre estructuras (por ejemplo, entre una variedad y los grupos que pueden actuar sobre ella), podemos intentar añadir propiedades adicionales a las medidas con el fin de que mantengan cierta coherencia con estructuras previas del conjunto sobre el que se definen.
En este sentido, una **medida de Radon** sobre un espacio topológico de Hausdorff (recordemos, que tenga propiedades de separabilidad entre sus puntos) es una medida que se comporta bien con la topología del espacio: si una topología se define a partir de los abiertos y cerrados, las medidas de Radon deben estar definidas sobre éstos, debe ser finita sobre conjuntos compactos, etc.
La medida de Lebesgue es la medida de Radon invariante por traslación sobre $\mathbb{R}^n$ con la topología estándar, y coincide con la noción original de longitud/área/volumen de subconjuntos de $\mathbb{R}^n$:
!!!teorema: Proposición
Para todo $\mathbb{y} \in \mathbb{R}^n$ y funciones integrables $f:\mathbb{R}^n \to \mathbb{R}$ tenemos
\begin{equation}
\label{eq:translation_invariant_integral}
\int_{\mathbb{R}^n} f(\mathbb{x}-\mathbb{y}) \, \d\mathbb{x}
=
\int_{\mathbb{R}^n} f(\mathbb{x}) \, \d\mathbb{x}
\end{equation}
!!!side:51
Recuerda que en las variedades se infiere una topología, así que tiene sentido considerar las medidas de Radon asociadas a dicha topología, lo que nos permite conectar las medidas definidas con las cartas y las acciones del Grupo de Lie que definen la homogeneidad del espacio.
Idealmente, querríamos que la integración en un espacio homogéneo $M$ de un grupo de Lie $G$ se comportara de manera similar respecto a las acciones del grupo, es decir, para todo $g \in G$ nos gustaría:
\begin{equation}
\label{eq:group_invariant_integral}
\int_M \left( g \cdot f \right)(p) \, \d\mu_M(p)
:=
\int_M f(g^{-1} \cdot p) \, \d\mu_M(p)
=
\int_M f(p) \, \d\mu_M(p),
\end{equation}
para alguna medida de Radon $\mu_M$ en $M$ [51].
Esto impone una condición sobre la medida $\mu_M$, a saber: para todos los subconjuntos medibles $S$ de $M$ y $g \in G$ requerimos:
\begin{equation}
\label{eq:invariant_measure}
\mu_M(g\cdot S)=\mu_M(S).
\end{equation}
En otras palabras, necesitaríamos una medida (no nula) invariante por el grupo para obtener la integral deseada.
El problema es que estas medidas $G$-invariantes, o simplemente **medidas invariantes**, no siempre existen. Pero en algunos casos no todo está perdido, y todavía podemos obtener una **medida covariante**, que es una medida que satisface:
\begin{equation*}
\mu(g \cdot S)=\lambda\, \mu(S)
\end{equation*}
donde $\lambda >0$ mantiene ciertas propiedades respecto a las acciones de $g$.
!!!side:52
Es decir, la medida del conjunto transformado (por la acción) no tiene que mantenerse igual, pero la acción del grupo es coherente en esta transformación. Para cualesquiera $g_1,g_2 \in G$ y cualquier medible $S \subset M$:
\begin{equation*}
\chi(g_1 g_2)\, \mu(S)
=
\mu(g_1 g_2 \cdot S)
=
\mu(g_1 \cdot (g_2 \cdot S))
=
\\
\chi(g_1) \, \mu(g_2 \cdot S)
=
\chi(g_1) \, \chi(g_2) \, \mu(S)
\end{equation*}
!!!def: Carácter
Un **carácter multiplicativo** (**carácter lineal** o, simplemente, **carácter**) de un grupo de Lie $G$ es un homomorfismo continuo del grupo al grupo multiplicativo de los números reales positivos, es decir, $\chi:G \to \mathbb{R}_{>0}$ de modo que:
\begin{equation*}
\chi(g_1 g_2) = \chi(g_1)\, \chi(g_2) \qquad \forall g_1,g_2 \in G.
\end{equation*}
Si $M$ es un espacio homogéneo de $G$, entonces $\mu$ es una **medida covariante** si satisface:
\begin{equation}
\label{eq:covariant_measure}
\mu(g \cdot S)=\chi(g)\, \mu(S)
\end{equation}
para cualquier $g\in G$ y $S\subseteq M$ medible, donde $\chi$ es un carácter de $G$ [52].
Si integramos con respecto a una medida $G$-invariante decimos que tenemos una integral $G$-invariante, o simplemente una **integral invariante**, si la medida es covariante con un carácter $\chi$ decimos que tenemos una integral $\chi$-covariante o simplemente **integral covariante**.
!!!side:53
La integración es siempre con respecto a alguna medida. Si estamos integrando con respecto a $\mu$ entonces deberíamos escribir:
\begin{equation*}
\int_M \ldots\ \d \mu(p)
\end{equation*}
Pero como sólo consideraremos una medida por espacio sobre el que integramos lo abreviaremos como $\d p \equiv \d\mu(p)$.
!!!def:Integral Covariante
Sea $M$ un espacio homogéneo de un grupo de Lie $G$, decimos que la integral $\int_M \ldots \d p$ (usando alguna medida de Radon sobre $M$) es **covariante** con respecto a $G$ si existe un carácter $\chi_M$ de $G$ tal que
\begin{equation}
\label{eq:covariant_integral}
\int_M \left( g \cdot f \right) (p) \, \d p
=
\chi_M(g) \, \int_M f(p) \, \d p
\end{equation}
para todo $g \in G$ y todo $f:M \to \mathbb{R}$ para el que existe la integral (integrable) [53].
En el caso especial de que $\chi_M \equiv 1$ decimos que la integral es **invariante**.
!!!side:54
Llamada así por el matemático húngaro Alfréd Haar. Podemos decir *la* medida de Haar porque se puede probar que siempre existen y son únicas salvo multiplicación por una constante [#federer2014].
!!!ejemplo:Medidas e Integrales de Haar
Si $M=G$, entonces a *la* medida invariante se le llama **medida de Haar** (izquierda) en $G$ [54]. Por lo tanto, al integrar en el propio grupo siempre podemos hacer uso de una medida de Haar, $\mu_G$, de forma que se cumpla la siguiente igualdad:
\begin{equation}
\label{eq:invariant_group_integral}
\int_G \left( h \cdot f \right)(g) \, \d g
=
\int_G f(g) \, \d g
\qquad
\forall h \in G
\end{equation}
donde abreviamos $\d g := \d\mu_G(g)$.
También llamamos a esta integral invariante sobre el grupo **la integral (izquierda) de Haar**.
No todos los espacios homogéneos admiten una integral covariante, pero sí todos los que nos interesan. En adelante supondremos que todos los espacios homogéneos que consideremos admiten una integral covariante y que siempre podemos utilizar la igualdad \eqref{eq:covariant_integral}.
!!!side:55
Esto es intuitivamente fácil de entender: el área de un subconjunto de $\mathbb{R}^2$ es invariante bajo traslación y rotación.
!!!ejemplo:$G=\operatorname{SE}(2)$ y $M=\mathbb{R}^2$
Este es el caso más directo, el que se puede asociar al uso de CNN sobre imágenes,y tenemos la suerte de que la medida de Lebesgue sobre $\mathbb{R}^2$ es invariante con respecto a $G$ [55].
!!!ejemplo:Medida de Haar en $\operatorname{SE}(2)$
La medida de Haar en $\operatorname{SE}(2)$ también coincide (afortunadamente) con la medida de Lebesgue en $\mathbb{R}^2 \times [0,2\pi)$ cuando se utiliza la parametrización del Grupo Especial Euclídeo.
De hecho, si $g=(\mathbb{x}_1,\theta_1)$ y $h=(\mathbb{x}_2,\theta_2)$ entonces:
\begin{equation*}
\int_{\mathbb{R}^2} \int_{0}^{2\pi}
\left( (\mathbb{x}_1,\theta_1) \cdot f \right) (\mathbb{x}_2,\theta_2)
\, \d\theta_2 \,\d\mathbb{x}_2
=
\int_{\mathbb{R}^2} \int_{0}^{2\pi}
f \left( (\mathbb{x}_1,\theta_1)^{-1} (\mathbb{x}_2,\theta_2) \right)
\, \d\theta_2 \,\d\mathbb{x}_2
\end{equation*}
Haciendo el cambio de variable $(\mathbb{x}_3,\theta_3)=(\mathbb{x}_1,\theta_1)^{-1} (\mathbb{x}_2,\theta_2)$ obtenemos la siguiente matriz Jacobiana:
\begin{equation*}
\frac{\partial(x_2^1,x_2^2,\theta_2)}{\partial(x_3^1,x_3^2,\theta_3)}
=
\begin{pmatrix}
\cos\theta_1 & -\sin\theta_1 & 0
\\
\sin\theta_1 & \cos\theta_1 & 0
\\
0 & 0 & 1
\end{pmatrix}
\end{equation*}
que tiene determinante $1$.
En consecuencia, la integral de Haar (salvo constante multiplicativa) en $\operatorname{SE}(2)$ se puede calcular como:
\begin{equation}
\int_{\operatorname{SE}(2)} f(g) \, \d g
=
\int_{\mathbb{R}^2}
\int_0^{2\pi}
f(\mathbb{x},\theta)
\,
\d\theta
\d\mathbb{x}
\end{equation}
## Operadores Lineales Equivariantes
!!!side:56
Recordemos que el análogo continuo al operador lineal discreto de una neurona era un operador integral $A:\mathbb{R}^M \to \mathbb{R}^N$ de la forma:
\begin{equation*}
\left( A f \right)(q)
=
\int_M k_A (p,q) \, f(p) \, \d p
\end{equation*}
donde la función $k_A:M \times N \to \mathbb{R}$ se denomina **kernel** del operador.
Como nuestro objetivo es construir operadores equivariantes que puedan ayudar a entender y construir redes neuronales más eficientes, la pregunta más obvia que debemos hacernos es: ¿cuándo es un operador integral como el que se mostraba en \eqref{eq:integral_operator} equivariante? [56]
Recordemos que equivariante significa que:
\begin{equation*}
A (g \cdot f) = g\cdot(A f),\quad \forall\ g \in G,\ \forall\ f \in \operatorname{B}(M)
\end{equation*}
o, equivalentemente:
\begin{equation}
\label{eq:equivariant_A_2}
g^{-1} \cdot A (g \cdot f) = A f
\end{equation}
El siguiente resultado muestra cómo se traduce esta condición extra sobre $A$ en el kernel:
!!!teorema:Lema del Operador Lineal Equivariante
Sean $M$ y $N$ espacios homogéneos de un grupo de Lie, $G$, de modo que $M$ admite una integral covariante con carácter $\chi_M$.
Sea $A$ un operador integral de $\operatorname{C}(M) \cap \operatorname{B}(M) \to \operatorname{C}(N) \cap \operatorname{B}(N)$ con un kernel $k_A \in \operatorname{C}(M \times N)$ [56].
Entonces
\begin{equation*}
A(g\cdot f) = g \cdot (A f),\qquad \forall\ g \in G,\, \forall\ f \in \operatorname{C}(M) \cap \operatorname{B}(M)
\end{equation*}
si y solo si
\begin{equation}
\label{eq:equivariant_kernel_symmetry}
\chi_M(g) \, k_A(g \cdot p,g \cdot q)
=
k_A(p,q)
\qquad \forall\ g \in G,\ \forall\ p \in M,\ \forall\ q \in N
\end{equation}
Más aún, $A$ es acotado (y, por tanto, continuo) para la norma del supremo si
\begin{equation}
\label{eq:kernel_boundedness_requirement}
\sup_{q \in N} \int_{M} |k_A(p,q)| \d p < \infty
\end{equation}
!!!demo:Demostración
$\boxed{\Rightarrow}$: Supongamos que $A$ es equivariante, y tomemos $g \in G$ y $f \in \operatorname{C}(M) \cap \operatorname{B}(M)$ arbitrarias. La condición \eqref{eq:equivariant_A_2} para indica que:
$$(g^{-1} \cdot A (g \cdot f))(q) = (A f)q$$
Desarrollando la parte izquierda de esta igualdad:
$$(g^{-1} \cdot A (g \cdot f))(q) = g^{-1}\cdot(\int_M k_A(p,q) \, (g\cdot f) (p) \, \d p) = g^{-1}\cdot(\int_M k_A(p,q) \, f (g^{-1} \cdot p) \, \d p)$$
Esta última, como función de $q$, se puede escribir como:
$$\int_M k_A(p,g \cdot q) \, f (g^{-1} \cdot p) \, \d p$$
Por tanto, reescribiendo la parte derecha de la ecuación \eqref{eq:equivariant_A_2} como operador integral, obtenemos:
\begin{equation}
\label{eq:ELO_1}
\int_M k_A(p,g \cdot q) \, f (g^{-1} \cdot p) \, \d p
=
\int_M k_A(p,q) \, f(p) \,\d p
\end{equation}
para todo $q \in N$.
Fijemos $q \in N$ y sea $F(p):=k_A(g \cdot p, g \cdot q) f(p)$, entonces observemos que
\begin{equation*}
(g \cdot F)(p)
=
k_A(g \cdot g^{-1} \cdot p, g \cdot q) f(g^{-1} \cdot p)
=
k_A(p,g \cdot q) \, f (g^{-1} \cdot p)
\end{equation*}
que es el integrando izquierdo de \eqref{eq:ELO_1}.
Como hemos supuesto integración covariante utilizamos la Definición de Integral Covariante y tenemos
\begin{equation*}
\int_M \left( g \cdot F \right) (p) \, \d p
=
\chi_M(g) \, \int_M F(p) \, \d p
\end{equation*}
Aplicando esto a \eqref{eq:ELO_1} se obtiene
\begin{equation}
\label{eq:ELO_2}
\chi_M(g)
\int_M k_A(g \cdot p,g \cdot q) \, f (p) \, \d p
=
\int_M k_A(p,q) \, f(p) \,\d p
\end{equation}
Como $f$ es arbitrario y $p \mapsto k_A(p,q)$ es continua, se deduce que:
\begin{equation*}
\chi_M(g) \, k_A(g \cdot p,g \cdot q)
=
k_A(p,q)
\end{equation*}
para todo $p \in M$.
$\boxed{\Leftarrow}$: Supongamos ahora que $\chi_M(g) \, k_A(g \cdot p,g \cdot q)=k_A(p,q)$ para todo $g \in G$, $p \in M$ y $q \in N$. Entonces \eqref{eq:ELO_2} se obtiene para cualquier elección de $f \in \operatorname{C}(M) \cap \operatorname{B}(M)$, $g \in G$ y $q \in N$.
Sustituyendo la integral covariante en sentido contrario se obtiene
\eqref{eq:ELO_1}, lo que implica \eqref{eq:equivariant_A_2} ya que $q \in N$ es arbitraria.
La función $f$ y el elemento de grupo $g$ también se eligieron arbitrariamente, por lo que \eqref{eq:equivariant_A_2} se deduce para todo $f \in \operatorname{C}(M) \cap \operatorname{B}(M)$ y $g \in G$.
$\boxed{A \text{ acotado}}$: La acotación de $A$ se deduce de
\begin{align*}
\left\Vert A f \right\Vert_{\infty}
&=
\sup_{q \in N}
\left|
\int_M k_A(p,q) \, f(p) \d p
\right|
\\
&\leq
\sup_{q \in N}
\int_M
| k_A(p,q) | \, |f(p)| \d p
\\
&\leq
\left\Vert f \right\Vert_\infty
\cdot\
\sup_{q \in N}
\int_M | k_A(p,q) | \d p
\\
&
\overset{\eqref{eq:kernel_boundedness_requirement}}{<} \infty
\end{align*}
La condición \eqref{eq:kernel_boundedness_requirement} sobre el kernel es parcialmente redundante con el requisito de covarianza, como muestra el siguiente lema:
!!!Teorema:Lema
Bajo las condiciones del Lema del Operador Integral Equivariante, si el kernel $k_A \in \operatorname{C}(M \times N)$ satisface \eqref{eq:equivariant_kernel_symmetry} y \eqref{eq:kernel_boundedness_requirement} entonces:
\begin{equation*}
\left\Vert k_A(\ \cdot\ ,q_1) \right\Vert_{L^1(M)}
=
\left\Vert k_A(\ \cdot\ ,q_2) \right\Vert_{L^1(M)},
\qquad \forall\ q_1,q_2 \in N
\end{equation*}
!!!demo:Demostración
Como $N$ es un espacio homogéneo, entonces para todo $q_1,q_2 \in N$ existe un $g \in G$ de modo que $q_1 = g \cdot q_2$. Por tanto:
\begin{align*}
\int_M \left| k_A(p,q_1) \right| \d p
&=
\int_M \left| k_A(p,g \cdot q_2) \right| \d p
\\
&=
\int_M \left| k_A(g \cdot g^{-1} \cdot p, g \cdot q_2) \right| \d p
\\
\eqref{eq:equivariant_kernel_symmetry}
&=
\frac{1}{\chi_M(g)}
\int_M \left| k_A(g^{-1} \cdot p, q_2) \right| \d p
\\
\text{(Def. Integral Covariante)}
&=
\frac{\chi_M(g)}{\chi_M(g)}
\int_M \left| k_A(p, q_2) \right| \d p
\\
&=
\int_M \left| k_A(p,q_2) \right| \d p
\end{align*}
!!!note
La condición sobre el kernel del Lema del Operador Integral Covariante puede explotarse para expresarlo como una función sobre $M$ en lugar de $M \times N$:
Si fijamos $q_0 \in N$ y para cada $q \in N$ elegimos $g_q \in G_{q_0,q}$ (es decir, $g_q \cdot q_0=q$) entonces por \eqref{eq:equivariant_kernel_symmetry} tenemos que:
\begin{equation*}
k_A(p,q)
=
\chi_M(g_q^{-1}) \ k_A(g_q^{-1} \cdot p, g_q^{-1} \cdot q)
=
\chi_M(g_q^{-1}) \ k_A(g_q^{-1} \cdot p, q_0)
\end{equation*}
que fija la segunda entrada de $k_A$.
En consecuencia, podríamos contener toda la información de nuestro kernel en una función que existe sólo en $M$, como $\kappa_A(p) := k_A(p,q_0)$. Este núcleo reducido, $\kappa_A$, tiene todavía algunas restricciones para que el operador resultante sea equivariante, como precisa el siguiente teorema:
!!!teorema:Teorema: Operadores Lineales Equivariantes
Sean $M$ y $N$ espacios homogéneos de un grupo de Lie, $G$, de modo que $M$ admite una integral covariante respecto a un carácter $\chi_M$ de $G$.
Fijemos $q_0 \in N$ y sea $\kappa_A \in \operatorname{C}(M) \cap \operatorname{L}^1(M)$ *compatible*, es decir, que verifique:
\begin{equation}
\label{eq:kernel_compatibility}
\forall\ h \in G_{q_0}\ (h \cdot \kappa_A = \chi_M (h) \, \kappa_A)
\end{equation}
Entonces, el operador $A$ definido por
\begin{equation*}
(Af)(q) := \frac{1}{\chi_M(g_q)} \int_M (g_q \cdot \kappa_A) (p) \, f(p) \, \d p
\end{equation*}
donde para cada $q \in N$ podemos elegir $g_q$ de modo que $g_q \cdot q_0 = q$, es un *operador lineal acotado bien definido* de $\operatorname{C}(M) \cap \operatorname{B}(M) \to \operatorname{C}(N) \cap \operatorname{B}(N)$ que es *equivariante* con respecto a $G$.
Recíprocamente, todo operador integral equivariante con un núcleo $k_A \in \operatorname{C}(M\times N)$ y con $k_A(\,\cdot\,,q) \in \operatorname{L}^1(M)$ para algún $q \in N$ es de esta forma.
!!!demo:Demostración
$\boxed{\Rightarrow}$: Suponiendo que tenemos $\kappa_A \in \operatorname{C}(M) \cap \operatorname{L}^1(M)$ que satisface \eqref{eq:kernel_compatibility}.
Definimos $k_A \in C(M \times N)$ como:
\begin{equation*}
k_A(p,q) := \frac{1}{\chi_M(g_q)} (g_q \cdot \kappa_A)(p).
\end{equation*}
Entonces $k_A$ está bien definido ya que no depende de la elección de $g_q$ para un $q \in N$ dado.
Si $g_q'$ es otro elemento de grupo con $g_q \cdot q_0 = q$ entonces existe $h \in G_{q_0}$ tal que $g_q' = g_q h$, podemos comprobar $k_A$ es invariante bajo la elección de $h \in G_{q_0}$:
\begin{align*}
\frac{1}{\chi_M(g_q h)} (g_q \cdot h \cdot \kappa_A)(p)
=
\frac{\chi_M(h)}{\chi_M(g_q) \chi_M(h)} (g_q \cdot \kappa_A)(p)
=
\frac{1}{\chi_M(g_q)} (g_q \cdot \kappa_A)(p)
\end{align*}
El kernel $k_A$ también satisface el requisito de simetría \eqref{eq:equivariant_kernel_symmetry} del Lema del Operador Integral Equivariante:
\begin{align*}
\chi_M(g) \, k_A(g \cdot p,g \cdot q)
&=
\chi_M(g) \, \frac{1}{\chi_M(g_{(g\cdot q)})} (g_{(g\cdot q)} \cdot \kappa_A)(g \cdot p)
\\
&=
\chi_M(g) \, \frac{1}{\chi_M(g g_{q})} (g \cdot g_{q} \cdot \kappa_A)(g \cdot p)
\\
&=
\frac{\chi_M(g)}{\chi_M(g)\chi_M(g_{q})} (g_{q} \cdot \kappa_A)(g^{-1}g \cdot p)
\\
&=
\frac{1}{\chi_M(g_q)} (g_q \cdot \kappa_A)(p)
\\
&=
k_A(p,q)
\end{align*}
Por el lema anterior, tenemos que:
\begin{equation*}
\sup_{q \in N} \int_{M} |k_A(p,q)| \d p
=
\left\Vert k_A(\,\cdot\,,q_0) \right\Vert_{L^1(M)}
=
\left\Vert \kappa_A \right\Vert_{L^1(M)}
< \infty
\end{equation*}
En consecuencia, $A$ también satisface \eqref{eq:kernel_boundedness_requirement} y es un operador lineal equivariante acotado según el Lema del Operador Integral Equivariante.
$\boxed{\Leftarrow}$: Suponiendo que tenemos un operador lineal equivariante $A$ con kernel $k_A \in \operatorname{C}(M \times N)$ entonces escogemos un $q_0 \in N$ fijo y definimos $\kappa_A \in \operatorname{C}(M)$
\begin{equation*}
\kappa_A(p) := k_A(p,q_0)
\end{equation*}
Este kernel reducido $\kappa_A$ satisface la condición de compatibilidad \eqref{eq:kernel_compatibility} ya que si $h \in G_{q_0}$ entonces
\begin{align*}
(h \cdot \kappa_A)(p)
&=
k_A(h^{-1} \cdot p, q_0)
\\
&=
k_A(h^{-1} \cdot p, h^{-1} \cdot q_0)
\\
&=
\chi_M(h) \, k_A(p, q_0)
\\
&=
\chi_M(h) \, \kappa_A(p)
\end{align*}
Como requerimos $k_A(\,\cdot\,,q) \in \operatorname{L}^1(M)$ para algún $q \in N$, aplicamos el Lema anterior para encontrar
\begin{equation*}
\left\Vert \kappa_A \right\Vert_{L^1(M)}
=
\left\Vert k_A(\ \cdot\ ,q_0) \right\Vert_{L^1(M)}
=
\left\Vert k_A(\ \cdot\ ,q) \right\Vert_{L^1(M)}
<
\infty.
\end{equation*}
El Teorema de Operadores Lineales Equivariantes es el núcleo de las CNNs equivariantes, ya que nos permite generalizar la operación de convolución presente en las CNNs a operadores lineales generales que son equivariantes con respecto a un grupo de elección.
!!!side:57
Dejamos como ejercicio relacionar los dos kernels $\kappa$ y $\check{\kappa}$: ¿cuándo es $\kappa \star_G f = \check{\kappa} *_G f$?
!!!def:Correlación Cruzada y Convolución de grupos
Sea $G=M=N$ un grupo de Lie y, como ya comentamos, un grupo de Lie siempre admite una medida de Haar, por lo que tenemos un carácter trivial $\chi=1$.
Como elemento de referencia elegimos obviamente el elemento unitario $e$, aunque valdría cualquier elemento del grupo, por lo que, tanto $G_g = \{ e \}$, como $G_{e,g}=\{ g \}$, son triviales.
Cualquier $\kappa_A \in C(G) \cap L^1(G)$ define un operador lineal $A: C(G) \cap B(G) \to C(G) \cap B(G)$ mediante:
\begin{equation*}
(Af)(h)
=
\int_G (h \cdot \kappa_A)(g) \, f(g) \, \d g
=
\int_G \kappa_A (h^{-1} g) \, f(g) \, \d g
\end{equation*}
En general, llamaremos a esta operación **correlación cruzada de grupos** y la denotaremos como:
\begin{equation*}
(\kappa \star_G f)(h)
:=
\int_G (h \cdot \kappa)(g) \, f(g) \, \d g
\end{equation*}
Al igual que en el conocido escenario $\mathbb{R}^n$, la correlación cruzada de grupo está estrechamente relacionada con la **convolución de grupo**, que se define como [57]:
\begin{equation*}
(\check{\kappa} *_G f)(h)
:=
\int_G \check{\kappa} (g^{-1} h) \, f(g) \, \d g
\end{equation*}
Como en el caso $\mathbb{R}^n$, cuando hablemos de convolución de grupo nos referimos tanto a la correlación cruzada de grupo como a la convolución de grupo, ya que son intercambiables.
!!!ejemplo:Equivarianza por rotación-traslación en $\mathbb{R}^2$
Sea $G=\operatorname{SE}(2)= \mathbb{R}^2 \rtimes \operatorname{SO}(2)$ y $M=N=\mathbb{R}^2$.
La medida de Lebesgue sobre $\mathbb{R}^2$ es invariante por rotación-translación, es decir, es una integral G-invariante sobre $\mathbb{R}^2$.
Escojamos $\mathbb{y}_0=\mathbb{0}$ como elemento de referencia. En este caso, $G_{\mathbb{y}_0}=\left\{ (\mathbb{0},\, R(\theta)) \in G \ \middle\vert\ \theta \in [0,2\pi) \right\}$ es el estabilizador de $\mathbb{y}_0$.
Un kernel $\kappa_A$ en $\mathbb{R}^2$ es entonces compatible si
\begin{equation*}
(\mathbb{0},\, R(\theta)) \cdot \kappa_A = \kappa_A
\qquad
\forall \theta \in [0,2\pi)
\end{equation*}
es decir, $\kappa_A$ tiene que ser radialmente simétrica.
Realmente, este último ejemplo se podría haber deducido sin construir todo el marco de equivarianza. La siguiente sección mostrará cómo podemos utilizar el marco definido anteriormente para superar la severa restricción que se impone a los kernels permitidos aquí.
# Construcción de una CNN equivariante
¿Cómo utilizamos ahora este marco para construir una red invariante por rotación-traslación para imágenes?
Del ejemplo anterior sabemos que no tenemos mucha libertad en la formación de un operador equivariante por rotación-traslación de $\mathbb{R}^2$ a $\mathbb{R}^2$, pero podemos conseguir mucha más libertad haciendo que la primera operación lineal de nuestra red sea una que mapee funciones en $\mathbb{R}^2$ a funciones en $\operatorname{SE}(2)$. Una vez que estamos operando en el grupo tenemos mucha más libertad ya que la convolución de grupo es equivariante.
En el contexto del análisis de imágenes, el proceso de transformación de una imagen a una representación de mayor dimensión se denomina **elevación**. Por lo tanto, llamaremos a la primera capa de nuestra red **capa de elevación**.
Tras ella, y al igual que en una CNN convencional, podemos tener una serie de capas de convolución de grupo que constituyen la mayor parte de nuestra red. Como es probable que no queramos que nuestro producto final sea un elemento del grupo y puede ser interesante volver a $\mathbb{R}^2$, hemos de buscar alguna receta para ello. Puesto que pasar del espacio tridimensional $\operatorname{SE}(2)$ al espacio bidimensional $\mathbb{R}^2$ es similar a una proyección, llamaremos **capa de proyección** a la capa que hace esto.
Este diseño de tres etapas se ilustra en la figura siguiente (sobre una imagen médica de entrada):
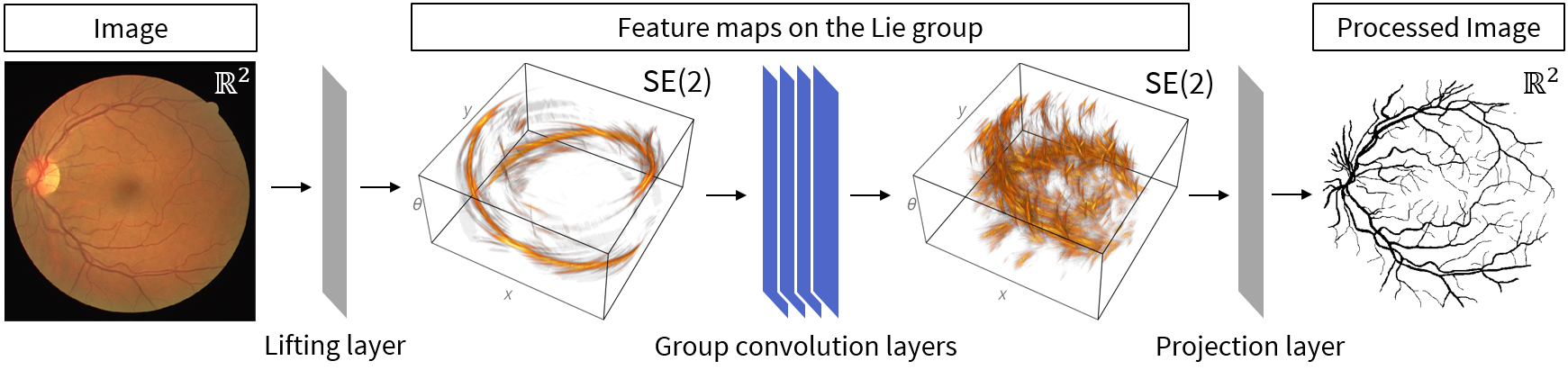
## Capa de Elevación
En las condiciones que estamos, debemos hacer uso de $G=\operatorname{SE}(2) \equiv \mathbb{R}^2 \rtimes [0, 2\pi)$ utilizando la parametrización del ejemplo de Grupo Especial Euclídeo. Sea $M=\mathbb{R}^2$ y $N=G$, y escojamos $e=(\mathbb{0},0) \in N$ como elemento de referencia, entonces el estabilizador $G_e$ es trivialmente $\{e\}$, por lo que cualquier kernel sobre $M=\mathbb{R}^2$ es compatible. Además, la medida de Lebesgue es equivariante por rotación-traslación por lo que tenemos una integral invariante.
Sea $n_0 \in \{ 1,3 \}$ el número de canales de entrada y denotemos las funciones de entrada como $f^{(0)}_{j}:\mathbb{R}^2 \to \mathbb{R}$ para $j=1,\dots,n_0$. Vamos a denotar el número de mapas de características deseadas en las primeras capas como $n_1$. Recordemos que hay dos convenciones para las capas de convolución: monocanal y multicanal.
En la configuración multicanal asociamos a cada canal de salida un número de kernels igual al número de canales de entrada. Nuestros parámetros serían un conjunto $\{ \kappa^{(1)}_{ij}\}_{ij} \subset C(\mathbb{R}^2) \cap L^1(\mathbb{R}^2)$ de núcleos y un conjunto $\{ b^{(1)}_i \}_{i} \subset \mathbb{R}$ de sesgos para $i=1,\dots,n_1$ y $j=1,\dots, n_0$. El cálculo para el canal de salida $i$ viene dado entonces por:
\begin{equation*}
f^{(1)}_{i}(\mathbb{x},\theta)
=
\sigma \left(
\sum_{j=1}^{n_0}
\int_{\mathbb{R}^2} \left( (\mathbb{x},\theta) \cdot \kappa^{(1)}_{ij}\right) (\mathbb{y}) \, f^{(0)}_{j}(\mathbb{y}) \, \d \mathbb{y} + b^{(1)}_{i}
\right)
\end{equation*}
para alguna elección de la función de activación $\sigma$.
En la configuración monocanal, asociamos un núcleo a cada canal de entrada y, a continuación, realizamos combinaciones lineales de los canales de entrada convolucionados para generar canales de salida. Nuestros parámetros consistirían entonces en un conjunto de kernels $\{ \kappa^{(1)}_{j} \}_{j} \subset C(\mathbb{R}^2) \cap L^1(\mathbb{R}^2)$ y un conjunto de pesos $\{ a^{(1)}_{ij} \}_{ij} \subset \mathbb{R}$ y sesgos $\{ b^{(1)}_i \}_{i} \subset \mathbb{R}$ para $i= 1,\dots,n_1$ y $j=1,\dots,n_0$. El cálculo para el canal de salida $i$ viene dado entonces por
\begin{equation*}
f^{(1)}_{i}(\mathbb{x},\theta)
=
\sigma \left(
\sum_{j=1}^{n_0}
a^{(1)}_{ij}
\int_{\mathbb{R}^2}
\left( (\mathbb{x},\theta) \cdot \kappa^{(1)}_{j} \right)(\mathbb{y})
\, f^{(0)}_{j}(\mathbb{y}) \, \d\mathbb{y}
+ b^{(1)}_{i}
\right)
\end{equation*}
En cualquier caso, la elevación real ocurre mediante la traslación y rotación del kernel sobre la imagen, una traslación y rotación particular nos da un valor escalar particular en la ubicación correspondiente a $\operatorname{SE}(2)$.
## Capa de convolución de grupo
En la sección anterior vimos cómo hace convoluciones de un grupo en sí mismo. En el grupo de Lie siempre tenemos una integral invariante (la integral de Haar izquierda) y el requisito de simetría en el kernel es trivial, por lo que no tenemos restricciones a tener en cuenta para el entrenamiento del kernel (a diferencia del caso $\mathbb{R}^2 \to \mathbb{R}^2$).
En la capa $\ell \in \mathbb{N}$ con $n_{\ell-1}$ canales de entrada y $n_{\ell}$ canales de salida el cálculo para el canal de salida $i$ viene dado (para la configuración monocanal) por:
\begin{equation*}
f^{(\ell)}_{i}
=
\sigma \left(
\sum_{j=1}^{n_{\ell-1}}
a^{(\ell)}_{ij}
\left(
\kappa^{(\ell)}_{j}
\star_G
f^{(\ell-1)}_{j}
\right)
+
b^{(\ell)}_{i}
\right)
\end{equation*}
para cada $i \in \{1, \ldots, n_{\ell} \}$ o
\begin{equation*}
f^{(\ell)}_{i} (\mathbb{x},\theta)
=
\sigma \left(
\sum_{j=1}^{n_{\ell}}
a^{(\ell)}_{ij}
\int_{\mathbb{R}^2}
\int_{0}^{2\pi}
\left( (\mathbb{x},\theta) \cdot \kappa^{(\ell)}_{j} \right)
(\mathbb{y},\alpha)
\
f^{(\ell-1)}_{j}(\mathbb{y},\alpha)
\
\d\alpha \d\mathbb{y}
+
b^{(\ell)}_{i}
\right)
\end{equation*}
!!!side:58
La deducción de la fórmula para la configuración multicanal la dejamos como ejercicio.
para alguna elección de la función de activación $\sigma$. Aquí los núcleos $\kappa^{(\ell)}_{j} \in C(G)\times L^1(G)$, los pesos $a^{(\ell)}_{i j} \in \mathbb{R}$ y los sesgos $b^{(\ell)}_i \in \mathbb{R}$ son los parámetros entrenables [58].
Las capas de convolución de grupo se pueden apilar secuencialmente igual que las capas de convolución normales en una CNN para formar el corazón de una G-CNN, como muestra la figura anterior.
## Proyección
Como hemos comentado, es probable que la salida deseada de nuestra red no sea un mapa de características sobre el grupo o algún otro espacio homogéneo de mayor dimensión, y en ese caso tenemos que proyectar en algún otro espacio de interés.
En las CNN tradicionales utilizadas para la clasificación es común aplanar la matriz multidimensional *olvidando* las dimensiones espaciales. Una vez que hemos discretizado, el aplanamiento es, por supuesto, un enfoque viable para una G-CNN cuando el objetivo es la clasificación, pero es posible que no queramos perder la estructura espacial y se necesite volver al espacio de entrada original (como en el ejemplo mostrado en la figura).
Aplicando el marco de equivarianza de nuevo al caso $G=M=\operatorname{SE}(2)$ y $N=\mathbb{R}^2$. Elegimos $\mathbb{0} \in N$ como elemento de referencia, por lo que su estabilizador es el subgrupo formado solo por las rotaciones. Así que para construir un operador lineal equivariante de $\operatorname{SE}(2)$ a $\mathbb{R}^2$ se requiere un núcleo $\kappa$ en $\operatorname{SE}(2)$ que satisfaga
\begin{equation*}
(\mathbb{0},\, \beta) \cdot \kappa = \kappa
\quad\Leftrightarrow\quad
\kappa(\mathbb{x},\,\theta)
=
\kappa\left( R(-\beta) \mathbb{x},\, \theta - \beta \right)
\qquad
\forall \beta,\theta \in [0,2\pi),\, \mathbb{x} \in \mathbb{R}^2
\end{equation*}
donde $R(-\theta)$ es la matriz de rotación de ángulo $-\theta$.
Concesuentemente, pordemos reducir la parte (no restringida) entrenable del kernel $\kappa$ a un corte 2D:
\begin{equation*}
\kappa(\mathbb{x},\theta)
=
\kappa\left( R(-\theta)\mathbb{x},\, 0 \right)
\end{equation*}
Un núcleo como este nos da el operador lineal equivariante deseado, y con varios de estos núcleos podemos construir una capa de la misma manera en que hemos hecho con la capa de elevación y convolución de grupo.
En la práctica, este tipo de operador con kernel entrenable no es el que se utiliza para la proyección desde $\operatorname{SE}(2)$ a $\mathbb{R}^2$. En su lugar se utiliza la integración, mucho más simple (y no entrenable), sobre el eje $\theta$: sea $f \in \operatorname{B}(\operatorname{SE}(2))$, entonces el operador $P:C(\operatorname{SE}(2)) \cap B(\operatorname{SE}(2)) \to C(\mathbb{R}^2) \cap B(\mathbb{R}^2)$ dado por:
\begin{equation}
\label{eq:integration_over_theta}
(Pf)(\mathbb{x})
:=
\int_{0}^{2\pi} f(\mathbb{x},\theta) \, \d\theta
\end{equation}
es un operador lineal acotado que es equivariante por rotación-traslación.
!!!note
Obsérvese que el operador de proyección \eqref{eq:integration_over_theta} es uno de nuestros operadores lineales equivariantes si tomamos el núcleo como $\kappa_P(\mathbb{x},\theta)=\delta(\mathbb{x})$ donde $\delta$ es la delta de Dirac en $\mathbb{R}^2$. La delta de Dirac no es una función en $C(G) \cap L^1(G)$ pero podemos tomar una sucesión en $C(G) \cap L^1(G)$ que converja débilmente a $\kappa_P$, por ejemplo, una sucesión de gaussianas cada vez más estrechas.
Una alternativa común a la integración sobre el eje de orientación es tomar el máximo sobre ese eje:
\begin{equation}
\label{eq:max_projection_layer}
\left( P_{\max} f \right)(\mathbb{x})
:=
\max_{\theta \in [0,2\pi)}
\,
f(\mathbb{x},\theta)
\end{equation}
que no es un operador lineal, pero es equivariante por rotación-traslación, volveremos sobre este operador de proyección más adelante.
Después de haber obtenido una vez más mapas de características en $\mathbb{R}^2$ podemos proceder a nuestro formato de salida deseado de la misma manera que lo haríamos con una CNN clásica: o bien nos olvidamos de las dimensiones espaciales y pasamos a una red totalmente conectada para aplicaciones de clasificación, o bien tomamos una combinación lineal de los mapas de características 2D obtenidos para generar una imagen de salida.
## Discretización
Para aplicar en la práctica la G-CNN que se han desarrollado hay que pasar a una configuración discretizada. Para el caso específico de una G-CNN en $\operatorname{SE}(2)$, la capa de elevación suele utilizar núcleos de tamaño $5 \times 5$ a $$7 \times 7$, y es común tomar $8$ orientaciones discretas, por lo que una entrada de $\mathbb{R}^{H \times W}$ se elevaría a $\mathbb{R}^{8\times H \times W}$. Puede parecer poco, pero empíricamente es el punto óptimo entre rendimiento y uso de memoria/tiempo de cálculo. Las capas de convolución de grupo suelen emplear $5 \times 5 \times 5$ kernels. En cualquier caso, es necesario muestrear el kernel fuera de la red para poder rotarlos, para lo que se suele usar interpolación lineal.
!!!ejemplo
Una CNN tradicional (izquierda) frente a una G-CNN equivariante por rotación-traslación (derecha) para segmentar una imagen en color con un tamaño de $h \times w$:

!!!ejemplo
Una CNN tradicional (izquierda) frente a una G-CNN equivariante por rotación-traslación (derecha) para clasificar imágenes $28 \times 28$ en escala de grises en $10$ clases. La clasificación de dígitos entra dentro de esta categoría.

Como regla general, en el aprendizaje profundo discretizamos lo más toscamente posible. Aumentar el tamaño de los núcleos o el número de orientaciones aumenta el rendimiento, pero no es ni mucho menos proporcional al aumento de memoria y tiempo de cálculo que esto provoca, así que mantener los núcleos grandes y aumentar la profundidad de la red es una mejor manera de gastar un presupuesto dado de memoria y tiempo.
!!!note:Alternativas de interpolación lineal
Los métodos de interpolación polinómica de orden superior son altamente indeseables en mallas tan toscas, ya que las oscilaciones pueden hacer que la red se comporte de forma errática. Se han propuesto técnicas de interpolación más avanzadas, por ejemplo por B-splines [#bekkers2021], pero la complejidad computacional añadida puede ser un inconveniente. Al igual que con la discretización, la regla de oro para la interpolación es: tan toscamente como aguante.
# Bibliografía
[#bekkers2021]: Bekkers, Erik J (2021). B-Spline CNNs on Lie Groups. arXiv: 1909.12057 [cs.LG].
[#cohen2016]: Cohen, Taco and Max Welling (2016). “Group Equivariant Convolutional Networks”. In: International Conference on Machine Learning. PMLR, pp. 2990–2999.
[#cohen2020]: Cohen, Taco, Mario Geiger, and Maurice Weiler (2020). A General Theory of Equivariant CNNs on Homogeneous Spaces. arXiv: 1811.02017 [cs.LG].
[#duchi2011]: Duchi, John, Elad Hazan, and Yoram Singer (2011). “Adaptive subgradient methods for online learning and stochastic optimization.” In: Journal of Machine Learning Research 12.7.
[#federer2014]: Federer, Herbert (2014). Geometric Measure Theory. Springer. isbn: 978-3-540-60656-7. doi: 10.1007/978-3-642-62010-2.
[#fukushima1987]: Fukushima, Kunihiko (1987). “Neural network model for selective attention in visual pattern recognition and associative recall”. Applied Optics 26.23, pp. 4985–4992.
[#glorot2010]: Glorot, Xavier; Yoshua Bengio (2010). “[Understanding the difficulty of training deep feed forward neural networks](https://proceedings.mlr.press/v9/glorot10a.html)”. Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics. Ed. by Yee Whye Teh and Mike Titterington. Vol.9. Proceedings of Machine Learning Research. Chia Laguna Resort, Sardinia, Italy: PMLR, pp. 249–256.
[#golan1999]: Golan, Jonathan S. (1999). Semirings and their Applications. Dordrecht: Springer Netherlands. isbn: 978-90-481-5252-0. doi: 10.1007/78-94-015-9333-5. url: http://link.springer.com/10.1007/978-94-015-9333-5.
[#he2015]: He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun (2015). Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. arXiv: 1502.01852 [cs.CV].
[#ivakhnenko1966]: Ivakhnenko, Aleksei Grigorevich; Valentin Grigorevich Lapa (1966). Cybernetic predicting devices. Tech. rep. Purdue Univ Lafayette Ind School of Electrical Engineering.
[#kingma2017]: Kingma, Diederik P. and Jimmy Ba (2017). Adam: A Method for Stochastic Optimization. arXiv: 1412.6980 [cs.LG].
[#kolokoltsov1997]: Kolokoltsov, Vassili N. and Victor P. Maslov (1997). Idempotent Analysis and Its Applications. Dordrecht: Springer Netherlands. isbn: 978-90-481-4834-9. doi: 10.1007/978-94-015-8901-7. url: http://link.springer.com/10.1007/978-94-015-8901-7.
[#krizhevsky2012]: Krizhevsky, Alex, Ilya Sutskever, Geoffrey E Hinton (2012). “[ImageNet Classification with Deep Convolutional Neural Networks](https://proceedings.neurips.cc/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf)”. Advances in Neural Information Processing Systems. Ed. by F. Pereira, C.J. Burges, L. Bottou, and K.Q. Weinberger. Vol. 25. Curran Associates, Inc.
[#lecun1998]: LeCun, Yann; Léon Bottou; Yoshua Bengio; Patrick Haffner (1998). “Gradient-based learning applied to document recognition”. In: Proceedings of the IEEE 86.11, pp. 2278–2324.
[#lecun1989]: LeCun, Yann; Bernhard Boser, John S Denker, Donnie Henderson, Richard E Howard, Wayne Hubbard, Lawrence D Jackel (1989).“Backpropagation applied to handwritten zipcode recognition”. Neural computation 1.4, pp. 541–551.
[#lee2010]: Lee, John M. (2010). Introduction to Topological Manifolds. 2nd ed. Graduate Texts in Mathematics. Springer. isbn: 978-1-4419-7939-1. doi: 10.1007/978-1-4419-7940-7.
[#lee2013]: Lee, John M. (2013). Introduction to Smooth Manifolds. 2nd ed. Graduate Texts in Mathematics. Springer. isbn: 978-1-4419-9981-8. doi: 10.1007/978-1-4419-9982-5_1.
[#mcculloch1943]: McCulloch, Warren S; Walter Pitts (1943). “A logical calculus of the ideas immanent in nervous activity”. The bulletin of mathematical biophysics 5.4, pp. 115–133.
[#oh2004]: Oh, Kyoung-Su; Keechul Jung (2004). “GPU implementation of neural networks”. Pattern Recognition 37.6, pp. 1311–1314.
[#tao2011]: Tao, Terence (2011). An Introduction to Measure Theory. Vol. 126. Graduate Studies in Mathematics. American Mathematical Society. isbn: 978-1-4704-6640-4. doi: 10.1090/gsm/126.
[#tieleman2012]: Tieleman, Tijmen, Geoffrey Hinton, et al. (2012). “Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude”. In: Coursera: Neural networks for machine learning 4.2, pp. 26–31.
(insert ../menu.md.html here)