**Fundamentos** # Aprendizaje Supervisado !!!side:3 Podemos encontrar, además, el Aprendizaje No Supervisado, el Semisupervisado, Aprendizaje por Refuerzo, etc. Aunque existen diferentes tipos de aprendizaje automático, nos centraremos en esta entrada en el **Aprendizaje Supervisado** [3], un paradigma de aprendizaje automático en el que los datos disponibles están formados por pares de entradas con salidas conocidas y correctas. Se desconoce cómo funciona exactamente la correspondencia entre esas entradas y salidas, así que el objetivo que se persigue es deducir, a partir de los datos disponibles, el patrón general que sigue esta correspondencia con la esperanza de que se generalice a situaciones no vistas (es decir, que si obtenemos nuevas entradas del fenómeno estudiado, las salidas generadas por el patrón aprendido se correspondan con las salidas reales). Por tanto, formalmente, podemos plantear el problema de la siguiente manera: !!!def: El Problema del Aprendizaje Supervisado Dada una función desconocida $f:X \to Y$ entre los espacios $X$ y $Y$, encontrar una buena aproximación de $f$ utilizando sólo un conjunto de datos de muestras: \begin{equation*} \mathcal{D} = \big\{ \left( x_i, y_i \right) \big\}_{i=1}^N \quad\text{ con }\quad y_i = f(x_i) \quad\text{para todo } i=1, \ldots, N \end{equation*} El espacio $X$ se suele denominar **espacio de características**, y a sus elementos, **vectores de características**. A $Y$ se le suele denominar **espacio de etiquetas**, y a sus elementos, **etiquetas**. !!!ejemplo:Ejemplo Sea $X$ el espacio de todas las imágenes de gatos y perros y $f$ el clasificador que mapea estas imágenes al conjunto $Y=\left\{ \text{"perro"}, \text{"gato"} \right\}$. Esta tarea la podemos expresar numéricamente tomando: * $X = [0,1]^{3 \times h \times w}$, es decir, una imagen de $h$ pixels de altura, $w$ pixels de anchura $w$, y 3 canales de color. * $Y=[0,1]^2$, que determina una probabilidad de pertenencia para cada una de las dos clases consideradas. !!!side:4 La elección del símbolo $W$ viene del nombre *pesos* en inglés, ya que así es como se suele denominar a los parámetros en las redes neuronales. !!!att:Planteamiento del Problema El planteamiento general para resolver este problema plantea 3 subtareas fundamentales: 1. El conjunto de posibles aproximaciones se restringe a una familia que se conoce como **Espacio de Hipótesis**, $\cal{H}$. Como este espacio suele ser de dimensión infinita y poco estructurado, habitualmente se elige un modelo $F:X \times W \to Y$ parametrizado por un **Espacio de Parámetros**, $W$ [4], por lo que el problema se transforma de una búsqueda en $\cal{H}$ en una búsqueda en $W$. 2. Necesitamos cuantificar la *calidad* de la salida del modelo, y lo haremos por medio de una **función de pérdida** $\ell: Y \times Y \to \mathbb{R}$, donde $\ell(y_1,y_2)$ indica *cuán diferentes* son $y_1$ e $y_2$. 3. Gracias a $\ell$, la búsqueda se transforma en un proceso de optimización: haciendo uso de $\mathcal{D}$ y $\ell$, elegir $w \in W$ de modo que $F(\ \cdot\ ; w)$ sea la *mejor* aproximación posible de la función objetivo $f$. !!!note:Sesgo Inductivo Obsérvese que hemos convertido un problema de búsqueda en un problema de optimización (algo habitual en Inteligencia Artificial). Sin embargo, este enfoque de alto nivel deja algunas cuestiones abiertas: 1. ¿Cómo elegir $\mathcal{H}$? 2. ¿Cómo elegir $\ell$? 3. ¿Cómo optimizar? Ninguna de estas preguntas tiene respuestas canónicas y se manejan en gran medida por ensayo y error (*heurísticamente*), simplemente porque tenemos que fijarlos antes de que podamos hacer ningún progreso en el problema. En cualquier caso, estas elecciones tienen un gran impacto en el resultado final aunque no estén respaldadas en absoluto por los datos disponibles o por algún tipo de *primer principio* que nos ayude en la decisión. El conjunto colectivo de suposiciones que hacemos para poder proceder con el problema se denomina **sesgo inductivo** en el campo del aprendizaje automático. En nuestro caso, nuestro objetivo nos fija en gran medida el tipo de modelo que usaremos en el aprendizaje, nuestras hipótesis: las redes neuronales. En la siguiente sección haremos una presentación de este modelo con algún detalle. Con respecto a la función de pérdida, debemos tener en cuenta que ésta funciona como una métrica, pero es menos restrictiva: * Por lo general, pero no siempre, $\ell: Y \times Y \to \mathbb{R}^+$. * Como queremos minimizar la pérdida, el mínimo debe existir: $\forall y_0\in Y\ (\displaystyle{min_{y \in Y} \ell(y_0,y)} \in Y)$. * Sería interesante que fuera diferenciable (en casi todo, por lo menos), para así poder usar el descenso por gradiente como método de optimización. !!!side:5 Identidad de indiscernibles: $\ell(y_1,y_2)=0 \Rightarrow y_1=y_2$.
Simetría: $\ell(y_1,y_2)=\ell(y_2,y_1)$.
Desigualdad triangular: $\ell(y_1,y_2)\leq \ell(y_1,y_3)+\ell(y_3,y_2)$. * No es necesario que se cumplan propiedades métricas como identidad de indiscernibles, simetría y desigualdad triangular [5]. Una vez elegidos un modelo y una función de pérdida, pasamos a la optimización, es decir: ¿cuál es la *mejor* elección de $w \in W$? La respuesta directa (aunque no necesariamente la preferida) es *minimizar la pérdida en el conjunto de datos*, es decir, encontrar: \begin{equation*} w^* = \operatorname{arg\,min}_{w \in W} \sum_{i=1}^N \ell \left( F(\, x_i\,;w), y_i \right) \end{equation*} !!!ejemplo:Mínimos cuadrados lineales Si partimos de una familia de funciones base: $\Theta=\{ \varphi_j \}_{j=1}^n$, podemos considerar la familia de hipótesis lineales respecto a $\Theta$ como: \begin{equation*} F(x;w) = \sum_{j=1}^n w_j \varphi_j(x) \end{equation*} donde $w=(w_1,\dots,w_n)\in \mathbb{R}^n$. Si, además, definimos $\ell(y_1,y_2)=| y_1 - y_2 |^2$, obtenemos la configuración habitual de mínimos cuadrados lineales. El *mejor* $w\in W$ no es necesariamente el que minimiza la pérdida en el conjunto de datos, el **sobreajuste** es a menudo un problema en cualquier problema de optimización: podría ocurrir que el $w\in W$ que minimiza el conjunto de datos no generaliza bien cuando comenzamos a usar la aproximación fuera de los datos conocidos. !!!side:6 Por ejemplo, no permitir valores de $w$ demasiado grandes. Para mitigar este efecto podemos introducir el concepto de **regularización**. Aunque discutiremos las técnicas de regularización más adelante, por ahora mencionaremos que la regularización de parámetros es una técnica común que se utiliza a menudo en las redes neuronales. Este tipo específico de regularización se caracteriza por la adición de un término de penalización a la pérdida de datos que perjudica los valores de los parámetros que se encuentran en áreas no deseadas [6]. El problema de optimización modificado pasa a ser: \begin{equation*} w^* = \operatorname{arg\,min}_{w \in W} \left( \sum_{i=1}^N \ell \left( F(x_i;w), y_i \right) + \lambda C(w) \right) \end{equation*} con $\lambda>0$ y $C:W \to \mathbb{R}^+$ una función de coste que penalizar de algún modo la complejidad de los parámetros. !!!ejemplo:Regularización de Tikhonov En el caso particular en que tenemos $W=\mathbb{R}^n$ y tomamos como penalización $C(w) = \| w \|^2$, obtenemos la conocida como **Regularización de Tikhonov**, también conocida en el contexto de las redes neuronales como **Decaimiento de Pesos**. En este caso, se penalizan los pesos que tienen un tamaño excesivo. ## Regresión y Clasificación El aprendizaje supervisado no es un concepto extraño en matemáticas, de hecho: !!!def:Regresión Si $X=\mathbb{R}^n$ y $Y=\mathbb{R}^m$ entonces el aprendizaje supervisado equivale a **regresión**. Aunque la regresión es una gran parte del aprendizaje supervisado, la formulación de éste se hace más general para que abarque otras tareas como la *clasificación*: !!!def:Clasificación La clasificación es la designación ML para la regresión logística (multiclase) donde $X=\mathbb{R}^n$ e intentamos asignar cada $x \in X$ a una de las $m$ clases posibles. La salida numérica para este tipo de problema es normalmente una distribución de probabilidad discreta sobre $m$ clases: \begin{equation*} Y = \left\{ (y_1,\ldots,y_m) \in [0,1]^m \ \middle| \ \textstyle\sum_{i=1}^m y_i = 1 \right\}. \end{equation*} El ejemplo de perros y gatos apuntado anteriormente es de este tipo. La aproximación más común cuando se presenta una teoría robusta que permita enmarcar el Aprendizaje Automático es aplicando conceptos de Estadística, lo que daría lugar a: !!!note:Teoría estadística del aprendizaje (SLT) En SLT se supone que las muestras de datos $(x_i,y_i)$ se extraen i.i.d. de alguna distribución de probabilidad $\mu$ en $X \times Y$. En este caso, lo que interesa minimizar es el conocido como **riesgo poblacional**: \begin{equation*} R(w) := \mathbb{E}_{(x,y) \sim \mu} \left[ \ell\left( F(x;w), y \right) \right] := \int_{X \times Y} \ell\left( F(x;w), y \right) \d\mu(x,y) \end{equation*} El objetivo sería encontrar el conjunto de parámetros que minimiza este riesgo poblacional: \begin{equation*} w^* = \operatorname{arg\,min}_{w \in W} R(w) \end{equation*} Pero en realidad no conocemos $\mu$ y, por tanto, ni siquiera podemos calcular el riesgo poblacional, y mucho menos minimizarlo. Así que hacemos lo mejor que podemos hacer con lo que tenemos en las manos, minimizar el **riesgo empírico**: \begin{equation*} \hat{R}(w) := \frac{1}{N} \sum_{i=1}^N \ell\left( F(x_i;w), y_i \right) \end{equation*} El conjunto de parámetros que minimiza el riesgo empírico se denomina **minimizador empírico**: \begin{equation*} \hat{w} = \operatorname{arg\,min}_{w \in W} \hat{R}(w), \end{equation*} que es lo mismo que minimizar la pérdida en el conjunto de datos en el marco del aprendizaje supervisado. Cuando añadimos un término de regularización se denomina **minimización del riesgo estructural**: \begin{equation*} \hat{w} = \operatorname{arg\,min}_{w \in W} \hat{R}(w) + \lambda C(w). \end{equation*} SLT se ocupa, entonces, de estudiar cosas tales como límites en $\hat{R}(\hat{w})-R(w^*)$. A pesar de ello, aquí nos separamos un poco de esta aproximación, en primer lugar por gusto personal, y en segundo lugar porque necesitaremos una estructura más rica para poder extraer una comprensión mayor del caso del Aprendizaje Profundo. # Neuronas Artificiales  Como su nombre indica, las redes neuronales artificiales se inspiran en la biología. En la imagen adyacente se representa una neurona biológica simplificada. Las dendritas de la izquierda reciben señales eléctricas de otras neuronas, una vez alcanzado un determinado umbral la neurona disparará una señal a lo largo de su axón y, a través de sus sinapsis de la derecha, retransmitirá una señal a otras neuronas. Cada neurona puede enviar y recibir señales hacia y desde otras neuronas, de modo que el entramado de diversas neuronas interconectadas forman lo que denomina una **red neuronal**. De forma similar, las redes neuronales artificiales están formadas por neuronas artificiales. Cada neurona artificial toma algunas entradas (normalmente en forma de números reales) y produce una o más salidas (de nuevo, normalmente números reales) que pasa a otras neuronas. El modelo de neurona más común viene dado por una transformada afín seguida de una función no lineal.  !!!def:Neurona Artificial Sea $\mathbb{x} \in \mathbb{R}^n$ la señal de entrada e $\mathbb{y} \in \mathbb{R}^m$ la señal de salida, entonces calculamos \begin{equation} \label{eq:affineneuron} \mathbb{y} = \varphi ( A \mathbb{x} + \mathbb{b}), \end{equation} donde $A \in \mathbb{R}^{m \times n}$, $\mathbb{b} \in \mathbb{R}^m$ y $\varphi$ es una elección de **función de activación**. Los componentes de la matriz $A$ se denominan **pesos lineales**, el vector $\mathbb{b}$ se denomina **sesgos**. El valor intermedio $A \mathbb{x} + \mathbb{b}$ a veces se denomina **activación**. La función de activación $\varphi$ también se denomina a veces **función de transferencia o de no linealidad**. Las entradas y salidas no tienen por qué restringirse a números reales. Dependiendo de la aplicación, podríamos encontrarnos: * $\{0, 1\}$: binario, * $\mathbb{R}^+$: reales no negativos, * $[0,1]$: intervalos (probabilidades, por ejemplo), * $\mathbb{C}$: complejos, * etc. !!!def:Perceptrones Una elección históricamente significativa de la función de activación es la función **Heaviside**, dada por \begin{equation*} H(x) := \mathbb{1}_{x \geq 0}(x) := \begin{cases} 1 \qquad &\text{si } x \geq 0, \\ 0 &\text{en otro caso} \end{cases} \end{equation*} Una neurona del tipo anterior que utiliza la función Heaviside como función de activación se denomina **perceptrón**. Veamos lo que podemos hacer con él: Sea $\mathbb{w} \in \mathbb{R}^n$ y $b \in \mathbb{R}$ entonces una neurona con entrada $\mathbb{x} \in \mathbb{R}^n$ y salida $y \in \mathbb{R}$ sería como \begin{equation*} \mathcal{N}(\mathbb{x}) = H(\mathbb{w}^T \mathbb{x} + b) = \begin{cases} 1 \qquad &\text{si } \mathbb{w}^T \mathbb{x} \geq -b, \\ 0 &\text{si } \mathbb{w}^T \mathbb{x} < -b \end{cases} \end{equation*} Que no es más que un clasificador binario lineal en $\mathbb{R}^n$ ya que $\mathbb{w}^T \mathbb{x} = -b$ es un hiperplano en $\mathbb{R}^n$. Este hiperplano divide el espacio en dos y asigna el valor $0$ a una mitad y $1$ a la otra. !!!ejemplo:Puerta Booleana Podemos (entre otras cosas) utilizar un perceptrón para modelar algo de lógica booleana elemental. Sean $x_1,x_2 \in \{0,1\}$ y sea $\operatorname{AND}(x_1,x_2) := H(x_1+x_2-1,5)$ entonces la neurona se comporta como la función booleana de la conjunción: \begin{array}{ccc} x_1 & x_2 & \operatorname{AND}(x_1,x_2) \\ \hline 0 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \end{array} La función Heaviside es un ejemplo de una función de activación escalar. A menudo, cuando se utiliza una función escalar como función de activación abusamos de la notación para que acepte vectores (y matrices) en lo que denominamos aplicación punto a punto: !!!note:Notación Sea $\varphi: \mathbb{R} \to \mathbb{R}$ entonces extendemos $\varphi: \mathbb{R}^n \to \mathbb{R}^n$ como: \begin{equation*} \varphi \left( \begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix} \right) \equiv \begin{bmatrix} \varphi(x_1) \\ \vdots \\ \varphi(x_n) \end{bmatrix} \end{equation*} Enumeramos algunas funciones de activación escalar de uso común que también (se ilustran en la figura siguiente y a continuación se dan las definiciones funcionales):  * *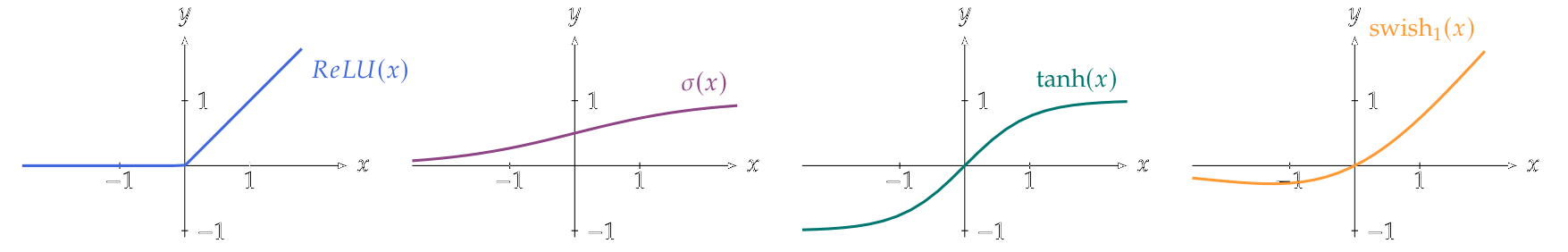Rectified Linear Unit* (ReLU): posiblemente la función de activación más utilizada en las redes neuronales modernas, se calcula como: \begin{equation*} \operatorname{ReLU}(\lambda) := \max\{0, \lambda \} \end{equation*} * *Sigmoidea* (también conocida como sigmoide logística o, simplemente, sigmoide): \begin{equation*} \sigma(\lambda) := \frac{1}{1 + e^{-\lambda}} \end{equation*} La sigmoidea se utilizó comúnmente como función de activación en las primeras redes neuronales, que es la razón por la que las funciones de activación en general todavía se nombran a menudo con $\sigma$. * *Tangente Hiperbólica*: muy similar a la sigmoidea, viene dada por: \begin{equation*} \tanh(\lambda) := \frac{e^\lambda - e^{-\lambda}}{e^{\lambda}+e^{-\lambda}} \end{equation*} !!!side:7 El parámetro $\beta$ se elige normalmente como $1$ pero podría ser tratado como un parámetro entrenable si se desea. En este caso también se denomina *unidad lineal ponderada sigmoidea* o SiLU. * *Swish*: una elección más reciente de la función de activación que puede considerarse como una variante suave de la ReLU. Viene dada por la multiplicación de la propia entrada por la función sigmoidea: \begin{equation*} \operatorname{swish_\beta}(\lambda) := \lambda \, \sigma(\beta\lambda) := \frac{\lambda}{1 + e^{-\beta \lambda}} \end{equation*} donde $\beta > 0$ [7]. 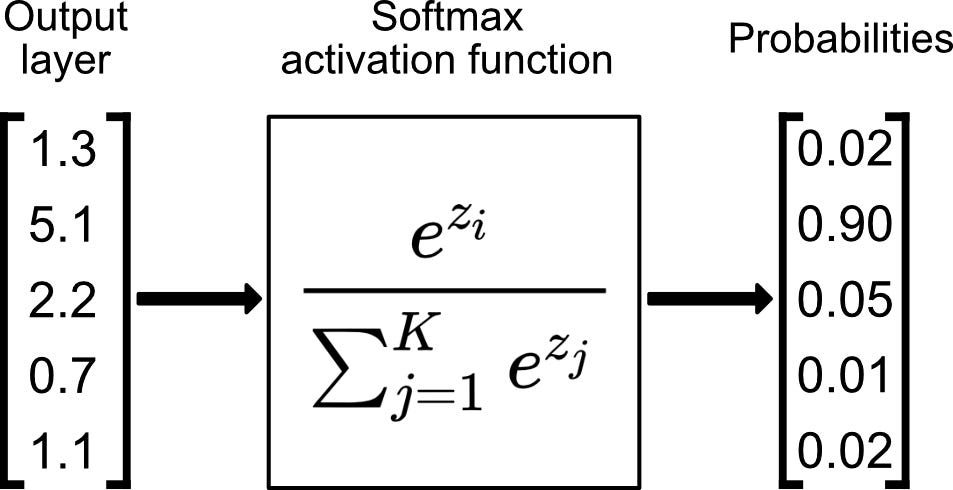Pero también son habituales funciones de activación no escalares, enumeramos algunas funciones multivariantes comunes: !!!side  * *Softmax*, también conocida como función exponencial normalizada: $\text{softmax}:\mathbb{R}^n \to [0,1]^n$ dada por: \begin{equation*} \operatorname{softmax} \left( \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \right) := \frac{1}{\sum_{i=1}^n e^{x_i}} \begin{bmatrix} e^{x_1} \\ e^{x_2} \\ \vdots \\ e^{x_n} \end{bmatrix} \end{equation*} $\operatorname{softmax}$ tiene el objetivo de poder interpretar su salida como una distribución de probabilidad discreta, es decir, cada valor es un real no negativo en el rango $[0,1]$, y todos los valores de su salida suman exactamente $1$. * *Maxpool*: cada salida es el máximo de un determinado subconjunto de las entradas: $\operatorname{maxpool}:\mathbb{R}^n \to \mathbb{R}^m$ dada por: \begin{equation*} \operatorname{maxpool} \left( \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \right) := \begin{bmatrix} \max_{j \in I_1} x_j \\ \max_{j \in I_2} x_j \\ \vdots \\ \max_{j \in I_m} x_j \end{bmatrix} \end{equation*} Donde para cada $i \in \{ 1,\ldots,m \}$ tenemos un $I_i \subset \{1,\ldots,n \}$ que especifica sobre qué entradas tomar el máximo para cada salida. (esta función se puede generalizarse fácilmente sustituyendo la operación $\operatorname{max}$ por $\operatorname{min}$, media, etc.) * *Normalización*, a veces es conveniente volver a centrar y reescalar una señal: \begin{equation*} \operatorname{normalize} \left( \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \right) := \begin{bmatrix} \frac{x_1 - \mu}{\sigma} \\[5pt] \frac{x_2 - \mu}{\sigma} \\ \vdots \\ \frac{x_n - \mu}{\sigma} \end{bmatrix} \end{equation*} donde $\mu = \mathbb{E}[\mathbb{x}]$ y $\sigma^2 = \operatorname{Var}(\mathbb{x})$. Hay muchas variantes de normalización en las que la diferencia es cómo se calculan $\mu$ y $\sigma$ (en el tiempo, en subconjuntos de las señales entrantes, etc.). 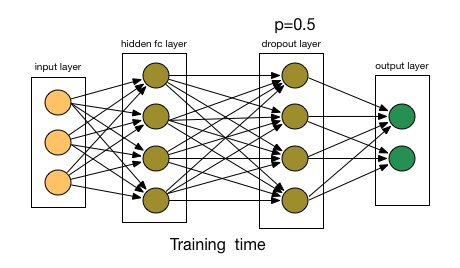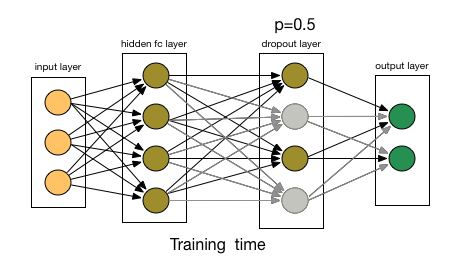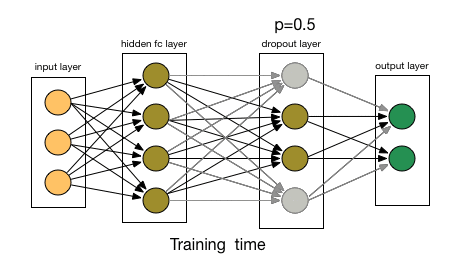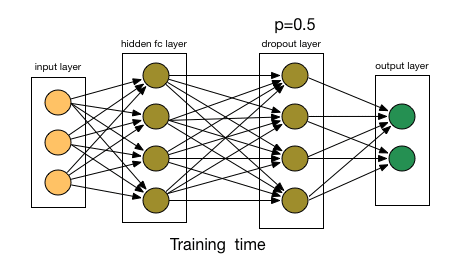Todos los ejemplos anteriores de funciones de activación (sean escalares o no) son deterministas, pero también se utilizan funciones de activación *estocásticas*: !!!side  * $\operatorname{dropout}$ es una función estocástica que se suele utilizar durante el proceso de entrenamiento, pero que se elimina una vez finalizado éste. Funciona poniendo a cero aleatoriamente valores individuales de una señal con probabilidad $p$: \begin{equation*} \left(\operatorname{dropout}_p(\mathbb{x})\right)_i := \begin{cases} 0 \qquad &\text{con probabilidad } p, \\ x_i &\text{con probabilidad } 1-p \end{cases} \end{equation*} * $\operatorname{heatbath}$ es una función escalar que da como resultado $1$ o $-1$ con una probabilidad que depende de la entrada: \begin{equation*} \operatorname{heatbath}(x) := \begin{cases} \hphantom{-}1 \qquad &\text{con probabilidad } \frac{1}{1+e^{-x}} \\ -1 \qquad &\text{en otro caso} \end{cases} \end{equation*} Todas las funciones de activación que hemos visto son esencialmente funciones fijas, $\operatorname{swish}$ y $\operatorname{dropout}$ tienen un parámetro pero suele estar prefijado a algún valor elegido durante todo el funcionamiento de la neurona. Esto significa que los parámetros entrenables de una red neuronal suelen ser los pesos lineales y los sesgos, pero no los parámetros de la función de activación. Aunque sería posible que se estos parámetros también se consideraran entrenables, tener parámetros en la parte no lineal de una red es algo raro en la práctica actualmente. # Redes Superficiales !!!side:8 También se puede considerar el estudio de las redes superficiales como el estudio de las capas individuales de las redes profundas. Aunque nos interesan las redes profundas, empezaremos por las redes con poca profundidad que, por semejanza, denominaremos **redes superficiales**. Debido a su simplicidad, podemos acercarnos a ellas de forma constructiva y, de paso, adquirir cierta intuición sobre las redes neuronales en general [8]. Consideremos una red ReLU superficial con entrada y salida escalares. Sea $\mathbb{w}=(\mathbb{a},\mathbb{b},\mathbb{c}) \in W=(\mathbb{R}^N)^3$ nuestro conjunto de parámetros para algún $N \in \mathbb{N}$, entonces definimos nuestro modelo $F:\mathbb{R} \times W \to \mathbb{R}$ como \begin{equation} \label{eq:scalarshallownetwork} F(x; \mathbb{w}) := \sum_{i=1}^N c_i \, \operatorname{ReLU}(a_i x + b_i) \end{equation} donde $\sigma$ es la ReLU.  La figura adyacente muestra esta estructura, que en este caso representa una red neuronal superficial $\mathbb{R} \to \mathbb{R}$. En la literatura de aprendizaje profundo, la entrada y la salida de una red a menudo se denominan respectivamente **unidad de entrada** y **unidad de salida**, los valores intermedios suelen denominarse **unidades ocultas**. También se indica lo que comúnmente se denomina **anchura** ($N$) y **profundidad** de la red. !!!teorema:Redes Superficiales ReLU En intervalos compactos las redes neuronales escalares superficiales ReLU calculan exactamente el espacio de funciones lineales a trozos en el intervalo. !!!demo:Demostración Vamos a restringir nuestra demostración al intervalo $[0,1]$, aunque es fácil generalizarlo a cualquier otro intervalo cerrado y acotado. 1. Veamos primero que cualquier función que se calculan con una red neuronal escalar ReLU es lineal a trozos: Por definición, la salida de una red superficial ReLU es una combinación lineal de funciones del tipo: \begin{equation*} x \mapsto \operatorname{ReLU}(a x + b) \end{equation*} Que, dependiendo del valor de $a$, nos da uno de los siguientes tipos de funciones:  Estas tres clases de funciones son funciones lineales a trozos (funciones afines a trozos en realidad), por lo que cualquier combinación lineal de estas funciones sería de nuevo una función lineal a trozos. Por lo tanto, nuestro modelo es en realidad sólo una parametrización particular para las funciones lineales a trozos en $[0,1]$. 2. Comprobemos que cualquier función lineal a trozos sobre $[0,1]$ se puede calcular con una red ReLU superficial. Sea $f:[0,1] \to \mathbb{R}$ una función lineal a trozos con $N$ trozos. Vamos a denotar los puntos de unión entre los diversos trozos lineales con \begin{equation*} 0 = \beta_1 < \beta_2 < \ldots < \beta_{N+1} = 1 \end{equation*} y las pendientes con $\alpha_1, \ldots, \alpha_N$, tal y como ilustra la figura adyacente. Ahora elijamos una red del tipo anterior con $N+1$ neuronas: \begin{equation*} F(x) := \sum_{i=1}^{N+1} c_i \, \operatorname{ReLU}(a_i x + b_i) \end{equation*} y los parámetros $\mathbb{a},\mathbb{b}$ y $\mathbb{c}$ de la red como: \begin{align*} & a_{N+1} = 0, & &b_{N+1} = 1, & &c_1=\alpha_1, \\ & a_1, \ldots, a_N = 1, & &b_i = - \beta_i \ (\text{for } i = 1\ldots N), & &c_i=\alpha_i-\alpha_{i-1} \ (\text{for } i=2\ldots N). \end{align*} Esta elección convierte nuestra red en: \begin{equation} \label{eq:fittedscalarshallow} F(x) = f(0) + \alpha_1 x + \sum_{i=2}^N (\alpha_i - \alpha_{i-1}) \,\operatorname{ReLU}(x-\beta_i) \end{equation} Cuando examinamos el tercer término de \eqref{eq:fittedscalarshallow} vemos que las ReLU harán que cada término sea nulo hasta que $x$ alcance el umbral apropiado, es decir, $\sigma(x-\beta_i) = 0$ hasta que $x>\beta_i$. Por lo tanto, para $x \in [\beta_1,\beta_2]$ obtenemos la función $x \mapsto f(0)+\alpha_1 x$ que coincide exactamente con la función $f$ en ese intervalo. A medida que avanzamos hacia el intervalo $[\beta_2,\beta_3]$ el primer término de la suma de la mano derecha se hace distinto de cero y el modelo se convierte en \begin{align*} x \mapsto &f(0) + \alpha_1 x + (\alpha_2-\alpha_1)(x-\beta_2) \\ &= f(0) + \alpha_1 x - \alpha_1 x + \alpha_1 \beta_2 + \alpha_2(x-\beta_2) \\ &= f(\beta_2) + \alpha_2 (x-\beta_2), \end{align*} que es exactamente $f$ en el intervalo $[\beta_2,\beta_3]$. Podemos seguir avanzando así por el eje $x$ y cada vez que pasemos por cada $\beta_i$ se activará un nuevo término que ajustará la función lineal en los valores correctos. La función, por tanto, puede reescribirse efectivamente como: \begin{equation*} F(x) = \begin{cases} f(0) + \alpha_1 x \quad &\text{si } x \in [\beta_1,\beta_2], \\ f(\beta_2) + \alpha_2 (x-\beta_2) &\text{si } x \in [\beta_2,\beta_3], \\ \qquad \vdots \\ f(\beta_{N-1}) + \alpha_N (x-\beta_{N-1}) &\text{si } x \in [\beta_{N-1},\beta_N], \end{cases} \end{equation*} que coincide exactamente con $f$. Las funciones lineales a trozos son una clase sencilla de funciones, pero pueden utilizarse para aproximar muchas otras clases de funciones hasta un grado arbitrario, como muestra el siguiente lema: !!!teorema:Lema Sea $f \in C([0,1],\mathbb{R})$, entonces para cada $\varepsilon > 0$ existe una función lineal a trozos, $F$, tal que \begin{equation*} \sup_{x\in[0,1]} \left| f(x) - F(x) \right| < \varepsilon \end{equation*} !!!side:9 Se recuerda que la función $\mathbb{\chi}$ es la función característica del conjunto $A$, es decir: $$\mathbb{\chi}_A(x) = \begin{cases} 1 &\text{si } x \in A, \\ 0 &\text{si } x \notin A \end{cases} $$ !!!demo:Demostración Sea $\varepsilon>0$ arbitrario. Como $f$ es una función continua en un dominio compacto, es también uniformemente continua en ese dominio, es decir: \begin{equation*} \exists \delta > 0 \ \forall x_1,x_2 \in [0,1]: |x_1-x_2| < \delta \Rightarrow |f(x_1)-f(x_2)| < \frac{\varepsilon}{2} \end{equation*} Elijamos $N > \frac{1}{\delta}$ y una partición $[0,1]$ por medio de los puntos $x_i = \frac{i}{N}$ para $i=0, \ldots, N$. Definimos una función lineal a trozos $F$ como (es simplemente la poligonal que pasa por los puntos $\{(x_i,f(x_i))\}_{i=0}^N$) [9]: \begin{equation*} F(x) = \sum_{i=1}^N \mathbb{\chi}_{[x_{i-1},x_i)}(x) \left( f(x_{i-1}) + \frac{f(x_i)-f(x_{i-1})}{x_i-x_{i-1}} (x - x_{i-1}) \right) \end{equation*} Obsérvese que para cada $i= 0, \ldots, N$ se tiene que $F(x_i)=f(x_i)$. Sea ahora $x \in [0,1]$ arbitrario. Como $x$ está en algún intervalo de la forma $[x_{i-1},x_i)$, tenemos que: \begin{align*} |f(x)-F(x)| &\leq |f(x)-f(x_i)| + |f(x_i)-F(x)| \\ &< \frac{\varepsilon}{2} + |F(x_i)-F(x)| \\ &< \frac{\varepsilon}{2} + |F(x_i)-F(x_{i-1})| \\ &= \frac{\varepsilon}{2} + |f(x_i)-f(x_{i-1})| \\ &< \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon \end{align*} Como las redes superficiales escalares ReLU representan la función lineal a trozos en $[0,1]$ y esas funciones lineales a trozos son densas en $C([0,1])$ concluimos: !!!teorema:Corolario Las redes neuronales superficiales escalares ReLU de anchura arbitraria son aproximadores universales de $C([0,1])$ con la norma del supremo. La figura adyacente muestra una aproximación sucesiva de la función $\sin(x)$ en un intervalo compacto por medio de una red de anchura creciente de ReLUs. El corolario anterior supone el colofón de un primer resultado de **universalidad**. Este tipo de teoremas se presentan muchas veces como resultados de **densidad**: donde un espacio de funciones, $X$, es denso en otro, $Y$ (hay que tener presenta que no es necesario que $X\subseteq Y$). En el contexto del aprendizaje profundo, la universalidad es el estudio de qué clases de funciones pueden ser aproximadas por arquitecturas particulares de redes neuronales. Obsérvese que el resultado anterior tiene 4 ingredientes: * el tipo de red neuronal (red ReLU escalar superficial), que representa el espacio de funciones $X$; * la dirección de crecimiento de la red (el ancho, es decir, número de neuronas en la capa), que representa los parámetros ajustables de este espacio; * el espacio de la función a aproximar ($C([0,1])$), que representa el espacio de funciones $Y$; * y cómo se mide la aproximación (con la norma del supremo). Generalizar este resultado de aproximación universal a $\mathbb{R}^n$ no es posible con una sola capa, una de las razones por las que son necesarias las redes profundas. En general, las pruebas constructivas, como el lema de densidad anterior no son posibles/disponibles y tendremos que contentarnos con resultados de existencia. La universalidad es teóricamente interesante, ya que nos dice que las redes neuronales pueden, en principio, aproximar bien a la mayoría de los tipos razonables de funciones (continuas, $L^p$, etc.), explicando así en cierta medida por qué son tan potentes. !!!att Pero la universalidad no considera muchas otras facetas importantes de las redes neuronales en la práctica: * ¿cómo escala el número de parámetros con la precisión deseada o con la complejidad de la función?, * en caso de que exista una buena aproximación, ¿cómo de fácil es encontrarla? Aunque se pueden dar más resultados de universalidad, por ahora solo nos importa ver que, bajo algunos supuestos leves, las redes neuronales son aproximadores universales de espacios de funciones muy interesantes. # Descenso por Gradiente !!!note:Contexto del Aprendizaje Supervisado Recordemos que los elementos del Aprendizaje Supervisado que consideramos en esta entrada son: * un dataset $\mathcal{D} = \{ (x_i,y_i)\}_{i=1}^N \subseteq X \times Y$ para algún espacio de entrada $X$ y espacio de salida $Y$; * un modelo $F:X \times W \to Y$ para algún espacio de parámetros $W$; * y una función de pérdida $\ell:Y \times Y \to \mathbb{R}$. La pérdida total en el conjunto de datos para una elección determinada de parámetros: \begin{equation} \label{eq:totaldatasetloss} \ell_{\text{total}}(w) := \frac{1}{|\mathcal{D}|} \sum_{(x,y) \in \mathcal{D}} \ell \left( F(x;w), y \right) \end{equation} Como la pérdida solo depende de los parámetros, también podría incluir algunos términos adicionales de regularización (como se indicó anteriormente), pero vamos a dejar de lado esos detalles por ahora. !!!alg:Descenso por Gradiente Si no tenemos información adicional sobre $F$ no podemos encontrar un mínimo directamente, pero asumiendo que todo es diferenciable podemos usar el **Descenso por Gradiente** como método de aproximación de mínimos: \begin{equation*} w_{t} = w_{t-1} - \eta\, \nabla_{w} \ell_{\text{total}} (w_{t-1}) \end{equation*} donde $\eta > 0$ se denomina **tasa de aprendizaje** y donde elegimos algún $w_0 \in W$ como punto de partida.  Lamentablemente, hacer este cálculo no es práctico en el mundo real debido a: * los datasets suelen ser enormes, * los modelos tienen una enorme cantidad de parámetros. Simplemente calcular $\ell_{\text{total}}$ es ya una gran tarea... intentar calcular $\nabla_w \ell_{\text{total}}$ es algo que, casi con toda probabilidad (salvo casos extremadamente simples, de juguete), está fuera de nuestras opciones. En su lugar, adoptamos un enfoque de divide y vencerás. Dividimos aleatoriamente el conjunto de datos en lotes (aproximadamente) iguales y abordamos el problema lote por lote: !!!alg:Descenso por Gradiente Estocástico Denotemos un lote por un conjunto de índices $I \subset \{ 1 \ldots N \}$, y consideraremos la pérdida en ese único lote: \begin{equation} \label{eq:batchloss} \ell_{I}(w) := \frac{1}{|I|} \sum_{i \in I} \ell \left( F(x_i; w), y_i \right) \end{equation} Si dividimos el conjunto de datos en lotes $I_1,I_2,\ldots, I_B$, entonces podemos dividir nuestro paso de descenso de gradiente en $B$ pasos más pequeños: \begin{equation} \label{eq:gradientdescentupdate} w_{k} = w_{k-1} - \eta\, \nabla_w \ell_{I_k}(w_{k-1}) \end{equation} donde, de nuevo, suponemos algún punto de partida $w_0 \in W$. Cuando llegamos a $k=B$ y hemos agotado todos los lotes decimos que hemos completado una **epoch**. Posteriormente, generamos un nuevo conjunto de lotes aleatorios y repetimos el proceso. Este proceso se denomina **Descenso por Gradiente Estocástico**, o **SGD** para abreviar. Lo de estocástico se refiere a la selección aleatoria de lotes. Si el lote $I$ se extrae uniformemente, entonces: \begin{equation*} \mathbb{E} \left[ \nabla_w \ell_I(w) \right] = \nabla_w \ell_{\text{total}}(w), \end{equation*} es decir, el gradiente de un lote aleatorio extraído uniformemente es un estimador no sesgado del gradiente del conjunto de datos completo. !!!note:Métodos de orden superior El descenso por gradiente (estocástico o no) es un método de primer orden, ya que sólo se basa en las derivadas de primer orden. Los métodos de orden superior rara vez se utilizan con redes neuronales debido a la gran cantidad de parámetros. Un modelo con $N$ parámetros tiene $N$ derivadas de primer orden pero $N^2$ derivadas de segundo orden. Como las redes neuronales suelen tener millones o miles de millones de parámetros, calcular derivadas de segundo orden es normalmente inviable. !!!alg:Momentum Una modificación sencilla, pero importante, del algoritmo de Descenso de Gradiente (estocástico) es el **momentum**: En lugar de dar cada paso basándonos sólo en el gradiente actual, tenemos en cuenta la dirección en la que nos movíamos en los pasos anteriores. El paso de descenso por gradiente modificado viene dado por: \begin{equation*} \begin{split} v_t &= \mu \, v_{t-1} - \eta\,\nabla_w \ell_{I_t}(w_{t-1}), \\ w_t &= w_{t-1} + v_t, \end{split} \end{equation*} donde inicializamos con $v_0 = 0$ y $\mu\in[0,1)$ se llama el coeficiente **momentum**. La variable $v_t$ puede interpretarse como el vector de velocidad actual a lo largo del cual nos movemos en el espacio de parámetros. En cada iteración nuestra nueva velocidad toma una fracción de la velocidad anterior (controlada por $\mu$) y la actualiza con el gradiente actual.  Si $\mu=0$, es decir, sin impulso, volvemos a \eqref{eq:gradientdescentupdate}. Cuanto mayor sea $\mu$ más influencia tiene la historia de los gradientes en nuestro paso actual. # Entrenamiento En la práctica, el proceso de entrenamiento implica algo más que aplicar SGD a todo el conjunto de datos. Una cosa que tenemos que tener en cuenta es que $\mathcal{D}$ es la única información real que tenemos sobre la función subyacente que estamos tratando de aproximar, por lo que no hay manera de juzgar cómo de buena será la aproximación conseguida fuera de él. Como sabemos que las redes neuronales son aproximadores universales, siempre podemos encontrar una red neuronal que se ajuste perfectamente a cualquier conjunto de datos, por lo que el sobreajuste es un hecho que perjudica nuestro objetivo real. !!!att Lo que realmente buscamos es la generalización: la capacidad de nuestra red neuronal para dar la salida correcta a entradas que no ha visto antes. Una sencilla solución que se usa (no solo en redes neuronales, sino en todos los procesos de aprendizaje automático) consiste en dividir el conjunto de datos en dos partes y utilizar sólo una parte para entrenar la red. La parte restante (que la red nunca ha visto durante el ajuste de los parámetros) se utilizará posteriormente para comprobar la capacidad de generalización de la red modificada. La división exacta depende de la situación, pero una buena regla es utilizar el 80% del conjunto de datos para el entrenamiento y el 20% para las pruebas. !!!alg Denotemos nuestros conjuntos de datos de entrenamiento y de test como: \begin{equation*} \mathcal{D}_{\text{train}} , \mathcal{D}_{\text{test}} \subset \mathcal{D} \end{equation*} A continuación, realizamos el SGD en el conjunto de datos de entrenamiento, es decir, intentamos minimizar la pérdida en los datos de entrenamiento: \begin{equation} \label{eq:trainingloss} \ell_{\text{train}}(w) := \frac{1}{|\mathcal{D}_{\text{train}}|} \sum_{(x,y) \in \mathcal{D_{\text{train}}}} \ell(F(x;w),y) \end{equation} Pero juzgamos el rendimiento de nuestra red por las pérdidas en los datos de test: \begin{equation} \label{eq:testingloss} \ell_{\text{test}}(w) := \frac{1}{|\mathcal{D}_{\text{test}}|} \sum_{(x,y) \in \mathcal{D_{\text{test}}}} \ell(F(x;w),y) \end{equation} Controlando las pérdidas de test durante el entrenamiento podemos juzgar durante cuánto tiempo debemos entrenar, lo bien que generaliza nuestra red y cuándo se produce el sobreajuste. La figura adyacente ilustra el comportamiento típico de las curvas de pérdidas que se encuentran durante el entrenamiento: la pérdida de entrenamiento convergerá generalmente a un valor muy bajo, y a veces la pérdida de test se comporta de manera similar y converge también pero a un valor más alto, como se ilustra a la izquierda. Podría ocurrir que la pérdida de test empiece a aumentar de nuevo en algún momento, como a la derecha, lo que indica un sobreajuste, momento que puede indicar que debemos parar el entrenamiento porque es lo mejor que vamos a conseguir con el modelo actual. !!!side:10 Los hiperparámetros son todos los parámetros que seleccionamos nosotros mismos y no son partes entrenables del modelo. Algunos ejemplos son: tamaño del lote, tasa de aprendizaje, tamaño del modelo, elección de la función de activación, proporción de división del conjunto de datos, etc. Pero el problema puede que no se solucione solo con la división anterior, ya que cuando estamos diseñando una red para una aplicación determinada solemos hacer entrenamientos repetidos mientras hacemos pruebas con los *hiperparámetros* [10] para intentar mejorar la pérdida en el conjunto de test. Esto puede llevarnos a sobreajustar los hiperparámetros al conjunto de datos de test dado. En este caso, hay dos cosas que podemos hacer para mitigarlo: * dividir el conjunto de datos en tres partes: entrenamiento/test/validación,  * rehacer la división aleatoriamente cada vez que volvemos a entrenar. Habitualmente, el segundo método es preferible, ya que es más fácil de implementar e incluso si se utiliza el primer método, sigue siendo necesario rehacer la división si decidimos hacer algunos cambios después de haber utilizado el conjunto de datos de validación (ya que si lo utilizamos más de una vez, volvemos al punto de partida). # Bibliografía [#bekkers2021]: Bekkers, Erik J (2021). B-Spline CNNs on Lie Groups. arXiv: 1909.12057 [cs.LG]. [#cohen2016]: Cohen, Taco and Max Welling (2016). “Group Equivariant Convolutional Networks”. In: International Conference on Machine Learning. PMLR, pp. 2990–2999. [#cohen2020]: Cohen, Taco, Mario Geiger, and Maurice Weiler (2020). A General Theory of Equivariant CNNs on Homogeneous Spaces. arXiv: 1811.02017 [cs.LG]. [#duchi2011]: Duchi, John, Elad Hazan, and Yoram Singer (2011). “Adaptive subgradient methods for online learning and stochastic optimization.” In: Journal of Machine Learning Research 12.7. [#federer2014]: Federer, Herbert (2014). Geometric Measure Theory. Springer. isbn: 978-3-540-60656-7. doi: 10.1007/978-3-642-62010-2. [#fukushima1987]: Fukushima, Kunihiko (1987). “Neural network model for selective attention in visual pattern recognition and associative recall”. Applied Optics 26.23, pp. 4985–4992. [#glorot2010]: Glorot, Xavier; Yoshua Bengio (2010). “[Understanding the difficulty of training deep feed forward neural networks](https://proceedings.mlr.press/v9/glorot10a.html)”. Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics. Ed. by Yee Whye Teh and Mike Titterington. Vol.9. Proceedings of Machine Learning Research. Chia Laguna Resort, Sardinia, Italy: PMLR, pp. 249–256. [#golan1999]: Golan, Jonathan S. (1999). Semirings and their Applications. Dordrecht: Springer Netherlands. isbn: 978-90-481-5252-0. doi: 10.1007/78-94-015-9333-5. url: http://link.springer.com/10.1007/978-94-015-9333-5. [#he2015]: He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun (2015). Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. arXiv: 1502.01852 [cs.CV]. [#ivakhnenko1966]: Ivakhnenko, Aleksei Grigorevich; Valentin Grigorevich Lapa (1966). Cybernetic predicting devices. Tech. rep. Purdue Univ Lafayette Ind School of Electrical Engineering. [#kingma2017]: Kingma, Diederik P. and Jimmy Ba (2017). Adam: A Method for Stochastic Optimization. arXiv: 1412.6980 [cs.LG]. [#kolokoltsov1997]: Kolokoltsov, Vassili N. and Victor P. Maslov (1997). Idempotent Analysis and Its Applications. Dordrecht: Springer Netherlands. isbn: 978-90-481-4834-9. doi: 10.1007/978-94-015-8901-7. url: http://link.springer.com/10.1007/978-94-015-8901-7. [#krizhevsky2012]: Krizhevsky, Alex, Ilya Sutskever, Geoffrey E Hinton (2012). “[ImageNet Classification with Deep Convolutional Neural Networks](https://proceedings.neurips.cc/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf)”. Advances in Neural Information Processing Systems. Ed. by F. Pereira, C.J. Burges, L. Bottou, and K.Q. Weinberger. Vol. 25. Curran Associates, Inc. [#lecun1998]: LeCun, Yann; Léon Bottou; Yoshua Bengio; Patrick Haffner (1998). “Gradient-based learning applied to document recognition”. In: Proceedings of the IEEE 86.11, pp. 2278–2324. [#lecun1989]: LeCun, Yann; Bernhard Boser, John S Denker, Donnie Henderson, Richard E Howard, Wayne Hubbard, Lawrence D Jackel (1989).“Backpropagation applied to handwritten zipcode recognition”. Neural computation 1.4, pp. 541–551. [#lee2010]: Lee, John M. (2010). Introduction to Topological Manifolds. 2nd ed. Graduate Texts in Mathematics. Springer. isbn: 978-1-4419-7939-1. doi: 10.1007/978-1-4419-7940-7. [#lee2013]: Lee, John M. (2013). Introduction to Smooth Manifolds. 2nd ed. Graduate Texts in Mathematics. Springer. isbn: 978-1-4419-9981-8. doi: 10.1007/978-1-4419-9982-5_1. [#mcculloch1943]: McCulloch, Warren S; Walter Pitts (1943). “A logical calculus of the ideas immanent in nervous activity”. The bulletin of mathematical biophysics 5.4, pp. 115–133. [#oh2004]: Oh, Kyoung-Su; Keechul Jung (2004). “GPU implementation of neural networks”. Pattern Recognition 37.6, pp. 1311–1314. [#tao2011]: Tao, Terence (2011). An Introduction to Measure Theory. Vol. 126. Graduate Studies in Mathematics. American Mathematical Society. isbn: 978-1-4704-6640-4. doi: 10.1090/gsm/126. [#tieleman2012]: Tieleman, Tijmen, Geoffrey Hinton, et al. (2012). “Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude”. In: Coursera: Neural networks for machine learning 4.2, pp. 26–31. (insert ../menu.md.html here)