**PSO: Optimización por enjambres de partículas** La **Optimización por Enjambres de Partículas** (conocida como **PSO**, por sus siglas en inglés, **Particle Swarm Optimization**) es una técnica de optimización/búsqueda. Aunque normalmente PSO se usa en espacios de búsqueda con muchas dimensiones, los ejemplos que se mostrarán aquí harán uso de un espacio bidimensional, con el fin de facilitar la visualización, y porque nuestro objetivo es puramente didáctico, esperando que el interesado no encuentre dificultades en extenderlo a otros casos (la librería proporcionada en el [repositorio de la asignatura](https://github.com/fsancho/IA) se adapta al número de dimensiones que se necesite). !!!side:1 Kennedy, J. & Eberhart, R. (1995), *Particle swarm optimization*, Neural Networks, 1995. Proceedings., IEEE International Conference. ![](./img/abeja.jpg align="left" width=300px)Este método fue descrito alrededor de 1995 por Kennedy y Eberhart [1], y se inspira en el comportamiento de los enjambres de insectos en la naturaleza. En concreto, podemos pensar en un enjambre de abejas, ya que éstas a la hora de recolectar polen buscan la región del espacio en la que existe más densidad de flores, porque la probabilidad de que haya polen es mayor. La misma idea fue trasladada al campo de la computación en forma de algoritmo y se emplea en la actualidad en la optimización de distintos tipos de sistemas. !!!side:2 A la función de fitness a veces también se le llama **paisaje de fitness**, ya que puede verse como un paisaje con valles y colinas formados por los valores que toma la función. Formalmente hablando, se supone que tenemos una función desconocida, $f(x_1, \dots, x_n)$, que podemos evaluar en los puntos que queramos pero a modo de caja negra, por lo que no podemos conocer su expresión. El objetivo es el habitual en optimización, encontrar valores de $x_1, \dots, x_n$ para los que la función $f$ sea máxima (o mínima, o bien verifica alguna relación extremal respecto a alguna otra función). Como ya hemos visto en otras situaciones similares, a $f$ se le suele llamar **función de fitness** [2], ya que va a determinar cómo de buena es la posición actual para cada partícula. !!!side:3 Como es de esperar, para la mayoría de los espacios de búsqueda este método es altamente ineficiente, por lo que es imprescindible encontrar otros métodos más *inteligentes* que, a pesar del desconocimiento de la función a optimizar, ofrezcan más posibilidades de éxito que la simple búsqueda aleatoria. Una primera aproximación para resolver este problema de calcular valores extremales de una función podría ser la selección aleatoria de valores de sus variables $x_1,\dots,x_n$, y almacenar el mayor de los resultados encontrados, lo que se conoce como una **búsqueda aleatoria** [3]. La idea que vamos a seguir en PSO comienza de forma similar, situando partículas al azar en el espacio de búsqueda, pero dándoles la posibilidad de que se muevan a través de él de acuerdo a unas reglas que tienen en cuenta el conocimiento personal de cada partícula y el conocimiento global del enjambre. Veremos que proporcionándoles una capacidad simple de movimiento por este _paisaje_ y de comunicación entre ellas pueden llegar a descubrir valores particularmente altos para $f$ gastando pocos recursos computacionales (cálculo, memoria y tiempo).  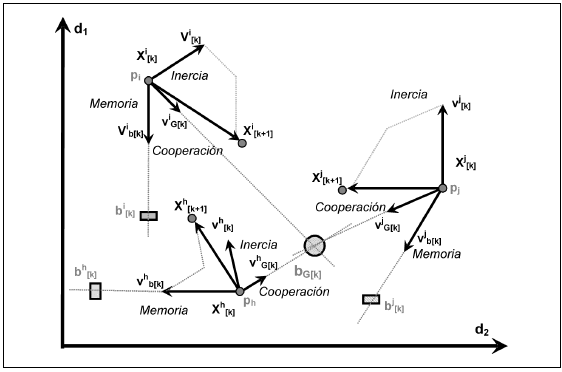# Funcionamiento de PSO Cada partícula (individuo) tiene una **posición**, $\vec{p}$ (que en 2 dimensiones vendrá determinado por un vector de la forma $(p_x, p_y)$), en el espacio de búsqueda y una **velocidad**, $\vec{v}$ (que en 2 dimensiones vendrá determinado por un vector de la forma $(v_x, v_y)$), que determina su movimiento a través del espacio. Además, como partículas de un mundo real físico, tienen una cantidad de **inercia**, $w$, que los mantiene en la misma dirección en la que se movían, así como una aceleración (cambio de velocidad), que depende principalmente de dos características: 1. Cada partícula es atraída hacia la mejor localización que ella, personalmente, ha encontrado en su historia ($p_i^{best}$). 2. Cada partícula es atraída hacia la mejor localización que ha sido encontrada por el conjunto de partículas en el espacio de búsqueda ($p_{gbest}$).  La fuerza con que las partículas son empujadas en cada una de estas direcciones depende de dos parámetros que pueden ajustarse ($c_1$ y $c_2$) de foma que, a medida que las partículas se alejan de estas localizaciones mejores, la fuerza de atracción es mayor. También se suele incluir un factor aleatorio que influye en cómo las partículas son empujadas hacia estas dos localizaciones ($r_1$ y $r_2$). Formalmente, para la partícula $i$-ésima lo podemos escribir como una dependencia temporal de la siguiente forma: $$v_i(t+1)= w \cdot v_i(t) + c_1\cdot r_1\cdot (p_i^{best}-p_i(t)) + c_2 \cdot r_2 \cdot (p_{gbest}-p_i(t))$$ Una vez actualizadas las velocidades de todas las partículas, sus posiciones se actualizan siguiendo una ley simple: $$p_i(t+1)=p_i(t)+v_i(t)$$  !!!side:4 En uno de los modelos que puedes encontrar en los [recursos del curso de IA](https://github.com/fsancho/IA), y solo a modo de ejemplo, se intenta optimizar una función que viene determinada por los valores sobre una malla. El **paisaje** se obtiene asignando aleatoriamente valores a cada uno de los puntos de la malla, para posteriormente aplicar un proceso de difusión que suaviza los valores obtenidos, lo que proporciona un espacio con numerosos mínimos locales (valles) y máximos locales (colinas), por lo que su optimización por medios más clásicos (como el ascenso de la colina) es dificultosa. Esta función ha sido creada así solo con fines ilustrativos, ya que habitualmente en aplicaciones reales de PSO la posición de las partículas pueden corresponderse con parámetros diversos del problema (por ejemplo, de predicción de un mercado de valores), y la función no tendrá las restricciones ni características que aquí se imponen (en el mismo ejemplo, podría evaluarse por medio de los datos históricos). El algoritmo PSO se esboza a grandes rasgos en el siguente código [4]: ``` Asignar posiciones y velocidades aleatorias iniciales a las partículas Repetir Cada partícula: Actualizar su velocidad considerando: Inercia de la partícula (la hace seguir con la misma velocidad) Atracción al mejor personal Atracción al mejor global Actualizar la posición de la partícula Calcular el valor de fitness en la nueva posición Actualizar su mejor personal Actualizar el mejor global del sistema Devolver el mejor global ``` Lo interesante de este modelo es que cada partícula solo hace operaciones vectoriales básicas (para actualizar las velocidades y posiciones basta realizar algunas sumas de vectores) y, como la experiencia muestra que hacen falta pocas partículas y el número de iteraciones es bajo, la complejidad del proceso se centra sobre todo en la evaluación del fitness de cada partícula en cada iteración, algo que no puede evitarse y que depende exclusivamente del problema específico que se quiera optimizar. En consecuencia, este método de optimización es especialmente adecuado cuando el coste de la función de fitness es muy elevado, pues requiere pocas evaluaciones para encontrar valores cercanos al óptimo. Como inconveniente, no podemos estar seguros de alcanzar el óptimo global, como pasa en todo este tipo de metaheurísticas (problema que comparten todos los métodos de optimización que trabajan con cajas negras). # Variantes Realmente, se puede enriquecer el modelo añadiendo comportamientos diversos a los individuos-partículas, ya sea inspirándose en comportamientos observados en la naturaleza o puramente abstractos. !!!side:5 Lo que supone acabar prematuramente en un máximo local, y con pocas opciones de escapar de él para encontrar mejores optimizaciones. Una primera posibilidad, que se implementa en algunos de los algoritmos que se engloban dentro de los PSO, y que es fácil de implementar en el modelo anterior, consiste en añadir una **fuerza repulsiva entre las partículas** para intentar prevenir que todas ellas converjan prematuramente a una pequeña zona del espacio de búsqueda [5]. De esta forma, si dos partículas se aproximan demasiado, sufrirán una fuerza de repulsión que las separa entre sí (y las aleja de la zona de encuentro). !!!side:6 También suele considerarse el caso en que una misma partícula pertenezca a más de una familia, lo que permite que haya comunicaciones a larga distancia entre muchas partículas aunque no pertenezcan a la misma familia. Otra opción es no considerar el máximo global que se va encontrando, sino **dividir las partículas en familias** y considerar máximos globales por familias. De esta forma, cada familia puede trabajar en paralelo y cada partícula solo ha de tener conocimiento acerca de lo que *sucede* en su familia, no en el conjunto global de individuos. Además, existen variantes en las que estas familias son dinámicas, de forma que las partículas pueden ir cambiando de familia a medida que el algoritmo se ejecuta [6]. Por último, ¿qué pasa si la función que intenta ser optimizada cambia en el tiempo?, es decir, en el caso en que sea una **búsqueda dinámica** donde la variación de la función durante el tiempo de ejecución haga que los extremos se vayan desplazando por el espacio de búsqueda. No resulta difícil modificar el modelo anterior para que se genere una función cambiante en el tiempo y poder así experimentar bajo qué condiciones las partículas del enjambre siguen el movimiento de los máximos a medida que se trasladan por el espacio. (insert menu.md.html here)