**Sistemas Dinámicos** ![](img/pendulo.gif align="right" width=20%) Como disciplina matemática, el estudio de los sistemas dinámicos se originó muy probablemente a finales del siglo XIX a través de los trabajos de Henri Poincare en su estudio de la mecánica celeste. Una vez formuladas las ecuaciones que describen el movimiento de los planetas alrededor del sol (es decir, una vez construido el modelo matemático), la búsqueda de soluciones como medio para describir el movimiento de los planetas y hacer predicciones de las posiciones en el tiempo es el siguiente paso. Pero cuando la búsqueda de soluciones a conjuntos de ecuaciones es aparentemente demasiado complicada o imposible, a uno le queda el estudio de la estructura matemática del modelo para acotar de alguna manera y de forma creativa las posibles funciones de solución. Esta idea de estudiar la naturaleza y la estructura de las ecuaciones de un modelo matemático en busca de pistas sobre la naturaleza y la estructura de sus soluciones es la idea general que subyace a las técnicas y la teoría de lo que ahora llamamos **sistemas dinámicos**. Con más de 100 años de antigüedad, el concepto matemático de sistema dinámico es una idea relativamente nueva. Y puesto que, así definido, se trata realmente de un estudio centrado en la naturaleza de las funciones de (normalmente) una única variable independiente real, es una subdisciplina de lo que los matemáticos llaman análisis real. Sin embargo, se puede decir que los sistemas dinámicos extraen su teoría y sus técnicas de muchas áreas de las matemáticas, desde el análisis hasta la geometría y la topología, pasando por el álgebra. Podríamos llamar a áreas matemáticas como la geometría, la topología y la dinámica matemáticas de segunda generación, ya que tienden a tender un puente con otras áreas más puras en sus teorías. Pero como estudio de lo que significa realmente modelar fenómenos mediante funciones y ecuaciones, a veces se denomina a los sistemas dinámicos como el estudio matemático de cualquier concepto matemático que evoluciona con el tiempo. Así pues, para definir este concepto con mayor precisión, comenzamos con una afirmación que podría ser la más general y, sin embargo, la menos útil: # Aproximación informal !!!alg Un sistema dinámico es una formalización matemática de cualquier regla fija que describa la dependencia de la posición de un punto en algún espacio ambiente con respecto a un parámetro. !!!side:1 A veces, el parámetro puede tomar valores en espacios mucho más generales, por ejemplo, subconjuntos de $\mathbb{C}$, $\mathbb{R}^n$, cuaterniones o, en general, cualquier conjunto con estructura de grupo algebraico. Sin embargo, en términos clásicos, un sistema dinámico implica realmente un parámetro que toma valores sólo en un subconjunto de $\mathbb{R}$. !!!side:2 Una **topología** confiere a un conjunto la propiedad matemática de espacio; dota a los elementos de un conjunto de una noción de proximidad entre ellos y permite que las funciones sobre un con punto tengan propiedades como continuidad, diferenciabilidad, etc. !!!def: Elementos de un Sistema Dinámico Tenemos los siguientes elementos en un Sistema Dinámico: 1. El parámetro aquí, usualmente referido como **tiempo** debido a su referencia a la aplicación en las ciencias, toma valores numéricos. Por lo general, estos valores pueden ser [1]: *discretos* (como los números naturales, $\mathbb{N}$, o los enteros, $\mathbb{Z}$), o *continuos* (definidos por medio de algún intervalo en $\mathbb{R}$). 2. El espacio ambiente tiene un **estado** en el sentido de que todos sus puntos tienen una *posición* marcada que puede cambiar al variar el parámetro. En este espacio, cada punto tiene una posición relativa a los demás puntos y un conjunto completo de coordenadas (generalizadas) en el espacio suele proporcionar esta noción de posición. Fijando las coordenadas y permitiendo que el parámetro varíe, se puede crear una relación funcional entre los puntos en un valor del parámetro y los de otro valor del parámetro. En general, esta noción de posiciones relativas de puntos en un espacio y de relaciones funcionales en ese espacio implica la noción de **topología** en un conjunto [2]. 3. A este espacio ambiente lo llamaremos el **espacio de estados**: el conjunto de todos los estados posibles en los que puede estar un sistema dinámico para cualquier valor de los parámetros (en cualquier momento del tiempo). 3. La regla fija suele ser un mecanismo para pasar de un estado al siguiente en el orden especificado por el parámetro: * Para los *sistemas dinámicos discretos*, a menudo se da como una función que lleva cada punto del espacio de estados a su *siguiente* estado. Los estados futuros de un estado se obtienen por la aplicación sucesiva de la función. Si es posible, los estados pasados de un estado pueden encontrarse aplicando la inversa de la función. De esta forma, se define el sistema dinámico de forma recursiva a través de la función. * En los *sistemas dinámicos continuos*, en los que es más complicado definir cuál puede ser el sucesor del estado en un valor del parámetro, la relación entre estados del espacio puede definirse mediante una ecuación diferencial, igual a la de la función en un sistema discreto, en el sentido de que describe implícitamente el método para pasar de un estado al siguiente (pero definido infinitesimalmente). La solución de una EDO (o de un sistema de EDO's) sería una función cuyo dominio contiene los puntos del espacio de estados y el parámetro, y que toma valores en el espacio de estados (el codominio). A menudo, esta última función se denomina **evolución del sistema**, proporcionando una forma de pasar de cualquier estado particular a cualquier otro estado alcanzable desde ese estado inicial a través de un valor del parámetro. Aunque se puede demostrar que dicha función siempre existe, y a menudo se pueden estudiar sus propiedades, en general NO será conocida a priori, y muchas veces ni siquiera es expresable a posteriori. !!!note Es habitual en este ámbito de las matemáticas que los términos **regla fija** y **evolución** se utilicen más o menos indistintamente, y que ambos se refieran a los mismos objetos sin distinción. Sin embargo, se podría hacer una sutil diferencia: la regla fija seguirá siendo la receta definida recursivamente para el movimiento dentro de un sistema dinámico, y la evolución se reservará para la forma funcional del movimiento de los puntos. Así, la EDO es simplemente la regla fija, mientras que la solución general, si se puede encontrar, es la evolución, por ejemplo. Aunque esta idea de sistema dinámico es demasiado general para ser útil, es instructiva. Pero antes de crear una definición más constructiva, veamos algunos ejemplos clásicos en las próximas secciones. # Ejemplos de Sistemas Dinámicos ## Ecuaciones diferenciales ordinarias (EDO) !!!def: Solución de un EDO Dada la EDO autónoma de primer orden (vectorial) \begin{equation} \label{edo} \mathbf{x}' = f(\mathbf{x}) \end{equation} una solución, si existe, es un vector de funciones $\mathbf{x}(t) = [x_1(t), x_2(t),\dots, x_n(t)]$ parametrizado por una variable real $t\in \mathbb{R}$ donde el dominio común de las funciones coordenadas es algún subintervalo de $\mathbb{R}$. Recordemos que una forma bastante general para sistemas de primer orden de EDOs es $x' = f(x,t)$, con la variable independiente $t$ representada explícitamente en el lado derecho. Una EDO (o sistema) se denomina **autónoma** si $t$ no está representada explícitamente, y **no autónoma** cuando $t$ está explícita en la EDO. Por ejemplo, $x' = \frac{tx^2}{4} = f(x,t)$ es no autónoma, mientras que $x' = \frac{x}{4} = f(x)$ es autónoma. A veces también llamamos a los sistemas autónomos **invariantes en el tiempo** cuando la variable independiente representa realmente el tiempo. La propiedad importante de una EDO autónoma es que las leyes del movimiento en cualquier punto del tiempo son las mismas que en cualquier otro punto del tiempo; las leyes del movimiento son invariantes bajo traslaciones en el tiempo. Si un sistema de primer orden como el anterior es autónomo, entonces el lado derecho representa un campo vectorial en el espacio de estados que no cambia en el tiempo, lo que significa que el paso de un estado al siguiente será el mismo sin importar cuándo. Con el tiempo explícito en la función $f(x,t)$, el campo vectorial cambiaría a medida que avanza el tiempo. !!!side:3 Hay que tener cuidado de no confundir un espacio de estados, el espacio de todos los estados posibles de un sistema, con el espacio de configuración. Por ejemplo, el conjunto de todas las posiciones de un péndulo es simplemente el círculo. Este sería el espacio de todas las configuraciones posibles. Sin embargo, su espacio de estados incluye tanto la posición del péndulo como su velocidad, la información necesaria para determinar el sistema en cada momento. Según la definición que dimos de los sistemas dinámicos, en un sistema autónomo dado por la EDO anterior, tenemos que: * La propia EDO es la regla fija, que describe la forma de pasar de un estado al siguiente mediante un cambio infinitesimal en el valor del parámetro $t$. Resolver la EDO significa encontrar la función desconocida $\mathbf{x}(t)$, que al venir dada como una forma integral podrá ser determinada en el mejor de los casos salvo constante. La inclusión de datos iniciales proporciona un estado inicial de las variables del sistema que podrá determinar estas constantes, lo que convierte al sistema en un **Problema de Valor Inicial**. La solución de este tipo de problemas para valores válidos de $t$ proporciona los *otros* estados que puede alcanzar el sistema (hacia adelante o hacia atrás en el tiempo) en comparación con el estado inicial. Encontrar la expresión que determina las constantes de integración de la solución general de la EDO en términos de las variables de datos iniciales es determinar la evolución. * Este tipo de sistema dinámico se llama **continuo**, ya que el parámetro $t$ tomará valores en algún dominio (normalmente, un intervalo con interior no vacío) en $\mathbb{R}$. Los sistemas dinámicos como este que surgen de las EDOs también se llaman **flujos**, ya que las distintas soluciones del problema de valor inicial se parecen a las líneas de flujo de un fluido. * En este ejemplo particular, el espacio de estado es el espacio $n$-dimensional parametrizado por las $n$ variables que componen el vector $\mathbf{x}(t)$ [3]. Independientemente de las propiedades del espacio de estados, las soluciones pueden verse como curvas parametrizadas, que suelen llamarse **trayectorias**. También llamamos a este espacio de estados el **espacio de fase**. ## Mapas Dado cualquier conjunto, $X$, y una función, $f: X \to X$, se puede construir un sistema dinámico simplemente aplicando la función $f$ una y otra vez a $X$. Cuando $X$ es un espacio topológico (lo que nos da una noción matemáticamente precisa de una relación de proximidad), podemos entonces discutir si la función $f$ es continua o no, en cuyo caso se llama **mapa** (o **cascada**). * Siempre trabajaremos con espacios topológicos, pero detallaremos la topología sólo cuando sea necesario. Muchas veces, los espacios de estado más comunes serán como subconjuntos del espacio real $\mathbb{R}^n$. En este caso, una de esas nociones de cercanía de puntos será el resultado de una definición precisa de una distancia entre puntos dada por una métrica. * La regla fija es la función $f$. * De manera puramente formal, $f$ define la evolución (recursivamente) por composición consigo misma: si $x\in X$, definimos $x_0 = x$, y $x_1 = f(x_0)$, y en general $x_n=f(x_{n-1})$ para todo $n\in\mathbb{N}$.  !!!side:4 Hay una gran relación entre el concepto de fractal y las construcciones obtenidas por sistemas dinámicos. * ![](img/julia.gif width="30%" align=right)Los mapas son ejemplos de **sistemas dinámicos discretos**. Algunos de sus ejemplos más famosos son las construcciones fractales como los *conjuntos de Julia* y *de Mandelbrot* que surgen de mapas sobre $\mathbb{C}$ [4]. ## Dinámica simbólica ![](img/psection.gif align="right" width=150px)Dado un conjunto de símbolos $M = \{A,B,C,\dots\}$, consideremos el *espacio* de todas las secuencias bi-infinitas de estos símbolos (infinitas en ambas direcciones): $$\Omega_M = \{(\dots,x_{-2},x_{-1},x_0,x_1,x_2,\dots):\ i\in \mathbb{Z},\ x_i \in M\}=\{g:\mathbb{Z}\to M\}=M^{\mathbb{Z}}$$ !!!side:5 Siempre podemos considerar este conjunto (muy grande) de secuencias infinitas como un espacio una vez se le dote de una topología. Esto implicaría definir subconjuntos abiertos para este conjunto, y podemos hacerlo mediante $\epsilon$-bolas definiendo una noción de distancia entre secuencias (una métrica). Como está expresado, se puede considerar $\Omega_M$ como el espacio de todas las funciones de $\mathbb{Z}$ a $M$: cada función es sólo una asignación de un elemento de $M$ a cada entero de $\mathbb{Z}$ [5]. Y podemos considerar funciones que iterar de forma muy sencilla, por ejemplo, los *desplazamientos*, que llevan secuencias en secuencias: si $\mathbf{x}\in\Omega_M$, entonces $(f(\mathbf{x}))_n=\mathbf{x}_{n+1}$.  Una forma de obtener este tipo de sistemas dinámicos es a partir de otro sistema dinámico anterior en el que $M$ son regiones del espacio que se transforman entre sí. De esta forma, estudiamos cómo funcionan las regiones bajo la acción de la regla original, miramos el sistema a un nivel de detalle más grueso, no puntualmente, y el nuevo sistema dinámico simbólico permite estudiar las propiedades del original de forma más sencilla. ## Otros ejemplos interesantes ### Billar !!!side:6 Es decir, la *energía cinética total* y el *momento total* de las partes constituyentes se conservan en cada colisión, por lo que la energía puede transferirse entre las masas puntuales en una colisión, no se absorbe energía, ni por una pared ni por otra masa. Consideremos dos masas puntuales de masa $m$ que se mueven a velocidades constantes (posiblemente diferentes) a lo largo de un cable tensado, de longitud finita, conectando dos paredes. Supondremos que las colisiones son perfectamente elásticas tanto entre las masas como con las paredes [6]. Obsérvese que esto implica que, aunque la velocidad de una masa puede invertir su dirección a veces (tras una colisión con una pared, por ejemplo) o cambiar con la velocidad de la otra masa (cuando las masas chocan), realmente sólo hay unas pocas velocidades distintas que pueden tomar las masas en este sistema. Por ello, la velocidad de las masas no es realmente una variable necesaria para representar el estado del sistema, y el espacio de estados es sólo el conjunto de todas las posiciones de las masas. Sin embargo, las velocidades sí juegan un papel fundamental en el movimiento alrededor del espacio de estados. Si se parametriza el cable como un intervalo cerrado y acotado en $\mathbb{R}$, y se toma la posición de cada masa como coordenada, el espacio de estados es simplemente un triángulo en el plano, es un buen ejercicio intentar analizar a qué situaciones corresponden los vértices de este triángulo, sus lados, y cómo se describe en este espacio el movimiento de las bolas a lo largo del cable,... en otras palabras, estudiar cómo evoluciona el sistema dinámico. Para unas velocidades $v_1$ y $v_2$ iniciales dadas, se puede intentar describir el movimiento en el espacio de estados dibujando una trayectoria representativa para los casos: * $v_1 = 0$, $v_2 \neq 0$. * $\frac{v_1}{v_2}$ un número racional. * $\frac{v_1}{v_2}$ un número irracional. 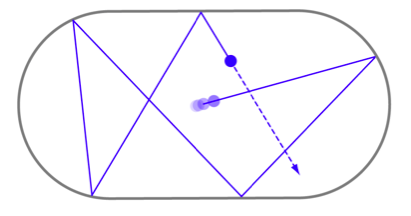Si consideremos ahora una masa puntual que se mueve a velocidad constante dentro de una región cerrada y acotada de $\mathbb{R}^2$, en la que la frontera es lisa y las colisiones con la frontera son especulares (lo que significa que el ángulo de incidencia es igual al ángulo de reflexión) podemos plantear algunas preguntas:  * ¿Cómo afecta la forma de la región a los tipos de trayectorias que puede recorrer la masa? * ¿Existen trayectorias cerradas (periódicas)? * ¿Puede haber una trayectoria densa (que se acerque arbitrariamente a cualquier punto de la región)? Existe un método para estudiar el tipo de sistema dinámico llamado [**billar**](https://plus.maths.org/content/chaos-billiard-table) creando un sistema dinámico discreto para registrar el movimiento y recogiendo sólo la información esencial. En este sistema dinámico discreto, independientemente de la forma de la región, el espacio de estados es un cilindro. ### Recurrencias de orden superior !!!side:7 También conocido como **Fibonacci**. Los mapas como sistemas dinámicos son ejemplos de recursiones de primer orden, ya que para $f: X \to X$, $x_n = f(x_{n-1})$ y cada elemento de una secuencia sólo depende del elemento anterior. Los *Conejos de Leonardo de Pisa* [7] son un bello ejemplo de un tipo de crecimiento que no es exponencial, sino algo llamado **asintóticamente exponencial**: colocamos una pareja de conejos reproductores recién nacidos en un entorno cerrado. Los conejos de esta especie producen otra pareja de conejos cada mes después de ser fértiles (y nunca mueren ni experimentan la menopausia). Cada nueva pareja de conejos (de nuevo, sin tener en cuenta las cuestiones de incesto, género y ADN) se vuelve fértil después de un mes y empieza a producir cada mes a partir del segundo. ¿Cuántos conejos hay después de 10 años? Mes|$a_n$|$j_n$|$b_n$|Parejas :---:|:---:|:---:|:---:|:---: 1| 0| 0| 1| 1 2| 0| 1| 0| 1 3| 1| 0| 1| 2 4| 1| 1| 1| 3 5| 2| 1| 2| 5 6| 3| 2| 3| 8 7| 5| 3| 5| 13 A partir de esta tabla podemos extraer una forma de elaborar una expresión que indique el número de parejas al final de un mes cualquiera: empezamos con $r_n$, el número de parejas de conejos en el mes $n$. Los conejos pueden ser de tres posibles tipos: Adultos ($a_n$), jóvenes ($j_n$) y recién nacidos ($b_n$), de modo que $r_n = a_n + j_n + b_n$, y se verifican las siguientes relaciones: 1. $b_{n+1} = a_n + j_n$ 2. $a_{n+1} = a_n + j_n$. 3. $j_{n+1} = b_n$. Por tanto: $r_n = a_n + j_n + b_n = (a_{n-1} + j_{n-1}) + b_{n-1} + (a_{n-1} + j_{n-1})$. Como $a_{n-1} = a_{n-2} +j_{n-2}$ y $j_{n-1} = b_{n-2}$, podemos obtener que: $r_n = a_{n-1} + j_{n-1} + b_{n-1} + a_{n-2} + j_{n-2} + b_{n-2} = r_{n-1} + r_{n-2}$. Por tanto, el patrón se rige por una recursión de segundo orden $r_n = r_{n-1} + r_{n-2}$ con datos iniciales $r_0 = r_1 = 1$. Al ser una recursión de segundo orden, no podemos pasar al siguiente estado desde un estado actual sin conocer también el estado anterior. Este es un ejemplo de un modelo que no es un sistema dinámico como se ha dicho. Podemos convertirlo en uno (de la misma manera que se utilizaría para convertir una EDO de orden superior en un sistema de primer orden), pero necesitaremos un poco más de estructura. # Definición Formal Ya podemos dar una definición mucho más precisa y útil de un sistema dinámico: !!!def: Sistema Dinámico Un sistema dinámico es una tripleta $(S,T ,\Phi)$, donde $S$ es el espacio de estados (o espacio de fases), $T$ es el espacio de parámetros, y $\Phi: (S \times T ) \to S$ es la evolución.  En el apartado anterior, la regla fija era un mapa o una EDO que sólo definía recursivamente la evolución. En esta definición, $\Phi$ define todo el sistema, mapeando dónde va cada punto de $S$ para cada valor de $T$. Es la forma funcional de la regla fija, que desenreda la recursividad y permite ir de un estado inicial a cualquier estado alcanzable desde él dando un valor al parámetro. En las EDO, $\Phi$ desempeña el papel de la solución general, como una familia de soluciones de un parámetro (literalmente una familia de transformaciones del espacio de fase de un parámetro). En esta solución general, se puede saber, para **cualquier** estado inicial, dónde estará el sistema para **cualquier** valor válido del parámetro, todo en una función de dos variables. !!!ejemplo:Ejemplos 1. En el modelo de crecimiento maltusiano, $x' = kx$, con $k\in\mathbb{R}$, y $x(t) \geq 0$ una población, la solución general viene dada por $x(t) = x_0e^{kt}$, donde $x_0 \in [0,\infty)$ es el valor inicial de la población, cuando $t = 0$. Realmente, el modelo funciona para $x_0\in \mathbb{R}$ pero, si el modelo representa el crecimiento de la población, entonces las poblaciones iniciales no pueden ser negativas, por tanto, $S = [0,\infty)$, $T = \mathbb{R}$ y $\Phi(s,t) = se^{kt}$. 2. Sea $x' = -x^2t$, $x(0) = x_0 > 0$. Por medio de la técnica de separación de variables podemos integrar esta expresión para encontrar la solución general: $x(t) = \frac{1}{\frac{t2}{2}+C}$. Y como $x_0 = \frac{1}{C}$, obtenemos que: $\Phi(x_0,t) = \frac{1}{\frac{t^2}{2} +\frac{1}{x_0}} = \frac{2x_0}{x_0t^2 + 2}$. Aquí, $S = (0,\infty)$, y podemos elegir $T = \mathbb{R}$. En dinámicas discretas, donde tenemos un mapa $f: X\to X$, necesitaríamos una única expresión para poder escribir $\Phi(x,n) = f^n(x)$, algo que no siempre es fácil o factible, ya que implicaría encontrar una forma funcional para una relación recursiva. !!!ejemplo:Ejemplos 1. Sea $f:\mathbb{R}\to \mathbb{R}$ definida por $f(x) = rx$, para $r \geq 0$. Entonces $\Phi(x,n) = r^nx$. 2. Para los conejos de Leonardo de Pisa, tendremos que utilizar la recursión para calcular la población de cada mes y llegar a la marca de 10 años. Sin embargo, si pudiéramos encontrar una forma funcional para la recursión, dando la población en términos de meses, podríamos simplemente introducir $12 \cdot 10 = 120$ meses para calcular la población después de 10 años. Esta última forma funcional es la evolución $\Phi$ en la definición de sistema dinámico anterior. En general, encontrar $\Phi$ (en esencia, resolver el sistema dinámico) es muy difícil, si no imposible, y ciertamente a menudo poco práctico y/o tedioso. Sin embargo, a menudo se da el caso de que el propósito de estudiar un sistema dinámico no es realmente resolverlo. Se trata más bien de comprender la estructura de sus soluciones. En realidad, se trata de hacer afirmaciones cualitativas sobre el sistema más que cuantitativas. Esta idea nos lleva a dar una definición menos rigurosa de los sistemas dinámicos, que a veces se usa en otras disciplinas de un carácter menos matemático: !!!def Los sistemas dinámicos como campo de estudio intentan comprender la estructura de un sistema matemático cambiante identificando y analizando las cosas que no cambian. !!!side:8 En matemáticas, se reserva la palabra **simetría** muchas veces como sinónimo de **invariante**. Hay muchas formas de identificar y clasificar esta noción de una cantidad que no cambia en medio de un sistema cambiante. Pero la idea general es que si una cantidad dentro de un sistema no cambia mientras el sistema en su conjunto evoluciona, entonces esa cantidad tiene un estatus especial como **simetría** [8]. La identificación de las simetrías puede permitirnos localizar e identificar las soluciones de un sistema dinámico. O se puede utilizar una simetría para crear un nuevo sistema, más simple que el anterior, en el que la simetría se ha factorizado, reduciendo el número de variables o el tamaño del sistema. Más concretamente, estas son algunas de las nociones más comunes: * **Invarianza**: A veces, una cantidad, definida como una función en todo o parte del espacio de fase, es constante a lo largo de las trayectorias del sistema. Si se pudiera crear un nuevo sistema de coordenadas del espacio de fase donde una coordenada corresponde a las trayectorias, entonces las curvas solución corresponden a valores constantes de esta coordenada. De esta forma, el nuevo sistema tiene entonces menos grados de libertad que el original. Un caso particular es el del **volumen del espacio de fase** en un campo vectorial conservativo, donde si tomamos una pequeña bola de puntos de un cierto volumen y luego la movemos a lo largo de las trayectorias, la bola de puntos normalmente se doblará y estirará de maneras muy complicadas, pero seguirá siendo un conjunto abierto y de igual volumen. Este hecho se conoce como **conservación del volumen de fase**, y dice mucho sobre el comportamiento y los tipos de curvas solución. * **Periodicidad**: A veces las trayectorias individuales son cerradas, y vuelven sobre sus pasos en ciertos intervalos de tiempo. Si todo el sistema se comporta así, la dirección del flujo contiene información limitada sobre las trayectorias del sistema. En cierto sentido, se puede factorizar la periodicidad, revelando más sobre las direcciones restantes del espacio de estados. O incluso cerca de una solución periódica singular aislada, se puede discretizar el sistema obteniendo un número de variables menor que el original. * **Asintótica**: En ciertas EDOs autónomas, se puede empezar en cualquier momento del tiempo y la evolución depende sólo del tiempo inicial. En este tipo de sistemas, el comportamiento a largo plazo de las soluciones puede ser más importante que la situación en la que se encuentran en un momento concreto del tiempo. En cierto sentido, se estudia el comportamiento asintótico del sistema, en lugar de intentar resolverlo. Las soluciones especiales, como los equilibrios y los ciclos límite, son fáciles de encontrar, y sus propiedades se convierten en elementos importantes del análisis. # Caos Como ejemplo de la complejidad que se esconde detrás del estudio general de sistemas dinámicos vamos a ver cómo analizar el comportamiento asintótico de las trayectorias, intentando describir su comportamiento en forma de convergencia a un punto fijo o periodicidad. !!!side:9 Es decir, las trayectorias que comienzan en $A$ no salen de $A$. !!!def: Atractores Un **atractor** de un sistema dinámico $(S,T ,\Phi)$ es un subconjunto de $A\subseteq S$ tal que: 1. $A$ es **invariante**: $\Phi(A,t)\subseteq A$, para todo $t\in T$ [9]. 2. $A$ **atrae** un conjunto abierto de condiciones iniciales, $U$: existe un abierto, $U$, tal que si $x(0)\in U$, entonces $x(t)$ se acerca a $A$ con el tiempo. Al mayor abierto, $U$, verificando esta propiedad, se le llama **cuenca de atracción**. 3. $A$ is **minimal**: no tiene ningún subconjunto propio verificando las condiciones anteriores. Un **punto fijo** es un punto verificando: $\Phi(x,t)=x$, para todo $t\in T$. Como hemos comentado anteriormente, el estudio de la periodicidad, invariantes y comportamiento asintótico nos puede dar mucha información acerca del sistema dinámico incluso aunque no seamos capaces de resolverlo completamente (que será la mayoría de las veces). En el caso particular de estar trabajando con sistemas dinámicos continuos unidimensionales que provienen de EDO's las cosas son fáciles y tenemos, esencialmente, dos opciones: !!!side:10 Un **repulsor** es lo contrario de un atractor: las órbitas de los puntos que empiezan cerca de él tienden a alejarse (es decir, llega un momento que no están nunca más cerca de un entorno del repulsor). !!!teorema: Teorema Si el sistema dinámico proviene de un EDO unidimensional, entonces los puntos fijos son atractores o repulsores [10], no hay más opciones.  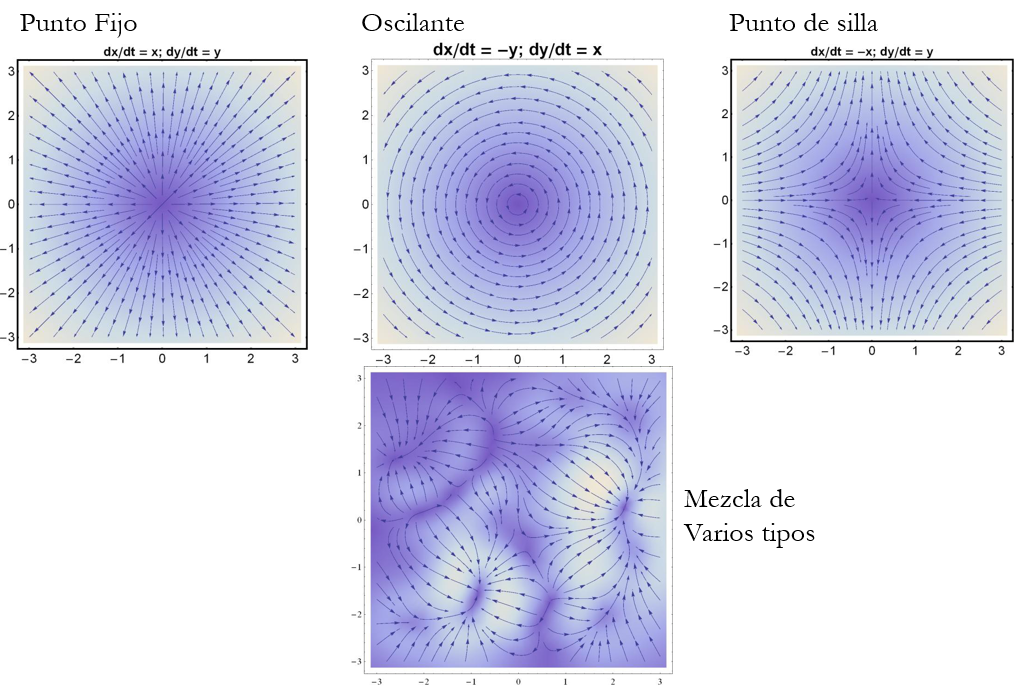Cuando subimos a 2 dimensiones, la cosa se complica un poco, pero todavía hay una clasificación comprensible: !!!side:11 La figura siguiente muestra la posible combinación de casuísticas que podemos encontrarnos en 2D:  !!!teorema: Teorema de Poincare-Bendixon En el plano, solo se presentan puntos fijos u órbitas cerradas [11]. Sin embargo, en dimensiones superiores se observan comportamientos caóticos, y los atractores no son ni puntos, ni curvas simples, ni áreas simples, y pasan a llamarse **atractores extraños** (muchas veces tienen estructura fractal).  Y entonces hemos de precisar qué entendemos por un comportamiento caótico: !!!side:12 Los sistemas que verifican el determinismo fuerte son *sencillos*. Los que verifican únicamente el determinismo débil, a pesar de ser deterministas, pueden llegar a ser *impredecibles*, y los asociamos habitualmente a un comportamiento caótico.  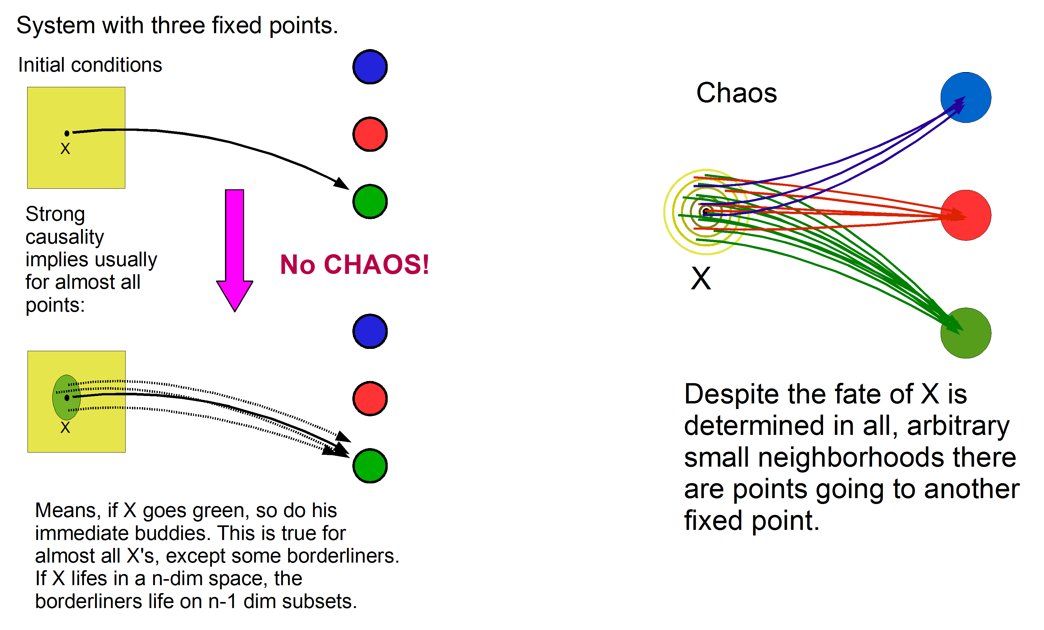!!!def: Determinismo [12] Si suponemos un sistema dinámico prefijado, podemos definir dos tipos de comportamientos deterministas: * **Determinismo Débil**: si condiciones iniciales idénticas conllevan trayectorias idénticas. * **Determinismo Fuerte**: si, además de verificar las condiciones del Determinismo Débil, se tiene que condiciones iniciales *similares* conllevan órbitas cercanas. !!!ejemplo:Ejemplo: La curva de Lorenz E. Lorenz creó un modelo para ciertos fenómenos meteorológicos, donde observó una dependencia crítica de las condiciones iniciales, lo que constituyó la primera observación *real* de determinismo débil. Una de las características que observó fue que, a pesar de ser un sistema determinista, pequeñas variaciones en el estado inicial provocaban grandes diferencias en el comportamiento asintótico de las trayectorias, lo que quería decir que no había una relación lineal entre la precisión y el tiempo.  Pero con el tiempo se ha visto que es un comportamiento habitual en la mayoría de los sistemas dinámicos multidimensionales:  # Primeras conclusiones Los sistemas dinámicos, como campo de estudio, son un tipo de análisis matemático: el estudio de las propiedades formales de conjuntos de objetos y de las estructuras definidas sobre ellos (en forma de funciones, espacios, etc.). Sin embargo, el análisis se centra en los aspectos más técnicos del cálculo y la determinación de las propiedades de las funciones definidas sobre un conjunto particular, la recta real $\mathbb{R}$. De hecho, las propiedades de las funciones y los espacios que sirven como sus dominios (y codominios) están íntimamente entrelazados de maneras a veces obvias y a menudo sutiles. Por ejemplo, según un célebre teorema de Luitzen E. J. Brouwer [1912]: !!!teorema: Teorema de Brouwer Toda función continua de un espacio compacto y convexo en sí mismo debe contener al menos un punto fijo. Esta propiedad tiene enormes implicaciones no sólo para la función que aplicamos al espacio, sino para el propio espacio. Las consecuencias de un teorema como éste son evidentes incluso en las etapas iniciales de las matemáticas, como el cálculo y las ecuaciones diferenciales. En general, estudiar cómo se mueve un mapa alrededor de los puntos del espacio es estudiar el contenido dinámico del mapa. A dónde van los puntos, tras la iteración repetida de un mapa sobre un espacio, o cómo se comportan las soluciones de una ecuación diferencial una vez conocido su dominio de parámetros, es estudiar el sistema dinámicamente. Si la mayoría o todas las soluciones tienden a parecerse, o si la diversidad de formas de una colección de iteraciones de un punto bajo un mapa es pequeña, entonces decimos que la dinámica es simple. En esencia, son fáciles de describir, o no hace falta mucha información para describirlas. Por el contrario, si las diferentes soluciones de la EDO pueden hacer muchas cosas diferentes, o si se necesita mucha información para describir las diferentes formas en que un mapa puede mover distintos puntos en un espacio, decimos que la dinámica es compleja o complicada. Se puede decir que un sistema dinámico es más interesante si es más complicado de describir, aunque ciertamente es un término subjetivo. Resolver un sistema dinámico, o encontrar una expresión explícita para la evolución, no suele ser el objetivo general del análisis de los sistemas dinámicos. Muchos sistemas no lineales de EDO son difíciles, si no imposibles, de resolver. Por ello, el objetivo del análisis de un sistema dinámico es la descripción general del movimiento de los estados bajo el mapa o la EDO. En vista de ello, podemos definir informalmente los sistemas dinámicos teniendo en cuenta estas consideraciones: !!!def Los sistemas dinámicos son el estudio de la información contenida en los grupos de transformaciones de un espacio y de sus efectos. Para un sistema dinámico discreto definido por un mapa sobre un espacio, las propiedades del mapa, así como las del espacio, afectarán a cómo se mueven los puntos en el espacio. Los mapas con ciertas propiedades sólo pueden hacer ciertas cosas, y si el espacio tiene una propiedad particular, como ser compacto y/o convexo, entonces ciertas cosas deben ser ciertas (o pueden no serlo), como una transformación libre de punto fijo. La dinámica es la exploración de estas ideas. (insert menu.md.html here)