**IAIC**
Búsquedas Ciegas e Informadas
!!!warn:
La implementación desarrollada en este tema se puede descargar [aquí](./modelos/BCI.nlogo).
# Estructuras en Espacios de Estados
Hemos visto que para representar un problema como una búsqueda en un Espacio de Estados necesitamos los siguientes elementos:
1. Conjunto de Estados: $X$
1. Estado inicial: $s_0\in X$
1. Estados finales: $G\subseteq X$
1. Función de transición (acciones): $T:X\to \cal{P}(X)$
Las transiciones aportan una **estructura interna** al espacio completo de estados, $X$, que lo convierte en un espacio conectado, donde tiene sentido plantearse si hay caminos que conecten $s_0$ con $G$ y, en caso afirmativo, intentar construir el camino más *deseable* (óptimo, desde algún punto de vista). Aunque a veces $T$ viene dado con el problema, muchas veces determinar el par $(X,T)$ es parte de la **representación del problema**.
En cierta forma, el par $(X,T)$ se comportaría como un **espacio topológico**, en donde las conexiones entre estados por medio de transiciones están definiendo una relación de conectividad que configura el espacio de una cierta forma: si cambiamos las transiciones disponibles, la forma del espacio cambia. Como hemos comentado, la elección adecuada de $X$ y de $T$ puede modificar sensiblemente la resolubilidad del problema original.
!!!note: Problemas representables
El tipo de problemas que se puede resolver con esta representación es variado, dependiendo de los requerimientos adicionales (no excluyentes entre sí) que consideremos para dar una solución:
* Si solo indicamos si existe un camino, pero no especificamos cuál, estamos resolviendo un **problema de decisión**.
* Si $G$ viene dado por un conjunto de propiedades que deben verificarse en los estados alcanzados, entonces el problema se podría ver como un **problema de satisfacción de restricciones**.
* Si, además, proporcionamos un estado de $G$ al que podemos llegar desde $s_0$, estamos resolviendo un **problema de construcción**.
* Si, por encima de las dos anteriores, además estamos dando el conjunto de transiciones/acciones que llevarían desde $s_0$ a un elemento de $G$, estamos resolviendo un **problema de planificación**.
* Si en cualquiera de los problemas anteriores preferimos dar uno de los caminos o estados finales que verifique propiedades adicionales de optimalidad, entonces al problema de búsqueda le añadimos un **problema de optimización**.
## Construcción de $T^n(s_0)\subseteq X$
Lo más habitual es no disponer de $X$ de forma explícita y completa al principio de la búsqueda, sino que hemos de ir construyéndolo/descubriéndolo a partir de $s_0$ por aplicación sucesiva de elementos de $T$. Grosso modo, cuando $T$ se puede expresar como un conjunto finito de aplicaciones, $T=\{t_1,\dots,t_n\}$, esta construcción la podemos ver como un proceso iterativo en el que, partiendo de $s_0$, construimos por niveles los estados que podemos alcanzar por aplicación de los elementos de $T$:
$$\{s_0\}$$
$$\{s_1=t_1(s_0),\dots,s_n=t_n(s_0)\}$$
$$\{s_{11}=t_1(s_1),\dots,s_{1n}=t_n(s_1),\dots,s_{n1}=t_1(s_n),\dots,t_{nn}=t_n(s_n)\}$$
$$\vdots$$
En general, para cualesquiera $\{i_1, \dots, i_k, i_{k+1}\}\subseteq \{1,\dots,n\}$ podríamos considerar:
$$s_{i_1\dots i_k i_{k+1}}=t_{i_{k+1}}(s_{i_1\dots i_k})=t_{i_{k+1}}\circ \cdots \circ t_{i_1}(s_0)$$
donde $f\circ g$ representa la composición de aplicaciones: $f\circ g(x)=f(g(x))$.
Si el espacio $(X,T)$ es fuertemente conexo (es decir, desde cualquier estado puedo conseguir cualquier otro por aplicación sucesiva de elementos de $T$), entonces el problema de búsqueda tendrá solución, independientemente de $s_0$ y $G$, es decir, que sabemos que hay, al menos, una sucesión de transiciones que lleva desde $s_0$ hasta una solución. Muchas veces la situación no es esa, y entonces dependerá de $T$ para que, al menos, podamos alcanzar algún elemento de $G$ desde un $s_0$ concreto.
Además, en caso de que sí sea alcanzable, puede haber más de un camino que lleve a un estado final, pudiendo variar de un camino a otro en el orden de aplicación de las transiciones que se han aplicado, en la longitud de la cadena de transiciones aplicadas, o en las propiedades que verifiquen las transiciones elegidas (por ejemplo, si son conmutativas, $t_i\circ t_j=t_j\circ t_i$, asociativas, $t_i\circ (t_j\circ t_k)=(t_i\circ t_j)\circ t_k$, etc.), entre otras muchas. Conocer a priori las propiedades que verifica $T$ puede simplificar la generación de los estados de $X$, ya que puede evitar la creación de estados repetidos innecesariamente o de caminos esencialmente equivalentes (o de caminos indeseables).
Partiendo de esta visión iterada de cómo construir elementos de $X$, podemos dar las funciones necesarias para hacerlo de forma compacta en un lenguaje como NetLogo (aunque lo que hagamos aquí se puede aplicar de forma directa en muchísimos otros lenguajes de programación).
# Una implementación sencilla
Vamos a suponer que tenemos $T$ en forma de colección (lista, en el caso de NetLogo, pero donde el orden de aparición no jugará ningún papel) de funciones anónimas:
$$T=\{t_1,\dots,t_n\}=[t_1,\dots,t_n]$$
donde cada $t_i:X\to X$.
!!!note
En general, el conjunto de reglas aplicables depende del estado concreto en el que nos encontremos, pero para simplificar la notación, y porque muchas veces ocurre así, podemos considerar que en todos los estados las reglas a aplicar son las mismas. Si no fuese este el caso, debemos calcular para cada estado $s$ el conjunto $T_s$ de transiciones aplicables.
Vamos a hacer uso de la función `map`, que recordemos que hace lo siguiente:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
map f [a1 ... an] = [f(a1) ... f(an)]
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
es decir, aplica una función determinada a todos los elementos de una lista.
Como nosotros queremos aplicar una lista de funciones a un elemento fijo, podemos aprovechar esta estructura para hacerlo eligiendo adecuadamente qué función `f` aplicar. Si `Tr` es la lista que contiene las transiciones, entonces, para conseguir todos los estados alcanzables desde s basta hacer:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
map [t -> (run-result t s)] Tr
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Para empaquetar este proceso como una función podemos definir:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
to-report children-state [s]
report (map [t -> (run-result t s)] Tr)
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Si disponemos de un predicado, `final?`, que indica cuándo un estado es final o no, podemos reproducir la construcción a partir de $s_0$ hasta un estado final como:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
to-report Generate-X-from [s0]
let Fr (list s0)
let X Fr
while [empty? filter final? Fr]
[
set Fr reduce sentence (map children-state Fr)
set X sentence X Fr
]
report X
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Vemos que la generación de $X$ (hasta que encontremos algún elemento de $G$) es realmente directa gracias a la aproximación funcional:
1. Partiendo de la frontera inicial: $Fr=\{s_0\}$.
2. Construimos los sucesores de $Fr$ por la aplicación de todas las transiciones disponibles a todos los elementos de la frontera.
3. Acumulamos $Fr$ en $X$ (para no perder los estados obtenidos).
4. Si en $Fr$ no hay elementos de $G$, repetimos desde el paso 2. En caso contrario, devolvemos $X$.
Trabajar con la frontera ayuda a no estar calculando continuamente los sucesores de estados por los que ya hemos pasado en etapas anteriores (esto no asegura no tener repetidos, pero al menos no repite el mismo proceso una y otra vez sobre todos los elementos).
Observa que no solo se ha usado `map`, sino que también se ha hecho uso de `reduce`: la aplicación de `map` sobre cada estado devuelve una lista de estados, por lo que la aplicación sobre la frontera resulta en una lista de listas, aplicar una reducción con `sentence` permite unir todas las listas en una sola.
Aunque así se ha simplificado mucho el proceso, se deja fuera una parte que es esencial pero que se puede introducir sencillamente gracias a la programación funcional: aunque se tenga una representación uniforme de los estados de $X$, es probable que haya elementos representables que no se correspondan con estados válidos (por ejemplo, una representación de estados como números, pero donde solo tengan sentido los números positivos). Para tener en cuenta estas limitaciones, es posible tomar dos estrategias:
1. **Restringir $T$**: Las transiciones de $T$ solo generan estados válidos.
2. **Validar $T$**: Tras generar posibles estados por elementos de $T$, se desechan aquellos que no son válidos.
Cuando las características de los estados están claras, la implementación de la segunda estrategia es directa (apenas un pequeño cambio) y facilita la construcción de $T$ desde el punto de vista de la programación. Para ello, supondremos que existe un predicado, `valid?`, que indica si un estado es válido o no (o, mejor dicho, si una representación realmente es un estado). Con este predicado, y la función de orden superior, `filter`, basta cambiar la función que calcula los sucesores de la siguiente forma:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
to-report children-state [s]
report filter valid? (map [t -> (run-result t s)] Tr)
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
No es necesario cambiar nada de los demás procedimientos, porque la generación de sucesores se ha restringido para devolver solo estados válidos.
Sin embargo, todavía se puede mejorar el proceso de generación eliminando los estados repetidos:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
to-report Generate-X-from [s0]
let Fr (list s0)
let X Fr
while [empty? filter final? Fr]
[
set Fr reduce sentence (map children-state Fr)
set Fr remove-duplicates filter [s -> not member? s X] Fr
set X sentence X Fr
]
report X
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Generación Selectiva
Desde un punto de vista computacional, la generación anterior tiene muchas deficiencias. Aunque va generando todos los estados de $X$ que se pueden obtener a partir de $s_0$, no es un mecanismo que se pueda ofrecer como solución a problemas de búsqueda porque tiene muchas opciones de explotar exponencialmente (tanto en memoria, es decir, número de estados que van apareciendo, como en tiempo, por el número de aplicaciones de $T$ que se aplican en cada paso) en cuanto la media de transiciones aplicables desde cada estado sea mayor que $1$. Además, muchísimos de los estados generados en el proceso no tendrán ningún valor para la solución de la búsqueda.
Por ello, los algoritmos de búsqueda implementan **estrategias** que permiten recorrer/generar $X$ haciendo la expansión de un solo estado en cada paso, con el fin de controlar la complejidad del proceso de generación e intentar introducir algo de *inteligencia* en el proceso de selección.
La forma general de un proceso de búsqueda que usa **selección de estados** para expandir $X$ se puede obtener muy fácilmente a partir del algoritmo anterior:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
to-report Selected-Search-from [s0]
let Fr (list s0)
let X Fr
while [empty? filter final? Fr]
[
let sel-s select Fr
set Fr sentence (children-state sel-s) (remove sel-s Fr)
set Fr remove-duplicates Fr
set X remove-duplicates sentence X Fr
]
report X
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
donde `select` sería la estrategia: una función que selecciona, de entre los estados de la frontera que podemos expandir, el estado concreto que vamos a expandir en este paso.
Si, por ejemplo, se toma:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
to-report select [C]
report one-of C
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
el resultado será una **búsqueda aleatoria** (`one-of` devuelve un elemento al azar de una lista).
## Búsqueda Ciega: Generación sin información
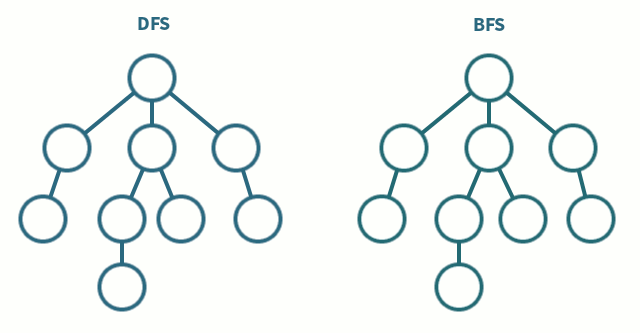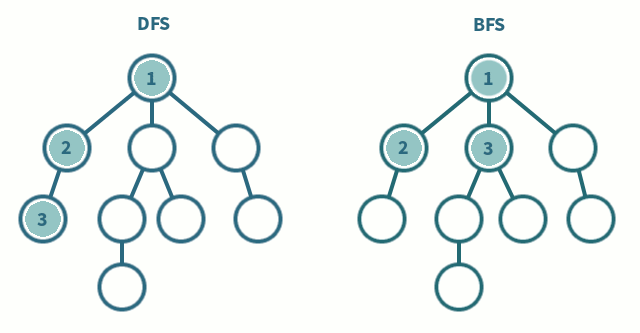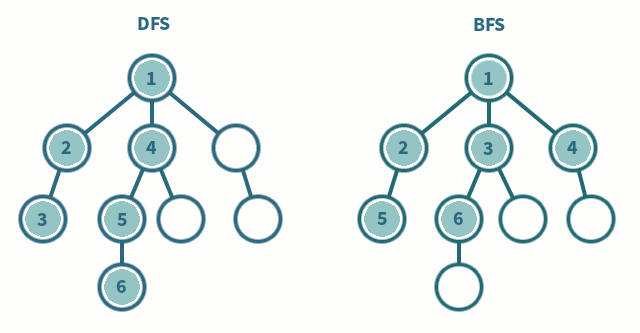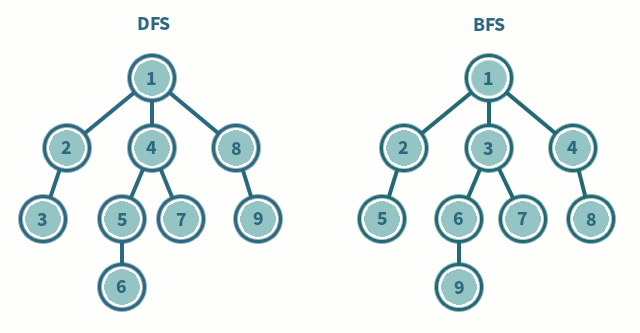
Si `Tr` es una lista ordenada, su orden induce un orden de aparición de los estados durante la generación de $X$. Si no se dispone de información acerca de cómo construir una estrategia que acelere el proceso de búsqueda (lo que se denomina una **búsqueda ciega**) se podría usar el orden impuesto por `Tr` para recorrer $X$ de manera ordenada.
Por ejemplo, para seguir ordenadamente cada nivel de la estructura de $X$ que se genera desde $s_0$, bastaría con ir seleccionando de la frontera el primer estado disponible y añadir los estados que se generan desde él a la cola de la frontera (en programación, es lo mismo que usar una estructura de tipo FIFO), y entonces la búsqueda se conoce como **búsqueda en anchura** (BFS, por sus siglas en inglés). Concretamente, la selección usada sería:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
to-report BFS-from [s0]
let Fr (list s0)
let X Fr
while [empty? filter final? Fr]
[
let sel-s selectBFS Fr
set Fr sentence (bf Fr) (children-state sel-s)
set Fr remove-duplicates Fr
set X remove-duplicates sentence X Fr
]
report X
end
to-report selectBFS [C]
report first C
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Si se quiere que la **búsqueda sea en profundidad** (DFS, por sus siglas en inglés) se puede seguir seleccionando el primer estado de la frontera, pero ahora se añaden los estados que se generan desde él a la cabeza de la frontera (se construye una estructura de tipo FILO):
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
to-report DFS-from [s0]
let Fr (list s0)
let X Fr
while [empty? filter final? Fr]
[
let sel-s selectDFS Fr
set Fr sentence (children-state sel-s) (bf Fr)
set Fr remove-duplicates Fr
set X remove-duplicates sentence X Fr
]
report X
end
to-report selectDFS [C]
report first C
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
## Búsqueda Informada: Generación con información
Si la estrategia de selección es muy eficiente, la búsqueda será más rápida porque no generará una sección muy grande de $X$ para poder resolver el problema.
Normalmente, la dificultad al resolver un problema de búsqueda no se encuentra en verificar las condiciones de $G$ ni en la aplicación de los elementos de $T$, sino en la cantidad de estados adicionales que hay que generar para poder encontrar una solución, así que es normal que muchos de los esfuerzos en la resolución de problemas de búsqueda vayan orientados a reconocer propiedades adicionales de la estructura de $X$ que sirvan para definir estrategias más eficientes. Los algoritmos de búsqueda que usan este tipo de estrategias se dice que realizan una **búsqueda informada**, y uno de sus representantes más claros es el **algoritmo $A^∗$**, en el que la estrategia de búsqueda intenta minimizar el coste del camino recorrido:
!!!def
Cuando la aplicación de cada transición lleva aparejado un coste, o lo que es lo mismo, la estructura $(X,T)$ se puede representar como un grafo ponderado, en el que la transición que lleva $s$ a $s′$ se representa como una arista dirigida $(s\to s′)$ con un peso predeterminado y conocido, el algoritmo $A^∗$ calcula el camino de menor peso entre $s_0$ y un elemento de $G$ considerando que la estrategia en cada paso selecciona el nodo de la frontera que minimiza:
$$g(s)=coste(s)+h^∗(s)$$
donde $coste(s)$ es el coste real del camino que se ha construido desde $s_0$ hasta $s$, y $h^∗(s)$ es una estimación del coste mínimo que habría desde $s$ hasta $G$.
$h^∗$ se conoce como **función heurística**, y suele ser desconocida, por lo que se usan aproximaciones que podemos calcular (que denotaremos por $h$). Para asegurar que esta estrategia realmente devuelve el camino de coste mínimo usando estas aproximaciones, éstas deben verificar algunas propiedades adicionales.
En código:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
to-report select-A* [C]
let s* min-of-in [s -> (coste s) + (h s)] C
report s*
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
donde `(min-of-in f C)` devuelve el elemento de `C` donde `f` alcanza el menor valor de `C`.

### Condiciones para la optimalidad
Hasta ahora no hemos hablado de cómo garantizar la optimalidad de la solución. Es claro que, en el caso degenerado ($h=0$), tenemos una búsqueda en anchura guiada por el coste del camino explorado, lo que garantiza el óptimo aunque a costa de un mayor tiempo de búsqueda. Pero, como hemos comentado, la función $h$ permite introducir un comportamiento de búsqueda en profundidad, donde sabemos que no se garantiza el óptimo, pero a cambio podemos realizar la búsqueda en menor tiempo porque podemos evitar explorar ciertos caminos.
Para saber si encontraremos o no el óptimo mediante el algoritmo $A^∗$ hemos de analizar las propiedades de la función heurística.
La propiedad clave que garantizará hallar la solución óptima es la que denominaremos **admisibilidad**:
!!!def: Admisibilidad
Diremos que una función heurística $h$ es **admisible** cuando su valor en cada nodo sea menor o igual que el valor del coste real del camino que falta por recorrer hasta una solución, es decir:
$$\forall n\ (0\leq h(n)\leq h^∗(n))$$
Esto quiere decir que la función heurística ha de ser un **estimador optimista** del coste que falta para llegar a una solución. Esta propiedad implica que, si podemos demostrar que la función de estimación $h$ que utilizamos en nuestro problema la cumple, siempre encontraremos una solución óptima. El problema radica en hacer esa demostración, pues cada problema es diferente.
La **consistencia** se puede ver como una extensión de la admisibilidad. A partir de la admisibilidad se deduce que si tenemos los costes heurísticos $h^∗(n_i)$ y $h^∗(n_j)$, y el coste óptimo para ir de $n_i$ a $n_j$, $K(n_i,n_j)$, se ha de cumplir la desigualdad triangular:
$$h^∗(n_i)\leq h^∗(n_j)+K(n_i,n_j)\quad (\mbox{o, equivalentemente, }h^∗(n_i)- h^∗(n_j)\leq K(n_i,n_j))$$
La consistencia exige pedir lo mismo al estimador $h$.
!!!def:Consistencia
Un heurístico $h$ se dice **consistente** si para cualquier par de nodos $n_i$, $n_j$ verifica que:
$$h(n_i)−h(n_j)\leq K(n_i,n_j)$$
Es decir, que la diferencia de las estimaciones sea menor o igual que la distancia óptima entre nodos. Que esta propiedad se cumpla quiere decir que $h$ es un **estimador uniforme** de $h^∗$. Es decir, la estimación de la distancia que calcula $h$ disminuye de manera uniforme.
Si $h$ es consistente además se cumple que el valor de $g(n)$ para cualquier nodo es $g^∗(n)$ (es decir, el mínimo), por lo tanto, una vez hemos llegado a un nodo sabemos que hemos llegado a él por el camino óptimo desde el nodo inicial. Si esto es así, no es posible encontrar el mismo nodo por un camino alternativo con un coste menor y esto hace que el tratamiento de nodos cerrados duplicados sea innecesario, lo que ahorra tener que almacenarlos.
Suele ser un resultado habitual que las funciones heurísticas admisibles sean consistentes y, de hecho, hay que esforzarse bastante para conseguir que no sea así.
Otra propiedad interesante es la que permite comparar heurísticas entre sí, y poder saber cuál hará que $A^∗$ necesite explorar más nodos para encontrar una solución óptima:
!!!def:Heurísticos más informados
Se dice que el heurístico $h_1$ es **más informado** que el heurístico $h_2$ si se cumple la propiedad:
$$\forall n\ (0\leq h_2(n) < h_1(n)\leq h^∗(n))$$
En particular, poder verificar esta propiedad implica que los dos heurísticos son admisibles.
Si un heurístico es más informado que otro, al hacer uso de él en el algoritmo $A^∗$ se expandirán menos nodos durante la búsqueda, ya que su comportamiento será más en profundidad y habrá ciertos nodos que no se explorarán.
!!!Tip
Esto podría hacer pensar que siempre hay que escoger el heurístico más informado, pero se ha de tener en cuenta que la función heurística también tiene un tiempo de cálculo que afecta al tiempo de cada iteración, y que suele ser más costoso cuanto más informado sea el heurístico. Podemos imaginar por ejemplo que, si tenemos un heurístico que necesita $10$ iteraciones para llegar a la solución, pero tiene un coste de 100 unidades de tiempo por iteración, tardará más en llegar a la solución que otro heurístico que necesite $100$ iteraciones pero que solo necesite una unidad de tiempo por iteración. Lo que lleva a buscar un equilibrio entre el coste del cálculo de la función heurística y el número de expansiones que ahorramos al utilizarla. En este sentido, es posible que una función heurística peor acabe dando mejor resultado.
De todo lo anterior deducimos que la heurística controla el comportamiento de $A^*$. Concretamente:
* En un extremo tenemos el caso en el que $h(n)=0$ siempre. Entonces, solo $coste(n)$ jugará algún papel en el algoritmo, y $A^*$ se convierte en el **algoritmo de Dijkstra**, que garantiza encontrar el camino mínimo.
* Si $h(n)\leq h^∗(n)$ entonces se garantiza que $A^*$ encontrará el camino más corto. Cuanto menor sea $h(n)$ más nodos tendrá que expandir $A^*$ y su ejecución será más lenta.
* Si $h(n)=h^∗(n)$, entonces $A^*$ solo seguirá caminos óptimos, y será más rápido (pero puede seguir expandiendo muchos nodos si hay muchos caminos mínimos de igual longitud). Aunque en general será difícil estar en el caso de una $h$ perfecta, es interesante saber que con información perfecta, $A^*$ se comporta perfectamente.
* Si $h(n)$ no es admisible, es decir, a veces es mayor que $h^∗(n)$, entonces $A^*$ no garantiza encontrar el camino mínimo, pero puede encontrar un camino al objetivo muy rápido.
* Por último, si $h(n)$ es muy grande en relación con $coste(n)$, entonces solo $h(n)$ tendrá alguna influencia sobre $A^*$, convirtiendo el algoritmo en un **Algoritmo Voraz**.
En el caso en que haya muchos caminos óptimos (por ejemplo, cuando estamos trabajando con un problema en el que hay muchos estados que tienen un coste similar), $A^*$ tendrá que ir abriendo muchos nodos para encontrar finalmente alguno de esos caminos. Si queremos acelerar la búsqueda en esos casos habrá que modificar la heurística para romper los **empates** (en la literatura esta técnica se llama *tie-breaking*). Por supuesto, en general la forma de hacerlo dependerá del problema concreto, pero también hay aproximaciones generales como, por ejemplo, de todos los nodos que tienen valor actual de $g$ mínimo seleccionar aquellos que tienen $h$ mínimo (seleccionando primero aquellos hijos que están más cerca del objetivo), o aquellos que tienen $coste$ mínimo (los hijos que están más cerca del inicio). Lo importante es dar algún procedimiento por el cual $A^*$ pueda mantener el orden de selección de los hijos, de forma que explote siempre el mismo camino y así no se pierda en abrir muchos caminos que sean similares, por lo que otra opción es usar una lista ordenada donde se van almacenando los nodos más prometedores, y se selecciona siguiendo este orden (algo parecido a lo que se hace en una búsqueda DFS). Cuando se trabaja con búsquedas en terrenos (algo muy común en aplicaciones de $A^*$ a juegos y navegación) se suele usar una heurística que modifica ligeramente las distancias calculadas (con Manhattan, máximo, euclídea, etc.) para romper los empates.
A veces, como en el caso de los juegos, puede ser interesante tener caminos que no sean óptimos, pero sí se obtengan rápidamente y sean suficientemente buenos, por lo que jugar con las ideas anteriores puede dar resultados deseables aunque dejemos de trabajar con heurísticas admisibles. Por ejemplo, cuando usamos $A^*$ para generar soluciones finales a partir de propiedades (es decir, que no conocemos exactamente el estado asociado, sino algunas restricciones que debe cumplir), y no nos interesa tanto el camino como el ser capaces de llegar.
# Planificación: estados con memoria
Las secciones anteriores consiguen generar estados de $X$, pero no mantienen información acerca de qué transiciones han permitido llegar desde un estado a otro. Esto significa que se ha generado $X$, el espacio de estados (al menos, los estados alcanzables desde $s_0$), pero no hemos mantenido información acerca de $(X,T)$, es decir, la estructura interna que las transiciones proporcionan al espacio de estados. En este sentido, los métodos anteriores pueden resolver problemas de decisión, e incluso problemas de construcción de soluciones, pero no problemas de planificación.
Para generar $(X,T)$ se debe almacenar información acerca de qué transiciones son las que permiten llegar desde un estado a otro. La estructura natural que permite almacenar esta información sería la de un grafo dirigido, y así está definido en la librería de IA oficial del curso (haciendo uso de sistemas multiagente), pero aquí, por motivos educativos solo se mostrarán implementaciones directas.
Para ello, se usará una estructura más rica para los estados manteniendo la información de:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
s = (valor, valor-padre, transicion)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
donde:
* `valor`: es el valor que se almacena en el estado (lo que antes almacenábamos como estado completo), y que representa una posible solución al problema.
* `valor-padre`: es el valor del estado que ha generado a `s` (el antecedente en la construcción). Servirá para poder reconstruir el camino completo para llegar a él.
* `transicion`: es la transición que ha permitido obtener `valor` desde `valor-padre`.
Se puede usar cualquiera de las estructuras de datos habituales en los lenguajes de programación (tablas/diccionarios, structs, arrays,...) para mantener esta información. NetLogo proporciona una estructura muy distinta, permitiendo combinar agentes normales (*turtles*, que pueden mantener los elementos de $X$) junto con agentes relacionales (*links*, que pueden mantener los elementos de $T$).
Para que sea *independiente* de la estructura usada, es más fácil considerar los siguientes constructores y accesos a la información de los estados:
* `(new-state v f t)` genera un estado con valor `v`, padre `f`, y transición `t`.
* `(value-of s)` devuelve el valor del estado `s`.
* `(father-of s)` devuelve el padre del estado `s`.
* `(transition-of s)` devuelve la transición que ha generado el estado `s`.
A partir de estos elementos se modifica adecuadamente el generador de descendientes de un estado como:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
to-report children-state [s]
let v value-of s
report filter valid? (map [t -> (new-state (run-result t v) v t) ] Tr)
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
De donde es fácil construir la modificación del generador para almacenar (y considerar) los nuevos tipos de estados:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
to-report Generate-XT-from [s0]
let Fr (list (new-state s0 s0 "-"))
let XT []
while [empty? filter final? Fr]
[
set XT sentence XT Fr
set Fr reduce sentence (map children-state Fr)
set Fr filter [s -> not member? (value-of s) (map value-of XT)] Fr
]
set XT sentence XT (filter final? Fr)
report XT
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
El resto de variantes vistas anteriormente se adaptan de forma similar.
Por último, el hecho de haber generado el espacio de estados estructurado, $(X,T)$, permite responder al problema de planificación (y, con el algoritmo adecuado, de optimización) devolviendo un camino que conecta el estado inicial con un estado final. Gracias a la información acumulada en los estados, se puede reconstruir el camino de forma regresiva, yendo desde el objetivo/solución alcanzado hasta el estado inicial por medio de las transiciones aplicadas (que se han almacenado para ese fin):
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
to-report path-from [start goal XT]
if start = goal [report (list new-state start start "-")]
let s-g state-with-value goal XT
let f-g father-of s-g
report lput s-g (path-from start f-g XT)
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
donde `start` y `goal` son los valores de los estados inicial y final, respectivamente, y `(state-with-value v XT)` es una función que devuelve el estado (la estructura) de `XT` que tiene valor `v`.
Para usarlo como respuesta de una búsqueda, basta añadir las líneas que devuelven el camino encontrado:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
let g value-of one-of (filter final? XT)
report path-from s0 g XT
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~