**IAIC** Búsquedas Locales y Estocásticas # Búsquedas Locales Hasta ahora hemos visto métodos de resolución de problemas en los que el objetivo ha sido buscar un camino en un espacio de estados (ya sea porque estamos interesados en cómo alcanzar un estado final, o porque es el propio camino el que nos interesa), pero podemos encontrarnos que no siempre es factible esta aproximación, algo que puede ocurrir por dos razones principalmente: * Porque este planteamiento resulte **demasiado artificial** y lejano al problema porque **no haya operadores de transición**, o porque no sea natural asociar una función de coste a dichos estados, o * Porque no hay posibilidad de hallar una solución óptima debido a que el **tamaño del espacio de búsqueda es demasiado grande**, y en este caso nos conformamos con una solución que podamos considerar **suficientemente** buena. !!!note Aunque antes hemos indicado que es normal añadir la restricción de que el Espacio de Estados sea finito, algo conveniente para los métodos vistos en el tema anterior, ahora no es estrictamente necesario, y los métodos locales que veremos aquí también se pueden aplicar en casos en los que el Espacio de Estados es infinito, incluso no numerable. Si estamos ante un caso así, podemos encontrarnos con dos opciones: 1. Si es relativamente asequible encontrar una solución inicial, aunque no sea demasiado buena, podemos cambiar nuestra tarea de buscar un camino entre estados a **encontrar una mejora sucesiva** en el espacio de soluciones. 2. Si no es posible encontrar una solución inicial (aunque no sea suficientemente buena) podemos ver si, partiendo de una solución no válida, podemos ir construyendo una solución que sí lo sea. En este cambio de perspectiva, pues, lo que suponemos es que podemos navegar dentro del espacio de las posibles soluciones, realizando operaciones sobre ellas que pueden ayudar a mejorarlas. Estas operaciones no tienen porqué tener una representación en el mundo real, sino que son simplemente formas de manipular las posibles soluciones para encontrar otras opciones. El coste de estas operaciones no será tan relevante ya que lo que estamos buscando es la calidad de las soluciones, y no la forma de llegar a ellas. Al igual que en las estrategias vistas en temas anteriores disponíamos de una función de coste que indicaba lo bueno que podía ser el camino que hacía uso de esas operaciones, ahora necesitamos una función que, según algún criterio (dependiente del dominio), medirá su calidad y permitirá ordenarlas respecto a lo buenas que sean. La estructura general que tendremos en este tipo de aproximaciones es similar al que destacamos en las búsquedas en estados de espacios: 1. Una **solución inicial**, que en este caso será una solución completa, no un trozo inicial del camino y que, aunque la llamemos así, no tiene porqué ser una solución en su sentido estricto. 2. **Operadores de transformación de la solución**, que en este caso manipularán soluciones completas y que no tendrán un coste asociado. 3. Una **función de calidad**, que debe medir lo buena que es una solución y permitirá dirigir la búsqueda. A diferencia de las funciones heurísticas anteriores, en este caso esta función no indica cuánto falta para encontrar la solución que buscamos, sino que proporciona una forma de comparar la calidad entre soluciones para indicarnos cuál es la dirección que debemos tomar para encontrar soluciones mejores. Debido a que puede no ser posible encontrar la mejor solución, saber cuándo hemos acabado la búsqueda dependerá totalmente del tipo de algoritmo que diseñemos, que tendrá que decidir cuándo debemos parar porque ya no sea posible encontrar una solución mejor o porque no merezca la pena seguir avanzando, por lo que podemos encontrarnos ante casos en los que no disponemos de un estado final definido. En cierta forma, el proceso que se sigue es **similar al proceso de encontrar óptimos (máximos o mínimos) de funciones**, donde en este caso la función a optimizar es la función de calidad de la solución. Lo normal es que se calculen estos óptimos por medios analíticos aprovechando la expresión de la función y sus propiedades de continuidad y diferenciabilidad, pero en los casos que a menudo nos encontramos en problemas de Inteligencia Artificial las funciones con las que se trabaja no tienen una expresión analítica conocida, o no verifican las condiciones de diferenciabilidad o continuidad necesarias para aplicar los algoritmos de búsqueda de óptimos en funciones. Por ello, tenemos que explorar la función de calidad utilizando únicamente lo que podamos obtener de los vecinos de la solución que hemos encontrado, es decir, haciendo uso únicamente de información local durante el proceso. ## Ascenso de la colina ![](./img/colina.png width=300px align="left")Debido a que en muchos problemas el tamaño del espacio de búsqueda hace que sea inabordable una búsqueda exhaustiva, se deben buscar estrategias diferentes a las utilizadas hasta ahora. En primer lugar, puede haber pocas posibilidades de guardar información para recuperar caminos alternativos dado el gran número de alternativas que se presentan, lo que obliga a imponer restricciones de espacio decidiendo qué nodos deben ser explorados y cuáles deben ser descartados sin volver a ser considerados. Este método general de eliminar ramas de exploración del árbol de búsqueda da lugar a una familia de algoritmos conocida como de **ramificación y poda** (**branch and bound**), en los que olvidamos aquellas opciones que no parecen prometedoras. Estos algoritmos permiten mantener una memoria limitada, ya que desprecian parte del espacio de búsqueda, pero se arriesgan a no hallar la mejor solución, ya que ésta puede estar en la sección del espacio de búsqueda que ha sido eliminada. De los algoritmos de ramificación y poda, unos de los más utilizados son los que se llaman de **ascenso de colinas** (**Hill-climbing**), de los que existen variantes que pueden ser útiles en distintos casos: * **Ascenso de colinas simple**: consiste en elegir siempre el primer operador que suponga una mejora respecto al nodo actual, de manera que no exploramos todas las posibilidades accesibles, ahorrándonos el explorar cierto número de descendientes. Presenta la ventaja de ser más rápido que explorar todas las opciones, pero la desventaja de que hay más probabilidad de no alcanzar las soluciones mejores y quedarse atrapado en lo que se conoce como un **óptimo local**. En cierta forma, sería el equivalente al algoritmo voraz para este tipo de casos pero con información limitada (ya que no explora todos los posibles sucesores).  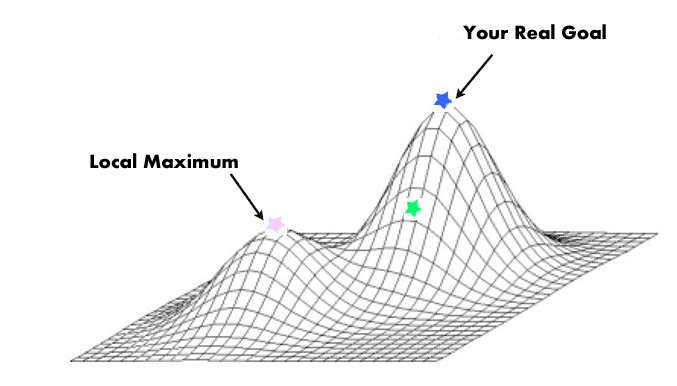* **Ascenso de colinas por máxima pendiente** (**steepest ascent hill climbing**): expande todos los posibles descendientes de un nodo y elige el que suponga la máxima mejora respecto al nodo actual. Este algoritmo supone que la mejor solución la encontraremos a través del sucesor que mayor diferencia tenga respecto a la solución actual, siguiendo una política avariciosa. La utilización de memoria para mantener la búsqueda es nula, ya que solo tenemos en cuenta el nodo mejor. Se pueden hacer versiones que guarden caminos alternativos que permitan una vuelta atrás en el caso de que consideremos que la solución a la que hemos llegado no es suficientemente buena, pero en este caso han de imponerse ciertas restricciones de memoria para no tener un coste en espacio demasiado elevado. ~~~~~~~~ Algoritmo: Ascenso de colinas por máxima pendiente s ← s₀ cont? ← True While cont? do chd ← generar_sucesores(s) chd ← ordenar_y_eliminar_peores(chd, s) if no empty?(chd) then s ← Escoger_mejor(chd) else cont? ← False endif Wend ~~~~~~~~ La estrategia que se usa en este algoritmo hace que sus problemas vengan principalmente derivados por las características de las funciones heurísticas que se utilizan. Por un lado, hemos de considerar que el algoritmo dejará de explorar cuando no encuentra ningún nodo accesible mejor que el actual, pero como no mantiene memoria del camino recorrido, le será imposible reconsiderar su decisión de modo que, si se ha equivocado, puede ocurrir que la solución a la que llegue no sea un óptimo global, sino solo un óptimo local. Esta posibilidad, muy común al atacar problemas reales, se puede presentar cuando la función heurística que se utilice tenga óptimos locales, de forma que, dependiendo de por donde se comience la búsqueda, se acaba encontrando un óptimo distinto.  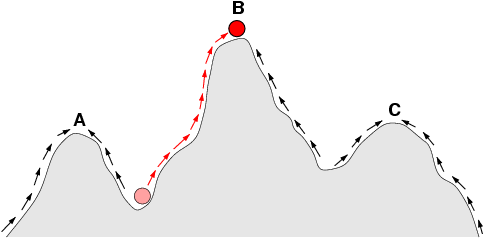* **Búsqueda por ascenso con reinicio aleatorio** (**random restarting hill climbing**): para subsanar este problema se puede intentar la ejecución del algoritmo cierto número de veces desde distintos puntos escogidos aleatoriamente y quedarse solo con la mejor exploración. Por simple que parezca, muchas veces esta estrategia es más efectiva que otros métodos más complejos, y resulta muy barata de implementar. La única dificultad que podemos encontrar radica en la capacidad para poder generar los distintos puntos iniciales de búsqueda, ya que en ocasiones el problema no permite hallar soluciones iniciales con facilidad.  * **Búsqueda en haces** (**beam search**): Un problema con el que se encuentran este tipo de algoritmos son las zonas del espacio de búsqueda en las que la función heurística no es informativa, como por ejemplo las denominadas mesetas y las funciones en escalón, en las que los valores de los nodos vecinos al actual tienen valores iguales, y por lo tanto una elección local no nos permite decidir el camino a seguir. Para evitar estos problemas se debe extender la búsqueda más allá de los vecinos inmediatos para obtener información suficiente para encaminar la búsqueda, pero supone un coste adicional en cada iteración, prohibitivo cuando el factor de ramificación es excesivamente grande. Una alternativa es permitir que el algoritmo guarde parte de los nodos visitados para proseguir la búsqueda por ellos en caso de que el algoritmo se quede atascado en un óptimo local. El algoritmo más utilizado de este tipo es el denominado **búsqueda en haces** (**beam search**). En este algoritmo se va guardando un número $N$ de las mejores soluciones, expandiendo siempre la mejor de ellas. De esta manera no se sigue un solo camino sino $N$ caminos eventualmente distintos. Las variantes que se pueden plantear están en cómo se escogen esas $N$ soluciones que se mantienen. Si siempre se sustituyen las peores soluciones de las $N$ por los mejores sucesores del nodo actual, caemos en el peligro de que todas acaben estando en el mismo camino, reduciendo la capacidad de volver hacia atrás, así que el poder mantener la variedad de las soluciones guardadas es importante. Está claro que cuantas más soluciones se guarden, más posibilidad habrá de encontrar una buena solución, pero se tiene un coste adicional tanto en memoria como en tiempo, ya que habrá que decidir con qué sucesores quedarse y qué soluciones guardadas se sacrifican. ~~~~~~~~ Algoritmo: Búsqueda en Haces s ← s₀ Soluciones_actuales.añadir(s) cont? ← True While cont? do chd ← generar_sucesores(s) soluciones_actuales.actualizar_mejores(chd) if soluciones_actuales.algun_cambio?() then s ← soluciones_actuales.escoger_mejor() else cont? ← False endif wend ~~~~~~~~ El algoritmo acaba cuando ninguno de los sucesores mejora a las soluciones guardadas, lo que quiere decir que todas las soluciones son óptimos locales. # Búsquedas Estocásticas Cuando los espacios de búsqueda son extremadamente grandes o tienen estructuras relativamente complejas, los procedimientos de búsqueda deterministas suelen obtener muy malos resultados. La **Búsqueda Estocástica** introduce factores de aleatoriedad en esos procesos de forma que, bien usada, puede reducir considerablemente la complejidad del problema. Por supuesto, en este proceso se pierde algo, y es que se sustituye la optimalidad por la tratabilidad en tiempo (es decir, el problema se puede resolver en un tiempo razonable, pero ya no podemos estar seguros de que vayamos a encontrar la solución óptima siempre). Hay dos algoritmos de búsqueda estocásticos triviales que podemos identificar claramente: * **Búsqueda Aleatoria**: En cada paso, se selecciona al azar un elemento del espacio de búsqueda y comprobamos si tiene las propiedades deseadas. * **Camino Aleatorio sin información**: En cada paso, se selecciona al azar un vecino del estado actual y nos desplazamos a él. Obviamente, estas dos modificaciones para introducir la aleatoriedad tienen pocas opciones de ser eficientes en espacios relativamente grandes, pero suponen un punto de partida sobre el que construir otros algoritmos estocásticos que arrojan buenos resultados. El más famoso de ellos es el algoritmo del **Templado Simulado** (o **Enfriamiento Simulado**), que veremos a continuación: ## Templado Simulado Hay muchas veces en los que los algoritmos de búsqueda por ascenso se quedan atascados enseguida en óptimos no demasiado buenos. Para estos casos se han diseñado algoritmos que a veces pueden dar soluciones relativamente buenas. El algoritmo del **Templado Simulado** (**Simulated Annealing**) está inspirado en un fenómeno físico que se observa en el templado de metales y en la cristalización de disoluciones: !!!note: Templado Simulado en el Mundo Físico Todo conjunto de átomos o moléculas tiene un estado de energía que depende de cierta función de la temperatura del sistema. A medida que lo vamos enfriando, el sistema va perdiendo energía hasta que se estabiliza. El fenómeno físico que se observa es que, dependiendo de cómo se realiza el enfriamiento, el estado de energía final es muy diferente. Por ejemplo, si una barra de metal se enfría demasiado rápido la estructura cristalina a la que se llega al final está poco cohesionada (un número bajo de enlaces entre átomos) y ésta se rompe con facilidad. Si el enfriamiento se realiza más lentamente, el resultado final es totalmente diferente, el número de enlaces entre los átomos es mayor, y se obtiene una barra mucho más difícil de romper. Durante este enfriamiento controlado se observa que la energía del conjunto de átomos no disminuye de manera constante, sino que a veces la energía total puede ser mayor que en un momento inmediatamente anterior. Esta circunstancia hace que el estado de energía final que se alcanza sea mejor que cuando el enfriamiento se hace rápidamente. A partir de este fenómeno físico se puede obtener un algoritmo que permite, en ciertos problemas, obtener soluciones mejores que las proporcionadas por los algoritmos vistos hasta ahora. En este algoritmo el nodo siguiente a explorar no será siempre el mejor vecino, sino que se elige aleatoriamente (en función de los valores de unos parámetros) de entre todos los vecinos (los buenos y los malos). Una ventaja de este algoritmo es que no hay por qué generar todos los sucesores de un nodo, basta elegir un sucesor al azar y decidir si continuamos por él o no. El algoritmo de templado simulado intenta transportar la analogía física al problema que se quiere solucionar: * En primer lugar, se denomina **función de energía** a la función heurística que mide la calidad de una solución. * Tendremos un parámetro de control que denominaremos **temperatura**, que permitirá controlar el funcionamiento del algoritmo. * También se tendrá una función que dependerá de la temperatura y de la diferencia de calidad entre el nodo actual y un sucesor. Esta función dirigirá la elección de los sucesores de la forma siguiente: * Cuanta mayor sea la temperatura, más probabilidad habrá de que al generar como sucesor un estado peor éste sea elegido. * La elección de un estado peor dependerá de su diferencia de calidad con el estado actual, cuanta más diferencia, menos probabilidad de elegirlo. * El último elemento es la **estrategia de enfriamiento**. Por ejemplo, el algoritmo podría realizar un número total de iteraciones prefijado y cada cierto número de ellas el valor de la temperatura disminuye en cierta cantidad, partiendo desde una temperatura inicial y llegando a cero (o a un valor mínimo) en la última iteración. La elección de estos dos parámetros (**número total de iteraciones** y **número de iteraciones entre cada bajada de temperatura**) determina el comportamiento completo del algoritmo, y puede modificar su eficiencia de forma dramática. Aunque hay algunos resultados teóricos acerca de la influencia de estos parámetros, en general hay que decidir experimentalmente cuál es la temperatura inicial más adecuada y también la forma más adecuada de hacer que vaya disminuyendo. ~~~~~~~~ Algoritmo: Templado Simulado (T₀, s₀, N, γ < 1, ϵ > 0) Temp = T₀ while Temp > ϵ Repeat N: s₁ = Genera_vecino(s₀) ∆E = E(s₀) − E(s₁) if ∆E > 0 s₀ = s₁ else con probabilidad exp(∆E/Temp): s₀ = s₁ Temp = Temp ⋅ γ return s₀ ~~~~~~~~ Como en la analogía física, si el número de pasos es muy pequeño, la temperatura bajará muy rápidamente, y el camino explorado será relativamente aleatorio. Si el número de pasos es más grande, la bajada de temperatura será más suave y la búsqueda será mejor. El algoritmo favorece la disminución de la energía, $E$, ya que $\Delta E>0$ es equivalente a que $E(s_0)>E(s_1)$, y en ese caso $s_1$ se convierte en el estado actual. Cuando $\Delta E < 0$, se tiene que $e^{\Delta E/Temp} < 1$ y, de hecho: $$\displaystyle \lim_{Temp\to 0} e^{\Delta E/Temp}=0$$ por lo que el hecho de admitir nuevos estados que empeoran la búsqueda se hace cada vez más improbable a medida que avanza el algoritmo. Además, los estados que empeoran mucho la energía (es decir, aquellos que hacen que $\Delta E$ sea más negativo) se hacen menos probables que los que la empeoran menos. Es importante observar que la búsqueda se ha transformado en un problema de optimización (en este caso, de minimización), porque realmente pasamos de buscar un estado con ciertas propiedades generales a buscar un estado que tiene valor mínimo respecto a la función de energía considerada. Esta función tiene muchas similitudes con las funciones heurísticas de algoritmos como $A^∗$, ya que de alguna forma mide lo buena, o cerca de la solución ideal, que está el estado actual, pero tiene una ventaja computacional, y es que no imponemos ninguna propiedad adicional (en $A^∗$, la función heurística debía ser admisible para asegurar la convergencia a la solución, por ejemplo). En cualquier caso, a $E$ se le supone un comportamiento bastante básico: 1. $E(s)\geq 0$, para cualquier estado, $s$, de nuestro espacio. 2. $E(s)=0$ solo en el caso en que $s$ sea una solución adecuada del problema. 3. $E(s_1) < E(s_2)$, si $s_1$ es *mejor solución* que $s_2$. 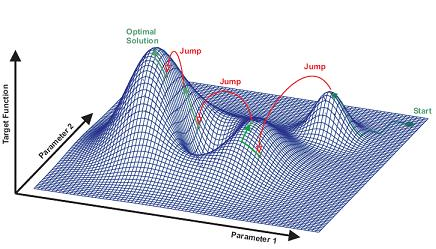Este algoritmo es especialmente bueno para problemas con un espacio de búsqueda grande en los que el óptimo global está rodeado de muchos óptimos locales, ya que le es más fácil escapar de ellos. Se puede utilizar también para problemas en los que encontrar una heurística discriminante es difícil (una elección aleatoria es tan buena como otra cualquiera), ya que en estos casos el algoritmo de ascenso de colinas no tiene mucha información con la que trabajar y se queda atascado enseguida, mientras que el templado simulado puede explorar más espacio de soluciones y tiene mayor probabilidad de encontrar una solución buena. El mayor problema de este algoritmo es determinar los valores de los parámetros, y requiere una importante labor de experimentación que depende de cada problema. Los valores óptimos de estos parámetros varían con el dominio e incluso con el tamaño de la instancia concreta del problema. ## Mejoras al Templado Simulado ### Caso continuo Además de utilizarse en la búsqueda en espacios discretos (a veces también se le llama a este proceso **optimización combinatoria**), el templado simulado puede extenderse a la minimización de funciones continuas, donde si hay mucha variabilidad es muy fácil quedarse atascadas en uno de los muchos mínimos locales. EL problema empeora a medida que la dimensionalidad del problema (el número de variables que intervienen) se vuelve incluso moderadamente grande. El método de templado se ha comparado con otros métodos habituales en búsqueda optimizada continua (como el método simplex de Nelder-Mead, o la búsqueda aleatoria adaptativa) en una serie de funciones de prueba que deben minimizarse (es decir, estamos buscando el mínimo global). En todos los casos, el algoritmo de templado simulado consiguió identificar el mínimo global, cosa que los otros métodos no consiguieron. El templado simulado también fue más eficiente en su búsqueda, en términos de número de evaluaciones de la función (excepto para la función bidimensional de Rosenbrock, utilizada a menudo como función de prueba debido a su multimodalidad, donde el método simplex fue más eficiente), pero sigue siendo un procedimiento costoso desde el punto de vista computacional, ya que el número de evaluaciones crece linealmente con el número de dimensiones. Este coste es menos prohibitivo que el de las otras técnicas, sobre todo porque el coste depende únicamente de la temperatura inicial, lo que significa que el tiempo de cálculo se conoce de antemano, una ventaja del algoritmo. ### Paralelización Uno de los principales problemas del templado simulado, tanto para el caso discreto como continuo, es el elevado tiempo de cálculo para encontrar una solución cercana o exactamente óptima. Este problema surge al proponer y evaluar los valores de las funciones para luego rechazarlos y puede mitigarse en cierta medida paralelizando el proceso. Muchos intentos de paralelización del templado simulado para problemas específicos han tenido éxito, especialmente para problemas bien estudiados como el problema del viajante de negocios. Esta paralelización suele hacerse dividiendo el problema en subproblemas más pequeños, cada uno de los cuales se resuelve mediante templado simulado estándar, como el presentado aquí, y luego recombinando estas soluciones. Dividir el problema de esta manera debe hacerse con mucho cuidado, ya que la alta interdependencia de los subproblemas puede ser problemática. Si los subproblemas interdependientes no se comunican, la recombinación conducirá a una solución que está potencialmente lejos del óptimo global, análoga a las estructuras localmente óptimas del enfriamiento del sistema en su conjunto. Por otra parte, si los subproblemas se comunican, debido a su gran interdependencia, se requiere la comunicación entre los procesadores, lo que sólo supone pequeñas ganancias de eficiencia en comparación con la ejecución de un templado secuencial. Los métodos de paralelización se basan en la identificación de dos clases de problemas: * Los problemas de la clase $K_1$ muestran la característica de que el tiempo que se tarda en generar configuraciones vecinas es aproximadamente igual al tiempo que se tarda en calcular el cambio de coste entre la configuración actual y la propuesta. Un ejemplo de esta clase sería el problema de viajante de negocios. * Los problemas de la clase $K_2$ muestran la característica de que el tiempo para generar una configuración vecina es mucho menor que el tiempo para calcular el cambio en el coste. Un ejemplo de esta clase sería el de asignación de enlaces (la agrupación de una red de componentes de manera que la distancia total entre todos los clusters se minimice).