**Julia Plots: Manual rápido**
Máster Propio en Data Science y Big Data $\mathbf{24/25}$
Dpto. Ciencias de la Computación e Inteligencia Artificial - Universidad de Sevilla
Esta es una guía para ponerte en marcha con `Plots.jl`. Su principal objetivo es presentarte la terminología utilizada en el paquete, cómo utilizar `Plots.jl` en casos de uso común, y ponerte en condiciones de comprender fácilmente el resto del manual. Se recomienda seguir los ejemplos de código dentro del REPL o de un cuaderno interactivo.
## Trazado Básico: Gráficos de líneas
Después de haber instalado `Plots.jl` a través de `Pkg.add(«Plots»)`, el primer paso es inicializar el paquete. Dependiendo de tu ordenador, esto tardará unos segundos:
```julia
using Plots
```
!!!side:1
Para hacer esto en Julia, insertamos un punto justo después de la llamada a la función.
Para empezar, vamos a trazar algunas funciones trigonométricas. Para la coordenada `x`, podemos crear un rango de 0 a 10 de, digamos, 100 elementos. Para la coordenada `y`, podemos crear un vector evaluando `sin(x)` elemento a elemento $^1$. Por último, utilizamos `plot()` para trazar la línea.
```julia
x = range(0, 10, length=100)
y = sin.(x)
plot(x, y)
```

El gráfico se muestra en un panel de gráficos, en una ventana independiente o en el navegador, dependiendo del entorno y del backend (hablaremos de ello más adelante).
Si este es tu primer gráfico de la sesión y tarda un poco en mostrarse, es normal; esta latencia se llama el problema del "tiempo hasta el primer gráfico" (o `TTFP`), y los gráficos posteriores serán rápidos. Debido a la forma en que Julia trabaja bajo el capó, es un problema difícil de resolver, pero se ha avanzado mucho en los últimos años ara reducir este tiempo de compilación inicial.
En `Plots.jl`, cada columna es una **serie**, un conjunto de puntos relacionados que forman líneas, superficies u otras primitivas de trazado. Podemos trazar múltiples líneas trazando una matriz de valores donde cada columna se interpreta como una línea separada. En el siguiente ejemplo, `[y1 y2]` forma una matriz $100\times 2$ ($100$ elementos, $2$ columnas).
```julia
x = range(0, 10, length=100)
y1 = sin.(x)
y2 = cos.(x)
plot(x, [y1 y2])
```

!!!side:2
Notarás que también usamos una macro `@.`. Se trata de una macro de conveniencia que inserta puntos para cada llamada a función a la derecha de la macro, asegurando que toda la expresión será evaluada elemento a elemento. Si introdujéramos los puntos manualmente, necesitaríamos tres de ellos: para el seno, el exponente y la resta, y el código resultante sería menos legible.
Además, podemos añadir más líneas mutando el objeto gráfico. Esto se hace con el comando `plot!`, donde `!` indica que el comando está modificando el trazado actual $^2$.
```julia
y3 = @. sin(x)^2 - 1/2 # equivalent to y3 = sin.(x).^2 .- 1/2
plot!(x, y3)
```

Ten en cuenta que podríamos haber hecho lo mismo que arriba utilizando una variable gráfica explícita, a la que llamamos `p`:
```julia
x = range(0, 10, length=100)
y1 = sin.(x)
y2 = cos.(x)
p = plot(x, [y1 y2])
y3 = @. sin(x)^2 - 1/2
plot!(p, x, y3)
```
En los casos en que se omite la variable de trazado, `Plots.jl` utiliza la variable global `Plots.CURRENT_PLOT` automáticamente.
### Guardar Figuras
El guardado de gráficos se realiza mediante el comando `savefig`. Por ejemplo:
```julia
savefig("myplot.png") # guarda el CURRENT_PLOT como un .png
savefig(p, "myplot.pdf") # guarda el gráfico de p como un gráfico vectorial .pdf
```
!!!side:3
Y otras que pueden ayudar y que no se exportan por defecto.
También existen funciones adecuadas `png`, `Plots.pdf` $^3$. Con ellas, la extensión se omite en el nombre del archivo. Por ejemplo:
```julia
png("myplot")
Plots.pdf(p, "myplot")
```
## Atributos de la gráfica
Necesitamos ahora dar estilo a nuestras gráficas. En `Plots.jl`, los modificadores de los gráficos se llaman **atributos**, y sigue dos reglas simples con los datos y los atributos:
* Los argumentos posicionales corresponden a los datos de entrada
* Los argumentos de palabra clave corresponden a los atributos
Así que algo como `plot(x, y, z)` son datos tridimensionales para gráficos 3D sin atributos, mientras que `plot(x, y, attribute=value)` son datos bidimensionales con un atributo asignado a algún valor.
Por ejemplo, podemos cambiar el ancho de línea con `linewidth` (o su alias `lw`), cambiar las etiquetas de la leyenda con `label` y añadir un título con `title`. Observa que `["sin(x)" "cos(x)"]` tiene el mismo número de columnas que los datos. Además, como el ancho de línea se atribuye a `[y1 y2]`, ambas líneas se verán afectadas por el valor asignado. Apliquemos todo esto a nuestro gráfico anterior:
```julia
x = range(0, 10, length=100)
y1 = sin.(x)
y2 = cos.(x)
plot(x, [y1 y2], title="Trigonometric functions", label=["sin(x)" "cos(x)"], linewidth=3)
```

Cada atributo puede aplicarse también mutando el gráfico con una función modificadora. Algunos atributos tienen sus propias funciones modificadoras, mientras que a otros se puede acceder a través de `plot!(atributo=valor)`. Por ejemplo, el atributo `xlabel` añade una etiqueta para el eje `x`. Podemos especificarla en el comando `plot`. Podemos especificarlo en el comando de trazado con `xlabel=...`, o podemos utilizar la función modificadora de abajo para añadirlo después de que el trazado ya haya sido generado:
```julia
xlabel!("x")
```
Cada función modificadora es el nombre del atributo seguido de `!`. Esto utilizará implícitamente el atributo global `Plots.CURRENT_PLOT`. Podemos aplicarlo a otros objetos gráficos mediante `attribute!(p, value)`, donde `p` es el nombre del objeto gráfico que queremos modificar.
Vamos a utilizar las palabras clave y las funciones modificadoras indistintamente para realizar algunas modificaciones comunes a nuestro ejemplo, que se enumeran a continuación. Observará que para los atributos `ls` y `legend`, los valores incluyen dos puntos `:`. Los dos puntos denotan un símbolo en Julia. Se utilizan comúnmente para los valores de los atributos en `Plots.jl`, junto con cadenas y números.
* Etiquetas para las líneas individuales, que se ven en la leyenda
* Anchos de línea (usaremos el alias `lw` en lugar de `linewidth`)
* Estilos de línea (usaremos el alias `ls` en lugar de `linestyle`)
* Posición de la leyenda (fuera del gráfico, ya que por defecto saturaría el gráfico)
* Columnas de la leyenda (3, para usar mejor el espacio horizontal)
* Límites X para ir de `0` a `2pi`
* Título del gráfico y etiquetas de los ejes.
```julia
x = range(0, 10, length=100)
y1 = sin.(x)
y2 = cos.(x)
y3 = @. sin(x)^2 - 1/2
plot(x, [y1 y2], label=["sin(x)" "cos(x)"], lw=[2 1])
plot!(x, y3, label="sin(x)^2 - 1/2", lw=3, ls=:dot)
plot!(legend=:outerbottom, legendcolumns=3)
xlims!(0, 2pi)
title!("Trigonometric functions")
xlabel!("x")
ylabel!("y")
```

Observa que `y3` se representa como una línea de puntos. Esto es distinto de un gráfico de dispersión de los datos.
### Gráficos a escala logarítmica
A veces es necesario representar los datos a través de órdenes de magnitud. En este caso, los atributos `xscale` e `yscale` pueden establecerse a `:log10`. También pueden ajustarse a `:identity` para mantener la escala lineal. Hay que tener cuidado de que los datos y los límites sean positivos.
```julia
x = 10 .^ range(0, 4, length=100)
y = @. 1/(1+x)
plot(x, y, label="1/(1+x)")
plot!(xscale=:log10, yscale=:log10, minorgrid=true)
xlims!(1e+0, 1e+4)
ylims!(1e-5, 1e+0)
title!("Log-log plot")
xlabel!("x")
ylabel!("y")
```

### Cadenas de ecuaciones LaTeX
`Plots.jl` funciona con `LaTeXStrings.jl`, un paquete que permite al usuario escribir ecuaciones LaTeX en literales de cadena. Para instalarlo, escribe `Pkg.add("LaTeXStrings")`. La forma más sencilla de utilizarlo es anteponer `L` a una cadena con formato LaTeX. Si la cadena es una mezcla entre texto normal y ecuaciones LaTeX, inserta signos de dólar `$` según sea necesario.
```julia
using LaTeXStrings
x = 10 .^ range(0, 4, length=100)
y = @. 1/(1+x)
plot(x, y, label=L"\frac{1}{1+x}")
plot!(xscale=:log10, yscale=:log10, minorgrid=true)
xlims!(1e+0, 1e+4)
ylims!(1e-5, 1e+0)
title!(L"Log-log plot of $\frac{1}{1+x}$")
xlabel!(L"x")
ylabel!(L"y")
```

## Cambiando el Tipo de Serie: Gráficos de dispersión
!!!side:4
Los tipos de series disponibles dependen del backend. Como describiremos más adelante, otras bibliotecas pueden añadir nuevos tipos de series utilizando **recetas**.
En `Plots.jl`, las formas de graficar una serie se llama **tipo de serie** $^4$. Una línea es un tipo de serie. Sin embargo, un gráfico de dispersión es otro tipo de serie que se utiliza habitualmente.
Empecemos de nuevo con la función seno, pero esta vez definiremos un vector llamado `y_noisy` que añade algo de aleatoriedad. Podemos cambiar el tipo de serie utilizando el atributo `seriestype`.
```julia
x = range(0, 10, length=100)
y = sin.(x)
y_noisy = @. sin(x) + 0.1*randn()
plot(x, y, label="sin(x)")
plot!(x, y_noisy, seriestype=:scatter, label="data")
```

Para cada tipo de serie incorporada, existe una función abreviada para llamar directamente a ese tipo de serie que coincide con su nombre. Maneja los atributos igual que el comando `plot`, y tiene una forma mutante que termina en `!`. Por ejemplo, podemos escribir la última línea como:
```julia
scatter!(x, y_noisy, label="data")
```
Los gráficos de dispersión tendrán algunos atributos comunes relacionados con los marcadores. Aquí hay un ejemplo del mismo gráfico, pero con algunos atributos para hacer el gráfico más presentable. Se utilizan muchos alias para abreviar, y la lista siguiente no es en absoluto exhaustiva.
* `lc` para `linecolor`
* `lw` para `linewidth`
* `mc` para `markercolor`
* `ms` para `markersize`
* `ma` para `markeralpha`
```julia
x = range(0, 10, length=100)
y = sin.(x)
y_noisy = @. sin(x) + 0.1*randn()
plot(x, y, label="sin(x)", lc=:black, lw=2)
scatter!(x, y_noisy, label="data", mc=:red, ms=2, ma=0.5)
plot!(legend=:bottomleft)
title!("Sine with noise")
xlabel!("x")
ylabel!("y")
```

## Backends para Graficar
Plots.jl` es un metapaquete para graficar, es decir: es una interfaz sobre diferentes librerías de graficación. Lo que `Plots.jl` hace en realidad es interpretar tus comandos y luego generar los gráficos usando otra librería de gráficos, llamada **backend**. Lo bueno de esto es que puedes usar muchas librerías de ploteo diferentes con la sintaxis de `Plots.jl`, y veremos en un momento que `Plots.jl` añade nuevas características a cada una de estas librerías.
Cuando empezamos a graficar arriba, nuestras gráficas utilizaron el backend `GR` por defecto. Sin embargo, si queremos un backend de graficación diferente que plotee en una bonita GUI o en el panel de gráficos de VS Code, necesitaremos un backend que sea compatible con estas características. Algunos backends comunes para esto son `PythonPlot` y `Plotly`. Por ejemplo, para instalar `PythonPlot`, simplemente escribe el comando `Pkg.add("PythonPlot")` en la REPL; para instalar `Plotly`, escribe `Pkg.add("PlotlyJS")`.
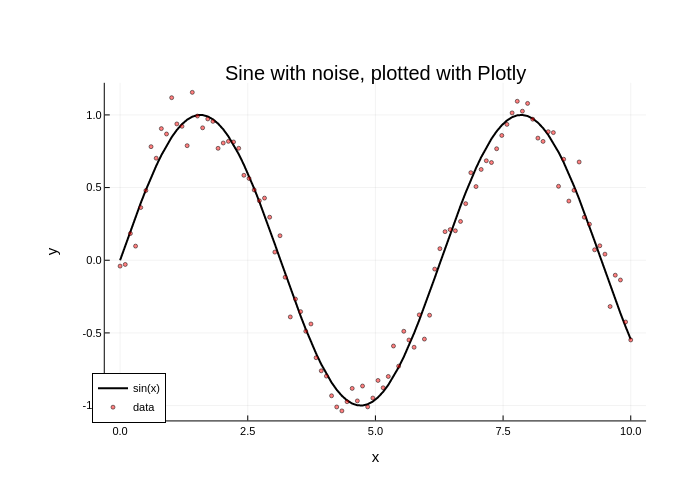
Podemos elegir específicamente el backend utilizando el nombre del backend en minúsculas como una función. Vamos a trazar el ejemplo de arriba usando `Plotly` y luego `GR`:
```julia
plotlyjs() # set the backend to Plotly
x = range(0, 10, length=100)
y = sin.(x)
y_noisy = @. sin(x) + 0.1*randn()
# this plots into a standalone window via Plotly
plot(x, y, label="sin(x)", lc=:black, lw=2)
scatter!(x, y_noisy, label="data", mc=:red, ms=2, ma=0.5)
plot!(legend=:bottomleft)
title!("Sine with noise, plotted with Plotly")
xlabel!("x")
ylabel!("y")
png("plotlyjs_tutorial") #hide
```
```julia
gr() # set the backend to GR
# this plots using GR
plot(x, y, label="sin(x)", lc=:black, lw=2)
scatter!(x, y_noisy, label="data", mc=:red, ms=2, ma=0.5)
plot!(legend=:bottomleft)
title!("Sine with noise, plotted with GR")
xlabel!("x")
ylabel!("y")
```
Cada backend aporta una sensación muy diferente. Algunos tienen interactividad, otros son más rápidos y pueden manejar un gran número de puntos de datos, y algunos pueden hacer gráficos en 3D. Algunos backends como `GR` pueden guardar gráficos vectoriales y PDFs, mientras que otros como Plotly sólo pueden guardar PNGs.
## Graficar en scripts
Al principio del tutorial, recomendamos seguir los ejemplos de código en una sesión interactiva por la siguiente razón: intenta añadir esos mismos comandos de graficos a un script. Ahora llama al script... ¿y el gráfico no aparece? Esto se debe a que Julia en uso interactivo a través del REPL llama a `display` en cada variable que es devuelta por un comando sin punto y coma `;`. En cada caso anterior, el uso interactivo estaba llamando automáticamente a `display` en los objetos de trazado devueltos.
En un script, Julia no hace despliegues automáticos, razón por la cual `;` no es necesario. Sin embargo, si queremos mostrar nuestros gráficos en un script, sólo tenemos que añadir la llamada a `display`. Por ejemplo:
```julia
display(plot(x, y))
```
Alternativamente, podríamos llamar a `gui()` al final para hacer lo mismo. Por último, si tenemos un objeto gráfico `p`, podemos escribir `display(p)` para mostrar el gráfico.
## Combinar varias gráficas como subgráficas
Podemos combinar múltiples gráficos juntos como subgráficos utilizando **layouts** (diseños). Hay muchos métodos para hacer esto, y mostraremos dos métodos simples para generar diseños simples.
El primer método consiste en definir un diseño que dividirá una serie. El comando `layout` toma una 2-tupla `layout=(N, M)` que construye una rejilla $N\times M$ de gráficos, y automáticamente dividirá una serie para estar en cada gráfico. Por ejemplo, si escribimos `layout=(3, 1)` en un gráfico con tres series, obtendremos tres filas de gráficos, cada una con una serie.
Definamos algunas funciones y representémoslas en gráficos separados. Puesto que sólo hay una serie en cada gráfico, también eliminaremos la leyenda en cada uno de los gráficos utilizando `legend=false`.
```julia
x = range(0, 10, length=100)
y1 = @. exp(-0.1x) * cos(4x)
y2 = @. exp(-0.3x) * cos(4x)
y3 = @. exp(-0.5x) * cos(4x)
plot(x, [y1 y2 y3], layout=(3, 1), legend=false)
```

También podemos utilizar diseños en gráficas de objetos de gráficas. Por ejemplo, podemos generar cuatro gráficas separadas y hacer una única que las combine en una cuadrícula de $2\times 2$.
```julia
x = range(0, 10, length=100)
y1 = @. exp(-0.1x) * cos(4x)
y2 = @. exp(-0.3x) * cos(4x)
y3 = @. exp(-0.1x)
y4 = @. exp(-0.3x)
y = [y1 y2 y3 y4]
p1 = plot(x, y)
p2 = plot(x, y, title="Title 2", lw=3)
p3 = scatter(x, y, ms=2, ma=0.5, xlabel="xlabel 3")
p4 = scatter(x, y, title="Title 4", ms=2, ma=0.2)
plot(p1, p2, p3, p4, layout=(2,2), legend=false)
```

Ten en cuenta que los atributos en las gráficas individuales se aplican a esas gráficas individuales, mientras que el atributo `legend=false` en la llamada final `plot` se aplica a todas las subgráficas.
## Recetas de Gráficas y bibliotecas de recetas
Las recetas de gráficos son extensiones del framework `Plots.jl`. Añaden:
1. Nuevos comandos `plot` a través de **recetas de usuario**.
2. Interpretaciones por defecto de los tipos de Julia como datos de gráficos a través de **recetas de tipo**.
3. Nuevas funciones para generar gráficos mediante **recetas de gráficos**.
4. Nuevos tipos de series mediante **recetas de series**.
Escribir tus propias recetas es un tema avanzado que no nos interesa ahora mismo, pero presentaremos las formas en que se utiliza una receta.
Las recetas están incluidas en muchas bibliotecas de recetas. Dos bibliotecas de recetas fundamentales son [PlotRecipes.jl](https://github.com/JuliaPlots/PlotRecipes.jl) y [Stats`Plots.jl`](https://github.com/JuliaPlots/Stats`Plots.jl`). Echemos un vistazo a Stats`Plots.jl`, que añade un montón de recetas, pero en las que nos centraremos son:
1. Añade una receta de tipo para `Distribution`s.
2. Añade una receta de gráfica para histogramas marginales.
3. Añade un montón de nuevas series de gráficos estadísticos.
Además de las recetas, Stats`Plots.jl` también proporciona una macro especializada `@df` para trazar directamente desde tablas de datos.
### Uso de recetas de usuario
Una receta de usuario dice cómo interpretar los comandos de graficación en un nuevo tipo de datos. En este caso, `StatsPlots.jl` tiene una macro `@df` que permite trazar un `DataFrame` directamente utilizando los nombres de las columnas. Construyamos un `DataFrame` con las columnas `a`, `b`, y `c`, y digamos a `Plots.jl` que use `a` como eje `x` y trace las series definidas por las columnas `b` y `c`:
```julia
# Pkg.add("StatsPlots")
# required for the dataframe user recipe
using StatsPlots
# now let's create the dataframe
using DataFrames
df = DataFrame(a=1:10, b=10*rand(10), c=10*rand(10))
# plot the dataframe by declaring the points by the column names
# x = :a, y = [:b :c] (notice that y has two columns!)
@df df plot(:a, [:b :c])
```

No hay mucho más que hacer, todos los comandos de antes (atributos, tipos de series, etc.) seguirán funcionando con estos datos:
```julia
# x = :a, y = :b
@df df scatter(:a, :b, title="My DataFrame Scatter Plot!")
```

### Uso de una receta tipo
Además, `StatsPlots.jl` amplía `Distributions.jl` añadiendo una receta de tipo para sus tipos de distribución, de modo que puedan interpretarse directamente como datos de graficación:
```julia
using Distributions
plot(Normal(3, 5), lw=3)
```

Las recetas de tipos son una forma muy cómoda de graficar un tipo especializado que no requiere más intervención.
### Uso de recetas de gráficos
`StatsPlots.jl` añade el gráfico múltiple `marginhist` a través de una receta de gráficos. Para nuestros datos, utilizaremos el famoso conjunto de datos `iris` de RDatasets:
```julia
# Pkg.add("RDatasets")
using RDatasets, StatsPlots
iris = dataset("datasets", "iris")
@df iris marginalhist(:PetalLength, :PetalWidth)
```
Aquí, `iris` es un DataFrame; utilizando la macro `@df` descrita anteriormente, damos a `marginalhist(x, y)` los datos de las columnas `PetalLength` y `PetalWidth`.
Observa que esto es más que una serie, ya que genera múltiples series (es decir, hay múltiples gráficos debido a los hists de la parte superior y derecha). Por lo tanto, una receta de gráficos no es sólo una serie, sino también algo así como un nuevo comando `plot`.
### Uso de recetas de series
`StatsPlots.jl` también introduce nuevas recetas de series. La clave es que no tienes que hacer nada diferente, tras `using StatsPlots`, puedes simplemente usar esas nuevas recetas de series como si estuvieran incorporadas en las librerías de ploteo. Usemos el gráfico de tipo violin con algunos datos aleatorios:
```julia
y = rand(100, 4)
violin(["Series 1" "Series 2" "Series 3" "Series 4"], y, legend=false)
```

Podemos añadir un `boxplot` encima utilizando los mismos comandos de mutación que antes:
```julia
boxplot!(["Series 1" "Series 2" "Series 3" "Series 4"], y, legend=false)
```

## Cosas adicionales
Dada la fácil extensibilidad de `Plots.jl`, hay muchas otras cosas que puedes probar. Aquí tienes una pequeña lista de complementos muy útiles:
- [PlotThemes.jl](https://github.com/JuliaPlots/PlotThemes.jl) te permite cambiar el esquema de color de tus gráficos. Por ejemplo, `theme(:dark)` añade un tema oscuro.
- [StatsPlots.jl](https://github.com/JuliaPlots/StatsPlots.jl) añade funciones para la visualización de análisis estadísticos.
- La [página de ecosistema](https://docs.juliaplots.org/latest/ecosystem/) muestra muchos otros paquetes que tienen recetas y extienden la funcionalidad de `Plots.jl`.