**MDSBD**
Toma de Decisiones bajo Incertidumbre ... con Julia
!!!Warning: Contenido
1. [Teoría](RLJulia.md.html) (este documento).
2. [Transparencias usadas en clase](RLJuliaSlides.md.html).
3. [Documento de instalación de Julia](installJulia.md.html).
3. Ejemplos en Julia: [](rl_mdp.jl), [](rl_tdlearn.jl).
4. Problema a resolver:
* *Da un MDP que permita modelar un laberinto (como una malla rectangular) con el fin de encontrar una solución desde una casilla de salida a una de llegada.*
* Se tendrá en cuenta si solo se da una solución formal o se añade una implementación en Julia (que no es obligatoria, pero sí favorable).
* Las condiciones del problema son completamente abiertas, por lo que permite más de una aproximación como solución.
# Introducción
Este módulo tiene un doble objetivo:
1. Presentar los fundamentos de la Toma de Decisiones bajo Incertidumbre (en particular, lo que se conoce como Aprendizaje por Refuerzo, RL) de una forma liviana (y, por supuesto, no completa).
1. Presentar el lenguaje de programación Julia desde un punto de vista operativo como representante de lo que se llama Computación Científica.
Aunque presentaremos algunos conceptos definiendo las estructuras y algoritmos básicos de forma directa en Julia (sin ayuda de librerías especializadas), los ejemplos más depurados harán uso de paquetes específicamente desarrollados para ello (como `POMDPs.jl`, una colección de herramientas en Julia que tienen como objetivo facilitar el uso de estructuras y algoritmos propios del modelado de MDPs, POMDPs, y RL).
Así pues, vamos a intentar cubrir algunas tareas adicionales en este mini-módulo:
1. Por qué Julia es un lenguaje que merece la pena conocer (y especialmente interesante si se quiere hacer Computación Científica).
1. Fundamentos de la Toma de Decisiones y sus aplicaciones.
1. Primer contacto con la librería `POMDPs.jl`.
1. Ver algunos de los casos de éxito más característicos que hacen uso (de una forma u otra) del RL.
Debido a que se pretende proporcionar una visión rápida, no seremos muy cautos a la hora de presentar los fundamentos teóricos y, además, habrá características de la librería que los veremos muy superficialmente (y quizás queden sin aclaración).
# ¿Por qué Julia?
## ¿Por qué se creó Julia?
El lenguaje Julia ha sido diseñado para ser rápido y dinámico. En palabras de sus desarrolladores:
!!!
*Queríamos un lenguaje que fuera de código abierto, con una licencia liberal. Queremos la velocidad de C con el dinamismo de Ruby. Queremos un lenguaje que sea homoicónico, con verdaderas macros como Lisp, pero con una notación matemática obvia y familiar como Matlab. Queremos algo tan útil para la programación general como Python, tan fácil para la estadística como R, tan natural para el procesamiento de cadenas como Perl, tan potente para el álgebra lineal como Matlab, tan bueno para unir programas como el shell de Linux. Algo que sea sencillísimo de aprender, pero que mantenga contentos a los hackers más serios. Lo queremos interactivo y compilado. (¿Mencionamos que debería ser tan rápido como C?).*
([Why We Created Julia](https://julialang.org/blog/2012/02/why-we-created-julia/), por Jeff Bezanson, Stefan Karpinski, Viral B. Shah, Alan Edelman)
Pero más famoso que este texto de motivación, un famoso lema que quedó en las primeras versiones de Julia (allá por 2012) dice:
!!!
*Camina como Python, corre como C.*
(De hecho, hay una comparación más que se perdió con el tiempo, quizás por lejanía con el programador más actual: *se siente como Lisp*.)
## Velocidad
Muchos investigadores y programadores se sienten atraídos por Julia debido a su velocidad. De hecho, Julia es uno de los pocos lenguajes que forman parte del exclusivo club de los [`petaflops`](https://www.hpcwire.com/off-the-wire/julia-joins-petaflop-club/) (junto con C, C++ y Fortran).

## El problema de los dos lenguajes
!!!
¿Alguna vez has escrito y creado prototipos de código en un lenguaje de alto nivel y luego has tenido que reescribirlo o portarlo a otro lenguaje para que funcionara mejor?
Para ejecutar código en cualquier lenguaje de programación es necesario realizar algún tipo de traducción a código máquina (ensamblador), pero la forma en que se realiza esta traducción difiere entre lenguajes de programación:
* Los lenguajes *interpretados*, como Python y R, traducen las instrucciones línea a línea.
* Los lenguajes compilados, como C/C++ y Fortran, son traducidos por un compilador antes de ejecutar el programa.
La ventaja de los lenguajes interpretados es que son más fáciles de leer y escribir porque hay que proporcionar menos información sobre aspectos como tipos y tamaños de matrices. **Por tanto, la productividad del programador** es mayor en los lenguajes interpretados, pero los lenguajes compilados suelen ser **más rápidos en órdenes de magnitud** porque el compilador puede realizar optimizaciones durante la traducción a ensamblador.
En muchos aspectos **Julia parece un lenguaje interpretado**, y en su mayor parte se comporta como tal. Pero, antes de que cada función sea ejecutada, la Máquina Virtual de Bajo Nivel (LLVM) del motor de Julia la compilará *justo a tiempo* (**JIT**). De esta forma, se obtiene la flexibilidad de un lenguaje interpretado y la velocidad de ejecución del lenguaje compilado a costa de esperar un poco más para la primera ejecución de cualquier función (las versiones compiladas se mantienen para su reutilización mientras no se realicen cambios en su contenido, de manera que no es necesario compilar de nuevo las funciones si simplemente se van a reutilizar con otros datos de entrada, que suele ser lo más común).
## Componibilidad
Julia es altamente [`componible`](https://en.wikipedia.org/wiki/Composability), lo que significa que facilita enormemente la reutilización de componentes/paquetes que han sido desarrollados independientemente sin necesidad de estar adaptándolo continuamente ni creando interfaces/APIs para ser usados juntos, y el resultado es exactamente el que se había esperado.
Podemos mostrar un ejemplo de esta capacidad por la interacción entre [`DifferentialEquations.jl`](https://diffeq.sciml.ai/stable/) (un paquete para resolver ecuaciones diferenciales) y [`Measurements.jl`](https://github.com/JuliaPhysics/Measurements.jl) (un paquete para trabajar con magnitudes donde las incertidumbres se cuentan explícitamente).
Normalmente, la ecuación del péndulo simple se resuelve por medio de la ecuación diferencial asociada trabajando con valores reales sin considerar los posibles errores de medición (inseparables de una medición real). Se esperaría que, a pesar de tener un paquete que permite trabajar con esta incertidumbre en la medición de una manera directa, tuviéramos que elegir entre adaptar el paquete de ecuaciones diferenciales para tratar con datos imprecisos, o convertir los datos imprecisos en representantes numéricos precisos (sabiendo que ignoramos el error de medición y considerando una especie de caso medio).
Sin embargo, Julia permite mezclar simultáneamente ambos paquetes de forma que el usuario no tiene que preocuparse por transformaciones intermedias ni adaptaciones adicionales de código.
La ecuación diferencial (de segundo orden) que rige el movimiento del péndulo es:
$$\ddot{\theta} + \frac{g}{L}\theta = 0$$
Podemos resolver esta ecuación para un caso real considerando mediciones de incertidumbre de forma tan sencilla como muestra el siguiente código (adaptado de https://tutorials.sciml.ai/ ):
```julia
using DifferentialEquations, Measurements, Plots
g = 9.79 ± 0.02; # Constante Gravitacional
L = 1.00 ± 0.01; # Longitud del Péndulo
# Condiciones Iniciales
u₀ = [0 ± 0, π / 3 ± 0.02] # Velocidad y Ángulos iniciales
tspan = (0.0, 6.3)
# Definición del problema
function simplependulum(du,u,p,t)
θ = u[1]
dθ = u[2]
du[1] = dθ
du[2] = -(g/L) * sin(θ)
end
# Llamada al solver
prob = ODEProblem(simplependulum, u₀, tspan)
sol = solve(prob, Tsit5(), reltol = 1e-6)
plot(sol.t, getindex.(sol.u, 2), label = "Péndulo")
```
El resultado es una aproximación numérica que ofrece, además, el error esperado en cada evaluación, y que se debe a la imprecisión de los datos de entrada que se dieron al solver diferencial:
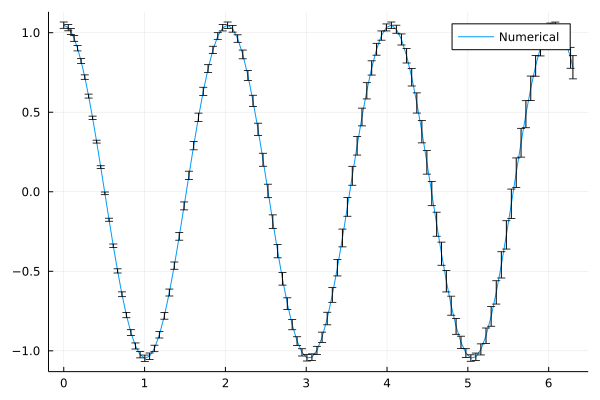
## Inconvenientes y soluciones
Puede ser interesante destacar algunas de las características que más llaman la atención del programador recién llegado a Julia (tanto las positivas como las negativas):
**Tiempo empleado para el primer gráfico**: Si abres el REPL de Julia y escribes un comando de trazado (como `plot`), tardará unos segundos en aparecer porque Julia necesita *precompilar* el paquete `Plots.jl` en tu máquina (por defecto, solo se baja los fuentes y se compilarán por completo en local la primera vez que se usan, o cuando son actualizados), que es bastante grande. Esto hace que Julia no sea adecuado para pequeños scripts que se deben llamar con frecuencia para realizar un trabajo ligero.
- Solución 1: Utiliza sesiones REPL de larga duración para reducir el efecto de las primeras compilaciones.
- Solución 2: Se puede usar [`PackageCompiler.jl`](https://github.com/JuliaLang/PackageCompiler.jl) para crear un paquete precompilado que incluya las librerías base de Julia y que se pueda ejecutar en un ordenador diferente.
**Ecosistema**: El ecosistema de paquetes es menos maduro que, por ejemplo, los de Python y R, por lo que es posible que no encuentres un paquete que se corresponda exactamente con tu paquete favorito en otro lenguaje.
- Solución 1: Es sencillo usar librerías externas de Python o R desde Julia.
- Solución 2: Escribir código rápido en Julia es más fácil que en la mayoría de los otros lenguajes, así que si te gusta o necesitas tener más control sobre las librerías que usas, puedes considerar escribir tu propia versión.
**Rápida evolución de los paquetes**: Aunque la mayoría de los paquetes principales se han estabilizado, todavía hay muchos paquetes que sufren grandes y frecuentes cambios que pueden *romper* el código.
- Solución: Julia viene con un potente gestor de paquetes y soporte incorporado para entornos de software aislados donde las dependencias se pueden registrar con exactitud y donde es fácil crear entornos personalizados de desarrollo (que usan, por ejemplo, versiones anteriores de cada paquete).
**Gran huella de memoria**: Debido a la precompilación de las librerías Base de Julia, el tiempo de ejecución de un proceso en marcha puede ser muy grande. Esto puede restar memoria valiosa para el cálculo real.
- Solución: Los tiempos de ejecución se van aligerando en cada nueva versión de Julia (en el momento de escribir este módulo, acaba de aparecer la versión 1.9, que muestra unas mejoras en tiempo y memoria francamente llamativas), de forma que el usuario no tiene que preocuparse por optimizar su código, y es el compilador el que se encarga de las optimizaciones que van apareciendo.
# Toma de Decisiones bajo Incertidumbre
Muchos problemas importantes implican la toma de decisiones en condiciones de incertidumbre. A la hora de diseñar sistemas automatizados de toma de decisiones (o sistemas de apoyo a la toma de decisiones) es importante tener en cuenta diversas fuentes de incertidumbre y equilibrar cuidadosamente los múltiples objetivos.
En este módulo queremos analizar estos retos desde una perspectiva computacional, con el fin de proporcionar una teoría que sustenta los modelos de toma de decisiones bajo incertidumbre y presentar algunos de los enfoques computacionales más comunes que se han desarrollado.
## Toma de decisiones
La **toma de decisiones** en agentes se refiere al proceso dinámico mediante el cual un **agente inteligente** selecciona una acción entre varias opciones posibles para lograr un objetivo o resolver un problema. En este sentido, muchas veces se distingue entre objetivos de **un paso** (si toda nuestra meta se obtiene en una sola acción del agente), de **horizonte finito** (cuando el número de acciones del agente está acotado por una longitud conocida a priori), o de **horizonte infinito** (cuando no estamos en las condiciones anteriores).
!!!
Un agente es un programa o entidad autónoma que puede percibir su entorno y actuar en, y sobre, él para alcanzar sus objetivos.
La toma de decisiones en agentes se basa en la utilización de algoritmos y técnicas de inteligencia artificial que permiten al agente evaluar las opciones disponibles y seleccionar la acción más adecuada. Para ello, el agente debe contar con información sobre su entorno, los objetivos que se pretenden alcanzar y las posibles acciones que puede tomar.
La toma de decisiones en agentes se utiliza en una amplia variedad de aplicaciones de inteligencia artificial, desde la robótica, hasta la automatización de procesos, pasando por todo tipo de asistentes virtuales.
Además, tanto el planteamiento del problema como sus posibles aproximaciones pueden cambiar radicalmente si pasamos de un entorno en el que consideramos un solo agente a uno en el que hay diversos agentes, trabajando de forma colaborativa o competitiva. En el caso de un conjunto de agentes entraríamos en el terreno de los **Sistemas Multiagente** (MAS), que no abordaremos en esta sesión.
En general, la toma de decisiones por parte de agentes se divide en dos fases: la fase de **observación** y la fase de **acción**.
* En la fase de observación, el agente recopila información sobre su entorno mediante *sensores* y procesa la información para obtener una representación adecuada del estado actual del entorno.
* En la fase de acción, el agente selecciona la acción más adecuada para lograr sus objetivos y la ejecuta mediante *actuadores*.
!!!
Más detalladamente, el **ciclo de observación-acción** que se genera por la interacción entre el agente y el entorno puede modelarse como:
1. El agente, en el momento $t$, recibe una **observación** del entorno, $o_t$. Las observaciones pueden realizarse, por ejemplo, a través de sensores biológicos, como en el caso de los seres vivos, o mediante la transmisión de información por canales artificiales diseñados para ese fin. Debe destacarse que, en cualquier caso, las observaciones son a menudo incompletas o ruidosas: los humanos pueden no ver un objeto que se aproxima o un sistema de detección electromagnético puede pasar por alto un evento debido a una interferencia electromagnética o a una falta de precisión en su diseño.
2. Con el fin de alcanzar un **objetivo predefinido**, el agente elige entonces una **acción**, $a_t$, a través de un proceso de **toma de decisiones**, que puede tener un efecto (a veces, no determinista, debido a múltiples fuentes de incertidumbre) en el entorno.
Aunque agentes hay de muchos tipos, nosotros nos centraremos en los agentes que interactúan de **forma inteligente** para alcanzar sus objetivos a lo largo del tiempo, y con preferencia modelaremos problemas con tiempo discreto, no continuo (el caso continuo se estudia en profundidad en el área de la *Teoría de Control*):
!!!
Entre las diversas fuentes de incertidumbre que pueden intervenir en la capacidad del agente para **elegir la acción** que le acerque a sus objetivos de **la mejor manera posible** podemos destacar, fundamentalmente, las cuatro siguientes (no excluyentes entre sí):
- **Incertidumbre en los resultados**, donde los efectos de las acciones realizadas por el agente son inciertos.
Por ejemplo, un agente puede intentar atacar a un enemigo, pero no está seguro del resultado que tendrá el ataque, pudiendo salir herido él mismo, vencer al enemigo, o seguir bajo el estado de confrontación (aunque, posiblemente, con características distintas).
- **Incertidumbre del modelo**, donde nuestro modelo del problema es incierto.
Por ejemplo, podemos suponer que el modelo que rige la meteorología es uno en particular, pero no coincide con la evolución y cambios que se producen en el mundo real (a veces puede ser una aproximación, y otras ofrecer un resultado completamente distinto e inesperado).
- **Incertidumbre de estado**, cuando el estado real del entorno es incierto.
Por ejemplo, podemos suponer que la salida de un edificio está en un lugar determinado, pero no estamos seguros de que sea así, por lo que planificar la evacuación del mismo podría tener en consideración la validez o no de esa suposición.
- **Incertidumbre de interacción**, cuando el comportamiento de los demás agentes que interactúan en el entorno es incierto.
Por ejemplo, en un entorno multiagente, uno de ellos puede no tener seguridad acerca de las acciones que realizarán el resto de agentes cuando intente realizar algún tipo de acción conjunta (sea colaborativa o no).
La toma de decisiones en presencia de incertidumbre se convierte en una pieza fundamental en el campo de la Inteligencia Artificial, así como en muchos otros campos que precisan de un modelado eficiente del problema a tratar, y el comportamiento esperado debería ser óptimo incluso bajo fuertes condiciones de incertidumbre (aunque tendremos que especificar qué podemos entender por *óptimo* en estas condiciones), por lo que los **algoritmos** que buscamos para tomar decisiones tendrán como requisito ser **robustos frente a la incertidumbre**.
## Métodos
Existen muchos métodos para diseñar agentes inteligentes capaces de tomar decisiones. Dependiendo de la aplicación concreta que se esté abordando, de las características de su modelado, algunos métodos pueden ser más apropiados que otros. Difieren en las responsabilidades del diseñador y en las tareas que se dejan a la automatización.
Los métodos más comunes para abordar este diseño son:
1. **Programación explícita**. El método más directo, y más ingenuo, para diseñar un agente con capacidad de decisión es **anticipar todos los escenarios** en los que el agente podría encontrarse **y programar explícitamente la respuesta** que el agente debería dar a cada uno de ellos.
Este enfoque puede funcionar bien para problemas sencillos, pero supone una gran carga para el diseñador a la hora de proporcionar una estrategia completa y es difícil tener en cuenta la casuística combinada de eventos simultáneos.
Aunque se han propuesto varios lenguajes y marcos de programación de agentes para facilitar la programación de los mismos, todos ellos presentan limitaciones frente a problemas complejos del mundo real. Por ello, cada vez es más frecuente combinar la programación explícita en un marco especializado en agentes con cualquiera de los otros métodos.
1. **Aprendizaje supervisado**. En aquellos problemas en los que disponemos de suficiente casuística almacenada en forma de datos puede ser más fácil y provechoso mostrar a un agente lo que debe hacer que escribir un programa explícito que lo dirija. El diseñador proporciona un conjunto de ejemplos de entrenamiento que incluyen la acción ideal a tomar, y un **algoritmo de aprendizaje automático debe generalizar** a partir de estos ejemplos para seleccionar la acción óptima y responder ante situaciones novedosas (aunque cercanas a ejemplos presentes en el aprendizaje). Este enfoque se conoce como **aprendizaje supervisado** (en el contexto que estamos también se le denomina *clonación del comportamiento*), y funciona bien cuando un diseñador experto conoce realmente la elección de la mejor acción para una colección representativa de situaciones.
Aunque existe una gran variedad de algoritmos de aprendizaje supervisado, por lo general no suelen funcionar mejor que los diseñadores humanos en situaciones nuevas, pero sí permiten extraer un comportamiento automático óptimo en muchos casos en los que no se tienen ejemplos representativos, y facilita enormemente el diseño del agente cuando la casuística es variada.
En cierta forma, el algoritmo entrenado (llamado **modelo aprendido** en el entorno del aprendizaje) haría el papel del programa explícito del método anterior.
1. **Optimización**. Otro enfoque consiste en que el diseñador especifique el **espacio de posibles estrategias de decisión y una medida de rendimiento que debe maximizarse**. La evaluación del rendimiento de una estrategia de decisión suele implicar la ejecución de un lote de simulaciones. Por medio de la aplicación de un algoritmo de optimización, se realiza entonces una búsqueda de la estrategia óptima en este espacio.
Su validez y forma de optimización depende en gran medida de las condiciones del espacio (por ejemplo, de su tamaño, de si la medida de rendimiento no tiene muchos óptimos locales, etc.), lo que puede orientar acerca del método para encontrar el óptimo.
1. **Planificación**. La planificación es una forma de **optimización que utiliza un modelo de la dinámica del problema para ayudar a guiar la búsqueda del óptimo**. Una gran parte de la literatura explora diversos problemas de planificación, **habitualmente centrada en problemas deterministas**, que es una aproximación aceptable para algunos problemas porque permite utilizar métodos que pueden escalar más fácilmente a problemas de alta dimensión. Para otros problemas, sin embargo, es fundamental tener en cuenta la incertidumbre futura, que es el marco en el que nos queremos centrar.
1. **Aprendizaje por refuerzo**. El aprendizaje por refuerzo **relaja la suposición que se impone en la planificación de que se conoce un modelo de antemano**. En su lugar, la **estrategia de toma de decisiones se aprende mientras el agente interactúa con el entorno**. El diseñador proporciona una medida de rendimiento, y es el algoritmo de aprendizaje el que debe optimizar el comportamiento del agente.
Uno de los problemas más interesantes que surgen en el aprendizaje por refuerzo es que la elección de la acción no sólo afecta al éxito inmediato del agente en la consecución de sus objetivos, sino también a la capacidad del agente para aprender sobre el entorno e identificar las características del problema que puede explotar.
# Decisiones Secuenciales
Aunque es posible encontrar algunos problemas interesantes en el modelado de toma de decisiones de un paso, el caso más interesante es aquel en el que el agente no toma una única decisión, sino que ha de tomar una sucesión de decisiones secuenciales de las que depende el éxito o no del objetivo a cumplir.
Es decir, en la **toma de decisiones secuenciales** resolver un problema consiste en realizar acciones (tomar decisiones) de forma consecutiva y que aseguren la consecución de los objetivos planteados al agente. Debe tenerse en cuenta que la ejecución de cada una de las acciones puede conllevar un cambio dinámico en el propio entorno del problema (es decir, las acciones que se tomen en un momento afectarán al mundo y, consecuentemente, a las posibles acciones que se puedan tomar en el futuro y a las condiciones concretas del entorno de resolución).
Con este fin, vamos a presentar la aproximación más famosa para la resolución de este tipo de problema, un modelo conocido como **Procesos de Decisión de Markov** (MDP) para representar problemas de decisión secuenciales en los que los efectos de nuestras acciones son inciertos. Esta aproximación fue presentada originalmente por [R.E. Bellman](https://es.wikipedia.org/wiki/Richard_Bellman) en la década de los 50 (y publicada en su libro [_Dynamic Programming_](https://press.princeton.edu/books/paperback/9780691146683/dynamic-programming)).
## Elementos de la Toma de Decisiones Secuencial
Además del agente y el entorno, se pueden identificar cuatro elementos principales de un sistema de toma de decisiones secuencial (se debe tener en cuenta que esta organización es solo un modelo de representación, y no pretende reflejar una verdad universal del mundo real):
1. **Política**: define la forma de actuar del agente en un momento dado. A grandes rasgos, una política es un mapeo desde los estados percibidos del entorno hasta las acciones que se deben tomar cuando se encuentra ante cada estado. En algunos casos, una política puede darse por medio de una simple función o una tabla asociativa, mientras que en otros puede implicar un cálculo extenso, como podría ser un proceso de búsqueda y simulación. En general, las políticas no tienen porqué ser deterministas, sino que podrían ser estocásticas, especificando las probabilidades de cada acción.
1. **Señal de recompensa**: define el objetivo de la toma de decisiones. En cada paso de tiempo, el entorno envía al agente un único valor real llamado **recompensa**. La señal de recompensa define cuáles son los eventos *buenos* y *malos* para el agente, son las características inmediatas y definitorias del problema al que se enfrenta el agente. Obsérvese la simplificación impuesta al considerar que un solo valor numérico es suficiente para evaluar la bondad de un estado, que reduce el objetivo del agente a maximizar la recompensa total agregada que recibe a largo plazo.
La señal de recompensa es la base principal para modificar la política: si una acción seleccionada por la política va seguida de una baja recompensa, entonces la política puede intentar cambiarse para seleccionar en el futuro alguna otra acción más prometedora (que proporcione una mayor recompensa) en esa misma situación (aunque esta visión es tan cortoplacista como un algoritmo voraz de búsqueda de camino mínimo y, en general, no asegurará alcanzar el mejor resultado). En general, las señales de recompensa pueden ser funciones estocásticas del estado del entorno y de las acciones realizadas.
1. **Función de Valor**: Mientras que la señal de recompensa indica cómo de buena es la capacidad de decisión del agente en un sentido inmediato, una **función de valor** especifica su capacidad a largo plazo. A grandes rasgos, el valor de un estado es la cantidad total de recompensa que un agente puede esperar acumular en el futuro partiendo de ese estado y usando su política como medio de decisión.
1. **Modelo del Entorno**: Se trata de *algo* que *imita* el comportamiento del entorno o, más generalmente, que permite hacer inferencias sobre cómo se comportará el entorno. Por ejemplo, dado un estado y una acción, el modelo puede predecir el siguiente estado y la siguiente recompensa resultantes. Los modelos se utilizan para permitir una planificación por medio de *simulación*, es decir, cualquier forma de decidir un curso de acción teniendo en cuenta las posibles situaciones futuras antes de que se produzcan. Si disponemos de un modelo, podemos adelantarnos a la evolución del sistema e inferir más sencillamente en qué situación nos encontraríamos si realizáramos ciertas acciones sin necesidad de ejecutarlas (permite la previsión). Los métodos para resolver problemas de toma de decisiones que utilizan modelos del entorno y planificación se denominan **métodos basados en modelos**, en contraposición a los métodos más sencillos **sin modelos**, o **libres de modelos**, que son explícitamente aprendices de prueba y error, considerados casi lo contrario de la planificación.
## Procesos de Decisión de Markov
 En la mayoría de los casos los agentes habitan en un entorno cambiante, ya sea por la acción del propio agente o por acontecimientos externos (otros agentes, por ejemplo, si nos encontramos en un Sistema MultiAgente). Como hemos comentado, podemos pensar que el agente percibe el estado del mundo y luego realiza una acción que le lleva a un nuevo estado (que refleja cambios en el agente y/o en el entorno). Podemos hacer una suposición simplificadora adicional, y es que la elección del nuevo estado sólo depende del estado actual que percibe el agente y de su acción. Esta idea se recoge formalmente mediante lo que se conoce como **Proceso de Decisión de Markov** (**MDP**).
Un **Proceso de Desición de Markov** (MDP) es un proceso de control estocástico en tiempo discreto que se caracteriza por estados y resultados totalmente observables en los que influyen los responsables de la toma de decisiones. Satisface la **propiedad de Markov**, que establece que las decisiones tomadas en el paso de tiempo actual dependen de un número finito de pasos de tiempo anteriores (que puede reducirse a un solo paso). En algunos textos, se denomina **programa dinámico**, **programa dinámico estocástico**, **proceso de decisión secuencial** y **problema de control estocástico**.
!!!def:Proceso de Decisión de Markov
Un **Proceso de Decisión de Markov** (**MDP**) se define por la tupla $(S, A, T, R, γ)$, donde:
* $S$ representa el **conjunto de estados**, $s$, del entorno.
* $A$ representa el **conjunto de acciones**, $a$, que puede realizar un agente. En algunos estados, ciertas acciones no están permitidas, es decir, sólo se puede realizar un subconjunto de las acciones, denotado por $A_s$.
* $T$ representa la **función de transición**. $T(s'|s,a)$ indica la probabilidad de que el entorno pase al estado $s'$ desde el estado $s$ cuando un agente realiza la acción $a$.
* $R$ representa la **recompensa**. $R(s'|s,a)$ denota la recompensa recibida cuando se realiza la acción $a$ y el entorno pasa del estado $s$ al estado $s'$.
* $γ$ representa un **factor de descuento**, $γ ∈ [0, 1)$, que da más peso a la recompensa presente que a la recompensa futura.
El estado evoluciona de forma probabilística en función del estado actual y de la acción que realicemos. La suposición de que el siguiente estado depende sólo del estado y la acción actuales y no de ningún estado o acción anteriores se conoce como **propiedad o suposición de Markov**.
La función de transición $T(s'|s,a)$ da la probabilidad de que un agente en el estado $s$ que realiza la acción $a$ acabe en el estado $s'$. Para un mundo puramente **determinista**, fijado el par $(s,a)$, esta función será $0$ para todos los $s'$ excepto uno, para el que será $1$. Es decir, en un mundo determinista la acción de un agente tiene un efecto completamente predecible. En un entorno **no determinista** la acción de un agente podría conducir a un conjunto de estados diferentes, dependiendo del valor de esta función de probabilidad fija.
![Figura [MDP]: Ejemplo sencillo de MDP](img\sma1-1.png width="75%")
!!!Tip
La figura [MDP] muestra una representación de un **MDP**, en este caso, con $4$ estados, donde las acciones del agente están limitadas en función del estado. Por ejemplo, en el estado $s_1$ el agente sólo puede realizar las acciones $a_1$ y $a_2$. En este estado, si realiza la acción $a_1$ hay una probabilidad de $0.2$ de que se quede en el mismo estado, y de $0.8$ de que acabe en el estado $s_2$. Además, recibe una recompensa de $1$ sólo cuando llega a $s_3$, momento en el que su única opción es abandonar $s_3$ (por medio de las acciones $a_3$ o $a_4$).
En el ejemplo, la función de recompensa es una función determinista de $s$ y $a$ porque representa una expectativa, pero en general las recompensas pueden generarse estocásticamente en el entorno o incluso depender del siguiente estado resultante, como muestra la definición formal anterior.
Las recompensas en un MDP se tratan como componentes de una función de utilidad descompuesta aditivamente. En un problema de **horizonte finito** con $n$ decisiones, la **utilidad** asociada a una secuencia de recompensas $r_{1:n}$ ($r_{1:n}=\{r_i\}_{1\leq i\leq n}$) es, simplemente:
$$U=\sum_{t=1}^n r_t$$
La suma de recompensas se denomina a veces **rendimiento** o **rentabilidad**.
En un problema de **horizonte infinito** en el que el número de decisiones es ilimitado, la suma de recompensas puede llegar a ser infinita. En este caso, hay varias formas de definir la utilidad en términos de recompensas individuales, las más habitual es imponer el factor de descuento de la definición, $\gamma \in [0,1)$, y entonces la **utilidad** viene dada por:
$$U=\sum_{t=1}^\infty \gamma^{t-1}r_t$$
Este valor se denomina a veces **rentabilidad descontada**. Cuando $\gamma \in [0,1)$ y las recompensas están acotadas, la utilidad es finita. El factor de descuento hace que las recompensas en el presente valgan más que las recompensas en el futuro, un concepto que también aparece en economía.
Podemos representar un MDP en Julia usando la siguiente estructura de datos, que sigue completamente la formalización matemática que hemos dado, es decir: `(𝒮, 𝒜, T, R, γ)`.
~~~~Julia
struct MDP
𝒮 # state space
𝒜 # action space
T # transition function
R # reward function
γ # discount factor
end
~~~~
## Políticas y Funciones de Valor
!!!def:Políticas
Formalmente, una **política** es una función que determina qué acción seleccionar a partir de la historia pasada de estados y acciones. La acción a seleccionar en el momento $t$, dada la **historia** $h_t = (s_{1:t}, a_{1:t-1})$, se escribe $\pi_t(h_t)$.
Nosotros (y es lo más habitual) vamos a simplificar esta definición y consideraremos, en general, que una **política** es una función: $\pi:S\to A$, ya que como los estados y las recompensas futuras sólo dependen del estado y la acción actuales, podemos limitar nuestra atención a las políticas que sólo dependen del estado actual.
!!!def:Funciones de Valor y Políticas Óptimas
La **utilidad esperada** de ejecutar $\pi$ desde el estado $s$ se denota como $U^\pi(s)$. En el contexto de los MDP, $U^\pi$ se denomina también **función de valor** (se corresponde con la función de valor que vimos anteriormente).
Una **política óptima** $\pi^*$ es una política que maximiza la utilidad esperada o función de valor:
$$\pi^*(s)=\arg \max_\pi U^\pi(s),\ \forall s\in S$$
Dependiendo del modelo, puede haber múltiples políticas que sean óptimas. La función de valor asociada a una política óptima $\pi^*$ se denomina **función de valor óptima** y se denota como $U^*$.
Se puede encontrar una **política óptima** utilizando **programación dinámica**. En general, los algoritmos que utilizan programación dinámica para resolver MDPs son mucho más eficientes que los métodos de fuerza bruta.
## Evaluación de políticas
Antes de hablar de cómo calcular una política óptima, hablaremos de la **evaluación de la política**, donde calculamos la función de valor $U^\pi$ a partir de una política prefijada $\pi$.
La evaluación de la política puede hacerse de forma iterativa:
1. Si la política se ejecuta para un solo paso, la utilidad es $U^\pi(s) = R(s, \pi(s))$.
2. Los pasos posteriores pueden obtenerse a partir de la ecuación de **lookahead**, donde simplemente tenemos en cuenta la acumulación de utilidades esperadas a partir del recorrido que puede seguirse en el grafo de aplicación de acciones:
$$U^\pi_{k+1}(s) = R(s, \pi(s)) + \gamma \sum_{s'} T(s' | s, \pi(s))U^\pi_k(s')$$
Esta ecuación se implementa en los algoritmos 1 y 2.
La función de valor $U^\pi$ puede calcularse con una precisión arbitraria si se realizan suficientes iteraciones de la ecuación lookahead. La convergencia está garantizada porque, si $\gamma < 1$ y $R$ está acotada, la actualización en la ecuación es una contracción. En la convergencia se verifica la igualdad (basta tomar límites en ambos términos):
$$U^\pi(s) = R(s, \pi(s)) + \gamma \sum_{s'} T(s' | s, \pi(s))U^\pi(s')$$
a la que se denomina **ecuación de Bellman**.
!!!alg:Algoritmo 1.
Funciones para calcular el valor estado-acción de un estado `s` dada una acción `a` utilizando una estimación de la función de valor `U` para el MDP `𝒫`. La segunda versión maneja el caso cuando `U` es un vector.
~~~~Julia
function lookahead(𝒫::MDP, U, s, a)
𝒮, T, R, γ = 𝒫.𝒮, 𝒫.T, 𝒫.R, 𝒫.γ
return R(s,a) + γ*sum(T(s,a,s')*U(s') for s' in 𝒮)
end
~~~~
!!!alg: Algoritmo 2.
Evaluación iterativa de la política, que calcula iterativamente la función de valor para una política `π` para el MDP `𝒫` con espacios de estado y acción discretos utilizando `k_max` iteraciones.
~~~~Julia
function iterative_policy_evaluation(𝒫::MDP, π, k_max)
𝒮, T, R, γ = 𝒫.𝒮, 𝒫.T, 𝒫.R, 𝒫.γ
U = [0.0 for s in 𝒮]
for k in 1:k_max
U = [lookahead(𝒫, U, s, π(s)) for s in 𝒮]
end
return U
end
~~~~
Es interesante observar que, si $S$ es finito ($S=\{s_1,\dots,s_N\}$), entonces la evaluación de la política puede hacerse sin iteración resolviendo directamente el sistema de ecuaciones que refleja la ecuación de Bellman, ya que define un conjunto de $N$ ecuaciones lineales con $N$ incógnitas correspondientes a los valores de cada estado: $U^\pi(s_1),\dots,U^\pi(s_N)$. Una forma de resolver este sistema de ecuaciones es convertirlo primero a forma matricial:
$${\mathbf U}^\pi = {\mathbf R}^\pi + \gamma\mathbf{T}^\pi \mathbf{U}^\pi$$
donde ${\mathbf U}^\pi$ y ${\mathbf R}^\pi$ son las **funciones de utilidad y recompensa** representadas en forma vectorial con $N$ componentes. La matriz (de tamaño $N\times N$) $\mathbf{T}^\pi$ contiene las probabilidades de transición de los estados, donde $T^\pi_{ij}$ es la probabilidad de transición del estado $s_i$ al estado $s_j$.
La función de valor se obtiene como sigue:
$${\mathbf U}^\pi - \gamma{\mathbf T}^\pi{\mathbf U}^\pi = {\mathbf R}^\pi$$
$$({\mathbf I}- \gamma {\mathbf T}^\pi) {\mathbf U}^\pi = {\mathbf R}^\pi$$
$${\mathbf U}^\pi = ({\mathbf I} - \gamma {\mathbf T}^\pi)^{-1} {\mathbf R}^\pi$$
Este método se implementa en el algoritmo 3, y requiere $O(N^3)$ unidades de tiempo.
!!!alg: Algoritmo 3.
Evaluación exacta de una política, `π`, para un MDP, `𝒫`, con espacios de estado y acción discretos.
~~~~Julia
function policy_evaluation(𝒫::MDP, π)
𝒮, R, T, γ = 𝒫.𝒮, 𝒫.R, 𝒫.T, 𝒫.γ
R' = [R(s, π(s)) for s in 𝒮]
T' = [T(s, π(s), s') for s in 𝒮, s' in 𝒮]
return (I - γ*T')\R'
end
~~~~
## Políticas de la función de valor
La sección anterior mostraba cómo calcular una función de valor asociada a una política. Ahora vamos a mostrar cómo extraer una política a partir de una función de valor, que posteriormente utilizaremos para generar políticas óptimas.
Dada una función de valor $U$ (que puede corresponderse o no a la función de valor óptima), podemos construir una política $\pi$ que maximice la ecuación de lookahead introducida anteriormente:
$$\pi(s) = \arg \max_a \Big( R(s, a) + \gamma \sum_{s'} T(s' | s, a) U(s') \Big)$$
Nos referimos a esta política como una **política voraz** con respecto a $s$, ya que se preocupa de optimizar la política considerando solo un paso adelante. Si $U$ es la función de valor óptima, entonces la política extraída es óptima. El algoritmo 4 implementa esta idea.
!!!alg:Algoritmo 4.
Una política de función de valor extraída de una función de valor `U` para un MDP `𝒫`. La función voraz se utilizará en otros algoritmos.
~~~~Julia
struct ValueFunctionPolicy
𝒫 # problem
U # utility function
end
function greedy(𝒫::MDP, U, s)
u, a = findmax(a->lookahead(𝒫, U, s, a), 𝒫.𝒜)
return (a=a, u=u)
end
(π::ValueFunctionPolicy)(s) = greedy(π.𝒫, π.U, s).a
~~~~
!!!def:$Q$-función
Una forma alternativa de representar una política es utilizar la **función de valor de la acción**, a veces llamada **$Q$-función**, que representa el rendimiento esperado cuando se empieza en el estado $s$, se toma la acción $a$, y luego se continúa con la política voraz con respecto a $Q$:
$$Q(s, a) = R(s, a) + \gamma \sum_{s'} T(s' | s, a) U(s')$$
A partir de esta función de valor de la acción, podemos obtener la función de valor,
$$U(s) = \max_a Q(s, a)$$
así como la política,
$$\pi(s) = \arg \max_a Q(s, a)$$
Almacenar $Q$ explícitamente para problemas discretos requiere $O(|S| \times |A|)$ de almacenamiento en lugar de $O(|S|)$ para $U$, pero no tenemos que usar $R$ y $T$ para extraer la política.
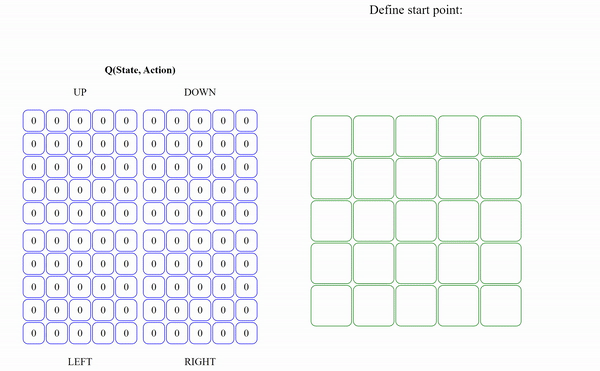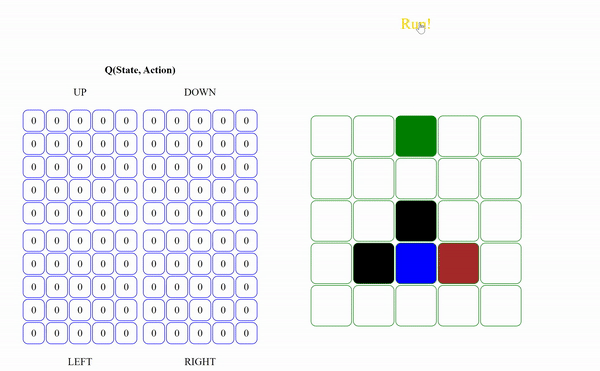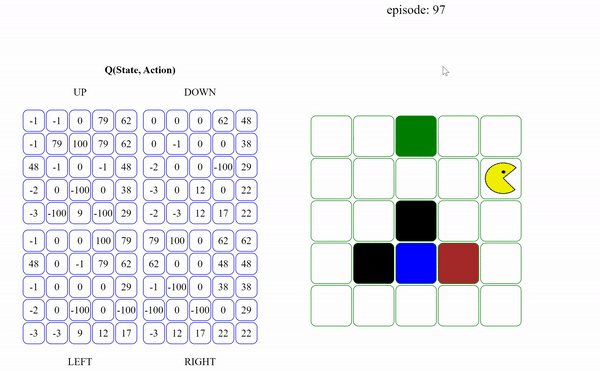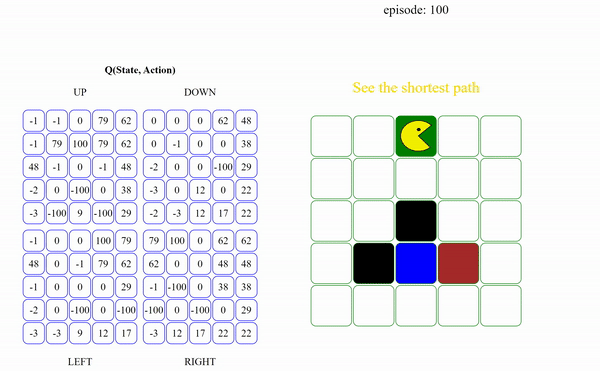
## Iteración de la Política
La **iteración de la política** (algoritmo 5) es una forma de calcular una política óptima. Consiste en iterar entre la evaluación de la política que vimos anteriormente y la mejora de la política mediante una política voraz (algoritmo 4). Se garantiza que la iteración de la política converge para cualquier política inicial, y en un número finito de iteraciones cuando hay un número finito de políticas, y además cada iteración mejora la política si puede ser mejorada. Aunque el número de políticas posibles es exponencial en el número de estados, la iteración de políticas suele converger rápidamente.
!!!alg:Algoritmo 5.
La iteración de políticas, que mejora iterativamente una política inicial `π` para obtener una política óptima para un MDP `𝒫` con espacios de estado y acción discretos.
~~~~Julia
struct PolicyIteration
π # initial policy
k_max # maximum number of iterations
end
function solve(M::PolicyIteration, 𝒫::MDP)
π, 𝒮 = M.π, 𝒫.𝒮
for k = 1:M.k_max
U = policy_evaluation(𝒫, π)
π′ = ValueFunctionPolicy(𝒫, U)
if all(π(s) == π′(s) for s in 𝒮)
break
end
π = π′
end
return π
end
~~~~
La iteración de políticas tiende a ser costosa porque debemos evaluar la política en cada iteración. Una variación de la iteración de políticas, llamada **iteración de políticas modificada**, aproxima la función de valor utilizando una evaluación de políticas iterativa (`iterative_policy_evaluation`) en lugar de una evaluación de políticas exacta. Podemos elegir el número de iteraciones de evaluación de la política entre los pasos de mejora de la política. Si utilizamos sólo una iteración entre pasos, este enfoque es idéntico a la iteración de valores.
## Iteración del Valor
La **iteración del valor** es una alternativa a la iteración de la política que se utiliza a menudo debido a su simplicidad. A diferencia de la mejora de la política, la iteración del valor actualiza la función de valor directamente. Comienza con cualquier función de valor $U$ acotada. Una inicialización común es $U(s) = 0$ para todo $s$.
La función de valor puede mejorarse aplicando la actualización de Bellman:
$$U_{k+1}(s) = \max_a \Big( R(s, a) + \gamma \sum_{s'} T(s' | s, a) U_k(s') \Big)$$
Este procedimiento se implementa en el algoritmo 6.
!!!alg: Algoritmo 6
El procedimiento de actualización aplicado a un MDP `𝒫`, que mejora una función de valor `U` en el estado `s`.
~~~~Julia
function backup(𝒫::MDP, U, s)
return maximum(lookahead(𝒫, U, s, a) for a in 𝒫.𝒜)
end
~~~~
La aplicación repetida de esta actualización garantiza la convergencia a la función de valor óptima. Al igual que la evaluación iterativa de políticas, podemos utilizar el hecho de que la actualización es contractiva para demostrar la convergencia. Se garantiza que esta política óptima satisface la ecuación de optimalidad de Bellman:
$$U^*(s) = \max_a \Big( R(s, a) + \gamma \sum_{s'} T(s' | s, a) U^*(s') \Big)$$
Se puede extraer una política óptima de $U^*$ de forma similar a como vimos antes. La iteración del valor se implementa en el algoritmo 7.
!!!alg:Algoritmo 7.
Iteración del valor, que mejora iterativamente una función de valor `U` para obtener una política óptima para un MDP `𝒫` con espacios de estado y acción discretos. El método termina después de `k_max` iteraciones.
~~~~Julia
struct ValueIteration
k_max # maximum number of iterations
end
function solve(M::ValueIteration, 𝒫::MDP)
U = [0.0 for s in 𝒫.𝒮]
for k = 1:M.k_max
U = [backup(𝒫, U, s) for s in 𝒫.𝒮]
end
return ValueFunctionPolicy(𝒫, U)
end
~~~~
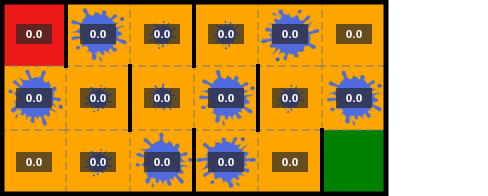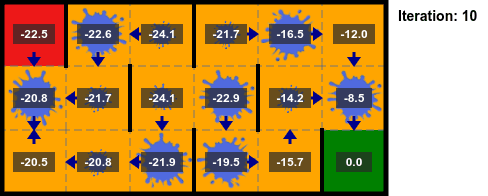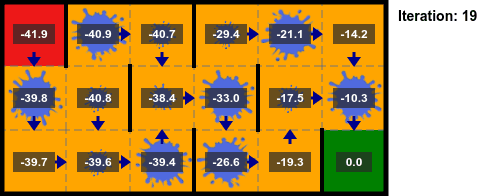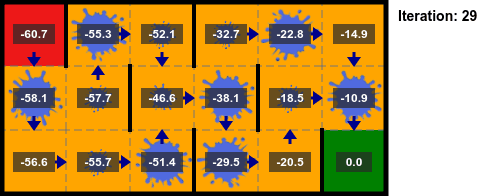
La implementación en el algoritmo 7 se detiene después de un número fijo de iteraciones, pero también es común terminar las iteraciones antes de tiempo sobre la base del cambio máximo en el valor $||U_{k+1} - U_k||_\infty$, llamado el **residuo de Bellman**. Si el residuo de Bellman cae por debajo de un umbral $\delta$, las iteraciones terminan. Un residuo de Bellman de $\delta$ garantiza que $||U_k - U^*||_\infty < \epsilon=\delta \gamma/(1 - \gamma)$. Si $\gamma$ es cercano a $1$, la convergencia es más lenta, si $\gamma$ es más cercano a $0$, entonces no necesitamos realizar tantas iteraciones.
Conocer la desviación máxima de la función de valor estimada respecto a la función de valor óptima, $|| U_k - U^*||_\infty < \epsilon$, nos permite acotar la desviación máxima de la recompensa obtenida bajo la política extraída $\pi$ respecto a una política óptima $\pi^*$. Esta pérdida de política $||U^\pi - U^*||_\infty$ está acotada por $2\epsilon\gamma/(1-\gamma)$.
## Iteración asíncrona del valor
La iteración del valor tiende a ser computacionalmente intensiva, ya que cada entrada de la función de valor $U_k$ se actualiza en cada iteración para obtener $U_{k+1}$. En la **iteración de valor asíncrona**, sólo se actualiza un subconjunto de estados en cada iteración. La iteración de valor asíncrona sigue garantizando la convergencia a la función de valor óptima, siempre que cada estado se actualice un número infinito de veces.
Un método común de iteración de valor asíncrono, la **iteración de valor Gauss-Seidel** (algoritmo 8), hace un barrido a través de un ordenamiento de los estados y aplica la actualización de Bellman en su lugar:
$$U(s) \leftarrow \max_a \Big( R(s, a) + \gamma \sum_{s'} T(s' | s, a) U(s')\Big)$$
El ahorro computacional reside en no tener que construir una segunda función de valor en memoria con cada iteración. La iteración de valor de Gauss-Seidel puede converger más rápidamente que la iteración de valor estándar, dependiendo del orden elegido. En algunos problemas, el estado contiene un índice de tiempo que se incrementa de forma determinista hacia adelante en el tiempo. Si aplicamos la iteración de valor de Gauss-Seidel empezando por el último índice de tiempo y trabajando hacia atrás, este proceso se llama a veces **iteración de valor de inducción hacia atrás**.
!!!alg:Algoritmo 8: Iteración Asíncrona de Valores.
Actualiza los estados de una manera diferente a la iteración de valores, a menudo ahorrando tiempo de cálculo. El método termina después de `k_max` iteraciones.
~~~~Julia
struct GaussSeidelValueIteration
k_max # maximum number of iterations
end
function solve(M::GaussSeidelValueIteration, 𝒫::MDP)
U = [0.0 for s in 𝒫.𝒮]
for k = 1:M.k_max
for (i, s) in enumerate(𝒫.𝒮)
U[i] = backup(𝒫, U, s)
end
end
return ValueFunctionPolicy(𝒫, U)
end
~~~~
# Aprendizaje por Refuerzo
Hasta hasta ahora, hemos asumido que los modelos de transición y recompensa son conocidos. En muchos problemas, sin embargo, estos modelos no se conocen con exactitud, y el agente debe aprender a actuar a través de la experiencia: observando los resultados de sus acciones en forma de transiciones de estado y recompensas, el agente debe elegir acciones que maximicen su acumulación de recompensas a largo plazo.
!!!Note
La resolución de este tipo de problemas en los que existe *incertidumbre sobre el modelo* es el objeto de estudio concreto del campo del **Aprendizaje por Refuerzo** (RL). Así pues, RL es un caso particular del campo más general de Toma de Decisiones Bajo Incertidumbre (de hecho, últimamente se pueden encontrar muchas referencias en las que se denomina RL al campo general).
En esta parte del módulo vamos a intentar dar algunas notas acerca de cómo abordar el problema de la toma de decisiones cuando hay incertidumbre sobre el modelo:
1. En primer lugar, para poder conocer cómo funciona el mundo, el agente debe equilibrar cuidadosamente la **exploración** del entorno con la **explotación** del conocimiento adquirido a través de las experiencias anteriores (o incluso haciendo uso de experiencias ajenas, como ocurre en la variante de *clonación del comportamiento*).
2. En segundo lugar, debemos tener presente que las recompensas pueden recibirse mucho después de que se hayan tomado las decisiones importantes, por lo que el crédito de las recompensas posteriores debe asignarse a las decisiones anteriores de forma adecuada para que se *refuercen* las acciones correctas, y no todas aquellas que simplemente han tenido lugar durante la trayectoria llevada a cabo por el agente (por ello, surgen muchos estudios que analizan las trayectorias para reforzar las secciones más adecuadas).
3. En tercer lugar, el agente debe generalizar a partir de una experiencia limitada, lo que le lleva a la necesidad de ser capaz de generalizar teniendo presente que puede haber muchas partes no exploradas del problema, e incluso muchas opciones de acción no consideradas en aquellas partes que sí ha podido explorar.
Los agentes de aprendizaje por refuerzo deben equilibrar la exploración del entorno con permitir que el agente construya un modelo completo, pero es probable que tengan que sacrificar la obtención de recompensas. La explotación pura hace que el agente elija continuamente la acción que considera mejor para acumular recompensa, pero puede haber otras acciones mejores que podrían llevarse a cabo y que el agente no llega a conocer si no explora el espacio.
En este punto, el aprendizaje por refuerzo puede tener dos orientaciones principales:
1. Reconstruir un modelo de $T$ y $R$ que le permitan ejecutar las aproximaciones vistas en los apartados anteriores.
2. Evitar esta reconstrucción, y ver si hay algún mecanismo para optimizar la recompensa final sin necesidad de pasar por este aprendizaje intermedio de forma explícita.
Vamos a centrarnos en el aprendizaje por refuerzo sin modelos, que no busca construir representaciones explícitas de los modelos de transición y recompensa, sino que modelan la función de valor de la acción directamente. Evitar representaciones explícitas es atractivo, especialmente cuando el problema tiene una dimensión muy alta. Comenzaremos introduciendo la estimación incremental de la media de una distribución, que desempeña un papel importante en la estimación de la media de los rendimientos, para luego ver algunos algoritmos comunes libres de modelos y métodos para manejar la recompensa retardada de manera más eficiente.
!!!Note
Aunque el aprendizaje por refuerzo se ha centrado en problemas en los que se desconoce el modelo del entorno, también se utiliza a menudo para problemas con modelos conocidos. Los métodos libres de modelo que veremos pueden ser especialmente útiles en entornos complejos como una forma de programación dinámica aproximada. Pueden utilizarse para producir políticas en diferido (*offline*), o como medio para generar la siguiente acción en un contexto en tiempo real (*online*).
## Estimación Incremental de la Media
Muchos métodos libres de modelo estiman incrementalmente la función de valor de la acción $Q(s, a)$ a partir de muestras. Por ello, veremos genéricamente cómo se puede modelar la estimación incremental de una variable cualquiera $X$ a partir de $m$ muestras, $x^{(1)},\dots,x^{(m)}$:
$$\hat{x}_m = \frac{1}{m} \sum_{i=1}^m x^{(i)}$$
Podemos derivar la actualización incremental:
$$\hat{x}_m = \frac{1}{m} \Big( x^{(m)} + \sum_{i=1}^{m−1} x^{(i)}\Big)=\frac{1}{m}\Big(x^{(m)} + (m − 1) \hat{x}_{m−1}\Big)=\hat{x}_{m−1} + \frac{1}{m} \Big(x^{(m)} − \hat{x}_{m−1}\Big)$$
Podemos reescribir esta ecuación con la introducción de una función de ratio de aprendizaje $\alpha_m$:
$$\hat{x}_m = \hat{x}_{m−1} + \alpha_m \Big(x^{(m)} − \hat{x}_{m−1}\Big)$$
La tasa de aprendizaje puede ser una función distinta de $1/m$. Para garantizar la convergencia, generalmente seleccionamos $\alpha_m$ de forma que tengamos $\displaystyle{\sum_{m=1}^\infty}\alpha_m = \infty$ y $\displaystyle{\sum_{m=1}^\infty} \alpha_m^2 < \infty$. La primera condición garantiza que los pasos sean suficientemente grandes, y la segunda, que sean suficientemente pequeños.
Si la tasa de aprendizaje es constante, lo que es común en aplicaciones de aprendizaje por refuerzo, entonces los pesos de las muestras más antiguas decaen exponencialmente con una tasa de $(1 - \alpha)$. Con una tasa de aprendizaje constante, podemos actualizar nuestra estimación después de observar $x$ utilizando la siguiente regla:
$$\hat{x}\leftarrow \hat{x} + \alpha(x − \hat{x})$$
## Q-Learning
El algoritmo **Q-Learning** se basa en la aplicación de una estimación incremental de la función de valor de acción $Q(s, a)$. La actualización se deriva de la forma de valor de acción de la ecuación de expectativas de Bellman:
$$Q(s, a) = R(s, a) + \gamma \sum_{s'} T(s' | s, a) U(s') = R(s, a) + \gamma \sum_{s'} T(s' | s, a) \max_{a'} Q(s', a')$$
En lugar de utilizar $T$ y $R$, podemos reescribir la ecuación anterior en términos de una expectativa sobre muestras de recompensa $r$ y el siguiente estado $s'$:
$$Q(s, a) = \mathbb{E}_{r,s'}[r + \gamma \max_{a'} Q(s', a')]$$
Si usamos la estimación incremental de la media (esperanza) podemos producir una regla de actualización incremental para estimar la función de valor de acción:
$$Q(s, a) \leftarrow Q(s, a) + \alpha \Big( r + \gamma \max_{a'} Q(s', a') − Q(s, a)\Big)$$
Nuestra elección de acciones afecta a los estados en los que terminamos y, por tanto, a nuestra capacidad para estimar $Q(s, a)$ con precisión. Para garantizar la convergencia de nuestra función de valor de acción, necesitamos adoptar alguna forma de política de exploración, como $\epsilon$-voraz, al igual que hicimos para los métodos basados en modelos.
!!!Alg: Q- Learning
~~~~~~C
mutable struct QLearning
𝒮 # state space (assumes 1:nstates)
𝒜 # action space (assumes 1:nactions)
γ # discount
Q # action value function
α # learning rate
end
function update!(model::QLearning, s, a, r, s′)
γ, Q, α = model.γ, model.Q, model.α
Q[s,a] += α*(r + γ*maximum(Q[s′,:]) - Q[s,a])
return model
end
~~~~~~

## Sarsa
**Sarsa** es una alternativa a Q-Learning. Su nombre se debe a que utiliza $(s, a, r, s', a')$ para actualizar la función $Q$ en cada paso. Utiliza la siguiente acción $a'$ para actualizar $Q$, en lugar de maximizar sobre todas las acciones posibles:
$$Q(s, a) \leftarrow Q(s, a) + \alpha \Big( r + \gamma Q(s', a' ) − Q(s, a)\Big)$$
Con una estrategia de exploración adecuada, $a'$ convergerá a $\arg \max_{a'} Q(s', a')$, que es lo que se utiliza en Q-Learning.
Este cambio hace que ambos métodos se clasifiquen de forma muy distinta: Sarsa es un método de aprendizaje por refuerzo basado en políticas, porque intenta estimar directamente el valor de la política de exploración mientras la sigue; y Q-Learning es un método no basado en políticas, porque intenta encontrar el valor de la política óptima mientras sigue la estrategia de exploración. Aunque tanto Q-learning como Sarsa convergen a una estrategia óptima, la velocidad de convergencia depende de la aplicación.
!!!Alg: Sarsa
~~~~~~C
mutable struct Sarsa
𝒮 # state space (assumes 1:nstates)
𝒜 # action space (assumes 1:nactions)
γ # discount
Q # action value function
α # learning rate
ℓ # most recent experience tuple (s,a,r)
end
function update!(model::Sarsa, s, a, r, s′)
if model.ℓ != nothing
γ, Q, α, ℓ = model.γ, model.Q, model.α, model.ℓ
model.Q[ℓ.s,ℓ.a] += α*(ℓ.r + γ*Q[s,a] - Q[ℓ.s,ℓ.a])
end
model.ℓ = (s=s, a=a, r=r)
return model
end
~~~~~~
En el algoritmo, actualizamos la matriz `Q` que contiene los valores estado-acción, `α` es una tasa de aprendizaje constante, y `ℓ` es la tupla de experiencia más reciente.
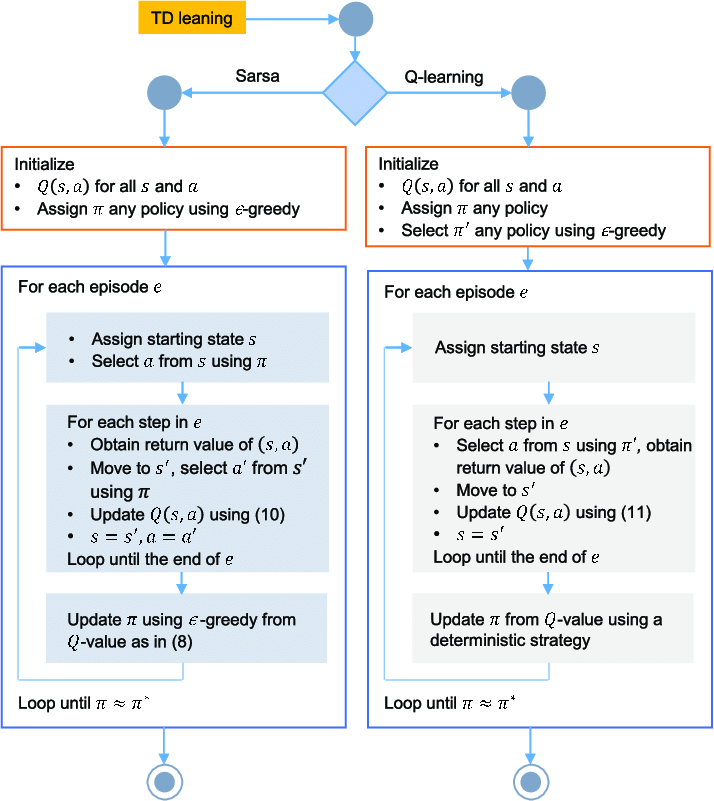
La diferencia existente entre SARSA y Q-Learning se explicita gráficamente en el siguiente diagrama:

Lo que da lugar a la diferente implementación que se aprecia entre ellos:
# ML en la Toma de Decisiones
Uno de los problemas más importantes que encontramos con las aproximaciones vistas radica en las estructuras de datos que hemos de manipular para poder actualizar los valores asociados a las diversas funciones que calculamos ($U$, $Q$, $\pi$,...). En general, el número de entradas que hemos de considerar son del orden de $|S|$ o $|S| \times |A|$, que en los problemas interesantes se hace intratable (o, directamente, imposibles, como cuando trabajamos con espacios de estados/acciones continuos). Al fin y al cabo, el problema radica en nuestra aproximación, que estamos intentando representar funciones a partir de tablas de asociación (arrays, diccionarios, etc.).
Pero a lo largo del máster hemos encontrado métodos alternativos para aproximar estas funciones de forma mucho más compacta y eficiente: el **Aprendizaje Automático**, en general, y las **Redes Neuronales**, en particular.
Grosso modo, el objetivo del aprendizaje automático es precisamente ese, dar aproximaciones de funciones de forma genérica presuponiendo algún tipo de estructura básica en forma de funciones de hipótesis (una generalización computacional a lo que se hace desde hace tiempo en el aprendizaje estadístico). Así visto, si representamos adecuadamente los datos que usa el agente para su toma de decisiones (el estado actual, en su forma más simple, o la trayectoria de estados/acciones/recompensas de varios pasos de ejecución, en su forma más completa), podríamos utilizar modelos de aprendizaje para aproximar las diversas funciones que, iterativamente, aproximan el conocimiento completo que requiere para una correcta toma de decisiones.

El uso de modelos de ML para aproximar este comportamiento se remonta a varios años pero, recientemente, la aparición del Deep Learning ha multiplicado en varios órdenes de magnitud la capacidad de aproximación de entornos complejos, permitiendo que una sola red aproxime simultáneamente $U$, $Q$ y $\pi$, aprovechando que todas ellas hacen uso de las mismas entradas y son realmente distintas mediciones del mismo proceso. El uso conjunto de DL y RL es lo que se ha denominado **Deep Reinforcement Learning**.
