**SVRAI**
Problemas de Satisfacción de Restricciones
Definiciones y Métodos
# Introducción
En muchas ocasiones la resolución de problemas está sujeta a que las diversas unidades en las que se pueden descomponer verifiquen ciertos conjuntos de restricciones. Problemas tan cotidianos como fijar una cita con unos amigos, comprar un coche, o preparar una receta de cocina pueden depender de muchos aspectos interdependientes, e incluso conflictivos, sujetos a un conjunto de **restricciones** que deben ser satisfechas para poder encontrar una solución al problema planteado.
Históricamente, la representación y resolución de **problemas de satisfacción de restricciones** (**PSR**, por sus siglas en español, **CSP**, por sus siglas en inglés) ha generado una gran expectación entre expertos de muchas áreas debido a su potencial para la resolución de grandes problemas reales que caen, en muchas ocasiones, dentro de lo que se conocen como problemas **NP** (aquellos que presentan una complejidad computacional superior para su resolución). Los primeros trabajos relacionados con la programación de restricciones datan de los años 60 y 70 en el campo de la Inteligencia Artificial, aunque sus técnicas se han desarrollado desde mucho antes en diversas áreas de las Matemáticas y con aplicaciones a Economía, Ingeniería, Física, etc.
!!!
La idea de CSP es representar problemas mediante la declaración de restricciones sobre el área del problema (el espacio de posibles soluciones) y consecuentemente encontrar soluciones factibles que satisfagan todas las restricciones. A veces, se buscan soluciones que, además, optimicen algunos criterios determinados, en cuyo caso decimos que es un **Problema de Optimización de Restricciones** (**COP**, por sus siglas en inglés).
La resolución de problemas con restricciones puede dividirse en dos ramas claramente diferenciadas, donde se aplican metodologías fundamentalmente distintas:
1. aquella que trata con problemas con **dominios finitos**, y
2. la que trata problemas sobre **dominios infinitos** o dominios más complejos.
En esta ocasión nos centraremos principalmente en problemas con dominios finitos, que básicamente consisten en un conjunto finito de variables, un dominio de valores finito para cada variable y un conjunto de restricciones que acotan las posibles combinaciones de valores que estas variables pueden tomar en su dominio.
!!!Tip:Ejemplo
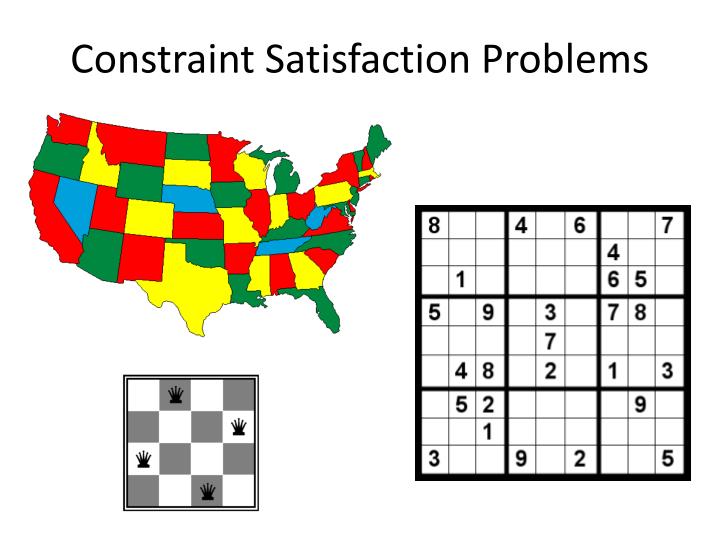
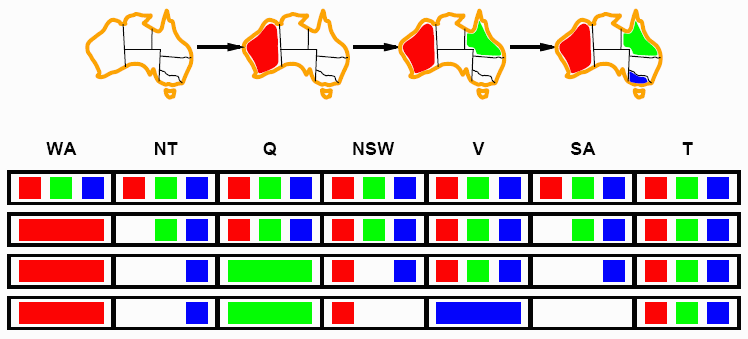
 El **problema de coloración de mapas** es un problema clásico que se puede formular como un CSP. En este problema tenemos un conjunto de colores y un mapa dividido en regiones, y el objetivo es colorear cada región del mapa de manera que regiones adyacentes tengan distintos colores. Una forma de modelar este problema dentro del CSP sería asociando una variable a cada región del mapa, el dominio de cada variable sería el conjunto de posibles colores disponibles, y para cada par de regiones contiguas añadir una restricción sobre los valores de las variables correspondientes que impida asignarles el mismo valor (color). Como suele ser habitual, este mapa puede ser representado mediante un grafo donde los nodos representan las diversas regiones del mapa y cada par de regiones adyacentes están unidas por una arista. Veremos que esta representación en forma de grafo, que en este problema es natural, será usada como metodología general para dar una estructura a las restricciones de cualquier CSP.
# Metodología para resolver CSP
!!!Def
Como es habitual con los sistemas de representación, la resolución de un CSP consta de dos fases, que son:
1. **Modelar/Representar el problema como un problema de satisfacción de restricciones**. Para ello, y siguiendo una metodología similar al ejemplo anterior, el problema se expresa mediante un conjunto de variables, dominios en los que toman los posibles valores, y restricciones sobre estas variables.
2. **Procesar las restricciones**. Una vez formulado el problema como un CSP, hay dos maneras de procesar las restricciones:
- **Técnicas de consistencia**: basadas en la eliminación de valores inconsistentes de los dominios de las variables (es decir, que no verifican las restricciones impuestas). A veces se pueden aplicar aquí técnicas derivadas de la [Lógica Proposicional](http://www.cs.us.es/~fsancho/?e=120) (o de primer orden).
- **Algoritmos de búsqueda**: se basan en la exploración sistemática del espacio de soluciones hasta encontrar una solución (o probar que no existe tal solución en caso contrario) que verifica todas las restricciones del problema.
Lo más normal es que se combinen ambas aproximaciones, ya que las técnicas de consistencia permiten deducir información del problema y reducir el espacio de soluciones para poder explorarlo usando algoritmos de búsqueda más o menos tradicionales.
## Modelización/Representación del CSP
La etapa fundamental para la resolución de problemas por medio de CSP es el modelado del problema en términos de **variables**, **dominios** y **restricciones**.
Como intentar dar una formalización completa de este proceso puede ser un poco engorroso, y sin embargo es bastante natural el proceso que se lleva a cabo, vamos a presentar esta etapa de modelado por medio de un ejemplo en el que se mostrarán diversas modelizaciones de un mismo problema y se pondrán de manifiesto las ventajas de una modelización adecuada para resolverlo.
!!!Tip: Ejemplo
Consideremos el conocido **problema criptoaritmético ’send+more=money’**. Este problema puede ser declarado como: asignar a cada letra $\{s, e, n, d, m, o, r, y\}$ un dígito diferente del conjunto $\{0,...,9\}$ de forma que se satisfaga la expresión $send+more=money$.

La manera más directa de modelar este problema es asignando una variable a cada una de las letras (que vendrán representadas por las mismas letras), todas ellas tomando valores en el dominio $\{0,...,9\}$ y con las restricciones de:
1. Todas las variables toman valores distintos, y
2. Se satisface $send+more=money$.
De esta forma, podemos escribir las restricciones como:
$$10^3 (s+m)+10^2 (e+o)+10(n+r)+d+e = 10^4 m + 10^3 o + 10^2 n + 10e + y$$
$$s\neq e,\ s\neq n,\ ...,\ r\neq y$$
Esta representación del problema es correcta, pero no es muy útil, ya que la primera de las restricciones exige manipular todas las variables simultáneamente y no facilita recorrer el espacio combinatorio de valores de una forma cómoda (ten en cuenta siempre que, finalmente, vamos a recorrer este espacio de combinaciones de valores como un espacio de estados, como veremos en el siguiente tema). Por lo que, al no disponer de restricciones locales entre las variables, no podemos podar el espacio de búsqueda para agilizar la búsqueda de soluciones.
Vamos a dar otro modelado similar pero más eficiente para resolver el problema, que consiste en decomponer esta restricción global en restricciones más pequeñas haciendo uso de las relaciones que se producen entre los dígitos que ocupan la misma posición en una suma. Para ello, introducimos los **dígitos de acarreo** para descomponer la ecuación anterior en una colección de pequeñas restricciones.
!!!Tip:Otra representación

Tal y como está planteado el problema, $m$ debe de tomar el valor $1$ (ya que es el acarreo de 2 cifras que como mucho pueden sumar $18$, más un posible acarreo previo de una unidad, lo que limita el resultado a $19$) y por lo tanto $s$ solamente puede tomar valores de $\{1,...,9\}$ (si $s=0$ entonces no podría haber acarreo). Además de las variables del modelo anterior, el nuevo modelo incluye tres variables adicionales, $c_1$, $c_2$, $c_3$ que sirven como dígitos de acarreo. Aunque introducimos nuevas variables, por lo que el espacio de búsqueda se amplia, éstas nos permitirán simplificar las restricciones y facilitar su exploración de forma considerable. En consecuencia, el dominio de $s$ es $\{1,...,9\}$, el dominio de $m$ es $\{1\}$, el dominio de los dígitos de acarreo es $\{0,1\}$, y el dominio del resto de variables es $\{0,...,9\}$.
Con la ayuda de los dígitos de acarreo la restricción de la ecuación anterior puede descomponerse en varias restricciones más pequeñas (junto con las restricciones que indican que todas las variables originales son distintas entre sí):
$$e + d = y + 10c_1$$
$$c_1 + n + r = e + 10c_2$$
$$c_2 + e + o = n + 10c_3$$
$$c_3 + s + m = 10m + o$$
Esta nueva representación presenta la ventaja de que las restricciones más pequeñas pueden comprobarse durante la búsqueda de una forma más sencilla y local, permitiendo podar más inconsistencias y consecuentemente reduciendo el tamaño del espacio de búsqueda efectivo.
# Formalización de CSP
Vamos a presentar más formalmente los conceptos y objetivos básicos que son necesarios en los problemas de satisfacción de restricciones y que utilizaremos a lo largo de esta entrada.
**Definición.** Un **problema de satisfacción de restricciones** (**CSP**) es una terna $(X,D,C)$ donde:
1. $X$ es un conjunto de $n$ variables $\{x_1 ,...,x_n \}$.
2. $D =\langle D_1 ,...,D_n \rangle$ es un vector de dominios ($D_i$ es el dominio que contiene todos los posibles valores que puede tomar la variable $x_i$).
3. $C$ es un conjunto finito de restricciones. Cada restricción está definida sobre un conjunto de $k$ variables por medio de un predicado que restringe los valores que las variables pueden tomar simultáneamente.
Una **asignación de variables**, $(x,a)$, es un par *variable-valor* que representa la asignación del valor $a$ a la variable $x$. Una asignación de un conjunto de variables es una tupla de pares ordenados, $((x_1 ,a_1 ),...,(x_i ,a_i ))$, donde cada par ordenado $(x_i,a_i)$ asigna el valor $a_i$ a la variable $x_i$. Una tupla se dice **localmente consistente** si satisface todas las restricciones formadas por variables de la tupla.
Una **solución a un CSP** es una asignación de valores a todas las variables de forma que se satisfagan todas las restricciones. Es decir, una solución es una tupla consistente que contiene todas las variables del problema. Una **solución parcial** es una tupla consistente que contiene algunas de las variables del problema. Diremos que un **problema es consistente**, si existe al menos una solución.
Observa la similitud con las definiciones de satisfactibilidad, modelo, etc. de la Lógica Proposicional.
Básicamente, los objetivos que deseamos alcanzar se centran en una de las siguientes opciones:
1. Encontrar una solución, sin preferencia alguna.
2. Encontrar todas las soluciones.
3. Encontrar una solución *óptima* (dando alguna **función objetivo** definida en términos de las variables).

Antes de entrar con más detalles vamos a resumir la notación que utilizaremos posteriormente:
* **Variables**: Para representar las **variables** utilizaremos las últimas letras del alfabeto, por ejemplo $x,y,z$, así como esas mismas letras con un subíndice.
* **Restricciones**: La **aridad** de una restricción es el número de variables que intervienen en dicha restricción. Una **restricción unaria** es una restricción que consta de una sola variable. Una **restricción binaria** es una restricción que consta de dos variables. Una **restricción n−aria** es una restricción que involucra a $n$ variables. Una **restricción k−aria** entre las variables $\{x_1 ,...,x_k\}$ la denotaremos por $C_{1..k}$. De esta manera, una **restricción binaria** entre las variables $x_i$ y $x_j$ la denotaremos por $C_{ij}$. Cuando los índices de las variables en una restricción no son relevantes, lo denotaremos simplemente por $C$.
!!!Tip:Ejemplo
La restricción $x \leq 5$ es una restricción unaria sobre la variable $x$. La restricción $x_4 − x_3 \neq 3$ es una restricción binaria. La restricción $2x_1 − x_2 + 4x_3 \leq 4$ es una restricción ternaria.
!!!Def
Una tupla de una restricción $C_{i..k}$ es un elemento del producto cartesiano $D_i \times \dots\times D_k$. Una tupla que satisface la restricción $C_{i..k}$ se le llama **tupla permitida o válida**. Una tupla de una restricción $C_{i..k}$ se dice que es **soporte** para un valor $a \in D_j$ si la variable $x_j \in X_{C_{i..k} }$, es una tupla permitida y contiene a $(x_j,a)$. Verificar si una tupla dada es permitida o no por una restricción se llama **comprobación de la consistencia**.
Una restricción puede definirse extensionalmente mediante un conjunto de tuplas válidas o no válidas (cuando sea posible) o también intensionalmente mediante un predicado entre las variables.
!!!Tip:Ejemplo
Consideremos una restricción entre 4 variables $x_1 ,x_2 ,x_3 ,x_4$ , todas ellas con dominios el conjunto $\{1,2\}$, donde la suma entre las variables $x_1$ y $x_2$ es menor o igual que la suma entre $x_3$ y $x_4$. Esta restricción puede representarse intencionalmente mediante la expresión $x_1 + x_2 \leq x_3 + x_4$. Además, esta restricción también puede representarse extensionalmente mediante el conjunto de tuplas permitidas:
$$\{(1,1,1,1), (1,1,1,2), (1,1,2,1), (1,1,2,2), (2,1,2,2), (1,2,2,2),$$
$$(1,2,1,2), (1,2,2,1),(2,1,1,2), (2,1,2,1), (2,2,2,2)\}$$
o mediante el conjunto de tuplas no permitidas:
$$\{(1,2,1,1), (2,1,1,1), (2,2,1,1), (2,2,1,2), (2,2,2,1)\}$$
!!!Tip:Ejemplo
Vamos a dar como ejemplo diversas representaciones de un mismo problema usando la representación CSP. Trabajaremos sobre el **problema de las N reinas**, que consiste en disponer en un tablero de ajedrez de tamaño $N\times N$, $N$ reinas de forma que no haya amenazas entre ningún par de ellas (recordemos que una reina amenaza a toda la fila, columna y diagonales de la casilla en la que se sitúa).

Observa las diferencias que se producen en la complejidad de las representaciones, tanto por el espacio de combinaciones en las soluciones como por las restricciones.
**Primera Representación:**
1. $X=\{R_1,\dots,R_N\}=\{R_i :\ 1 \leq i \leq N\}$
2. $D=\{(x,y):\ 1\leq x,y \leq N\}$, donde $R_i=(x_i,y_i)$
3. Las restricciones:
- No hay amenaza horizontal: $x_i \neq x_j$, para todo $i\neq j$.
- No hay amenaza vertical: $y_i \neq y_j$, para todo $i\neq j$.
- No hay amenaza en la diagonal principal: $x_i - x_j \neq y_i - y_j$, para todo $i \neq j$.
- No hay amenaza en la diagonal secundaria: $x_i - x_j \neq y_j - y_i$, para todo $i \neq j$.
(Las dos diagonales se pueden tratar conjuntamente con: $|x_i - x_j| \neq |y_i - y_j|$, para todo $i \neq j$)
En esta representación el dominio es finito y hace uso de restricciones binarias de obligación. Para $N=8$ hay $64^8$ posibles asignaciones y $126$ restricciones.
**Segunda Representación:**
1. $X=\{R_{i,j}:\ 1\leq x,y \leq N\}$ (una por cada casilla).
2. $D=\{0,1\}$
3. Las restricciones:
- $\displaystyle{\sum_i R_{i,j} \leq 1}$, para todo $1\leq j\leq N$.
- $\displaystyle{\sum_j R_{i,j} \leq 1}$, para todo $1\leq i\leq N$.
- $\displaystyle{\sum_{(i,j)\in D} R_{i,j} \leq 1}$, para toda $D$ diagonal.
En esta representación el dominio es finito y hace uso de restricciones de varias aridades. Para $N=8$ hay $64^2$ posibles asignaciones y unas $300$ restricciones.
**Tercera Representación:**
Similar a la anterior, pero por medio de predicados lógicos:
1. $X=\{R_{i,j}:\ 1\leq x,y \leq N\}$ (una por cada casilla).
2. $D=\{0,1\}$
3. Las restricciones:
- $(R_{i,j} \rightarrow \neg R_{i,j'})$, para todo $j' \neq j$.
- $(R_{i,j} \rightarrow \neg R_{i',j})$, para todo $i' \neq i$.
- $(R_{i,j} \rightarrow \neg R_{i+k,j+k})$, para todo $1\leq i+k, j+k \leq N$.
- $(R_{i,j} \rightarrow \neg R_{i+k,j-k})$, para todo $1\leq i+k, j-k \leq N$.
**Cuarta Representación:**
Haciendo uso de conocimiento implícito del problema (que va a haber una, y solo una, reina en cada columna):
1. $X=\{R_i :\ 1\leq i \leq N\}$
2. $D=\{1,\dots,N\}$
3. Las restricciones:
- $R_i \neq R_j$, para todo $i\neq j$.
- $|R_i - R_j| \neq |i - j|$, para todo $i\neq j$.
En esta representación el dominio es finito y hace uso de restricciones binarias. Para $N=8$ hay $8^8$ posibles asignaciones y unas $80$ restricciones.
# Problemas de Optimización de Restricciones (COP)
Los problemas de la vida real suelen incluir tanto restricciones **duras** como **blandas**. Por ejemplo, en los problemas de asignación de horarios, mientras que una restricción de recursos como *un profesor sólo puede dar una clase a la vez* debe satisfacerse, la petición de un profesor de tener su *horario concentrado en sólo dos días* es sólo una preferencia, no es esencial.
Cuando formalizamos problemas que tienen restricciones duras y blandas, obtenemos una red de restricciones aumentada con una **función de coste global** (también llamada **función de criterio** o **función objetivo**) sobre todas las variables. Los **problemas de optimización de restricciones** (**COP**) encuentran una asignación completa de valores a todas las variables, satisfaciendo las restricciones duras y optimizando la función de coste global.
Numerosos problemas industriales pueden modelarse como tareas de optimización de restricciones. En particular, las tareas de programación y diseño implican restricciones duras y blandas.
!!!Tip:Ejemplo
Consideremos el caso del mantenimiento de las unidades de generación de energía. Una central eléctrica típica consta de una o dos docenas de unidades de generación de energía que pueden programarse individualmente para su mantenimiento preventivo. Se conoce de antemano tanto el tiempo necesario para el mantenimiento de cada unidad como una estimación razonablemente precisa de la demanda de energía de la central. El objetivo general de la programación del mantenimiento es determinar la duración y la secuencia de las paradas de las unidades individuales de generación de energía en un periodo de tiempo determinado, minimizando los costes de explotación y mantenimiento durante el periodo de planificación en cuestión, sujeto a diversas restricciones. La programación está influida por muchos factores, como la duración del periodo de mantenimiento de cada unidad, las restricciones sobre el momento en que se puede realizar el mantenimiento, la demanda de energía prevista para toda la planta y el coste variable del mantenimiento y del combustible en diferentes momentos del periodo de planificación.
!!!Tip:Ejemplo
Otro ejemplo que podemos aportar es el problema de la subasta combinatoria, donde los licitadores pueden hacer una oferta por varios artículos. Esto plantea al subastador el problema de determinar la selección óptima de ofertas para maximizar los ingresos. Más formalmente, dado un conjunto de artículos $S = \{a_1,\dots ,a_n\}$ y un conjunto de pujas $B = \{b_1,\dots, b_m\}$, donde cada puja es $b_i = (S_i, r_i)$, con $Si\subseteq S$ un conjunto de artículos y $r_i$ es el coste a pagar por la puja $b_i$. La tarea consiste en encontrar un subconjunto de pujas $B'\subseteq B$ tal que dos pujas cualesquiera de $B'$ no compartan un artículo y se maximice $C(B')=\displaystyle{\sum_{b_i\in B'}} r_i$.
Una importante fuente de problemas de optimización se encuentra en el área de la planificación en IA. En el marco determinista, la tarea consiste en encontrar una secuencia corta de acciones (un plan) que logre un conjunto de objetivos a partir de un estado inicial dado. Los problemas de planificación pueden formularse como tareas de satisfacción de restricciones asumiendo un plan de longitud fija. La planificación puede formularse alternativamente como tareas de optimización de restricciones, cuando la función de coste global que debe optimizarse es el número de acciones (o más generalmente, el coste) del plan.
En última instancia, cada tarea de satisfacción de restricciones puede verse como un problema de optimización de restricciones. Cuando no se pueden satisfacer todas las restricciones, es posible que se quiera encontrar una solución que maximice el número de restricciones satisfechas. Este problema se conoce como problema **Max-CSP**, y la versión para **SAT** se llama **Max-SAT**. A las restricciones también se les puede asignar pesos de importancia, en cuyo caso la tarea es minimizar la suma ponderada de las restricciones violadas.
Los problemas de optimización combinatoria se han investigado ampliamente en la comunidad de Investigación Operativa en las últimas décadas. Más recientemente, dentro de la comunidad de procesamiento de restricciones ha surgido un nuevo enfoque para formular, modelar, aprender y resolver las restricciones blandas.
Los principales enfoques para resolver tareas de optimización de restricciones discretas que amplían los métodos de satisfacción de restricciones. En concreto, los métodos de optimización de restricciones pueden dividirse en esquemas **basados en búsqueda** y esquemas **basados en inferencia**. El algoritmo de búsqueda más común para la optimización de restricciones es el **branch-and-bound**, mientras que el algoritmo de inferencia más célebre es el de **programación dinámica**.
!!!Def
Un problema de optimización de restricciones es un problema de satisfacción restricciones como hemos visto en los apartados enteriores aumentado con una función de costes. En las condiciones de un CSP, si añadimos a la terna $(X,D,C)$ una cuarta componente para calcular costes de restricciones que, a cada restricción y tupla de valores de variables sobre que se evalúa, le asigna un peso real positivo, entonces la tarea de *Optimización de Restricciones* consistirá en encontrar la tupla de valores que hace que el coste total de las restricciones sea óptima (máxima o mínima, dependiendo de las necesidades del problema).
!!!Tip:Ejemplo
Consideremos el problema de la subasta combinatoria anterior. Un enfoque sencillo para modelar este problema como un COP es asociar cada oferta $b_i$ con una variable que tiene dos valores $\{0,1\}$, donde $b_i=1$ si la oferta es seleccionada por el subastador, y $0$ en caso contrario. Para cada dos pujas que comparten un elemento existe una restricción binaria que prohíbe la asignación de $1$ a ambas variables de puja. Por tanto, las variables son $b_1,\dots, b_r$ con dominios $\{0,1\}$, y las restricciones: si $b_i$ y $b_j$ comparten un artículo, existe una restricción $R_{ij}$ que dice $\neg (b_i = 1 \wedge b_j = 1)$.
Consideremos una instancia de problema dada por las siguientes ofertas: $b_1 = \{ 1, 2, 3, 4\}$, $b_2 = \{2, 3, 6\}$, $b_3 = \{1, 5, 4\}$, $b_4 = \{2, 8\}$, $b_5 = \{5, 6\}$, y los costes $r_1 = 8$, $r_2 = 6$, $r_3 = 5$, $r_4 = 2$, $r_5 = 2$. En este caso las restricciones existentes serían $R_{12}$, $R_{13}$, $R_{14}$, $R_{24}$, $R_{25}$, $R_{35}$. Se puede comprobar que la solución óptima viene dada por $b_1 =0$, $b_2 = 1$, $b_3 = 1$, $b_4 = 0$, $b_5 = 0$. Es decir, la selección de las ofertas $b_2$ y $b_3$ es una elección óptima con un coste total de $11$.
!!!
Siempre podemos encontrar una solución a un COP resolviendo una serie de CSPs, donde en cada etapa se añade una restricción adicional que dice que el coste total sea mayor que una cierta constante $c_i$, donde $c_1\geq c_2\geq \dots$. Es decir, el límite de coste se incrementa gradualmente, encontrándose una nueva solución cada vez. Finalmente, el límite de coste es tan alto que no existe ninguna solución, y la última solución encontrada es óptima. Incluso con esta solución tan ingenua podemos imaginar un algoritmo de control más sofisticado basado, por ejemplo, en un enfoque de búsqueda binaria.
Esta reducción del problema de optimización al problema de satisfacción permite claramente aplicar a la optimización todas las técnicas de tratamiento que se desarrollen para la satisfacción de restricciones. Sin embargo, la resolución de múltiples problemas CSP puede evitarse utilizando un enfoque más directo según los paradigmas de búsqueda, inferencia y sus híbridos.
En lo que sigue nos centraremos en las aproximaciones a CSP, ya que es la parte común a ambos problemas.
# Consistencia en un CSP
Al igual que ocurre con los algoritmos de búsqueda generales, una forma común de crear algoritmos de búsqueda sistemática para la resolución de CSP tienen como base la búsqueda basada en **backtracking**. Sin embargo, esta búsqueda sufre con frecuencia una explosión combinatoria en el espacio de búsqueda, y por lo tanto no es por sí solo un método suficientemente eficiente para resolver este tipo de problemas.
Una de las principales dificultades con las que nos encontramos en los algoritmos de búsqueda es la aparición de inconsistencias locales que van apareciendo continuamente. Las inconsistencias locales son valores individuales, o una combinación de valores de las variables, que no pueden participar en la solución porque no satisfacen alguna propiedad de consistencia.
En la literatura se han propuesto varias técnicas de consistencia local como formas de mejorar la eficiencia de los algoritmos de búsqueda. Estas técnicas borran valores inconsistentes de las variables o inducen restricciones implícitas que ayudan a podar el espacio de búsqueda.
## Consistencia de Nodo ($1$-consistencia)
La consistencia local más simple de todas es la **consistencia de nodo** o **nodo-consistencia**. Forzar este nivel de consistencia nos asegura que todos los valores en el dominio de una variable satisfacen todas las restricciones unarias sobre esa variable.
**Definición.** Un problema es **nodo-consistente** si y sólo si todas sus variables son nodo-consistentes:
$$\forall x_i \in X,\ \forall C_i,\ \exists a \in D_i \ :\ a\ satisface\ C_i$$
## Consistencia de Arco ($2$-consistencia)
**Definición.** Un problema binario es **arco-consistente** si para cualquier par de variables $x_i$ y $x_j$, para cada valor $a$ en $D_i$ hay al menos un valor $b$ en $D_j$ tal que las asignaciones $(x_i ,a)$ y $(x_j ,b)$ satisfacen la restricción entre $x_i$ y $x_j$.
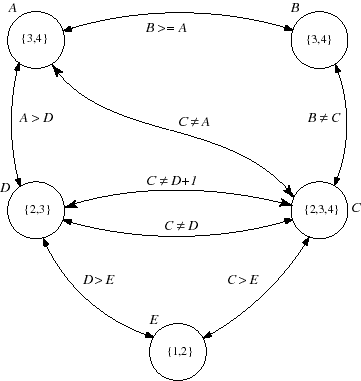
Cualquier valor en el dominio $D_i$ de la variable $x_i$ que no es arco-consistente puede ser eliminado de $D_i$ ya que no puede formar parte de ninguna solución. El dominio de una variable es arco-consistente si todos sus valores son arco-consistentes.
!!!Tip:Ejemplo
La restricción $C_{ij} = x_i < x_j$, donde $x_i\in [3,6]$ y $x_j\in [8,10]$ es consistente, ya que para cada valor $a \in [3,6]$ hay al menos un valor $b \in [8,10]$ de manera que se satisface la restricción $C_{ij}$. Sin embargo, si la restricción fuese $C_{ij} = x_i > x_j$ no sería arco-consistente.
!!!
Un **problema es arco-consistente** si y sólo si todos sus arcos son arco-consistentes:
$$\forall\ C_{ij} \in C,\ \forall a \in D_i,\ \exists b \in D_j \ : \ b \mbox{ es un soporte para } a \mbox{ en } C_{ij}$$
## Consistencia de caminos ($3$-consistencia)
La consistencia de caminos es un nivel más alto de consistencia local que la arco-consistencia. La consistencia de caminos requiere, para cada par de valores $a$ y $b$ de dos variables $x_i$ y $x_j$, que la asignación de $((x_i,a), (x_j,b))$ satisfaga la restricción entre $x_i$ y $x_j$, y que además exista un valor para cada variable a lo largo del camino entre $x_i$ y $x_j$ de forma que todas las restricciones a lo largo del camino se satisfagan.
Un problema satisface la consistencia de caminos si y sólo si todo par de variables $(x_i ,x_j)$ verifica la consistencia de caminos. Cuando un problema satisface la consistencia de caminos y además es nodo-consistente y arco-consistente se dice que **satisface fuertemente la consistencia de caminos**.
## Consistencia Global
A veces es deseable una noción más fuerte que la consistencia local.
!!!Def
**Definición.** Dado un CSP $(X,D,C)$, se dice que es **globalmente consistente** si y sólo si para cada variable $x_i$ y cada valor posible para ella, $a \in D_i$, la asignación $(x_i, a)$ forma parte de una solución del CSP.
# El Árbol de Búsqueda
Las posibles combinaciones de la asignación de valores a las variables en un CSP genera un espacio de búsqueda al que se puede dotar de una estructura específica para ser visto como un **árbol de búsqueda**. De esta forma, después podremos recorrerlo siguiendo la estrategia que queramos. La búsqueda mediante **backtracking**, que es la base sobre la que se soportan la mayoría de algoritmos para CSP, corresponde a la tradicional exploración en [profundidad DFS](http://www.cs.us.es/~fsancho/?e=95) en el árbol de búsqueda.
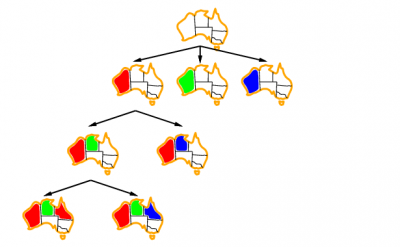
La forma más habitual de darle estructura de árbol pasa por asumir que el orden de las variables es estático y no cambia durante la búsqueda, y entonces un nodo en el nivel $k$ del árbol de búsqueda representará un estado donde las variables $x_1 ,...,x_k$ están asignadas a valores concretos de sus dominios mientras que el resto de variables, $x_{k+1} ,...,x_n$, no lo están. Podemos asignar cada nodo en el árbol de búsqueda con la tupla formada por las asignaciones llevadas a cabo hasta ese momento, donde la raíz del árbol de búsqueda representa la tupla vacía, en la que ninguna variable tiene asignado valor alguno.
Los nodos en el primer nivel son $1$−tuplas que representan estados donde se les ha asignado un valor a la variable $x_1$. Los nodos en el segundo nivel son $2$−tuplas que representan estados donde se le asignan valores a las variables $x_1$ y $x_2$, y así sucesivamente. Un nodo del nivel $k$ es hijo de un nodo del nivel $k-1$ si la tupla asociada al hijo es una extensión de la de su padre añadiendo una asignación para la variable $x_k$. Si $n$ es el número de variables del problema, los nodos en el nivel $n$, que representan las hojas del árbol de búsqueda, son $n$−tuplas, que representan la asignación de valores para todas las variables del problema. De esta manera, si una $n$−tupla es consistente, entonces es solución del problema. Un nodo del árbol de búsqueda es consistente si la asignación parcial actual es consistente, o en otras palabras, si la tupla correspondiente a ese nodo es consistente.
# Backtracking Cronológico
El algoritmo de búsqueda sistemática más conocido para resolver CSP se denomina **Algoritmo de Backtracking Cronológico** (**BT**). Si asumimos un orden estático de las variables y de los valores en las variables, este algoritmo funciona de la siguiente manera:
1. Selecciona la siguiente variable de acuerdo al orden de las variables y le asigna su próximo valor.
2. Esta asignación de la variable se comprueba en todas las restricciones en las intervienen la variable actual y las anteriores:
- Si todas las restricciones se han satisfecho, vuelve al punto 1.
- Si alguna restricción no se satisface, entonces la asignación actual se deshace y se prueba con el próximo valor de la variable actual.
3. Si no se encuentra ningún valor consistente entonces tenemos una situación sin salida y el algoritmo retrocede a la variable anteriormente asignada y prueba asignándole un nuevo valor.
4. Si asumimos que estamos buscando una sola solución, BT finaliza cuando a todas las variables se les ha asignado un valor, en cuyo caso devuelve una solución, o cuando todas las combinaciones de variable-valor se han probado sin éxito, en cuyo caso no existe solución.
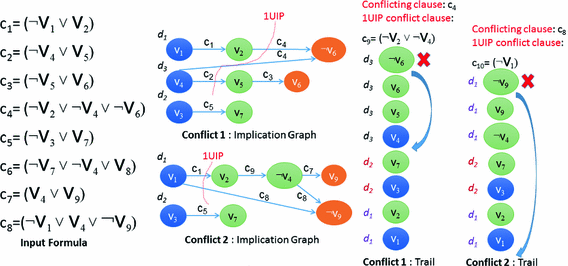
Es fácil generalizar BT a restricciones no binarias. Cuando se prueba un valor de la variable actual, el algoritmo comprobará todas las restricciones en las que sólo intervienen la variable actual y las anteriores. Si una restricción involucra a la variable actual y al menos una variable futura, entonces esta restricción no se comprobará hasta que se hayan asignado todas las variables futuras de la restricción.
BT es un algoritmo muy simple pero muy ineficiente. El problema es que tiene una visión local del problema. Sólo comprueba restricciones que están formadas por la variable actual y las pasadas, e ignora la relación entre la variable actual y las futuras. Además, este algoritmo es ingenuo en el sentido de que no *recuerda* las acciones previas, y como resultado, puede repetir la misma acción varias veces innecesariamente. Para ayudar a combatir este problema, se han desarrollado algunos algoritmos de búsqueda más robustos. Estos algoritmos se pueden dividir en algoritmos **look-back** y algoritmos **look-ahead**.
## Algoritmos Look-Back
Los **algoritmos look-back** tratan de explotar la información del problema para comportarse más eficientemente en las situaciones sin salida. Al igual que el backtracking cronológico, los algoritmos look-back llevan a cabo la comprobación de la **consistencia hacia atrás**, es decir, entre la variable actual y las pasadas.
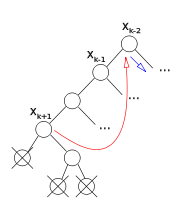
**Backjumping (BJ)** es parecido a BT excepto que se comporta de una manera más inteligente cuando encuentra situaciones sin salida. En vez de retroceder a la variable anteriormente instanciada, BJ salta a la variable más profunda (más cerca de la variable actual) $x_j$ que está en conflicto con la variable actual $x_i$ donde $j < i$ (una variable instanciada $x_j$ está en conflicto con una variable $x_i$ si la instanciación de $x_j$ evita uno de los valores en $x_i$, debido a la restricción entre ellas). Cambiar la instanciación de $x_j$ puede hacer posible encontrar una instanciación consistente para la variable actual.
Una variante, **conflict-directed Backjumping (CBJ)** tiene un comportamiento de salto hacia atrás más sofisticado que BJ, donde se almacena para cada variable un conjunto de conflictos mutuos que permite no repetir conflictos existentes a la vez que saltar a variables anteriores como hace BJ.
## Algoritmos look-Ahead
Los algoritmos look-back tratan de reforzar el comportamiento de BT mediante un comportamiento más inteligente cuando se encuentran en situaciones sin salida. Sin embargo, todos ellos llevan a cabo la comprobación de la consistencia solamente hacia atrás, ignorando las futuras variables. Los **algoritmos Look-Ahead** hacen una comprobación hacia adelante en cada etapa de la búsqueda, es decir, llevan a cabo las comprobaciones para obtener las inconsistencias de las variables futuras involucradas además de las variables actual y pasadas. De esa manera, las situaciones sin salida se pueden identificar antes y los valores inconsistentes se pueden descubrir y podar para las variables futuras.
**Forward checking (FC)** es uno de los algoritmos look-ahead más famoso. En cada etapa de la búsqueda, FC comprueba hacia adelante la asignación actual con todos los valores de las futuras variables que están restringidas con la variable actual. Los valores de las futuras variables que son inconsistentes con la asignación actual son temporalmente eliminados de sus dominios (solo para la rama actual de búsqueda). Si el dominio de una variable futura se queda vacío, la instanciación de la variable actual se deshace y se prueba con un nuevo valor. Si ningún valor es consistente, entonces se lleva a cabo BT estándar. FC garantiza que, en cada etapa, la solución parcial actual es consistente con cada valor de cada variable futura. Además cuando se asigna un valor a una variable, solamente se comprueba hacia adelante con las futuras variables con las que está involucrada. Así mediante la comprobación hacia adelante, FC puede identificar antes las situaciones sin salida y podar el espacio de búsqueda. Se puede ver como aplicar un simple paso de arco-consistencia sobre cada restricción que involucra la variable actual con una variable futura después de cada asignación de variable.
El proceso que sigue Forward Checking podría resumirse en el siguiente:
1. Seleccionar $x_i$.
2. Instanciar $(x_i , a_i) : a_i \in D_i$.
3. Razonar hacia adelante (check-forward): Eliminar de los dominios de las variables aún no instanciadas con un valor aquellos valores inconsistentes con respecto a la instanciación $(x_i, a_i)$, de acuerdo al conjunto de restricciones.
4. Si quedan valores posibles en los dominios de todas las variables por instanciar, entonces:
- Si $i < n$, incrementar $i$, e ir al paso 1.
- Si $i = n$, parar devolviendo la solución.
5. Si existe una variable por instanciar sin valores posibles en su dominio entonces retractar los efectos de la asignación $(x_i, a_i)$:
- Si quedan valores por intentar en $D_i$, ir al paso 2.
- Si no quedan valores:
- Si $i > 1$, decrementar $i$ y volver al paso 2.
- Si $i = 1$, salir sin solución.
Forward checking se ha combinado con algoritmos look-back para generar algoritmos híbridos. Por ejemplo, **forward checking con conflict-directed backjumping (FC-CBJ)** es un algoritmo híbrido que combina el movimiento hacia adelante de FC con el movimiento hacia atrás de CBJ, y de esa manera tiene las ventajas de ambos algoritmos.
# Heurísticas
Los algoritmos de búsqueda para CSP vistos hasta el momento hacen uso explícito del orden en el cual se van a seleccionar las variables, así como el orden en el que se van a instanciar sus valores. Seleccionar el orden correcto de las variables y de los valores puede mejorar notablemente la eficiencia de resolución. De igual forma, puede resultar importante una ordenación adecuada de las restricciones del problema.
Veamos algunas de las más importantes heurísticas de ordenación de variables y de ordenación de valores.
## Ordenación de Variables
Muchos resultados experimentales han mostrado que el orden en el cual las variables son asignadas durante la búsqueda puede tener una impacto significativo en el tamaño del espacio de búsqueda explorado. Generalmente, las heurísticas de ordenación de variables tratan de seleccionar lo antes posible las variables que más restringen a las demás. La intuición indica que es mejor tratar de asignar lo antes posible las variables más restringidas y de esa manera identificar las situaciones sin salida lo antes posible y así reducir el número de vueltas atrás.
La ordenación de variables puede ser estática o dinámica. Las heurísticas de ordenación de variables estáticas generan un orden fijo de las variables antes de iniciar la búsqueda, basado en información global derivada del grafo de restricciones inicial. Las heurísticas de ordenación de variables dinámicas pueden cambiar el orden de las variables dinámicamente basándose en información local que se genera durante la búsqueda.
**Heurísticas de ordenación de variables estáticas**
Se han propuesto varias heurísticas de ordenación de variables estáticas. Estas heurísticas se basan en la información global que se deriva de la topología del grafo de restricciones original que representa el CSP:
1. **Minimum Width (MW)**: La anchura de la variable $x$ es el número de variables que están antes de $x$, de acuerdo a un orden dado, y que son adyacentes a $x$ (en el grafo de restricciones). La anchura de un orden es la máxima anchura de todas las variables bajo ese orden. La anchura de un grafo de restricciones es la anchura mínima de todos los posibles ordenes. Después de calcular la anchura de un grafo de restricciones, las variables se ordenan desde la última hasta la primera en anchura decreciente. Esto significa que las variables que están al principio de la ordenación son las más restringidas y las variables que están al final de la ordenación son las menos restringidas. Asignando las variables más restringidas al principio, las situaciones sin salida se pueden identificar antes y además se reduce el número de vueltas atrás.
2. **Maximun Degree (MD)**: ordena las variables en un orden decreciente de su grado en el grafo de restricciones. El grado de un nodo se define como el número de nodos que son adyacentes a él. Esta heurística también tiene como objetivo encontrar un orden de anchura mínima, aunque no lo garantiza.
3. **Maximun Cardinality (MC)**: selecciona la primera variable arbitrariamente y después en cada paso, selecciona la variable que es adyacente al conjunto más grande de las variables ya seleccionadas.
**Heurísticas de ordenación de variables dinámicas**
El problema de los algoritmos de ordenación estáticos es que no tienen en cuenta los cambios en los dominios de las variables causados por la propagación de las restricciones durante la búsqueda, o por la densidad de las restricciones. Esto se debe a que estas heurísticas generalmente se utilizan en algoritmos de comprobación hacia atrás donde no se lleva a cabo la propagación de restricciones.
Se han propuesto varias heurísticas de ordenación de variables dinámicas que abordan este problema. La más común se basa en el **principio del primer fallo** (**FF**) que sugiere que para tener éxito deberíamos intentar primero donde sea más probable que falle. De esta manera las situaciones sin salida pueden identificarse antes y además se ahorra espacio de búsqueda. De acuerdo con el principio de FF, en cada paso seleccionaríamos la variable más restringida.
La heurística FF también conocida como **heurística Minimum Remaining Values (MRV)**, trata de hacer lo mismo seleccionando la variable con el dominio más pequeño. Se basa en la intuición de que si una variable tiene pocos valores, entonces es más difícil encontrar un valor consistente. Cuando se utiliza MRV junto con algoritmos look-back, equivale a una heurística estática que ordena las variables de forma ascendente con el tamaño del dominio antes de llevar a cabo la búsqueda. Cuando MRV se utiliza en conjunción con algoritmos look-ahead, la ordenación se vuelve dinámica, ya que los valores de las futuras variables se pueden podar después de cada asignación de variables. En cada etapa de la búsqueda, la próxima variable a asignar es la variable con el dominio más pequeño.
Algunos resultados experimentales prueban que todas las heurísticas de ordenación de variables estáticas son peores que el algoritmo MRV.
## Ordenación de Valores
Se ha realizado poco trabajo sobre heurísticas para la ordenación de valores. La idea básica que hay detrás de las heurísticas de ordenación de valores es seleccionar el valor de la variable actual que más probabilidad tenga de llevarnos a una solución. La mayoría de las heurísticas propuestas tratan de seleccionar el valor menos restrictivo de la variable actual, es decir, el valor que menos reduce el número de valores útiles para las futuras variables.
Una de las heurísticas de ordenación de valores más conocida es la **heurística de mínimo-conflicto**. Básicamente, esta heurística ordena los valores de acuerdo a los conflictos en los que éstos están involucrados con las variables no instanciadas. Esta heurística asocia a cada valor $a$ de la variable actual, el número total de valores en los dominios de las futuras variables adyacentes que son incompatibles con $a$. El valor seleccionado es el asociado a la suma más baja. Esta heurística se puede generalizar para CSP no binarios de forma directa.
## Otras técnicas de resolución de CSP: Métodos estocásticos
Además de las técnicas sistemáticas y completas, existen también aproximaciones no sistemáticas e incompletas incluyendo heurísticas (tales como hill climbing, búsqueda tabú, enfriamiento simulado, algoritmos genéticos o algoritmos de hormigas).
Estas técnicas pueden considerarse como adaptativas en el sentido de que comienzan su búsqueda en un punto aleatorio del espacio de búsqueda y lo modifican repetidamente utilizando heurísticas hasta que alcanza la solución (con un cierto número de iteraciones), y ya las hemos revisado, en otros contextos, en entradas anteriores. Estos métodos son generalmente robustos y buenos para encontrar un mínimo global en espacios de búsqueda grandes y complejos, aunque no aseguran que se pueda encontrar debido a la aleatoriedad del punto de inicio. Por ello, es común repetir varias veces la aplicación de estos algoritmos cambiando al azar el punto de partida.
# Aplicaciones
CSP se ha aplicado con mucho éxito a muchos problemas de áreas tan diversas como planificación, scheduling, generación de horarios, empaquetamiento, diseño y configuración, diagnosis, modelado, recuperación de información, CAD/CAM, criptografía, etc.
Los problemas de asignación fueron quizás el primer tipo de aplicación industrial que fue resuelta con herramientas de restricciones. Entre los ejemplos típicos iniciales figuran la asignación de rampas en los aeropuertos, donde los aviones deben aparcar en una rampa disponible durante la estancia en el aeropuerto, o la asignación de pasillos de salida y atracaderos.
Otra área de aplicación de restricciones típica es la asignación de personal donde las reglas de trabajo y las regulaciones laborales imponen una serie de restricciones difíciles de satisfacer. El principal objetivo en este tipo de problemas es balancear el trabajo entre las personas contratadas de manera que todos tengan las mismas ventajas. Existen sistemas desarrollados para la generación de turnos de enfermeras en los hospitales, para la asignación de tripulación a los vuelos, la asignación de plantillas en compañías ferroviarias o para la obtención de redes ferroviarias óptimas.
Sin embargo, una de las áreas de aplicación más exitosa de los CSP con dominios finitos es en los problemas de secuenciación o scheduling donde, de nuevo, las restricciones expresan las limitaciones existentes en la vida real. El CSP se utiliza para la secuenciación de actividades industriales, forestales, militares, etc. En general, su uso se está incrementando debido a las tendencias de las empresas de trabajar bajo demanda.
# Tendencias
Las tendencias actuales en CSP pasan por desarrollar técnicas para resolver determinados problemas de satisfacción de restricciones basándose principalmente en la topología de las redes de restricciones. Entre estas tendencias podemos destacar las siguientes:
1. Técnicas para resolver problemas con muchas restricciones.
2. Técnicas para resolver problemas con muchas variables y restricciones, donde puede resultar conveniente la paralelización o distribución del problema de forma que éste se pueda dividir en un conjunto de subproblemas más fáciles de manejar.
3. Técnicas combinadas de satisfacción de restricciones con métodos de investigación operativa con el fin de obtener las ventajas de ambas propuestas.
4. Técnicas de computación evolutiva, donde los [algoritmos genéticos](http://www.cs.us.es/~fsancho/?e=65) al igual que las [redes neuronales](http://www.cs.us.es/~fsancho/?e=72), se han ido ganando poco a poco el reconocimiento de los investigadores como técnicas efectivas en problemas de gran complejidad. Se distinguen por utilizar estrategias distintas a la mayor parte de las técnicas de búsqueda clásicas y por usar operadores probabilísticos más robustos que los operadores determinísticos.
5. Otros temas de interés son heurísticas inspiradas biológicamente, tales como [colonias de hormigas](http://www.cs.us.es/~fsancho/?e=71), [optimización por enjambres de partículas](http://www.cs.us.es/~fsancho/?e=70), algoritmos meméticos, algoritmos culturales, búsqueda dispersa, etc.