**SVRAI**
Optimización de Restricciones Distribuida (DisCOP)
Definiciones y Algoritmos
> Un contenido más detallado del tema que se trata en este capítulo se puede encontrar en la Tesis Doctoral
> [A Class of Algorithms for Distributed Constraint Optimization](http://www.ppgia.pucpr.br/~fabricio/ftp/Aulas/Mestrado/AS/Artigos-Apresentacoes/DCOP/DPOP-Petcu2007thesis.pdf),
> de Adrian Petcu.
Como hemos visto en el [tema anterior](DisCSP.md.html), la **Satisfacción de Restricciones Distribuida** (**DisCSP**) es un elegante formalismo desarrollado para abordar problemas de satisfacción de restricciones bajo varios supuestos de modelos distribuidos ([#Collin1], [#Solotorevsky], [#Sycara], [#Yokoo1]). Cuando las soluciones tienen grados de calidad, o coste, el problema se convierte en un problema de optimización y se puede formular como un **Problema de Optimización de Restricciones** o **COP** ([#Schiex]). En los últimos años ha aumentado la investigación centrada en el marco más general del **COP distribuido**, o **DisCOP** ([#Gershman], [#Modi], [#Petcu], [#Zhang]).
Informalmente, tanto en el marco DisCSP como en el DisCOP, el problema se expresa como un conjunto de subproblemas individuales, cada uno de los cuales pertenece a un agente diferente. El subproblema de cada agente está conectado con algunos de los subproblemas de los agentes vecinos a través de restricciones sobre variables compartidas. Como en el caso centralizado, el objetivo es encontrar una solución globalmente óptima. Pero ahora, el modelo de cálculo está restringido. El problema se distribuye entre los agentes, que sólo pueden liberar información mediante el intercambio de mensajes entre los agentes que comparten información relevante, según un algoritmo especificado.
Los CSP y COP centralizados son un área de investigación madura, con muchas técnicas bastante eficientes desarrolladas en las últimas tres décadas. En comparación con las versiones centralizadas, los problemas distribuidos están todavía en sus inicios, y por ello la mayoría de los algoritmos actuales suelen tratar de adaptar y ampliar sus homólogos centralizados a entornos distribuidos.
!!!
Sin embargo, es muy importante tener en cuenta que las medidas de rendimiento de los algoritmos distribuidos son radicalmente diferentes de las que se aplican a los centralizados. En concreto, si en la optimización centralizada el tiempo de cálculo es el principal cuello de botella, **en la optimización distribuida es más bien la comunicación el factor limitante**. De hecho, en la mayoría de los escenarios, **el paso de mensajes es órdenes de magnitud más lento que el cálculo local**. Por lo tanto, resulta evidente que es deseable diseñar algoritmos que requieran una cantidad mínima de comunicación para encontrar la solución óptima. Esta importante diferencia hace que el diseño de algoritmos eficientes de optimización distribuida sea una tarea no trivial, y no se puede esperar simplemente que una simple adaptación distribuida de un algoritmo centralizado exitoso funcione con la misma eficiencia.
# Definiciones y notación
Comenzamos esta sección introduciendo el Problema de Optimización de Restricciones (COP) centralizado ([#Bertele], [#Schiex]). Formalmente,
!!!Def: Definición (COP)
Un **problema discreto de optimización de restricciones** (**COP**) es una tupla $(X,D,R)$ tal que:
- $X = \{X_1, \dots, X_n\}$ es un conjunto de variables.
- $D = \{d_1, \dots, d_n\}$ es un conjunto de dominios de variables discretas y finitas.
- $R = \{r_1, \dots, r_m\}$ es un conjunto de funciones de utilidad, donde cada $r_i : d_{i_1} \times \dots \times d_{i_k} \to \mathbb{R}$, que asigna una utilidad (recompensa) a cada combinación posible de valores de las variables. Las cantidades negativas significan costes.
El objetivo es encontrar una instanciación completa para las variables $X_i$ que maximice la suma de utilidades de las funciones de utilidad individuales. Formalmente,
$$X^* = \arg\max_X (\sum_{r_i\in R}ri(X))$$
donde los valores de $r_i$ son los valores correspondientes a la instanciación particular $X$. El grafo de restricciones es un grafo que tiene un nodo para cada variable $X_i \in X$ y una hiper-arista para cada relación $r_i\in R$.
Teniendo en cuenta que una **restricción dura** (que prohíbe ciertas combinaciones de valores) es un caso especial de función de utilidad (que asigna $0$ a las tuplas factibles, y $-\infty$ a las no factibles), podemos definir un Problema de Satisfacción de Restricciones como un caso especial de un COP:
!!!Def:Definición (CSP)
Un problema discreto de satisfacción de restricciones (CSP) es un COP $(X,D,R)$ tal que todas las relaciones $r_i\in R$ son restricciones duras.
!!!note:Observación (Resolución de CSPs)
Por tanto, los CSPs pueden ser resueltos con algoritmos diseñados para optimización: el algoritmo tiene que buscar la solución de máximo coste (que es $0$, si el problema es satisfacible).
!!!def:Definición (DisCOP)
Un **problema discreto de optimización de restricciones distribuidas** (**DisCOP**) es una tupla $(A,COP,R^{ia})$ tal que:
- $A = \{A_1, \dots , A_k\}$ es un conjunto de agentes.
- $COP = \{COP_1,\dots,COP_k\}$ es un conjunto de COPs disjuntos y centralizados; cada $COP_i$ se denomina **subproblema local del agente $A_i$**, que es propiedad y está controlado por el agente $A_i$.
- $R^{ia} = \{r_1, \dots, r_n\}$ es un conjunto de funciones de utilidad interagente definidas sobre variables de varios subproblemas/agentes locales diferentes $COP_i$. Cada $r_i$ expresa las recompensas obtenidas por los agentes involucrados en $r_i$ por alguna decisión conjunta. Los agentes implicados en $r_i$ tienen pleno conocimiento de $r_i$.
Informalmente, un DisCOP es una instancia multiagente de un COP en la que cada agente tiene su propio subproblema local. Sólo el agente propietario tiene pleno conocimiento y control de sus variables y restricciones locales. Los subproblemas locales, propiedad de diferentes agentes, pueden estar conectados por funciones de utilidad interagentes $R^{ia}$ que especifican la utilidad que los agentes implicados extraen de alguna decisión conjunta. Las restricciones duras interagentes que prohíben o imponen algunas combinaciones de decisiones pueden simularse como en un COP mediante funciones de utilidad que asignan $0$ a las tuplas factibles y $-\infty$ a las no factibles. Las restricciones duras entre agentes suelen utilizarse para modelar el conocimiento específico del dominio, como *un recurso puede asignarse sólo una vez* o *tenemos que acordar la hora de inicio de una reunión*.
Las variables de cada agente, $X_i$, se particionan en las llamadas **variables externas o de interfaz**, $X^{ext}_i \subseteq X_i$, que están conectadas mediante relaciones interagentes con variables de otros agentes, y las **variables internas**, $X^{int}_i \subseteq X_i$, que sólo son visibles para $A_i$.
Al igual que en el COP centralizado, definimos el **grafo de restricciones** como el grafo que se obtiene al conectar todas las variables que comparten alguna función de utilidad. Llamamos **vecinos** a dos agentes que comparten una función de utilidad interagente. El **grafo de interacción** es el que se obtiene conectando por parejas todos los agentes que son vecinos. Posteriormente, supondremos que sólo los agentes que están conectados en el grafo de interacción pueden comunicarse directamente.
Al igual que en el caso centralizado, la tarea consiste en encontrar la solución óptima al problema COP. Como hemos comentado, en el COP centralizado tradicional, tratamos de tener algoritmos que minimicen el tiempo de ejecución. En el DisCOP, la medida de rendimiento del algoritmo no es sólo el tiempo, sino también la carga de comunicación, normalmente el número de mensajes.
Como con los CSP centralizados, podemos utilizar la definición de un DisCOP para definir el DisCSP como un caso especial de un DCOP:
!!!def: Definición (DisCSP)
Un DisCSP es un DisCOP, $(A, COP, R^{ia})$ tal que:
* (a) Cada $COP_i\in COP$ es un CSP (todas las relaciones internas son restricciones duras), y
* (b) todos los $r_i\in R^{ia}$ son también restricciones duras.
!!!note: Observación (Resolución de DisCSPs)
Los DisCSPs se pueden resolver obviamente con algoritmos diseñados para DisCOP: el algoritmo tiene que buscar la solución de mínimo coste (que es $0$, si el problema es satisfacible).
!!!note: Observación
DCOP es **NP**-duro.
A continuación se presenta una lista de supuestos y convenciones que se utilizarán a lo largo del capítulo:
1. **Propiedad y control**: La definición anterior establece que cada agente $A_i$ posee y controla su propio subproblema local, $COP_i$. Para simplificar la exposición de los algoritmos, representamos todo el $COP_i$ (y el agente $A_i$ también) por una única meta-variable (normalmente, una tupla), $X_i$ , que toma como valores todo el conjunto de combinaciones de valores de las variables de interfaz de $A_i$. Por lo tanto, denotamos por *agente* bien a la entidad física propietaria del subproblema local, bien a la meta-variable correspondiente, y utilizamos *agente* y *variable* indistintamente.
2. **Patrones de identificación y comunicación**: Supondremos que cada agente tiene una identificación única y que conoce las identificaciones de sus vecinos. Además, supondremos que los agentes vecinos que comparten una restricción se conocen entre sí y pueden intercambiar mensajes. Sin embargo, los agentes que no están conectados por restricciones no pueden comunicarse directamente. Esta suposición es realista debido, por ejemplo, a la conectividad limitada en ciertos entornos, a la preocupación por la privacidad, a la sobrecarga de los canales de comunicación, a las políticas de seguridad, etc.
3. **Privacidad e interés propio**: Supondremos que los agentes no tienen intereses propios, es decir, que cada uno de ellos busca maximizar la suma global de la utilidad del sistema en su conjunto. Se espera que los agentes trabajen de forma cooperativa para encontrar la mejor solución al problema de optimización. Además, la privacidad no es una preocupación local, es decir, todas las restricciones y funciones de utilidad son conocidas por los agentes que participan en ellas. Esto no significa que un agente no implicado en una determinada restricción tenga que conocer su contenido, o incluso su existencia.
# Aplicaciones de Ejemplo
Hay una gran variedad de problemas de coordinación multiagente que pueden modelarse en el marco DisCOP. Algunos ejemplos son los problemas de horarios distribuidos ([#Kaplansky]), las constelaciones de satélites ([#Barrett]), la distribución de tareas en equipos ([#Tambe]), la programación descentralizada de talleres ([#Sycara]), las organizaciones humano-agente ([#Chalupsky]), las redes de sensores ([#Bejar]), etc.
A continuación daremos unas breves notas acerca de algunos de ellos:
### Programación de reuniones
Supongamos una gran organización con docenas de departamentos, repartidos en docenas de sitios, y que emplean a decenas de miles de personas. Los empleados de diferentes sedes/departamentos (son los agentes, $A$) tienen que programar cientos/miles de reuniones. Debido a las razones citadas anteriormente, no es deseable un enfoque centralizado para encontrar el mejor horario. La organización en su conjunto desea minimizar el coste de todo el proceso (alternativamente, maximizar la suma de las utilidades individuales de cada agente).
!!!def: Definición (Problema de programación de reuniones)
Un **problema de programación de reuniones** (**MSP**) es una tupla $(A,M,P, T , C, R)$ tal que:
- $A = \{A_1, \dots, A_k\}$ es un conjunto de agentes.
- $M = \{M_1, \dots, M_n\}$ es un conjunto de reuniones.
- $P = \{p_1, \dots, p_k\}$, donde cada $p_i \subseteq M$ representa el conjunto de reuniones a las que $A_i$ debe asistir.
- $T = \{t_1, \dots, t_n\}$ es un conjunto de franjas horarias donde pueden realizarse las reuniones.
- $C = \{c_1,\dots, c_m\}$ es un conjunto de restricciones (por ejemplo, ciertas reuniones no pueden solaparse).
- $R = \{r_1, \dots, rk\}$ es un conjunto de funciones de utilidad. Cada $r_i : p_i\times T \to \mathbb{R}$ representa la utilidad de $A_i$ para cada posible horario de sus reuniones.
Además, hay algunas restricciones duras: dos reuniones que comparten un participante no pueden solaparse, y los agentes que participan en una reunión deben acordar una franja horaria para la misma.
El objetivo de la optimización es encontrar el horario que sea factible (es decir, que respete todas las restricciones) y maximice la suma de las utilidades de los agentes.
!!!note:Proposición
MSP es **NP**-duro.
!!!Tip: Ejemplo 1 (Programación distribuida de reuniones)
Consideremos un ejemplo en el que 3 agentes, $\{A_1, A_2,A_3\}$, quieren encontrar la programación óptima para 3 reuniones. Donde $p_1 = \{M_1, M_3\}$, $p_2 = \{M_1, M_2, M_3\}$ y $p_3 = \{M_2, M_3\}$. Hay 3 franjas horarias posibles para organizar estas tres reuniones: $T=\{8AM, 9AM, 10AM\}$. Cada agente $A_i$ tiene un problema de programación local $COP_i$ compuesto por:
- variables $A_i\_M_j$ : una variable por cada reunión $M_j$ en la que el agente $A_i$ debe participar,
- dominios: las 3 franjas horarias posibles: 8AM, 9AM, 10AM,
- restricciones duras que imponen que no se superpongan dos de sus reuniones,
- funciones de utilidad: modelan las preferencias de los agentes.
Se añaden restricciones en función de los posibles solapamientos a evitar, por ejemplo, $c_{121}$ modela el hecho de que $A_1$ y $A_2$ deben ponerse de acuerdo sobre la franja horaria que se asignará a $M_1$.
Un modelo distribuido del problema de programación de reuniones permitiría que cada agente decidiera su propia programación de reuniones sin tener que recurrir a una autoridad central. Además, el modelo también preserva la autonomía de cada agente, en el sentido de que un agente puede elegir no establecer sus variables de acuerdo con el protocolo especificado. Suponiendo que este sea el caso, los demás agentes pueden decidir seguir su decisión, o celebrar la reunión sin él.
### Subastas combinatorias
Las subastas son una forma popular de asignar recursos o tareas a los agentes en un sistema multiagente. Esencialmente, los postores expresan ofertas para conseguir un bien. Normalmente, el mejor postor obtiene el bien por el precio ofrecido en su oferta (subastas de primer precio), pero también hay variantes en las que el bien se lo lleva la segunda oferta más alta (subastas de segundo precio o Vickrey).
Las subastas combinatorias (CA) son mucho más expresivas porque permiten a los licitadores expresar sus ofertas por paquetes de bienes, por lo que son más útiles cuando los bienes son complementarios o sustituibles (la valoración del paquete no es igual a la suma de las valoraciones de los bienes individuales).
Las CAs han recibido mucha atención desde hace unas décadas, y hay un gran número de trabajos que las tratan ([#Vries]). Además, su aplicación es más variada que la propia definición, y se pueden usar para otros problemas, como la asignación de recursos ([#Ostwald]), la asignación de tareas ([#Walsh]), etc.
Aunque hay muchos algoritmos disponibles para resolver este problema, la mayoría de ellos están centralizados, suponen la existencia de un subastador que recoge las ofertas y resuelve el problema con un método de optimización centralizado ([#Sandholm]), y hay pocos métodos no centralizados para resolverlos: [#Fujita] propone un algoritmo paralelo de tipo Branch and Bound, que funciona dividiendo el espacio de búsqueda entre múltiples agentes, pero solo por razones de eficiencia; en [#Narumanchi] se proponen varios algoritmos distribuidos, algunos subóptimos, y uno óptimo, pero que es computacionalmente caro (exponencial en el número de agentes).
!!!def: Definición (Subasta Combinatoria)
Una **subasta combinatoria** (**CA**) es una tupla $(A, G, B)$ tal que:
- $A = \{A_1, \dots, A_k\}$ es un conjunto de agentes ofertantes.
- $G = \{g_1, \dots, g_n\}$ es un conjunto de bienes (indivisibles).
- $B$ es un conjunto de ofertas. Una oferta $b^i_k$ expresada por un agente $A_i$ es una tupla $(G^i_k , v^i_k)$, donde $v^i_k$ es la valoración que el agente $A_i$ tiene para el conjunto de bienes $G^i_k\subseteq G$; cuando $A_i$ no obtiene todo el conjunto $G^i_k$ , entonces $v^i_k = 0$.
Una asignación factible es una aplicación, $S: B \to \{True,False\}$, que asigna un valor de verdad a cada oferta ($S(b^i_k)$ significa que $A_i$ gana la oferta $b^i_k$) tal que:
$$\forall\ b^i_k, b^m_l\ \in B\ (\exists\ g_j \in G\ (g_j \in G^i_k \wedge g_j \in G^m_l) \rightarrow \neg S(b^i_k) \vee \neg S(b^m_l))$$
En otras palabras, no hay dos ofertas que compartan un bien que puedan ganar al mismo tiempo (porque se supone que los bienes son indivisibles).
El valor de una asignación $S$ es: $val(S) =\displaystyle{\sum_{b^i_k\in B:\ S(b^i_k)} v^i_k}$.
!!!note: Proposición
Encontrar la asignación óptima $S^* = argmax_S(val(S))$ es **NP**-duro ([#Rothkopf]) e inaproximable ([#Sandholm2]).
Veamos cómo trasladar las CA a un modelo DisCOP. Supongamos que el agente $A_i$ tiene una oferta $b_i = (G_i , v_i)$. Para cada bien $g_j\in G_i$ , $A_i$ crea una variable local $g^i_j$ que modela el ganador del bien $g_j$. El dominio de esta variable está compuesto por los agentes interesados en el bien $g_j$ (aquellos cuyas pujas contienen $g_j$).
$A_i$ conecta todas las variables $g^i_j$ de su problema local con una relación $r_i$ que asigna $v_i$ sólo a la combinación de valores $(g^i_j = A_i , g^i_k = A_i , \dots)$ (la que asigna todos los bienes $g^i_j \in b_i$ a $A_i$), y $0$ a todas las demás combinaciones.
### Asignación de recursos
!!!def: Definición (Problema de Asignación de Sensores Distribuidos (SAP))
El **problema de la red de sensores distribuidos** consiste en ([#Bejar]):
- un conjunto de sensores compuesto por $n$ sensores: $S = \{s_1, s_2, \dots, s_n\}$.
- $m$ objetivos que deben ser rastreados: $T = \{t_1, t_2, \dots, t_m\}$.
Cada sensor tiene un determinado *alcance* (la distancia máxima que puede cubrir), y para rastrear con éxito un objetivo, al menos $3$ sensores deben percibir a ese objetivo (para que se puede aplicar la triangulación utilizando los datos procedentes de esos $3$ sensores). Se aplican las siguientes restricciones:
- un sensor sólo puede rastrear un objetivo a la vez;
- los sensores pueden comunicarse entre sí, pero no necesariamente cada sensor con todos los demás (el grafo de conectividad de los sensores no está totalmente conectado). Los $3$ sensores que rastrean un objetivo determinado deben ser capaces de comunicarse entre sí.
Podemos formalizar el problema como un DisCSP asignando un agente para cada objetivo: las variables son los sensores necesarios (tres variables por agente), y los valores de cada variable son los sensores que pueden rastrear ese objetivo (están dentro del alcance). Supongamos que tenemos un agente $A_i$ para cada objetivo $T_i$ a rastrear. Este agente tendría entonces $3$ variables que controlar: $s^i_1$, $s^i_2$, $s^i_3$; cada una de ellas representa un sensor que tiene que ser asignado para rastrear ese objetivo. El dominio de las variables de cada agente consiste en los sensores que realmente pueden *ver* el objetivo.
En esta representación del problema, tenemos dos tipos de restricciones:
- *Restricciones intra-agente*: (a) no se puede asignar el mismo valor a dos variables del mismo agente (un agente debe tener tres sensores diferentes que lo rastreen) y, (b) debe haber un enlace de comunicación entre cada dos sensores asignados a cada agente.
- *Restricciones entre agentes*: no se puede asignar el mismo valor a dos variables $s^i_k$ y $s^j_l$ de dos agentes cualesquiera $A_i$ y $A_j$ (un sensor puede rastrear un solo objetivo en un momento dado).
El problema es asignar los sensores a los objetivos de forma que se rastree el máximo número de objetivos. Alternativamente, cada objetivo puede producir una *recompensa* por ser rastreado, y entonces el problema es maximizar la suma de las recompensas.
!!!note: Proposición
SAP es **NP**-duro.
Es interesante observar que todas las restricciones de este problema (excepto las de *visibilidad*) son restricciones de exclusión mutua (típicas en los problemas de asignación de recursos).
# Pseudo-árboles y árboles DFS
Como hemos visto en el capítulo anterior, donde hemos analizado algunas soluciones a DisCSP, la forma en que se ordenan las variables/agentes para decidir el mecanismo de comunicación entre ellos es de una trascendencia fundamental para la eficiencia del algoritmo distribuido. Por ello, antes de entrar en la presentación de algoritmos para DisCOP, vamos a mostrar algunas definiciones y mecanismos para dar ordenaciones que aprovechan estructuras más elaboradas que las simples ordenaciones lineales.
!!!def: Definición (Pseudoárbol)
Un **pseudoárbol** asociado a un grafo $G$ es un árbol enraizado con los mismos nodos que $G$ y la propiedad de que nodos adyacentes en el grafo original caen en la misma rama del pseudoárbol.
!!!
Esta definición permite que el pseudoárbol sea un árbol enraizado con más aristas que el grafo original: impone una necesidad sobre nodos de $G$, pero no dice que deba ser satisfecha por medio de aristas de $G$.
La idea que añaden los pseudoárboles es que los nodos de $G$ situados en diferentes ramas se vuelven condicionalmente independientes. Por lo que es posible realizar búsquedas en paralelo en estas ramas independientes sabiend que no necesitaremos comunicación entre ellas. En concreto, si se empiezan a instanciar los nodos de arriba abajo (empezando por la raíz del pseudoárbol), entonces, para cada nodo, una vez instanciado, sus subárboles se vuelven completamente independientes, y pueden explorarse en paralelo.
## Árboles DFS
Un caso especial de pseudoárbol lo tenemos cuando se forma usando los recursos de $G$, es decir, cuando todas las aristas del pseudoárbol pertenecen al grafo original. Es fácil ver que esta clase especial puede ser generada por una búsqueda en profundidad del grafo (donde podemos elegir el nodo por el que comienza la búsqueda y el orden entre los sucesores de cada nodo), y por ello se denominan **árboles DFS**. Formalmente,
!!!def: Definición (Árbol DFS)
Un **Árbol DFS** de un grafo $G$ es un árbol enraizado, $T$, con los mismos nodos y aristas que $G$ y la propiedad de que nodos adyacentes en $G$ caen en la misma rama del árbol $T$.
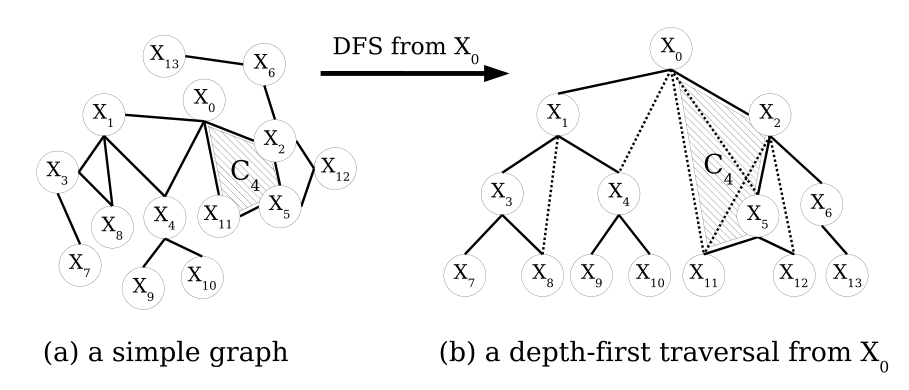
!!!
Los árboles DFS son, por tanto, una subclase de pseudoárboles. Sin embargo, hay pseudoárboles que no son árboles DFS.
Para DisCOP nos centraremos en las estructuras DFS, porque suponemos que sólo los agentes vecinos pueden comunicarse directamente. Además, se entiende bien cómo generar un árbol DFS de forma distribuida, mientras que está mucho menos claro para los pseudoárboles que no son árboles DFS. No obstante, la mayoría de los algoritmos pueden, en principio, funcionar en estructuras de pseudoárbol generales si se relaja la suposición de comunicación.
La figura anterior (ignorando las aristas punteadas) muestra un ejemplo de árbol DFS para un grafo concreto al que nos referiremos en el resto de esta sección. A los caminos del grafo que usan únicamente aristas del árbol se les llamará **caminos de árbol**. Un camino de árbol que conecta un nodo con uno de sus descendientes se llama **rama**. A las aristas de $G$ que no están en el árbol DFS (punteadas en la figura) las llamaremos **posteriores**. Por similitud con las variables de problemas CSP o COP, los nodos del grafo serán denotados por $X_i$.
!!!def: Definición (conceptos DFS)
Dado un árbol DFS enraizado, $T$, de un grafo $G$, para cada nodo $X_i$ del árbol, definimos:
- Los **hijos** ($C_i$) / **padres** ($P_i$) del nodo $X_i$: son los descendientes / ancestros de $X_i$ que están conectados a $X_i$ a través de una arista del árbol (por ejemplo, $P_4 = X_1$, $C_1 = \{X_3, X_4\}$).
- Los **pseudohijos** ($PC_i$) / **pseudopadres** ($PP_i$) del nodo $X_i$ son los descendientes / ancestros de $X_i$ que están conectados a $X_i$ a través de aristas posteriores ($PC_0 = \{X_4, X_5, X_{11}\}$, $PP_8 = \{X_1\}$). Nótese que $P_i \notin PP_i$.
- El **separador** ($Sep_i$) del nodo $X_i$ es el conjunto de todos los ancestros de $X_i$ que están conectados con $X_i$ o con descendientes de $X_i$ (por ejemplo, $Sep_3 = \{X_1\}$, $Sep_5 = \{X_0, X_2\}$ y $Sep_8 = \{X_1, X_3\}$); en otras palabras, dado un árbol DFS, $Sep_i$ es el conjunto mínimo de ancestros de $X_i$ cuya eliminación desconecta (separa) completamente el subárbol enraizado en $X_i$ del resto del problema. Para los árboles, $Sep_i = \{P_i\}$, para todo $X_i \in X$.
Cada nodo $X_i$ puede determinar fácilmente su separador $Sep_i$ como la unión de: (a) los separadores recibidos de sus hijos, y (b) sus padres y pseudopadres, menos él mismo. Formalmente,
$$Sep_i = (\bigcup_{X_j\in C_i} Sep_j) \cup P_i \cup PP_i-\{X_i\}$$
La **profundidad** de un árbol DFS es el número de nodos de su rama. Además, si consideramos un ordenamiento $o =\{X_1,\dots, X_n\}$ en los nodos de $G$, la **anchura inducida por $o$** en $G$ se define como:
!!!def: Definición (Anchura inducida)
Procesamos todos los nodos en el orden inverso de $o$. Al procesar un nodo, lo conectamos con todos sus vecinos que le preceden en la ordenación dada por $o$. La anchura del nodo actual viene dada por el número de estos vecinos que le preceden inducidos por la ordenación $o$. La anchura inducida por la ordenación $o$ es la mayor anchura inducida de cualquier nodo por la ordenación $o$.
Al considerar como ordenamiento el recorrido de los nodos de $G$ proporcionado por un determinado DFS, tenemos:
!!!def: Proposición
La anchura inducida de un grafo $G$ a lo largo de un DFS dado es igual al tamaño del mayor separador de cualquier nodo en el DFS.
!!!Tip:Demostración
Si procesamos los nodos de $G$ en el orden DFS inverso según la definición de anchura inducida, conectamos todos sus vecinos en $G$ que son sus ancestros en el DFS, es decir, conectamos su padre con todos sus pseudopadres. Si hacemos esto recursivamente en orden inverso al DFS, desde las hojas hasta llegar a la raíz, al final del proceso, para cada nodo tendremos una relación de vecindad (inducida) entre él y todos sus ancestros que estén conectados en G con él o cualquiera de sus hijos. Lo que significa que, utilizando la definición de anchura de un nodo, llegamos exactamente a la definición del separador del nodo. Por lo tanto, la anchura inducida del ordenamiento DFS es igual al tamaño del mayor separador de cualquier nodo en el DFS.
## Construcción distribuida
La generación de árboles DFS de forma distribuida es una tarea que ha recibido mucha atención, y hay muchos algoritmos disponibles. Nosotros veremos aquí uno que es similar al que se presenta en [#Cheung]. Podemos suponer que este procedimiento es ejecutado en una fase de preprocesamiento en la mayoría de los algoritmos que hacen uso de una optimización estática (los algoritmos que hacen uso de prioridades dinámicas suelen hacer uso de otros algoritmos para definir las prioridades iniciales). Después veremos que podemos ampliar este algoritmo con diferentes heurísticas para producir árboles DFS de mejor calidad.
~~~~none
Algoritmo de construcción de DFS para DisCOP.
Entrada: cada agente X_i conoce su entorno X_j ∈ N(X_i)
Salida: cada X_i etiqueta sus vecinos como P_i, PP_i, C_i, PC_i.
Procedimiento de Inicialización
1 Se elige un X_0 como raíz.
2 Todos los agentes ejecutan Paso_Token
Procedimiento Paso_Token (ejecutado por X_i)
Si X_i = X_0, entonces P_i = null; crea token DFS = ∅
3 si no, DFS = Maneja_Token_entrante()
4 DFS_i = DFS ∪ {X_i}
5 [Opcional: ordena N(X_i) de acuerdo a alguna heurística]
6 Para cada X_j ∈ N(X_i) hacer:
Si X_j no ha sido visitado todavía
7 añade X_j a C_i
8 envía DFS_i a X_j
9 espera DFS_j de X_j
10 elimina X_i de DFS_i y devuélvelo a P_i (subárbol completamente explorado)
Procedimiento Maneja_Token_entrante()
11 Espera mensaje entrante: X_j el remitente, marca X_j como visitado
Si es el primer mensaje DFS (X_j es mi padre) entonces:
12 P_i = X_j; PP_j = {X_k ̸= P_i | X_k ∈ N(X_i) ∩ DFS_jl}
si no
13 [Opcional: ordena los vecinos no visitados de acuerdo a alguna heurística]
Si X_j ∈ C_i (el mensaje viene de retorno de un hijo) entonces:
14 continuar con otros vecinos
15 si no: añadir X_j a PC_i (el mensaje viene de un pseudohijo)
~~~~
El algoritmo comienza con cada agente $X_i$ identificando su conjunto de vecinos, $N(X_i)$, como todos los demás agentes $X_j$ con los que $X_i$ comparte una relación (restricción). A continuación, cada agente etiqueta internamente a sus vecinos como no visitados. Uno de los agentes del grafo se designa como raíz, utilizando, por ejemplo, un algoritmo de elección de líder específica, o simplemente eligiendo al agente con el ID más bajo/más alto.
La raíz inicia entonces la propagación de un token, que es un mensaje único que circulará a todos los agentes del grafo, *visitándolos*. Inicialmente, el token sólo contiene el ID de la raíz. La raíz lo envía a uno de sus vecinos, y espera su regreso antes de enviarlo a cada uno de sus vecinos (aún) no visitados. Cuando un agente $X_i$ recibe por primera vez el token, marca al remitente como su padre. Todos los vecinos de $X_i$ contenidos en el token se marcan como pseudopadres de $X_i$ ($PP_i$).
Después, $X_i$ añade su propio ID al token y lo envía, a su vez, a cada uno de sus vecinos no visitados $X_j$, que se convierten en sus hijos. Cada vez que un agente recibe el token de uno de sus vecinos, marca al emisor como visitado. El token puede volver tanto de $X_j$ (el hijo al que $X_i$ lo ha enviado en primer lugar), como de otro vecino, $X_k$. En este último caso, significa que hay un ciclo en el subárbol, y $X_k$ se marca como pseudohijo.
Cuando todos sus vecinos están marcados como visitados, $X_i$ ha terminado de explorar todo su subárbol. A continuación, $X_i$ elimina su propio ID de la ficha, y envía la ficha de vuelta a su padre; el proceso ha terminado para $X_i$. Cuando la raíz ha marcado a todos sus vecinos como visitados, el proceso de construcción de la DFS ha terminado.
!!!def:Proposición
El algoritmo produce un DFS correcto que se ha construido de manera distribuida. Y produce $2 |E|$ mensajes de tamaño lineal, donde $|E|$ es el número de aristas del grafo.
!!!Tip
Debido al hecho de que cada nodo añade su ID al token cuando lo envía a sus hijos, y luego lo elimina cuando lo devuelve a su padre, la estructura de todo el problema permanece oculta para los agentes individuales. Cada agente sólo conoce su posición en el árbol, que viene dada por su conocimiento de su padre, hijos, pseudopadres y pseudohijos.
!!!Tip: Observación (Restricciones no binarias)
Las restricciones no binarias son tratadas correctamente de forma automática por el algoritmo anterior como resultado del hecho de que todos los agentes implicados en una restricción o relación (ya sea binaria o no binaria) se etiquetan entre sí como vecinos. El bucle de la línea 6 asegura que el primer agente implicado en una restricción no binaria, al recibir el token, lo pasará posteriormente a todos los demás agentes implicados en esa restricción, convirtiéndolos así en sus descendientes. Esto garantiza que no haya aristas cruzadas entre diferentes subárboles y que el DFS se construya correctamente. Por ejemplo, en la figura anterior, la zona sombreada muestra una restricción de 4 elementos, $\{X_0, X_2, X_5, X_{11}\}$, lo que implica que estos nodos son vecinos, y en el proceso de construcción del DFS aparecerán en la misma rama del árbol.
## Heurísticas
La complejidad de los algoritmos para DisCSP y DisCOP dependen del árbol DFS concreto del que se parta. En el caso de los algoritmos basados en la búsqueda lineal, la complejidad es exponencial en tiempo en la profundidad del árbol DFS. En cambio, los métodos de programación dinámica son exponenciales en tiempo y espacio en la anchura del árbol DFS. Por lo tanto, dependiendo del algoritmo que se vaya a utilizar, se querrá tener el árbol DFS de profundidad mínima o el árbol de anchura mínima. Sin embargo, se ha demostrado que encontrar cualquiera de ellos es un problema **NP**-duro. Normalmente, hay que conformarse con una aproximación del mejor árbol DFS, que puede obtenerse mediante algún proceso de generación heurística. El algoritmo de construcción de DFS visto puede parametrizarse con dos parámetros: el agente inicial (la raíz) y una función heurística que cada agente utiliza para decidir en cada paso a qué vecino no visitado enviará el siguiente token.
Ya existen varias heurísticas para generar buenos árboles DFS en el caso centralizado. Sin embargo, la aplicación de estas técnicas de forma distribuida puede no ser fácil, o incluso no ser factible.
### Heurísticas de poca profundidad
Se utilizan para generar árboles DFS orientados a algoritmos de búsqueda.
Aunque existen muchos algoritmos para generar árboles DFS de poca profundidad en el caso centralizado, no está claro cómo implementarlos de forma distribuida, y se ha trabajado poco en esta área. Chechetka y Sycara introdujeron en [#Chechetka] el primer algoritmo distribuido que construye un pseudoárbol utilizando una heurística diseñada para minimizar la profundidad del pseudoárbol. Aunque el algoritmo funciona bien, en general no produce árboles DFS, sino pseudoárboles, por lo que no vale para el caso que analizamos.
En realidad, el hecho de que exijamos árboles DFS en lugar de cualquier pseudoárbol significa que los algoritmos de búsqueda pueden ser arbitrariamente malos en comparación con los de programación dinámica. Para ver esto, consideremos un ejemplo sencillo de una red de restricciones en anillo con $n$ agentes. Cualquier ordenación DFS de un grafo de este tipo tendrá una profundidad $n$, lo que hace que los algoritmos de búsqueda se ejecuten en tiempo exponencial en $n$ (el tiempo de ejecución es $O(d^n)$). En cambio, un algoritmo de programación dinámica sólo sería exponencial en la anchura del DFS, que es 2 para un anillo, por lo que ofrece una aceleración exponencial (el tiempo de ejecución es $O(d^2)$).
### Heurísticas de poca anchura
Se utilizan para generar árboles DFS orientados a programación dinámica.
El objetivo de estos métodos es producir un DFS con la menor anchura inducida. En un entorno centralizado, las heurísticas más comunes para este problema son: grado máximo, conjunto de cardinalidad máxima, y *min-fill*. Como *min-fill* no produce en general ordenamientos de pseudoárboles (y mucho menos DFS), y es difícil de implementar en un entorno distribuido (porque requeriría la coordinación en cada paso entre todos los agentes restantes para decidir cuál debe ser considerado el siguiente en el ordenamiento de eliminación), nos centramos en describir adaptaciones distribuidas de las otras dos heurísticas:
1. **MCN: nodo más conectado** (también conocida como grado máximo). Funciona de la siguiente manera: el agente con el máximo número de vecinos se selecciona como raíz (los empates se rompen eligiendo el agente con el menor ID). Después, el proceso visita en cada paso a los agentes vecinos con el mayor número de vecinos (los empates se rompen de nuevo eligiendo al vecino con el menor ID). En concreto, el proceso se puede implementar cambiando el algoritmo anterior en dos partes: en el paso 1 cada agente transmite el número de sus vecinos, el agente mejor clasificado se elige como raíz; en el paso 5 cada agente ordena la lista de sus vecinos, los más conectados primero. El resto procede con normalidad.
2. **MCS: conjunto de cardinalidad máxima adaptado a los árboles DFS**. Funciona seleccionando algún agente como el primero en ser eliminado, y añadiéndolo al conjunto $S$ de agentes visitados. A continuación, se considera cada uno de los agentes que no están en $S$. El que tiene más vecinos ya en $S$ se selecciona para ser eliminado a continuación, y se coloca en el conjunto $S$. Los empates se rompen al azar (o por el ID del agente). El proceso se repite hasta que todos los agentes estén en $S$. Para adaptar esta idea al algoritmo de generación de DFS anterior, se sustituye el código de gestión de mensajes (líneas 11-15) por el siguiente proceso, que pretende simular la heurística MCS:
- Cada vez que un agente $X_i$ recibe un mensaje DFS de uno de sus vecinos:
- Selecciona a sus vecinos que no estén ni visitados ni en el contexto del token (son agentes aún no visitados, futuros hijos/pseudohijos).
- Pregunta a cada uno de ellos cuántos de sus vecinos están ya en el contexto del mensaje DFS.
- Envia el token junto al vecino que responda con el número más alto.
# Algoritmos para DisCOP
## Búsqueda Bactracking
Con pocas excepciones, la mayor parte del trabajo en optimización distribuida ha girado en torno a la extensión a un entorno distribuido de varias formas de búsqueda por backtracking ([#Bitner]) originalmente diseñadas para COP centralizado. En general, como hemos visto en el capítulo anterior, los algoritmos de búsqueda centralizada funcionan estableciendo un orden de las variables, y luego ejecutando una forma de búsqueda con backtracking basada en ese orden: se asignan a las variables valores que son compatibles con los valores elegidos para sus ancestros, y luego se avanza hacia la siguiente variable. Cuando para una variable no hay ningún valor que sea compatible con los valores elegidos para sus ancestros, se produce un backtrack. La asignación culpable de sus ancestros se denomina **nogood**. Para los algoritmos de satisfacción, la búsqueda continúa hasta que (a) se descubre un nogood vacío (es decir, no hay solución al problema), o (b) se descubre una instanciación completa que no contiene ningún conflicto. En el caso de los algoritmos de optimización, la búsqueda continúa hasta que se explora *lo suficiente* el espacio de búsqueda para poder inferir que se ha encontrado la solución óptima.
Para aumentar la eficiencia, se han desarrollado varios esquemas que intentan minimizar la porción del espacio de búsqueda que hay que visitar para demostrar que el algoritmo ya ha encontrado la solución óptima. El esquema más conocido es el de **Branch-and-Bound** (**BB**, [#Land]) de optimización centralizada:
1. En cuanto se obtiene una instanciación completa, la almacenamos como la mejor solución actual, y el coste de esta instanciación como un límite superior del coste que tolera el algoritmo.
2. Más adelante, durante la búsqueda, cada vez que se prueba un nuevo valor para una variable, se calcula el coste parcial acumulado hasta esa variable, y se le añade el coste incurrido por la nueva instanciación: Si este coste es mayor que el límite superior actual, se poda la asignación, ya que no puede conducir a una solución mejor que la mejor solución actual, y la búsqueda retrocede.
3. Siempre que encontremos una nueva instanciación completa que tenga un coste menor que la mejor solución actual, actualizaremos la mejor solución actual a la nueva, y el límite superior al coste de esta nueva solución.
Los algoritmos DisCOP suelen tratar de adaptar y ampliar sus homólogos centralizados a los entornos distribuidos, y se basan en los mismos principios: búsqueda por retroceso y algún esquema de límites para la poda. Sin embargo, como hemos comentado, es muy importante tener en cuenta que las medidas de rendimiento de los algoritmos distribuidos son radicalmente diferentes de las que se aplican a los centralizados. En concreto, si en la optimización centralizada el tiempo de cálculo es el principal cuello de botella, en la optimización distribuida es más bien la comunicación el factor limitante. Esta importante diferencia hace que el diseño de algoritmos eficientes de optimización distribuida sea una tarea no trivial que no consiste simplemente en adaptar los algoritmos centralizados para que funcionen de forma distribuida.
!!!Tip:Modelo de ejecución
Al igual que en los algoritmos para DisCSP, los algoritmos DisCOP se distinguen por ser síncronos o asíncronos. De manera informal:
- **Algoritmo Síncrono**: cada agente espera los mensajes que debe recibir de sus compañeros, y sólo después de haberlos recibido, comienza a realizar el cálculo y a enviar sus propios mensajes. Un modelo de ejecución síncrona garantiza que los agentes realicen sus cálculos basándose en la información relevante y más actualizada. Por lo tanto, se elimina la necesidad de realizar otro cálculo cuando llega un mensaje actualizado.
- **Algoritmo Asíncrono**: todos los agentes empiezan a realizar cálculos y a enviar mensajes incluso antes de haber recibido ningún mensaje de sus compañeros. A medida que llegan los mensajes, los incorporan a su cálculo y, si es necesario, envían sus propios mensajes actualizados. La ejecución asíncrona tiene la ventaja potencial de que los agentes no se quedan parados esperando mensajes cuando podrían realizar cálculos.
## Búsqueda Síncrona
### Branch and Bound Síncrono (SynchBB)
El algoritmo **SynchBB** fue el primer algoritmo completo para DisCOP, y fue propuesto por primera vez por Hirayama y Yokoo en [#Hirayama]. Es una versión simple y distribuida del esquema **BB** comentado anteriormente... tan simple, que SynchBB no utiliza un árbol DFS, sino un ordenamiento lineal de los agentes.
Después de establecer un orden (por ejemplo, lexicográfico), los agentes realizan una búsqueda síncrona de ramas y cotas. El proceso funciona como el algoritmo centralizado BB; sin embargo, los agentes, cada uno de ellos asociado a una única variable, no tienen acceso a las cotas globales superiores/inferiores de la calidad de la solución. Este problema se resuelve simplemente pasando estas cotas de un lado a otro junto con los mensajes de asignación de valores hacia adelante y los mensajes de backtrack hacia atrás.
Este algoritmo puede requerir que dos agentes/variables cualesquiera puedan comunicarse directamente, violando así la suposición de que sólo se permite comunicación entre vecinos directos. Además, se ha demostrado que es bastante ineficiente y que es fácilmente superado por esquemas más elaborados, pero al ser el primero y del que muchos toman ideas, es necesario al menos indicarlo.
### Búsqueda simple AND/OR
Los **espacios de búsqueda AND/OR** son un concepto muy potente para la búsqueda que fue introducido por Nilsson en [#Nilsson]. Posteriormente, Dechter y Mateescu ([#Dechter]) mostraron cómo los grafos AND/OR pueden capturar espacios de búsqueda para modelos de grafos generales que incluyen redes de restricciones y redes de creencias.
Los espacios de búsqueda AND/OR son una formalización de la idea de que la búsqueda en una estructura de (pseudo)árbol es potencialmente mejor que la búsqueda tradicional en órdenes lineales de variables. La razón es que, cuando se realiza en una estructura de (pseudo)árbol, la búsqueda puede hacerse en paralelo en distintas ramas del árbol, lo que da lugar a procesos de búsqueda que, en el peor de los casos, son exponenciales en cuanto a la profundidad del árbol (que suele ser menor que el número de variables). Por el contrario, los algoritmos de búsqueda tradicionales que operan sobre órdenes lineales de variables son exponenciales en tiempo en el número de variables. Por lo tanto, siempre es beneficioso realizar la búsqueda en árboles con poca profundidad en contraposición a los órdenes lineales de variables.
Hay diversos trabajos que usan esta idea en entornos centralizados ([#Dechter]). El Algoritmo **dAO-Opt** (**distributed And-Or Optimization**) que se muestra a continuación es una extensión simple y sincronizada de la búsqueda AND/OR para problemas de optimización distribuida (la notación que se usa en el algoritmo es la correspondiente a la dada en el apartado de pseudoárboles):
~~~~none
Algoritmo dAO-opt - Búsqueda Distribuida AO para optimización de coste.
dAO-opt(X,D,R):
Cada agente X_i hace:
Procedimiento EVAL: X_i espera mensaje EVAL(Sep_i) de P_i (salvo la raíz)
1 Cuando se recibe EVAL(Sep_i):
2 Para cada v_i ∈ dom(Xi) hacer:
3 coste(v_i) ← coste_local(v_i, Sep_i)
4 Para cada X_j ∈ C_i hacer:
5 enviar EVAL(Sep_{X_j}) a X_j
6 esperar las respuestas con mensaje COSTE
7 coste(v_i) = coste(v_i) + coste_{X_j}(v_i)
8 v*_i ← argmin_{v_i ∈ dom(X_i)} (coste(v_i))
9 Si X_i es la raíz entonces v*_i es el valor de la raíz de la solución óptima, y coste(v*_i) es el coste óptimo
10 Si no: enviar COSTE(coste(v*_i)) a P_i
~~~~
En el algoritmo, partimos de un orden preestablecido en forma de árbol. La raíz $X_r$ comienza el proceso de búsqueda asignándose un valor $v^0_r$ de su dominio, e informando a sus hijos de esta elección con un mensaje $EVAL(Xr = v^0_r)$. A continuación, cada uno de los hijos elige un valor para su variable, lo transmite a sus hijos, y así sucesivamente.
Cuando un agente $X_i$ recibe un mensaje $EVAL(Sep_i)$ de su padre, el mensaje incluye una asignación completa de todas las variables de $Sep_i$. A partir de esta asignación, $X_i$ puede evaluar, para cada uno de sus valores $v^j_i\in dom(X_i)$, aquellas funciones de utilidad que tiene con sus ancestros que están completamente instanciadas. En el caso de las funciones no binarias, $X_i$ limita esta evaluación sólo a aquellas relaciones cuyo ámbito no incluye a ninguno de sus descendientes; estas funciones ya están completamente instanciadas, y pueden ser evaluadas por $X_i$. Los costes correspondientes se denotan como $coste\_local(v^j_i ,Sep_i)$, para cada $v^j_i\in dom(X_i)$:
!!!def: Definición (Coste local)
Para cada agente $X_i$, denotamos por $coste\_local(v^j_i, Sep_i) = \sum_{r_i\in X_i} r_i(v^j_i, Sep_i)$, cuando $r_i$ está totalmente instanciado. Es el coste de sus funciones de utilidad y restricciones con sus ancestros cuando estos ancestros tienen asignados los valores como indica $Sep_i$ y $X_i = v^j_i$. Si la asignación $X_i = v^j_ i$ viola alguna de estas restricciones, entonces el coste es $\infty$.
Cuando los mensajes de $EVAL$ han llegado a las hojas, o en caso de un callejón sin salida (es decir, cuando un agente no puede encontrar un valor en su dominio que sea coherente con las asignaciones de sus antepasados), comienza el proceso de backtrack. Las hojas recorrerán sus valores, determinarán los mejores para la instanciación actual de sus ancestros y responderán con el mejor coste. Un agente sin salida responde con un coste infinito. Posteriormente, cuando un agente $X_i$ haya recibido mensajes de coste de todos sus hijos para su valor actual, probará el siguiente valor, informará a los hijos de su nueva asignación y esperará las respuestas de coste. Cuando se prueban todos sus valores, el agente elige el mejor (coste mínimo, o utilidad máxima, según hagamos minimización o maximización). A continuación, el agente comunica el coste correspondiente a su padre a través de un mensaje $COSTE$, y el padre comienza a recorrer sus valores, y así sucesivamente.
Cuando la raíz $X_r$ ha recorrido todos sus valores y ha recibido mensajes $COSTE$ para cada uno de ellos, puede elegir el mejor. El coste (utilidad) asociado al mejor valor de la raíz es el coste (utilidad) óptimo para todo el problema.
!!!Tip
Por ahora, este proceso sólo permite determinar el coste (utilidad) de la mejor solución, pero no necesariamente la solución en sí. La razón es que este sencillo esquema no realiza ningún tipo de almacenamiento en caché. Por lo tanto, cuando la raíz averigua cuál es su valor óptimo, y lo anuncia, sus hijos no saben cuáles eran sus correspondientes valores óptimos, y tendrán que volver a obtenerlos. Por tanto, hay otra fase de búsqueda descendente iniciada por la raíz, en la que cada agente anuncia su valor óptimo, y sus hijos vuelven a resolver sus subárboles en el contexto de los valores tomados por sus antecesores. Así, se vuelven a resolver subárboles cada vez más pequeños, con el fin de volver a obtener los valores óptimos de las raíces de estos subárboles (en el contexto de que los antecesores ya tienen asignados sus valores óptimos). Finalmente, el proceso llega a las hojas, y en este punto, se asignan a todos los agentes sus valores de la solución óptima.
El problema de redescubrir la solución es un problema que se da en todos los algoritmos de búsqueda distribuida que no hacen caché completo. Sin embargo, esto no ocurre en un algoritmo centralizado, ya que en ese caso *la mejor solución hasta el momento* puede ser almacenada, y posteriormente recuperada al final del proceso. Esta es otra complicación que hay que resolver para tener algoritmos de búsqueda distribuida eficientes.
!!!note: Proposición (complejidad de dAO-opt)
**dAO-opt** requiere un número de mensajes que es exponencial en la profundidad del árbol utilizado. El tamaño de los mensajes y los requisitos de memoria son lineales para cada agente.
Se hace evidente que es deseable encontrar árboles con baja profundidad, ya que la complejidad del peor caso de **dAO-opt** depende de este parámetro.
## Búsqueda Asíncrona: ADOPT
**ADOPT** (**Asynchronous Distributed OPTimization**, [#Modi]) es un mecanismo de propagación de cotas basado en backtracking. ADOPT fue el primer algoritmo descentralizado que garantizaba la optimalidad, al tiempo que permitía a los agentes operar de forma asíncrona.
!!!def
El algoritmo funciona de la siguiente manera:
1. Primero se crea la estructura DFS.
2. A continuación, se realiza una búsqueda descendente, utilizando la siguiente heurística de ordenación de valores: en cada momento, cada agente elige el valor con la cota inferior más pequeña.
3. Anuncia su elección a sus descendientes a través de mensajes de VALOR, y espera a que los mensajes de COSTE regresen de los hijos.
4. Cada agente suma los costes recibidos de sus hijos a la cota inferior del valor actual que toma el agente. Si hay otro valor en el dominio que tenga una cota inferior menor, el agente cambia su valor y el proceso se repite, refinando las cotas inferiores de forma iterativa.
ADOPT fue el primer algoritmo para DisCOP que podía encontrar la solución óptima, o una solución dentro de una distancia especificada por el usuario desde la óptima, utilizando sólo comunicación asíncrona localizada y espacio polinómico en cada agente. La comunicación es local en el sentido de que un agente no envía mensajes a todos los demás agentes, sino sólo a los agentes vecinos. ADOPT se basa en un único agente raíz para agregar cotas de costes globales y detectar la terminación. Aunque esta característica añade cierto grado de centralización al algoritmo, ADOPT también tiene muchas características distribuidas, como que todos los agentes realizan cálculos en paralelo. Por lo tanto, aunque ADOPT no es un algoritmo tan distribuido como podría serlo, tampoco es un algoritmo centralizado.
Podemos destacar los puntos fuertes de ADOPT como:
1. La idea principal de ADOPT es obtener asincronía permitiendo que cada agente cambie el valor de la variable siempre que detecte que existe la posibilidad de que alguna otra solución sea mejor que la que se está investigando en ese momento. Esta estrategia de búsqueda permite la computación asíncrona porque un agente no necesita información global para tomar sus decisiones locales: puede adelantarse y empezar a tomar decisiones sólo con información local. Debido a que esta estrategia de búsqueda permite abandonar las soluciones parciales antes de que se demuestre la suboptimidad, es posible que las soluciones parciales deban ser revisadas.
2. La segunda idea clave de ADOPT es reconstruir de forma eficiente las soluciones parciales consideradas anteriormente (utilizando sólo un espacio polinómico) mediante el uso de umbrales de retroceso, una tolerancia en el coste de la solución que evita el retroceso.
3. Por último, la tercera idea clave de ADOPT es proporcionar un mecanismo de detección de terminación integrado en el algoritmo: los agentes terminan cuando encuentran una solución completa cuyo coste está por debajo de su umbral de retroceso actual. La mayoría de los algoritmos de búsqueda asíncrona suelen requerir de un algoritmo de detección de la terminación por separado, lo que puede resultar problemático, ya que requiere el paso de mensajes adicionales.
La capacidad de ADOPT de ofrecer garantías de calidad y la detección de terminación incorporada conduce naturalmente a una técnica práctica para la aproximación acotando el error, proporcionando un algoritmo que garantiza la obtención de una solución cuya calidad está dentro de una distancia especificada por el usuario con respecto a la óptima, y normalmente en mucho menos tiempo del que se necesita para obtener la solución óptima. Encontrar la solución óptima de un DisCOP puede ser muy costoso para algunos problemas en los que no se dispone de recursos suficientes (por ejemplo, tiempo). Por lo tanto, la aproximación acotando el error cometido es una capacidad crucial necesaria para realizar compensaciones efectivas entre la calidad de la solución y el tiempo de cálculo en el mundo real. Hasta el momento de aparecer ADOPT, los enfoques que utilizaban la búsqueda incompleta para encontrar soluciones rápidamente carecían de la capacidad de proporcionar una garantía teórica sobre la calidad de la solución.
Los resultados experimentales muestran que ADOPT obtiene varios órdenes de magnitud de velocidad sobre SynchBB, el algoritmo completo más famoso para DisCOP. Los aumentos de velocidad se deben, en parte, a la nueva estrategia de búsqueda y, en parte, a la asincronía y el paralelismo que permite la estrategia de búsqueda. Además, aunque DisCOP es intratable en el peor de los casos, los experimentos demuestran que algunas clases de problemas presentan propiedades especiales en las que los algoritmos óptimos pueden funcionar muy bien. En particular, ADOPT es capaz de garantizar la optimalidad a bajo coste para problemas grandes cuando la red de restricciones es poco densa, una característica típica de muchos problemas del mundo real.
Dejamos el análisis e implementación detallada del algoritmo como trabajo.
# Referencias
[#Collin1]: Z. Collin, R. Dechter, and S. Katz. On the Feasibility of Distributed Constraint Satisfaction. In Proceedings of the 12th International Joint Conference on Artificial Intelligence, IJCAI-91, pages 318–324, Sidney, Australia, 1991.
[#Solotorevsky]: G. Solotorevsky, E. Gudes, and A. Meisels. Modeling and Solving Distributed Constraint Satisfaction Problems (DCSPs). In Proceedings of the Second International Conference on Principles and Practice of Constraint Programming (CP’96), pages 561–562, Cambridge, Massachusetts, USA, 1996.
[#Sycara]: K. Sycara, S. F. Roth, N. Sadeh-Koniecpol, and M. S. Fox. Distributed constrained heuristic search. IEEE Transactions on Systems, Man, and Cybernetics, 21(6):1446–1461, December 1991.
[#Yokoo1]: M. Yokoo, E. H. Durfee, T. Ishida, and K. Kuwabara. The distributed constraint satisfaction problem - formalization and algorithms. IEEE Transactions on Knowledge and Data Engineering, 10(5):673–685, 1998.
[#Schiex]: T. Schiex, H. Fargier, and G. Verfaillie. Valued constraint satisfaction problems: Hard and easy problems. In Proceedings of the 15th International Joint Conference on Artificial Intelligence, IJCAI-95, Montreal, Canada, 1995.
[#Gershman]: A. Gershman, A. Meisels, and R. Zivan. Asynchronous forward-bounding for distributed constraints optimization. In Proceedings of the 17th European Conference on Artificial Intelligence (ECAI-06), Riva del Garda, Italy, August 2006.
[#Modi]: P. J. Modi, W.-M. Shen, M. Tambe, and M. Yokoo. ADOPT: Asynchronous distributed constraint optimization with quality guarantees. AI Journal, 161:149–180, 2005.
[#Petcu]: A. Petcu and B. Faltings. DPOP: A scalable method for multiagent constraint optimization. In Proceedings of the 19th International Joint Conference on Artificial Intelligence, IJCAI-05, pages 266–271, Edinburgh, Scotland, Aug 2005.
[#Zhang]: W. Zhang and L. Wittenburg. Distributed breakout algorithm for distributed constraint optimization problems - DBArelax. In Proceedings of the International Joint Conference on Autonomous Agents and MultiAgent Systems (AAMAS-03), Melbourne, Australia, 2003.
[#Bertele]: U. Bertele and F. Brioschi. Nonserial Dynamic Programming. Academic Press, Inc., Orlando, FL, USA, 1972.
[#Kaplansky]: E. Kaplansky and A. Meisels. Distributed personnel scheduling - negotiation among scheduling agents. Annals of Operations Research, 2005. Accepted, July 2005.
[#Barrett]: A. Barrett. Autonomy architectures for a constellation of spacecraft. In Proc. of the 5th International Symposium on Artificial Intelligence, Robotics, and Automation for Space (i-SAIRAS-99), pages 291–296, Noordwijk, The Netherlands, 1999.
[#Tambe]: M. Tambe. Towards flexible teamwork. Journal of Artificial Intelligence Research, 7:83–124, 1997.
[#Chalupsky]: H. Chalupsky, Y. Gil, C. A. Knoblock, K. Lerman, J. Oh, D. V. Pynadath, T. A. Russ, and M. Tambe. Electric elves: Applying agent technology to support human organizations. In Proceedings of the Thirteenth Conference on Innovative Applications of Artificial Intelligence Conference, pages 51–58. AAAI Press, 2001.
[#Bejar]: R. Bejar, C. Fernandez, M. Valls, C. Domshlak, C. Gomes, B. Selman, and B. Krishnamachari. Sensor networks and distributed CSP: Communication, computation and complexity. Artificial Intelligence, 161(1-2):117–147, 2005.
[#Maheswaran]: R. T. Maheswaran, M. Tambe, E. Bowring, J. P. Pearce, and P. Varakantham. Taking DCOP to the real world: Efficient complete solutions for distributed multi-event scheduling. In AAMAS-04, 2004.
[#Vries]: S. de Vries and R. V. Vohra. Combinatorial auctions: A survey. INFORMS Journal on Computing, 15(3):284–309, 2003.
[#Ostwald]: J. Ostwald, V. Lesser, and S. Abdallah. Combinatorial Auction for Resource Allocation in a Distributed Sensor Network. The 26th IEEE International Real-Time Systems Symposium, (RTSS’05), pages 266–274, December 2005.
[#Walsh]: W. E. Walsh and M. P. Wellman. A market protocol for decentralized task allocation. In ICMAS ’98: Proceedings of the 3rd International Conference on Multi Agent Systems, page 325, Washington, DC, USA, 1998. IEEE Computer Society.
[#Sandholm]: T. Sandholm, S. Suri, A. Gilpin, and D. Levine. CABOB: A fast optimal algorithm for combinatorial auctions. In Proceedings of the 17th International Joint Conference on Artificial Intelligence, IJCAI-01, pages 1102–1108, 2001.
[#Fujita]: S. Fujita, S. Tagashira, C. Qiao, and M. Mito. Distributed branch-and-bound scheme for solving the winner determination problem in combinatorial auctions. In AINA ’05: Proceedings of the 19th International Conference on Advanced Information Networking and Applications, pages 661–666, Washington, DC, USA, 2005. IEEE Computer Society.
[#Narumanchi]: M. V. Narumanchi and J. M. Vidal. Algorithms for distributed winner determination in combinatorial auctions. In LNAI volume of AMEC/TADA. Springer, 2006.
[#Rothkopf]: M. H. Rothkopf, A. Pekec, and R. M. Harstad. Computationally manageable combinational auctions. Manage. Sci., 44(8):1131–1147, 1998.
[#Sandholm2]: T. Sandholm. Algorithm for optimal winner determination in combinatorial auctions. Artif. Intell., 135(1-2):1–54, 2002.
[#Bitner]: J. R. Bitner and E. M. Reingold. Backtrack programming techniques. Communications of the ACM, 18(11):651–656, 1975.
[#Nilsson]: N. J. Nilsson. Principles of Artificial Intelligence. Morgan Kaufmann, 1980.
[#Dechter]: R. Dechter and R. Mateescu. AND/OR search spaces for graphical models. Artificial Intelligence, 2006.
[#Land]: A. H. Land and A. Doig. An automatic method for solving discrete programming problems. Econometrica, 28:497–520, 1960.
[#Hirayama]: K. Hirayama and M. Yokoo. Distributed partial constraint satisfaction problem. In Principles and Practice of Constraint Programming, pages 222–236, 1997.
[#Cheung]: T.-Y. Cheung. Graph traversal techniques and the maximum flow problem in distributed computation. IEEE Trans. Software Eng., 9(4):504–512, 1983.
[#Chechetka]: A. Chechetka and K. Sycara. A decentralized variable ordering method for distributed constraint optimization. Technical Report CMU-RI-TR-05-18, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, May 2005.