**SVRAI**
Introducción a la Lógica
De la Lógica Proposicional a la Lógica de Primer Orden
En esta entrada vamos a intentar dar un curso acelerado (aceleradísimo) acerca de **Lógica Proposicional** y **Lógica de Primer Orden** y de qué forma se pueden automatizar algunos de los problemas más habituales que se presentan dentro de ella. Debido a que es un curso acelerado, no se debe buscar aquí una formalización exhaustiva acerca del tema, sino una aproximación intuitiva a cuáles son los fundamentos, los problemas que resuelven, y algunos de los algoritmos más habituales para automatizar las soluciones que se pueden dar a los mismos . Si el lector sabe algo de lógica lo más probable es que estas notas no le sirvan de mucho, encuentre muchas carencias e incluso alguna *mentira piadosa* (aunque prefiero llamarla *atajo*).
Para una visión más completa de la lógica, se puede visitar el material del curso [Lógica Informática](http://www.cs.us.es/cursos/liti/) que se imparte en diversos grados de la E.T.S. Ingeniería Informática de la Universidad de Sevilla, así como las referencias bibliográficas en ellos.
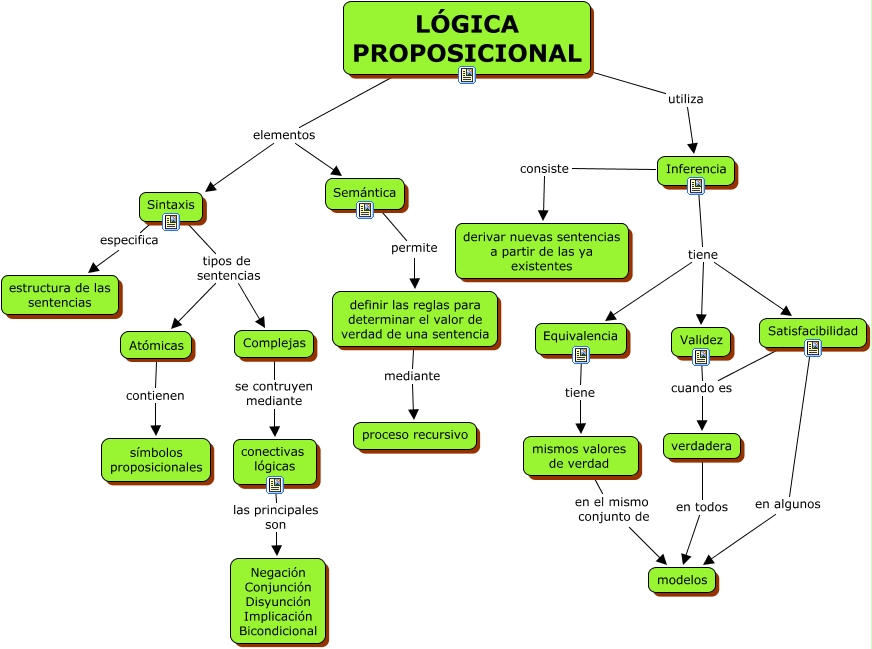
# Lógica Proposicional
¿Qué es la Lógica Proposicional? Antes de responder a esta pregunta, vamos a definir un poco el contexto en el que nos moveremos: qué es la lógica en general.
La **Lógica** es la rama del conocimiento que se encarga de estudiar las formas en que se pueden inferir verdades de una forma válida. La visión matemática de la Lógica (lo que se llama la **Lógica Matemática**) añade toda la capa de formalismo necesaria para disponer de un lenguaje adecuado y de los métodos precisos para que este estudio tenga un soporte de validez universal. En este sentido, se pueden dar diversos formalismos para afrontar este gran problema de la inferencia válida, y la **Lógica Proposicional** fue, posiblemente, el primer intento serio al que se dio forma, por allá en tiempos de los famosos griegos atenienses.
Todos estos sistemas intentan, de una u otra forma enfrentarse al problema de poder *asegurar cuándo, dada una base de conocimientos que se suponen ciertos, podemos asegurar que una afirmación es necesariamente cierta*... de forma coloquial, cuándo podemos deducir que esta última afirmación se deduce de los hechos observados (o supuestos). En particular, la Lógica Proposicional (que a partir de ahora notaremos abreviadamente como **LP**) se enfrenta a este problema definiendo:
1. De qué forma se pueden representar los hechos y afirmaciones; es decir, dando un lenguaje formal.
2. Qué entendemos por *afirmación cierta*.
3. Qué reglas podemos utilizar para garantizar la corrección de las deducciones que seamos capaces de obtener.
En el caso de la LP, las expresiones que podemos escribir con su lenguaje pueden tener dos posibles valoraciones: **verdad** o **mentira** (que, habitualmente, notaremos respectivamente por $V$ y $F$, o $1$ y $0$), y permiten usar los siguientes símbolos para poder expresar las afirmaciones del mundo:
1. Un conjunto infinito (pero numerable) de símbolos, que llamaremos **variables proposicionales**: $p$, $q$, $r$, $s$, ..., $p_1$, $p_2$,...
2. Una serie de conectivas que permiten combinar esos símbolos de forma adecuada: $\neg$, $\vee$, $\wedge$, $\rightarrow$ y $\leftrightarrow$, que se corresponden, respectivamente, con la **negación**, **disyunción** (...*o*...), **conjunción** (...*y*...), **implicación** (o *si ... entonces...*), y **doble implicación** (o *si y sólo si*).
3. Un par de **símbolos auxiliares**, $($ y $)$, para facilitar la escritura de las expresiones.
Evidentemente, no vamos a admitir como correcta cualquier combinación de los símbolos anteriores, y llamaremos **fórmulas** a aquellas expresiones que sí sean correctas en nuestro sistema.
!!!Tip
Por ejemplo: $(p \rightarrow q) \vee (\neg q \wedge r)$ es una fórmula correcta, mientras que $p \neg \wedge q$ no lo es).
Se puede dar una definición formal de qué es una fórmula (es decir, una expresión que está correctamente escrita) y qué no lo es, pero con la idea intuitiva es suficiente para este curso acelerado. Basta tener en cuenta que una expresión es una fórmula si se puede construir usando las conectivas anteriores usando las variables proposicionales. De esta forma, las variables proposicionales representarán las afirmaciones atómicas del mundo real (o del que estamos formalizando), es decir, aquellas que no pueden ser descompuestas en afirmaciones más pequeñas; y las otras fórmulas representarán afirmaciones compuestas.
De igual forma, podemos definir formalmente cuándo una fórmula es una subfórmula de otra.
El significado de las conectivas es el esperado en el lenguaje natural, aunque para determinar sin lugar a dudas su significado es habitual dar las tablas de verdad de las conectivas en función de la veracidad de las variables (o subfórmulas) que intervienen:
| $p$ | $q$ | $\neg\ p$ | $\neg\ q$ | $p\land q$ | $p\lor q$ | $p\rightarrow q$ | $p\leftrightarrow q$ |
| ---- | ---- | --------- | --------- | ---------- | --------- | ---------------- | -------------------- |
| $1$ | $1$ | $0$ | $0$ | $1$ | $1$ | $1$ | $1$ |
| $1$ | $0$ | $0$ | $1$ | $0$ | $1$ | $0$ | $0$ |
| $0$ | $1$ | $1$ | $0$ | $0$ | $1$ | $1$ | $0$ |
| $0$ | $0$ | $1$ | $1$ | $0$ | $0$ | $1$ | $1$ |
Observa que las variables proposicionales no tienen un valor fijo de verdad, sino que, como su nombre indica, son variables que pueden tomar cualquiera de los dos valores posibles. Cuando tenemos una fórmula y prefijamos los valores de las variables que intervienen en ella, decimos que tenemos una **valoración**, **asignación**, o **interpretación**. Aplicando de forma iterada las reglas de la tabla anterior sobre la construcción de una fórmula, obtener el valor de verdad de la fórmula completa.
!!!Tip
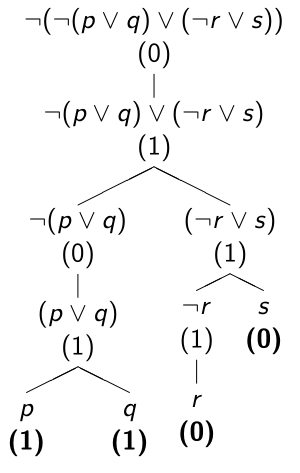
Por ejemplo, si la valoración $v$ asigna $v(p)=v(q)=1,\ v(r)=v(s)=0$, entonces el valor de $\neg(\neg(p\lor q)\lor (\neg r\lor s))$ es $1$, ya que:
A pesar de que la Lógica Proposicional presenta claras limitaciones expresivas y no puede reflejar fielmente muchas de las afirmaciones que podemos hacer en sistemas un poco más ricos, suele ser más que suficiente para muchísimos problemas de la vida real, por lo que sigue siendo útil en campos como el de la Inteligencia Artificial. Además, muchos de los métodos que se utilizan en lógicas más potentes (como la **Lógica de Primer Orden**, la **Lógica Difusa**, etc.) son extensiones de los métodos que se han definido para la Lógica Proposicional, por lo que su estudio en profundidad está más que justificado.
## Qué significa que una fórmula se pueda deducir de un conjunto de fórmulas
Una vez que hemos explicitado el lenguaje que usamos para formalizar las afirmaciones, y fijado lo que entendemos por su significado (de verdad o falsedad), es el momento de formalizar qué entendemos por **inferir de forma válida**.
- Dada una valoración, $v$, diremos que una fórmula, $F$, es **válida** en $v$ si el valor de verdad de $F$ con esa valoración es $1$, $v(F)=1$, y lo notaremos $v\models F$.
- Decimos que $F$ es una **Tautología** si siempre es válida, sea cual sea la valoración considerada.
- Decimos que es **Insatisfactible** (o una **Contradicción**) cuando nunca es válida, y decimos que es **Satisfactible** si es válida al menos una vez.
Los mismos conceptos se pueden aplicar a conjuntos de fórmulas, y no solo a fórmulas aisladas (en este caso, es satisfactible si existe una valoración que hace simultáneamente válidas a todas las fórmulas del conjunto).
!!!Tip
Por ejemplo, la fórmula $p\vee \neg p$ es una tautología, mientras que la fórmula $p\rightarrow q$ es satsifactible porque existen valoraciones que la hacen válida, pero no es tautología porque no lo hacen todas.
Además, **tenemos un método automático para saber si una fórmula es satisfactible**, **tautología** o **insatisfactible**, basta hacer la tabla de verdad de la fórmula y verificar si en el resultado hay algún $1$, si todos son $1$, o si todos son $0$ (respectivamente). El problema evidente es que es un proceso muy laborioso hacer la tabla de verdad de la fórmula cuando el número de variables que intervienen es alto (algo que suele ocurrir en los problemas del mundo real que son interesantes), ya que si tenemos $n$ variables en la fórmula, necesitaremos una tabla de verdad con $2^n$ casos distintos.
Aunque esta no es la entrada adecuada para exponer este problema, es obligatorio decir aquí que el problema de saber si una fórmula es satisfactible (que se denomina **SAT**) cae dentro de los que se denominan problemas **NP**... esencialmente, aquellos problemas para los que se conoce solución, pero es tan mala desde el punto de vista de los recursos que necesitamos para resolverlos (en tiempo o en espacio) que son **intratables** desde un punto de vista práctico cuando el tamaño del problema (el tamaño de la fórmula) es grande. Es más, no solo es NP, sino que además es **NP-completo**, lo que significa que está entre los más complejos de los más complejos. Cuidado que no estamos diciendo que no tengan solución más sencilla, sino que ahora mismo no se conoce una solución sencilla, solo soluciones malas (la idea general es que no existen esas soluciones buenas para este tipo de problemas, aunque todavía no hemos sido capaces de probarlo). Por ello, las soluciones que veremos más adelante relacionadas con SAT conseguirán facilitar la solución en algunos casos, pero nunca serán suficientemente buenas en todos los casos como para considerarlas óptimas.
Ahora ya podemos decir qué entendemos por consecuencia lógica que, como veremos, y la intuición dice, está intimamente relacionado con la idea de implicación:
*Diremos que una fórmula, $F$, es **consecuencia lógica** de un conjunto de fórmulas, $U=\{F_1,\dots,F_n\}$, y lo notaremos por $U\models F$, si se verifica que la fórmula $F_1\wedge \dots \wedge F_n \rightarrow F$ es una tautología.*
Como hemos dicho, la idea fundamental es la intuición de que la consecuencia lógica se relaciona, obviamente, con la implicación. Pero además, se puede probar (aunque no lo haremos) que *la definición anterior es equivalente a decir que el conjunto $\{F_1,\dots,F_n,\neg F\}$ es insatisfactible (una contradicción)*, que viene a reflejar el método habitual de probar que algo es consecuencia lógica por medio de la **reducción al absurdo** (si suponemos lo contrario, llegamos a una contradicción).
Al reducir la consecuencia lógica a comprobar una tautología o una satisfactibilidad, los métodos que tengamos para estos problemas podrán ser aplicados directamente para poder resolver el problema de la inferencia. Por tanto, ya tenemos un método, el de las tablas de verdad, para resolverlo... pero es un método demasiado primitivo e ineficiente para lo que buscamos, así que en lo que sigue nos orientaremos a buscar algunos otros métodos más elegantes, y sobre todo que nos proporcionen un mayor control para adaptarnos a las características particulares de la fórmula.
## Formas Clausales
Los métodos que vamos a ver aquí se podrán aplicar a fórmulas que estén escritas de una cierta forma, que se llama **forma clausal**. Para ello, definimos primero qué entendemos por un **literal**, que será una variable proposicional o la negación de una variable proposicional (por ejemlo, $p$, $\neg p$,...). En general, si tenemos que $L$ es un literal, notaremos por $L^c$ al literal contrario.
Una fórmula se dice que está en **forma clausal** (también llamada **Forma Normal Conjuntiva**) si es conjunción de disyunciones de literales, es decir, si $L_{ij}$ son literales, entonces:
$$F = (L_{11}\vee \dots \vee L_{1n_1}) \wedge (L_{21}\vee \dots \vee L_{2n_2}) \wedge \dots \wedge (L_{m1}\vee \dots \vee L_{mn_m})$$
!!!Tip
Por ejemplo: $(p \lor q \lor \neg r) \land (\neg p \lor \neg q) \land (q\lor r)$
Lo interesante es que se puede probar que cualquier fórmula se puede convertir en otra equivalente (es decir, que "dice" lo mismo, que tiene la misma tabla de verdad) expresada en forma clausal (o normal conjuntiva), por lo que los métodos que veamos a continuación se pueden aplicar a cualquier fórmula, siempre y cuando se transforme previamente a esta forma.
En realidad, debido a que la fórmula se ha expresado como una conjunción de disyunciones, podemos considerar que estamos trabajando con un conjunto de $m$ disyunciones, a cada disyunción se le llama **claúsula**. Por ello, podemos hablar de la forma clausal de una fórmula o de un conjunto de fórmulas, que pasaría a ser:
$$F = \left\{\{L_{11},\dots, L_{1n_1}\},\ \{L_{21},\dots,L_{2n_2}\},\dots,\{L_{m1},\dots,L_{mn_m}\}\right\} $$
Aunque no lo vamos a usar, también se puede escribir cualquier fórmula en **Forma Normal Disyuntiva**, es decir como una disyunción de conjunciones.
Las leyes habituales que nos permiten transformar una fórmula cualquiera en una equivalente en Forma Normal Conjuntiva (o Forma Normal Disyuntiva) son:

## Un algoritmo sencillo de satisfactibilidad: DPLL
**DPLL** es un algoritmo para decidir la satisfactibilidad de una fórmula (o conjunto de fórmulas) a partir de su forma clausal. Fue propuesto en 1960 por Davis y Putnam, y posteriormente refinado en 1962 por Davis, Logemann y Loveland (de ahí el nombre completo del algoritmo, DPLL). Este algoritmo es la base de la mayoría de los programas que resuelven el problema SAT y que se usan en entornos profesionales.
El **algoritmo DPLL** consta de dos partes bien diferenciadas que se van alternando en caso de necesidad:
1. Propagación de unidades,
simplifica el conjunto de cláusulas sobre el que se trabaja. Se elige una cláusula unitaria $L$ y se aplican consecutivamente las dos reglas siguientes (y se repite mientras queden cláusulas unitarias):
1. **Subsunción unitaria**. Se eliminan todas las cláusulas que contengan el literal $L$ (incluida la propia cláusula $L$).
2. **Resolución unidad**. Se elimina el literal complementario, $L^c$ de todas las cláusulas.
2. **División**, si no hay unidades que propagar en el conjunto actual, $S$, se elige un literal $L$ que aparezca en una de las cláusulas que permanecen y se consideran por separado los conjuntos de cláusulas: $S\cup \{L\}$ y $S\cup \{L^c\}$. A continuación aplicamos recursivamente el procedimiento a ambos conjuntos (que ya tienen las cláusulas unitarias que acabamos de introducir).
El algoritmo va ramificando el proceso y cada rama puede ser una solución al problema de la satisfactibilidad. Si en una rama aparece una contradicción (una cláusula unitaria y su cláusula complementaria de forma simultánea), esa rama no proporciona una solución, pero podría haber otra rama que sí lo hiciera. Si en una rama no aparece una contradicción, esa rama proporciona una valoración que hace satisfactible la forma clausal original. Si todas las ramas son contradictorias, la forma clausal original es una contradicción.
!!!Tip
Veamos un ejemplo de cómo aplicar este algoritmo:

En el ejemplo anterior, la rama derecha proporciona un modelo ($p=0,\ q=0,\ r=1$), por lo que la fórmula es satisfactible; mientras que las ramas izquierdas llegan a contradicción (ya que requieren que sean simultáneamente ciertas $r$ y $\neg r$) y no proporcionan modelos.
En cierta forma, este algoritmo es como el método habitual para resolver un sudoku, si tenemos ya algunos números seguros, su conocimiento se propaga a través del sudoku y nos permite asegurar más posiciones, y si llegamos a un callejón sin salida lo más normal es hacer suposiciones acerca de alguna de las casillas, valorando cómo evoluciona el puzzle para cada uno de sus posibles valores.
## Resumen de la Metodología
En resumen, si queremos resolver un problema habitual de saber si una cierta fórmula es consecuencia lógica (la podemos deducir) de un conjunto de fórmulas (hipótesis), formalmente, $\{F_1,\dots,F_n\}\models F$, los pasos a seguir serían:
1. Convertimos el problema en **verificar si $\{F_1,\dots,F_n,\neg F\}$ es satisfactible o no**, es decir, si somos capaces de encontrar un modelo para esas fórmulas o no.
2. **Pasamos cada una de esas fórmulas a forma clausal** (FNC) aplicando las reglas habituales para ello (ley distributiva, asociativa, de Morgan, etc). Podemos hacerlo por separado para cada fórmula y después simplemente consideramso el conjunto de todas las cláusulas obtenidas, cada fórmula dar un conjunto de cláusulas: $\{C_1,\dots,C_m\}$.
3. **Aplicamos DPLL o Resolución** al conjunto de cláusulas obtenido.
4. **Si encontramos un modelo** (en **DPLL**, una de las ramas obtiene una solución que no es contradicción; en **Resolución**, no somos capaces de encontrar la cláusula vacía), **entonces la consecuencia lógica NO es cierta**.
5. **Si no encontramos un modelo** (en **DPLL**, todas las ramas llegan a una contradicción; en **Resolución**, encontramos una cadena de resolventes que llegan hasta la cláusula vacía), **entonces la consecuencia lógica SÍ es cierta**.
## Algunas consideraciones finales: sobre la automatización
Aunque en general los algoritmos que existen para obtener nuevos resultados matemáticos no son automatizables (es decir, no se pueden programar en una máquina), el caso de la lógica proposicional, con todas sus limitaciones, sí que se puede automatizar. Ya vimos que el método más directo, y el más incómodo, para ello es el de la creación de la tabla de verdad. En esta entrada hemos visto algunos otros algoritmos que son fácilmente implementables (apenas usando algunas estructuras de listas o similares) y que pueden resultar más recomendables en caso de querer disponer de una implementación práctica.
A pesar de todo, no debemos olvidar que el problema que está detrás es **SAT**, y que es un problema **NP**-completo, por tanto no debemos poner nuestras esperanzas en conseguir algoritmos que rebajen el problema de la inferencia (ni siquiera en la Lógica Proposicional) y que lo convierta en un problema tratable para todos los casos, y nos conformamos con obtener métodos que sean suficientemente buenos como para poder atacar problemas con gran número de variables en muchos casos.
# Lógica de Primer Orden
Pese a las virtudes que ofrece un sistema de representación y razonamiento formal como la Lógica Proposicional (LP), esta puede no ser apropiada para expresar ciertos tipos de conocimiento. Por ejemplo, una sentencia tan sencilla como:
*Algunas máquinas son inteligentes*
solo dispone de una posible representación en LP, como variable proposicional, ya que es una afirmación atómica, perdiendo el grano fino que permita extraer, y reutilizar, un mayor conocimiento de su estructura. Si representamos esta sentencia por una variable proposicional, el sistema no será capaz de relacionar su contenido con una afirmación similar pero que da una información bien distinta:
*Las máquinas son inteligentes*
Este tipo de carencias, y muchas otras que surgen cuando intentamos modelar una información más rica, es la que nos lleva a la conclusión de que LP puede que no sea suficientemente expresiva para modelar cierto tipo de afirmaciones y razonamiento. Parte del problema que muestra LP es que no tiene capacidad para diferenciar propiedades en familias de elementos de un dominio: o bien habla de objetos particulares que tienen una descripción propia (un nombre que los identifica), o habla de propiedades del dominio completo como una unidad. No tiene capacidad de **ajuste fino**.
La Lógica de Primer Orden (LPO) viene a solucionar este tipo de problemas:
- Permite hacer cuantificación sobre los objetos de un dominio, por ejemplo, puede expresar cosas como: *Todas las máquinas son inteligentes*, *Algunas máquinas funcionan correctamente*, etc.
- Permite representar propiedades de los objetos particulares del dominio por medio de predicados y funciones.
- Permite trabajar con subconjuntos de objetos que pueden venir caracterizados por propiedades que se describen por medio de propiedades y funciones.
!!!Tip
Con el fin de aterrizar las ideas que vamos a introducir aquí, trabajaremos a lo largo de esta entrada con la formalización de la siguiente base de conocimientos acerca del mundo romano:
- Marco era pompeyano.
- Todos los pompeyanos eran romanos.
- Cada romano, o era leal a César, o le odiaba.
- Todo el mundo es leal a alguien.
- La gente sólo intenta asesinar a aquellos a quienes no es leal.
- Marco intentó asesinar a César.
- Todo pompeyano es leal a su padre.
Para ello, formalmente, un LPO, $L$, está compuesto por los siguientes elementos (lo que se denomina **sintaxis** en el ámbito de la definición de lenguajes formales):
- Un conjunto, finito o numerable, de símbolos de constantes para designar objetos: $C=\{c_1,c_2,\dots\}=\{a,b,c,\dots\}$ (no tenemos porqué tener designadores para todos los objetos del mundo modelado, quizás solo de algunos de ellos).
En el ejemplo anterior, objetos (individuos) como César y Marco necesitarían de símbolos específicos para poder referrirnos a ellos y expresar las afirmaciones en las que intervienen. Así pues, en nuestro lenguaje tomaremos $C=\{{\bf Marco}, {\bf Cesar}\}$.
- Un conjunto, finito o numerable, de símbolos para designar funciones: $F=\{f_1,f_2,\dots\}=\{f,g,h,\dots\}$ (cada función tiene una aridad propia, que indica el número de argumentos que recibe como entrada).
De nuevo, en el ejemplo anterior encontramos una función que asocia objetos a objetos, en este caso, asociada al concepto padre, que denotaremos por $f$, por lo que $F=\{f\}$, y para un objeto del mundo, por ejemplo, $Marco$, $f(Marco)$ representa a su padre.
- Un conjunto, finito o numerable, de símbolos para designar predicados: $P=\{P_1,P_2,\dots\}=\{P,Q,R,\dots\}$ (cada predicado tiene una aridad propia, que indica el número de objetos que relaciona).
En este caso, disponemos de varios predicados en el ejemplo que necesitamos formalizar, concretamente: $P(a)$ para decir que $a$ es pompeyano, $R(a)$ para expresar que $a$ es romano, $L(a,b)$ para indicar que $a$ es leal a $b$, $O(a,b)$ para indicar que $a$ odia a $b$, $IA(a,b)$ para indicar que $a$ intentó asesinar a $b$.
Observa que hablamos de *símbolos*, porque estamos definiendo un lenguaje, pero lo hacemos desde un punto de vista completamente formal, sin preocuparnos por el significado de lo que podamos escribir en él. Eso lo veremos más adelante en lo que podríamos denominar la **semántica** del lenguaje, que depende del uso que se le dé.
Además de estos elementos, un LPO necesita también otros símbolos que le permitan componer fórmulas y expresiones más complejas, y que son, esencialmente, una extensión de los mismos símbolos que usábamos para la LP:
1. $\neg$, $\wedge$, $\vee$, $\rightarrow$, $\leftrightarrow$: conectivas lógicas usuales y con el mismo uso que se le dio en LP.
2. $=$: un predicado especial para la igualdad. No es obligatorio, pero si lo añadimos, significa la igualdad habitual en la que $a=b$ si y sólo si $a$ y $b$ son el mismo objeto.
3. $V=\{x_1, x_2, \dots\}=\{x,y,z,\dots\}$: un conjunto numerable de variables con las que podemos representar objetos del mundo que estamos describiendo.
4. $\exists$, $\forall$: cuantificadores existencial y universal, habituales en la formalización matemática estándar que, en combinación con el uso de variables, permiten extender las propiedades particulares que podemos referenciar en objetos del mundo a propiedades de conjuntos de objetos.
5. $($ $,$ $)$: símbolos de puntuación auxiliares para facilitar la escritura y lectura de las expresiones que escribamos.
!!!Tip
Una formalización de las sentencias anteriores sería:
- $P({\bf Marco})$
- $\forall x\, ( P(x)\rightarrow R(x))$
- $\forall x\, (R(x)\rightarrow (L(x,{\bf Cesar})\vee O(x,{\bf Cesar}))$
- $\forall x\,\exists y\, L(x,y)$
- $\forall x\,\forall y\, (IA(x,y)\rightarrow \neg L(x,y))$
- $IA({\bf Marco},{\bf Cesar})$
- $\forall x\, (P(x)\rightarrow L(x, f(x)))$
Con este aparato, podemos definir formalmente cómo se escriben las expresiones correctas en este lenguaje, pero no nos vamos a centrar en tanto detalle (lo puedes encontrar en los apuntes oficiales de la asignatura de Lógica Informática), ya que su uso habitual en disciplinas de estudio conocidas (como matemáticas y física) nos proporciona suficientes ejemplos como para que podamos diferenciar las expresiones válidas de las no válidas sin posibilidad de error y sin necesidad de una farragosa definición formal. Lo único importante, porque lo usaremos más adelante, es diferenciar entre los tipos de expresiones que podemos construir:
- Aquellas expresiones que se identifican con posibles objetos se denominan **términos**, y están formadas a partir de constantes para hablar de objetos específicos, variables para hablar de objetos genéricos, y funciones aplicadas a otros términos más pequeños.
!!!Tip
En el ejemplo anterior, ${\bf Marco}$, $f({\bf Marco})$, $f(f({\bf Cesar}))$, $f(x)$, etc. son términos.
- Las expresiones que se identifican con afirmaciones sobre los objetos se denominan **fórmulas**, y están formadas a partir de predicados sobre términos, y construcciones lógicas de estos predicados (conjunciones, implicaciones, cuantificaciones, etc.).
!!!Tip
La formalización de las sentencias anteriores son ejemplos de fórmulas.
Observa que los LPO hablan de objetos, propiedades y funciones. Lo interesante es cuando estas expresiones se usan para hablar de mundos formados por objetos, con propiedades y funciones que tienen una interpretación con algún significado para nosotros.
A estos mundos que se pueden adaptar a un lenguaje particular, $L$, se les denomina comúnmente **$L$-estructuras** (un mundo se puede ajustar a muchos lenguajes, y un mismo lenguaje se puede ajustar a muchos mundos posibles).
Así pues, informalmente, una $L$-estructura $M$ es un conjunto en el que cada símbolo del lenguaje $L$ se puede interpretar como un elemento, propiedad o función real en ese conjunto. De hecho, a la identificación concreta que dice cómo se interpreta cada símbolo de $L$ se le llama **interpretación**. Es esta interpretación la que da sentido a los elementos del lenguaje que, hasta este momento, no eran más que símbolos sin contenido, sin más utilidad que la de poder escribir expresiones correctamente.
!!!Tip
Una intepretación *natural* del ejemplo anterior sería considerar el mundo antiguo formado por romanos y pompeyanos como conjunto de *objetos*, y el significado natural de cada uno de los predicados, constantes y funciones. Pero no es la única interpretación posible. Podríamos considerar, en un alarde de imaginación y libertad, que el conjunto de objetos sobre el que se trabaja son los números naturales, donde ${\bf Marco}$ representa al número $0$, ${\bf Cesar}$ representa al número $1$, el padre de un individuo es el siguiente (es decir, por ejemplo, $f({\bf César})$ representa al número $2$), ser romano es ser par, ser pompeyano es ser múltiplo de 4, etc... Los términos y fórmulas escritas en el lenguaje no cambian, pero su interpretación (significado) en este nuevo mundo son completamente distintas, y habrá fórmulas que se verificarán con esta nueva interpretación que quizás en la natural no se verifiquen (o al revés).
Si queremos usar LPO para razonar acerca de lo que ocurre en el mundo, debemos ser capaces de describir el mundo sin que haya posibilidad de que las fórmulas sean verdaderas en estructuras que no tienen nada que ver con el mundo que estamos modelando. Esta tarea no es nada trivial, y a veces, por mucho que queramos especificar concretamente las propiedades que caracterizan el mundo de interés, podemos encontrar **mundos extraños** que verifican las mismas propiedades pero no son nuestro objeto de interés.
Pero, por lo menos, con el fin de modelar el conocimiento de dominios de forma lógica debemos precisar con claridad cuándo una fórmula es verdadera en una cierta estructura:
Diremos que una fórmula, $\varphi$, de $L$ es **satisfactible** si hay una $L$-estructura, $M$, donde se verifica la fórmula (con el significado estándar de los símbolos lógicos y la interpretación en esa estructura de los símbolos de constantes, predicados y funciones), y en este caso se dice que la estructura es **modelo** de la fórmula: $M\models \varphi$. Esta idea se puede extender a un conjunto de fórmulas, $\Sigma$, que será **satisfactible** en una estructura si lo son todas sus fórmulas: $M\models \Sigma$.
!!!Tip
Por ejemplo, en el mundo de los romanos con la interpretación natural se tiene que la fórmula $\forall x (P(x)\rightarrow R(x))$ se satisface (con la interpretación de los números naturales que hemos dado, también).
Y podemos definir el concepto fundamental que persigue la lógica acerca de cuándo podemos **concluir** una fórmula, $\varphi$, de un conjunto de fórmulas, $\Sigma$: $\Sigma\models \varphi$, y es que será así cuando, en todo mundo posible en el que $\Sigma$ se verifique, necesariamente $\varphi$ se verifica. Es decir:
Si $M$ es una $L$-estructura tal que $M\models \Sigma$, entonces $M\models \varphi$.
Observa que, si $\Sigma=\{\varphi_1,\dots,\varphi_n\}$ es un conjunto finito de fórmulas, entonces esta definición es equivalente a decir que $$M\models \varphi_1\wedge \dots\wedge \varphi_n \rightarrow \varphi$$
se tiene para cualquier $L$-estructura $M$.
!!!Tip
Por ejemplo, tomando como $\Sigma$ el conjunto de sentencias formalizadas anteriormente, podríamos preguntarnos si de ellas se deduce (si es consecuencia lógica) si *Marco era leal a César* ($L({\bf Marco},{\bf Cesar})$), o no.
Al igual que se hace con la Lógica Proposicional, sería interesante ver de qué forma podemos dar métodos (y si son automatizables mejor) para comprobar si una fórmula es consecuencia lógica de un conjunto de fórmulas, métodos que no sean el de comprobar directamente la definición, que precisa de verificar la condición anterior sobre todos los mundos posibles, o estructuras.
Para entender cómo se diferencia ahora este objetivo en Primer Orden del equivalente en Proposicional es importante observar que, en Proposicional, si tenemos un conjunto finito de fórmulas que hacen uso de un conjunto finito de variables proposicionales, entonces el número de mundos posibles es finito, ya que consiste simplemente en todas las posibles combinaciones de valores de verdad de las afirmaciones, por lo que bastaría comprobar en cada uno de ellos si se tiene la condición anterior o no (es, esencialmente, lo que se hace con una tabla de verdad). Sin embargo, en Primer Orden no podemos afirmar lo mismo, los mundos son mucho más ricos y complejos, y aunque estemos trabajando con un conjunto finito de fórmulas que hacen uso de un conjunto finito de símbolos, no podemos asegurar que haya únicamente un número finito de mundos posibles, por lo que este método de comprobación exahustiva ya no es válido y hay que buscar métodos alternativos.
Mucho del trabajo realizado en LPO es ver hasta qué punto se pueden extrapolar y adaptar los métodos que funcionan en LP al caso de LPO. Una opción que sí nos trasladaría a una situación similar sería si pudiéramos asegurar que los mundos posibles son finitos y además tenemos un símbolo de constante para nombrar cada uno de ellos, porque en este caso realmente la LPO se estaría usando como una forma más abreviada de escribir fórmulas proposicionales (tendríamos todas las afirmaciones de lo que se puede decir acerca de los objetos del mundo describiéndolas una a una sobre cada objeto... un conjunto resultante de fórmulas muy grande, posiblemente infinito, pero muy simple). Es obvio que este no es el caso general, y de hecho en general no podemos afirmar que todos los mundos posibles (estructuras) vayan a ser finitas. Sin embargo, podemos usar esta idea para tratar de trabajar con una **versión proposicional** de nuestro lenguaje.
Si tenemos en cuenta que tenemos un conjunto de símbolos de constantes, y que los objetos del mundo solo se pueden referenciar en el lenguaje por medio de los términos, que son aquellas expresiones formadas por las combinaciones correctas de estos símbolos con los símbolos de función, entonces de forma efectiva solo podremos referenciar concretamente aquellos objetos del mundo que se puedan nombrar por medio de los términos que no hacen uso de las variables $x,y,z...$, que no representa objetos concretos, es decir, los **términos cerrados**.
!!!Tip
Por ejemplo, $f({\bf Cesar})$ es un tèrmino cerrado, pero $f(x)$, no.
Ten en cuenta que el conjunto de términos cerrados puede ser infinito (basta que haya un símbolo de función y un símbolo de constante para que las combinaciones expresivas en estos términos explote).
Así pues, si consideramos el conjunto de las posibles fórmulas de $\Sigma$ pero instanciando sus variables libres (si las tienen) con los objetos que pueden conseguirse por medio de términos cerrados (lo más probable es que hubiera que añadir algunos símbolos nuevos de constantes y funciones para las fórmulas existenciales que hubiera en $\Sigma$, siguiendo un proceso de skolemnización), tendríamos un conjunto de fórmulas (mucho más grande) pero escrito en un lenguaje equivalente a uno proposicional y que diría exactamente lo mismo que dicen las fórmulas de $\Sigma$. En cierta forma, es el proceso de descomprimir la información que da $\Sigma$ usando las variables libres de un LPO reescribiendo las fórmulas en un lenguaje que habla solo de objetos concretos. Este proceso tan simple conceptualmente es el que está detrás de la famosa (y temida por los alumnos) **extensión de Herbrand**.
!!!Tip
Por ejemplo, a partir de la fórmula $\forall x\, (P(x)\rightarrow R(x))$ del conjunto $\Sigma$ anterior obtendríamos las siguientes versiones sin variables (que hacen uso de términos cerrados únicamente):
$$P({\bf Marco})\rightarrow R({\bf Marco}),\ P({\bf Cesar})\rightarrow R({\bf Cesar})\\ P(f({\bf Marco}))\rightarrow R(f({\bf Marco})),\ P(f({\bf Cesar}))\rightarrow R(f({\bf Cesar}))\\ \cdots$$
que, esencialmente, son como fórmulas proposicionales que hacen uso de la "nuevas" variables proposicionales $P({\bf Marco})$, $R({\bf Marco})$, $P({\bf Cesar})$, $R({\bf Cesar})$, $P(f({\bf Marco}))$, ...
El conjunto de estas nuevas versiones con términos cerrados de las fórmulas de $\Sigma$ proporciona una especie de versión proposicional de la información que hay en $\Sigma$, y podríamos intentar aplicarles los métodos de razonamiento propios de los lenguajes LP (observa que estas nuevas fórmulas ya no tienen variables ni cuantificadores, que son la principal diferencia sintáctica entre LP y LPO).
No es la única técnica posible, ni siquiera la más sencilla y cómoda, pero sí la más inmediata que permite aplicar técnicas desarrolladas originalmente para LP al caso de los LPO. Estas técnicas, que se comportan de forma decidible en el caso de LP, se encuentran ante una explosión (a menudo infinita) en esta extensión, lo que hace que el caso LPO sea, en general, indecidible. En otras entradas de este curso puedes encontrar otras técnicas que podemos intentar transferir de LP a LPO.