**SVRAI** Agentes Basados en Utilidades Funciones de Utilidad y Procesos de Markov El objetivo de la investigación en **Sistemas Multiagente** (**SMA**) es encontrar métodos que permitan modelar sistemas complejos por medio de agentes autónomos que, aunque operen con conocimiento local y posean sólo habilidades limitadas, sean capaces de realizar los comportamientos globales (complejos) deseados. En este sentido, nuestro objetivo es saber cómo tomar una descripción de lo que debe hacer un *sistema de agentes* y descomponerla en comportamientos de agentes individuales. En su vertiente más ambiciosa, los SMA tienen como objetivo la *ingeniería inversa de fenómenos emergentes*, como los que se dan en las colonias de hormigas, la economía o el sistema inmunitario: a partir de los comportamientos observados en el sistema completo, la idea es diseñar los comportamientos individuales que dan lugar al comportamiento global. Los SMA abordan el problema utilizando herramientas bien establecidas de disciplinas tan, a priori, diversas como la **Teoría de Juegos**, la **Economía** y la **Biología**, y las complementa con ideas y algoritmos procedentes de la **Inteligencia Artificial** (IA), como son los algoritmos de **Planificación**, los métodos de **Razonamiento Automático**, los algoritmos de **Búsqueda** o el **Aprendizaje Automático** (ML). Bajo tal cantidad de influencias tan dispares, no es raro que la historia de los SMA haya llevado al desarrollo de muchos enfoques diferentes, algunos de los cuales acaban siendo incompatibles entre sí, hasta el punto de que a veces no está claro si dos investigadores están estudiando variaciones del mismo problema o problemas completamente diferentes debido a los enfoques tan distintos con los que trabajan. Sin embargo, el modelo que hasta ahora ha ganado más atención, probablemente debido a su flexibilidad y a que tiene unas raíces bien establecidas en la Teoría de Juegos y la Inteligencia Artificial, es el de modelar a los agentes como *maximizadores de utilidad* que ejecutan algún tipo de *Proceso de Decisión de Markov*. Es por ello que, una vez metidos en materia, introducimos este modelo como primera aproximación de modelado en el curso y, como veremos, será un modelo recurrente a lo largo de otros enfoques. Sin embargo, hay que tener en cuenta que, aunque se trata de un modelo muy general, no siempre es la mejor manera de describir el problema, y por ello, se verán otras aproximaciones habituales desde el punto de vista de la IA clásica, como es la planificación tradicional y el uso de modelos bio-inspirados (es decir, procesos inspirados en Biología). Otro modelo popular es el de agentes como máquinas de inferencia lógica. Este modelo es el preferido por quienes trabajan en aplicaciones semánticas o lógicas. Las aproximaciones son tan distintas que a veces nos referiremos a los agentes que pueden deducir hechos basándose en las reglas de la lógica como **agentes deductivos** (porque deducen el mundo a partir de reglas lógicas y bases de conocimiento formalmente expresadas como verdades de esa lógica), y a los agentes que utilizan técnicas de ML para extrapolar conclusiones a partir de las muestras dadas como **agentes inductivos** (porque inducen el mundo como resultado del aprendizaje que obtienen de los datos reales que de él puede extraer). # Función de Utilidad Una suposición simplificadora común es que las preferencias de un agente pueden ser capturadas por una **función de utilidad**, que mapea los estados posibles del mundo en números reales. Es un concepto tomado de la **Teoría de Juegos**, donde se conoce como la *función de utilidad de von Neumann-Morgenstern*. De esta forma, simplificamos por un artificio matemático (y fácilmente computable) la inclinación del agente, cuanto mayor sea el número asignado a un estado, más preferencia debe mostrar el agente por ese estado en particular, y sus acciones irán encaminadas a alcanzar ese estado del mundo. !!!def:Función de Utilidad En concreto, si $S$ es el conjunto de *estados del mundo que el agente puede percibir*, la función de utilidad del agente será de la forma: $$ u : S \rightarrow \mathbb{R} $$ Obsérvese que solo consideramos aquellos estados del mundo que el agente puede percibir, y no lo estados que podríamos reconocer objetivamente en el mundo. Por ejemplo, si un robot sólo tiene un sensor que le proporciona una entrada binaria, por ejemplo, $1$ si hay luz y $0$ si está oscuro, entonces ese robot tiene una función de utilidad definida sólo sobre $2$ estados, independientemente de lo complicado que sea el mundo real, por ejemplo: $$ u(s) = \left\{ \begin{array}{ll} 5 & \text{, si } s=0 \\ 10 & \text{, si } s=1 \end{array} \right. $$ indicando una preferencia del agente por el estado luminoso. En la práctica, los agentes pueden llegar a tener entradas mucho más sofisticadas (por ejemplo, valores compuestos con componentes continuas) y no es factible definir una salida diferente para cada entrada individual. Por ello, la mayoría de los agentes también acaban mapeando sus *entradas brutas* a un conjunto más pequeño (y manejable) de estados del mundo. En general, la creación de esta función de utilidad (y de la manipulación de estados brutos) puede ser un reto, ya que requiere un profundo conocimiento del dominio del problema y, muchas veces, un proceso de ensayo y error para comprobar que las simplificaciones consideradas siguen permitiendo modelar el comportamiento de forma efectiva. Como la función de utilidad de un agente devuelve números reales, podemos definir un **orden de preferencia** para el agente sobre los estados del mundo. Comparando los valores de utilidad de dos estados podemos determinar cuál es el preferido por el agente. Este orden tiene las propiedades de un **orden total**. !!!def:Órdenes Totales En general, una relación de orden, $\geq$, es **total** si verifica las propiedades: * Reflexiva: $u(s) \geq u(s)$. * Transitiva: Si $u(s_1) \geq u(s_2)$ y $u(s_2) \geq u(s_3)$ entonces $u(s_1) \geq u(s_3)$. * Total: $\forall s,s'\in S$, o bien $u(s) \geq u(s')$ o bien $u(s') \geq u(s)$. Podemos utilizar funciones de utilidad para describir muchísimos tipos de comportamientos en agentes, y también son útiles para capturar las diversas transacciones que un agente debe hacer, junto con el valor, o el valor esperado, de sus acciones. Por ejemplo, podemos interpretar que un robot recibe un determinado pago por entregar un paquete, pero también incurre en un coste en términos de energía utilizada, así como en el *coste de oportunidad*, ya que podría haber estado entregando otros paquetes. Si traducimos todos estos pagos y costes en números de utilidad, tendremos opción de estudiar las contrapartidas entre las acciones que el agente puede ejecutar. La ventaja de esta visión es que, una vez definida una función de utilidad para todos los agentes, *lo único* que tienen que hacer es tomar acciones que maximicen su utilidad. Al igual que en la Teoría de Juegos, utilizamos la palabra *egoísta* para referirnos a un agente racional que quiere maximizar su utilidad. Veremos que el uso de agentes egoístas no excluye ni impide la implementación de SMA *cooperativos*. !!!def:Sistemas Multiagente Cooperativos Podemos ver un SMA cooperativo como uno en el que las funciones de utilidad de los agentes se han definido de tal manera que los agentes *parecen* cooperar. Por ejemplo, si un agente recibe una mayor utilidad por ayudar a otros agentes (aunque sea indirectamente), el comportamiento resultante parecerá cooperativo a un observador externo aunque el agente esté actuando de forma egoísta. En resumen, utilizamos las funciones de utilidad como una forma compacta y matemática de representar el comportamiento de un agente. En las implementaciones reales, estas funciones serán a veces probabilísticas, a veces se aprenderán mientras el agente actúa en el mundo, a veces serán incompletas, a veces serán el resultado de alguna inferencia o inducción. Aun así, asumir que esta función existe nos facilita la tarea de diseñar y estudiar más fácilmente un SMA. !!! 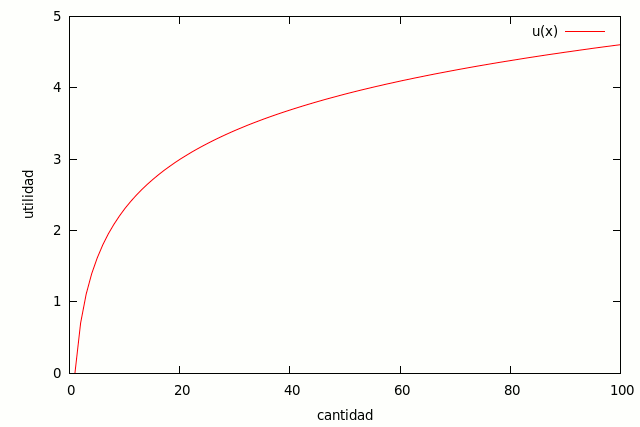Tip:La utilidad no funciona como el dinero Obsérvese que, aunque la utilidad representa las preferencias de un agente, no se equipara necesariamente con el dinero. De hecho, se ha descubierto que la utilidad del dinero se comporta de forma logarítmica. Por ejemplo, supongamos que A tiene 100 millones de euros y B tiene 0 euros en el banco. Ambos contemplan la posibilidad de ganar un millón de euros. Evidentemente, ese millón extra supondrá una diferencia significativa en el estilo de vida de B, mientras que el estilo de vida de A permanecerá prácticamente inalterado, por lo que la utilidad de B para el mismo millón de euros es mucho mayor que la de A. Hay pruebas experimentales que demuestran que la mayoría de la gente tiene este tipo de preferencias condicionales. A grandes rasgos, la utilidad de la gente para cantidades pequeñas de dinero es lineal, pero para cantidades mayores se convierte en logarítmica. Nótese que estamos considerando la *utilidad marginal* del dinero, es decir, es la utilidad para el siguiente millón de euros. Suponemos que tanto A como B tienen la misma utilidad para su primer millón de euros.
 Resultados recientes en economía del comportamiento han demostrado que la verdadera función de utilidad es más complicada de lo que puede captar una función matemática. Un experimento muestra que es menos probable que la gente acepte una apuesta cuando el enunciado de la pregunta es tal que la persona debe devolver algo de dinero, incluso si la apuesta es matemáticamente idéntica a otra que utiliza un enunciado diferente. El experimento en cuestión es el siguiente: ¿qué opción preferirías (a) que te diera 10.000€ y una posibilidad del 50% de ganar otros 10.000€, o (b) que te diera 20.000€ y luego lanzara una moneda, y si saliera cara tendrías que darme 10.000€? Ambas opciones son equivalentes desde el punto de vista funcional, pero la gran mayoría de la gente prefiere la opción (a).
El hecho de que las personas no sean totalmente racionales a la hora de tomar decisiones sobre el dinero se vuelve importante para nosotros cuando empezamos a pensar en construir agentes que compren, vendan o negocien para los humanos. Es razonable suponer que en estos sistemas las personas exigirán agentes que se comporten como personas. De lo contrario, el agente tomaría decisiones que el usuario considera inapropiadas o indeseables. La aparente irracionalidad de las personas también abre la posibilidad de construir agentes que sean mejores negociadores que nosotros. ## Utilidad esperada ![](img/agentes.png align="right")Una vez que tenemos las funciones de utilidad, debemos determinar cómo las utilizarán los agentes. Podemos suponer que cada agente tiene algunos *sensores* que pueden utilizar para determinar el estado del mundo y algunos *efectores/actuadores* que pueden utilizar para realizar acciones sobre el mundo. Ejecutar estas acciones puede conducir al agente a nuevos estados del mundo. Por ejemplo, un agente detecta su ubicación y decide avanzar $1$ metro, tras moverse, el estado del mundo que percibe ha cambiado (presumiblemente). Por supuesto, estos sensores y efectores podrían no funcionar perfectamente: el agente podría no moverse exactamente $1$ metro o sus sensores podrían tener ruido. Supongamos, sin embargo, que el agente conoce la probabilidad de alcanzar el estado $s'$ suponiendo que está en el estado $s$ y realiza la acción $a$. !!!:Función de Transición Estocástica Esta probabilidad viene dada por $T(s,a,s')$ que llamamos **función de transición** ($s \stackrel{a}{\rightarrow} s'$). Como la función de transición devuelve una probabilidad, entonces debe ser cierto que: $$ \begin{equation} \forall a\in A,\; \forall s\in S\; (\sum_{s'\in S}T(s,a,s')=1) \end{equation} $$ Esta es la diferencia principal entre un **Espacio de Estados** (muy común, como hemos visto en los Fundamentos del curso, cuando se trabaja con algunas representaciones para resolución automática de problemas en IA) y la base que nos permitirá manipular SMA con incertidumbre: !!! Tip En un Espacio de Estados, la función de transición devuelve, para cada estado, $s$, y acción, $a$, un estado futuro, $s'=T(s,a)=T_{s,a}$, por lo que se comporta como una función completamente determinista. Sin embargo, cuando hay incertidumbre acerca de la ejecución de la acción, lo que obtenemos es una probabilidad de acabar en cualquiera de los otros posibles estados del mundo: $F_{s,a}(s')=T(s,a,s')$, y por eso al final expresamos la función de transición como una gran función que depende de los tres factores.  !!!def:Utilidad Esperada Bajo la existencia de una función de utilidad, y por medio de esta función de transición, el agente puede calcular la **utilidad esperada** por tomar la acción $a$ en el estado $s$ como: $$ \begin{equation} \label{utilidad-esperada} E[u,s,a] = \sum_{s' \in S} T(s,a,s')u(s') \end{equation} $$ !!! Tip Si se recuerda un poco de estadística básica, esta definición no es distinta de la cualquier esperanza de una variable aleatoria. Un agente puede utilizar la función de utilidad esperada para asignar un valor a las nuevas unidades de información que puede adquirir del entorno, como podría ser la lectura de un sensor adicional o un mensaje de otro agente. Por ejemplo, si una nueva información lleva al agente a determinar que no está realmente en el estado $s$ que creía, sino un estado distinto, $t$. El agente puede comparar la utilidad esperada entre ambos estados, de forma que **valor de la información** recibida podría ser: $$ \begin{equation} \label{valor-informacion} E[u,t,\pi(t)] - E[u,t,\pi(s)] \end{equation} $$ Donde $\pi$ representa la estrategia de toma de acciones que el agente usa para determinar qué hacer (evaluando su creencia del estado del mundo). Así, el valor de esta información es la diferencia entre la utilidad esperada que recibe el agente ahora que sabe que está en $t$ (y actúa en consecuencia) y la utilidad que habría recibido si hubiera supuesto erróneamente que estaba en $s$ y hubiera actuado en consecuencia. La ecuación $\ref{valor-informacion}$ proporciona una forma sencilla y robusta para que los agentes tomen decisiones a un nivel superior sobre qué conocimiento buscar: qué mensajes enviar, qué sensores encender, cuánta deliberación realizar, etc. En concreto, un agente puede utilizar esta información para evaluar *qué pasaría si* y determinar su mejor acción de la misma manera que lo haría una persona. !!!Tip Por ejemplo, supongamos que un médico ha tomado una decisión preliminar sobre el medicamento que debe recetar a un paciente, pero no está seguro de la enfermedad concreta de éste. Puede calcular el valor de la información adquirida al realizar varias pruebas que podrían identificar la enfermedad específica. Si una prueba, independientemente de su resultado, llevara al médico a recetar el mismo medicamento, entonces el valor de la información del resultado de esa prueba es nulo: no conduce a un cambio de acción, por lo que el valor de la ecuación anterior sería $0$. Por otro lado, una prueba que probablemente cambie la acción del médico tendrá un valor de información alto. # Procesos de Decisión de Markov ![](img/Andrei_Markov.jpg align="right" width="15%") Hasta ahora hemos asumido que sólo el agente puede cambiar el estado del mundo. Pero, en la mayoría de los casos, la realidad es que los agentes habitan en un entorno cambiante, ya sea por la acción del agente o por acontecimientos externos (otros agentes, por ejemplo). Al igual que antes, podemos pensar que el agente percibe el estado del mundo y luego realiza una acción que le lleva a un nuevo estado. Podemos hacer una suposición simplificadora adicional, y es que la elección del nuevo estado sólo depende del estado actual que percibe el agente y de su acción. Esta idea se recoge formalmente mediante lo que se conoce como **Proceso de Decisión de Markov** (**MDP**). !!!def:Proceso de Decisión de Markov Un **Proceso de Decisión de Markov** (**MDP**) consta de un estado inicial $s_1$ tomado de un conjunto de estados $S$, una función de transición $T(s,a,s')$ y una función de recompensa $r: S \rightarrow \mathbb{R}$. Al igual que antes, la función de transición $T(s,a,s')$ da la probabilidad de que un agente en el estado $s$ que realiza la acción $a$ acabe en el estado $s'$. Para un mundo puramente **determinista**, fijado el par $(s,a)$, esta función será $0$ para todos los $s'$ excepto uno, para el que será $1$. Es decir, en un mundo determinista la acción de un agente tiene un efecto completamente predecible. En un entorno **no determinista** la acción de un agente podría conducir a un conjunto de estados diferentes, dependiendo del valor de esta función de probabilidad fija. 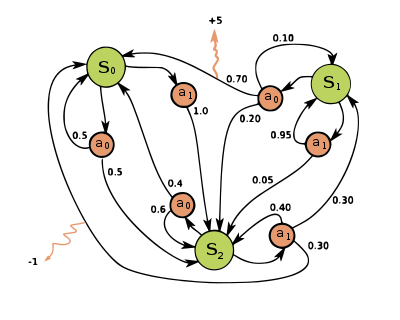![Figura [MDP]: Ejemplo sencillo de MDP](img\sma1-1.png width="75%") !!!Tip La figura [MDP] muestra una representación de un **MDP**, en este caso, con $4$ estados, donde las acciones del agente están limitadas en función del estado. Por ejemplo, en el estado $s_1$ el agente sólo puede realizar las acciones $a_1$ y $a_2$. En este estado, si realiza la acción $a_1$ hay una probabilidad de $0.2$ de que se quede en el mismo estado, y de $0.8$ de que acabe en el estado $s_2$. Además, recibe una recompensa de $1$ sólo cuando llega a $s_3$, momento en el que su única opción es abandonar $s_3$ (por medio de las acciones $a_3$ o $a_4$). !!!:Políticas El comportamiento del agente es capturado por un **política**, que es un mapeo de los estados a las acciones. Usaremos $\pi$ para denotar la política del agente. El objetivo del agente se convierte entonces en encontrar su política óptima, que es la que maximiza su utilidad esperada, como cabría esperar de un agente egoísta. !!!def:Máxima Utilidad Esperada Esta estrategia se conoce como el principio de **máxima utilidad esperada**. La política óptima del agente puede definirse, entonces, como: $$ \begin{equation} \label{maxima-utilidad-esperada} \pi^*(s) = \arg \max_{a \in A} E[u,s,a] \end{equation} $$ Aunque pueda parecer que el problema ya ha sido formalmente expresado, queda decidir acerca de un detalle importante: para maximizar el valor esperado dentro de esa ecuación debemos determinar primero cómo manejar las recompensas futuras. Es decir, ¿es mejor realizar $100$ acciones sin recompensa para llegar a un estado que dé al agente una recompensa de $100$, o es mejor realizar $100$ acciones, cada una de las cuales da al agente una recompensa de $1$? Como es probable que ningún agente viva eternamente, no parece buena idea esperar eternamente por una gran recompensa. Por otro lado, parece razonable renunciar a una pequeña recompensa en los próximos pasos si sabemos que habrá una gran recompensa después. !!!:Recompensas con Descuento Para reflejar esta preferencia doble (buscar recompensas altas, pero no excesivamente tardías), generalmente se utilizan las llamadas **recompensas con descuento**, que permiten reducir suavemente el impacto de las recompensas que están más lejos en el futuro. Una forma de modelarlas es multiplicando las recompensas futuras del agente por un factor de descuento, $\gamma\in (0,1)$ (si $\gamma=0$, el agente se vuelve voraz y busca recompensas inmediatas, y si $\gamma=1$ entonces el agente buscará las mayores recompensas posibles por muy alejadas que estén en el tiempo). Por ejemplo, si un agente que utiliza la política $\pi$, comienza en el estado $s_1$ y visita los estados $s_1, s_2, s_3,\ldots$ entonces su recompensa con descuento vendrá dada por: $$ \begin{equation} \label{descuento} \gamma^0 r(s_1) + \gamma^1 r(s_2) + \gamma^2 r(s_3) + \cdots \end{equation} $$ Aunque intuitivamente es sencilla esta expresión, debemos tener en cuenta que sólo sabemos $s_1$. El resto de los estados, $s_2, s_3,\ldots$ dependen de la función de transición, $T$. Es decir, desde el estado $s_1$ sabemos que la probabilidad de llegar a cualquier otro estado $s'$ por medio de la acción $a$ es $T(s,a,s')$, pero no sabemos a qué estado concreto llegará el agente. Si suponemos que el agente intenta maximizar la utilidad entonces sabemos que va a tomar la acción que maximiza su utilidad esperada. Así, cuando el agente está en el estado $s$ tomará la acción dada por la ecuación $\ref{maxima-utilidad-esperada}$, que cuando se expande utilizando la ecuación $\ref{utilidad-esperada}$ resulta en: !!! $$ \begin{equation} \label{politica-optima} \pi^*(s) = \arg\max_a \sum_{s'} T(s,a,s') u(s') \end{equation} $$ donde $u(s')$ es la utilidad que el agente puede esperar de alcanzar $s'$ y luego seguir obteniendo más recompensas para los estados sucesivos mientras utiliza $\pi^*$. Ahora podemos trabajar hacia atrás y determinar cuál es el valor de $u(s)$. Sabemos que cuando el agente llega a $s$ recibe una recompensa de $r(s)$, pero también sabemos que por estar en $s$ puede realizar su acción basándose en $\pi^*(s)$ y obtendrá una nueva recompensa en el siguiente momento. Por supuesto, esa recompensa será escalada por $\gamma$. !!!def:Ecuación de Bellman ![Richard Ernest Bellman](img\Richard_Ernest_Bellman.jpg align="left") Así, podemos definir la utilidad real que recibe el agente por estar en el estado $s$ como: $$ \begin{equation} \label{ecuacion-Bellman} u(s) = r(s) + \gamma \cdot \max_a \sum_{s'} T(s,a,s')u(s') \end{equation} $$ que se conoce como la **Ecuación de Bellman** y capta el hecho de que la utilidad de un agente no sólo depende de sus recompensas inmediatas, sino también de sus recompensas futuras con descuento. Obsérvese que, una vez que tenemos esta función definida para todos los estados, $s$, también tenemos la verdadera política óptima del agente $\pi^*(s)$, es decir, el agente debe tomar la acción que maximiza su utilidad esperada, como se da en la ecuación $\ref{politica-optima}$. El problema al que nos enfrentamos ahora es cómo calcular $\pi^*(s)$ a partir de la definición del **MDP**. Un enfoque es resolver el conjunto de ecuaciones construidas. Con $n$ estados obtenemos $n$ ecuaciones de Bellman, cada una con una variable diferente. Si el sistema fuera lineal podríamos encontrar los valores para todas estas variables, pero en la práctica la resolución de este conjunto de ecuaciones no es fácil debido al operador $\max$ que aparece en la ecuación de Bellman hace que las ecuaciones no sean lineales. ### Funciones de valor La solución a un MDP se basa normalmente en la estimación de lo que se denominan **funciones de valor óptimas** definidas sobre el conjunto de estados o de acciones. Intuitivamente, una función de valor indica cómo de bueno es para el agente estar en un estado dado o realizar una acción particular en un estado dado. Esta bondad, como hemos visto, depende de las recompensas esperadas en el futuro y, por tanto, de la política que maneje el agente. En el caso general, una política $\pi$ es una función: $$\pi : S \to PD(A)$$ donde $PD(A)$ denota el conjunto de distribuciones de probabilidades sobre las acciones. Este tipo de políticas se denominan **políticas estocásticas**, y especifican de qué manera el agente selecciona las acciones aplicables en cada estado. !!!def: Función de valor-estado para $\pi$ El valor de un estado $s$ bajo una política $\pi$, que denotaremos $V^\pi(s)$, es la utilidad esperada a partir del estado $s$ si se sigue la política $\pi$. Formalmente: $$V^\pi(s)= E_\pi[r_t:\ s_t = s] = E_\pi[\sum_{k=0}^\infty \gamma^k r_{t+k+1}:\ s_t=s]$$ donde $E_\pi$ denota el valor esperado cuando el agente sigue la política $\pi$. A la función $V^\pi$ se le denomina **función de valor-estado para la política $\pi$**. !!!Tip A partir de este punto hemos querido mantener la notación habitual que se usa en los algoritmos de aprendizaje para agentes, que denotan por $V$ la función objetivo que se quiere optimizar, y que se corresponde con la utilidad calculada para cada estado con la que hemos venido trabajando hasta ahora. Solo hay que tener en cuenta que en teoría general de la utilidad, ésta se denota por $u$, mientras que en el caso específico de aprendizaje de políticas por refuerzo pasa a denotarse por $V$. Por ejemplo, una política $\pi$ podría ser, simplemente, elegir en cada uno de los estados $s$, cualquiera de las acciones disponibles (para $s$) con la misma probabilidad. Formalmente: $$\pi(s, a) = \frac{1}{|A(s)|},\ \forall s\in S,\ a\in A(s)$$ donde $A(s)$ es el conjunto de acciones disponibles en el estado $s$, y $|A(s)|$ es su tamaño. Otra política podria ser, en caso de que exista algún orden entre las acciones elegir siempre, en cada estado, la primera acción disponible en dicho estado. Como, en general, el resultado de las acciones es no determinista, la ejecución de una misma política desde un mismo estado puede resultar en una distinta trayectoria y utilidad en cada ejecución, por lo que $V^\pi(s)$ es en sí mismo una variable aleatoria. Así pues, una forma muy primitiva de calcularlo podría consistir en ejecutar $n$ veces la política $\pi$ desde el estado $s$, registrar cada una de las utilidades obtenidas, y luego promediarlas para obtener una estimación de la utilidad esperada. Obviamente, a medida que $n$ crece, esta estimación se acercará al verdadero valor de $V^\pi(s)$. !!!def:Función de valor-acción para $\pi$ Otra función de valor, directamente relacionada a la función de valor-estado $V^\pi$, es la **función de valor-acción**, $Q^\pi$: el valor de la acción $a$ en el estado $s$, que denotaremos $Q^\pi(s, a)$, es la utilidad esperada cuando se comienza en el estado $s$, se toma la acción $a$ y en los pasos sucesivos se sigue la política $\pi$. Formalmente: $$Q^\pi(s, a) = E_\pi[r_t:\ s_t = s,\ a_t = a] = E_\pi[\sum_{k=0}^\infty \gamma^k r_{t+k+1}:\ s_t=s,\ a_t=a]$$ A la función $Q^\pi$ se le denomina **función de valor-acción para la política $\pi$**. !!!Tip Como vemos, y de forma análoga al caso anterior, en el caso de que la utilidad se calcule para cada posible par de estado y acción, $(s,a)$, entonces la utilidad se denota por $Q$, pero no deja de ser la utilidad que se deriva de las recompensas obtenidas por las acciones del agente a más largo plazo. Hasta ahora, hemos definido funciones de valor para políticas arbitrarias, pero nuestro verdadero objetivo es encontrar la política óptima, $\pi^*$, aquella cuya utilidad esperada para todos los estados será mayor o igual al de todas las demás: $$V^{\pi^*}(s)\geq V^\pi(s),\ \forall s\in S,\ \forall \pi\in \Pi$$ $$Q^{\pi^*}(s,a)\geq Q^\pi(s,a),\ \forall s\in S,\ \forall a \in A,\ \forall \pi\in \Pi$$ donde $\Pi$ sería el espacio de políticas posibles. Aunque puede haber más de una política óptima posible, denotaremos a todas ellas por $\pi^*$, y todas comparten la misma función de valor-estado óptima (que denotaremos $V^*$ como una abreviatura para $V^{\pi^*}$). Mientras $V^*$ indica para cada estado cuál es la utilidad esperada máxima que se puede obtener desde ese estado, sobre todas las políticas posibles, es decir cual es la utilidad esperada que se obtiene siguiendo una política óptima, $Q^*$ da la utilidad máxima esperada de tomar la acción $a$ en el estado $s$ y en lo sucesivo seguir una política óptima. ### Métodos de resolución de MDPs Si se dispone de las funciones de valor óptimas $V^*$ o $Q^*$, $\pi^*(s)$ puede ser derivada fácilmente. Aunque hay multitud de técnicas para resolver MDPs, intentaremos ver aquí de forma breve las más representativas: **value-iteration** y **Q-learning**.  #### Value-Iteration Como vimos anteriormente, un enfoque posible para resolver el MDP pasaría por resolver el conjunto de ecuaciones construidas a partir de la Ecuación de Bellman. Con $n$ estados obtenemos $n$ ecuaciones de Bellman, cada una con una variable diferente. Si el sistema fuera lineal podríamos encontrar los valores para todas estas variables, pero en la práctica la resolución de este conjunto de ecuaciones no es fácil debido al operador $\max$ que aparece en la ecuación de Bellman hace que las ecuaciones no sean lineales. Así pues, hay que buscar otro enfoque. Un mecanismo habitual es el de **iteración de valores** (suelen ser mecanismos *recursivos* o que hacen uso de *programación dinámica*, donde la solución óptima de un problema se encuentra calculando primero las soluciones óptimas de ciertos sub-problemas asociados). En este método comenzamos estableciendo los valores de $u(s)$ a valores arbitrarios (por ejemplo, todos a $0$) y luego mejoramos iterativamente estos valores utilizando la **ecuación de actualización de Bellman**: $$ \begin{equation} \label{ecuacion-actualizacion-Bellman} u^{t+1}(s) \leftarrow r(s) + \gamma \max_a \sum_{s'}T(s,a,s')u^t(s') \end{equation} $$ Esta expresión es similar a la ecuación $\ref{ecuacion-Bellman}$, excepto que ahora estamos actualizando los valores de $u$ en el tiempo ($u^t(s)$ refleja la utilidad calculada para $s$ en el instante $t$). Se puede demostrar que este proceso eventualmente, y a menudo rápidamente, convergerá a los valores correctos de $u(s)$. También se sabe que, si el cambio máximo en la utilidad para un paso de tiempo particular es menor que $\epsilon(1-\gamma)/\gamma$, entonces el error es menor que $\epsilon$, lo que puede utilizarse como condición de parada. El algoritmo **value-iteration** es un ejemplo de programación dinámica. En este caso, los subproblemas son las propias variables. Encontrar un valor para una variable ayuda a encontrar valores para otras variables: ~~~~none VALUE-ITERATION(T,r,γ,ε) u = 0 (la función nula) Hacer: │ u = u' │ Para cada s ∈ S hacer: │ u'(s) = r(s) + γ max_a Σ_{s'}T(s,a,s')u(s') │ δ = max_s |u'(s)-u(s)| └ mientras δ > ε(1-γ)/γ Devolver u ~~~~ Por ejemplo, la figura [ValueIteration] muestra cómo cambian los valores de utilidad a medida que se aplica el algoritmo anterior al ejemplo de la figura [MDP]. Las utilidades comienzan en $0$ pero $s_3$ se pone rápidamente en $1$ porque recibe una recompensa de $1$. Esta recompensa se propaga entonces a sus vecinos inmediatos, $s_2$ y $s_4$, en $t=2$ y luego en $t=3$ llega a $s_1$. En $t=4$ el algoritmo se detiene porque el mayor cambio en la utilidad de $t=3$ a $t=4$ fue de $0.13$, que se da en $s_4$, y que es menor que $\epsilon(1-\gamma)/\gamma = 0.15$. ![Figura [ValueIteration]: Ejecución del Algoritmo Value-Iteration](img\sma1-3.png width="70%") !!! Tip El enfoque de la programación dinámica se puede utilizar para resolver una amplia variedad de problemas. Por ejemplo, el motor de búsqueda de Google clasifica los resultados utilizando el **Algoritmo PageRank** en el que el cálculo de la importancia de una página web es proporcional al número de otras páginas que enlazan con ella ponderado por la importancia de esas páginas. Así, la importancia puede calcularse utilizando un mecanismo que es muy similar al algoritmo de iteración de valores. Sin embargo, un problema es que no sabemos cuánto tiempo tardará el algoritmo en converger. Con respecto a la complejidad del algoritmo, podemos observar que si el problema tiene $n$ estados y $m$ es el mayor número de acciones disponibles en cualquier estado, una sola iteración del algoritmo requiere a lo más $O(mn^2)$ operaciones, lo que lo hace competitivo en relación a los métodos de programación lineal y a los métodos que buscan directamente en el espacio de políticas (si consideramos que estos últimos trabajan sobre un espacio que es exponencial en el número de estados). Sin embargo, aunque tiene un desempeño aceptable en problemas involucrando millones de estados, el caracter exhaustivo de las actualizaciones lo hace inapropiado para algunos de los problemas usualmente atacados en IA que involucran espacios de estados mucho más grandes. Por ejemplo, un juego como el backgammon tiene aproximadamente 1020 estados, por lo que una única iteración de este algoritmo llevaría más de un millón de años usando un procesador que pueda actualizar un millón de estados por segundo. #### Q-Learning La principal diferencia de **Q-Learning** con *Value-Iteration* es que la política no se deriva del modelo, sino que es un método de aprendizaje que aproxima la política óptima de forma on-line a partir de la experiencia obtenida por el agente en su interacción con el entorno. Esto le permite enfocarse en el conjunto de estados que se sabe que son más relevantes que otros con respecto al comportamiento óptimo, ya que actualiza aquellos que el agente efectivamente visita en su interacción con el entorno. Q-Learning es, probablemente, uno de los métodos de aprendizaje por refuerzo más conocidos y, como su nombre lo indica, se basa en el aprendizaje de la función $Q^*$. Para entender mejor la regla de actualización utilizada por Q-Learning basta tener en cuenta una propiedad de recurrencia que cumple la función $Q^*$: $$\begin{equation} \label{Q-recurrencia} Q^*(s_t, a_t) = r_{t+1} + \gamma\cdot \max_a Q^*(s_{t+1}, a) \end{equation}$$ donde, como habitualmente, $r_{t+1}$ y $s_{t+1}$ son, respectivamente, la recompensa y el estado alcanzado tras ejecutar la acción $a_t$ en el estado $s_t$. Si quisiéramos usar esta propiedad en una regla de actualización de una tabla $Q$ que aproxime $Q^*$, deberíamos ir actualizando los valores $Q(s_t, a_t)$ de forma que en cada paso de tiempo en que el agente elige una acción $a_t$ en un estado $s_t$, el valor de $Q(s_t, a_t)$ se acerque un ratio $\alpha$ al valor $r_{t+1} + \gamma \max_a Q(s_{t+1}, a)$ y mantenga el ratio complementario $(1 − \alpha)$ del valor previo de $Q(s_t, a_t)$. Más formalmente: $$\begin{equation} Q(s_t, a_t) \leftarrow \alpha \left( r_{t+1} + \gamma \cdot\max_a Q(s_{t+1}, a)\right) + (1 − \alpha)Q(s_t, a_t) \end{equation}$$ !!!def:Reglas de Actualización de $Q$ La ecuación anterior da lugar directamente a la conocida **regla de actualización de los valores de Q** del par $(s_t, a_t)$ utilizada por Q-Learning: $$\begin{equation} \label{Q-actualizacion} Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha \left( r_{t+1} + \gamma\cdot \max_a Q(s_{t+1}, a) − Q(s_t, a_t)\right) \end{equation}$$ Como se puede observar, una de las ventajas de Q-Learning es que permite resolver MDPs con dinámicas incompletas (no requiere conocer la dinámica completas del sistema por la toma de todas las acciones) ya que actualiza sus valores en base a las recompensas que va obteniendo en su interacción con el entorno. El algoritmo **Q-Learning** completo se muestra a continuación: ~~~~none Q-LEARNING Inicializar Tabla Q(s, a) para cada s ∈ S y cada a ∈ A(s) (con 0’s o valores arbitrarios). Repetir: │ Inicializar s. │ Hacer: │ │ Elegir a desde s usando una política derivada de Q. │ │ Ejecutar a, observar estado resultante s′ y recompensa r. │ │ Q(s, a) ← Q(s, a) + α[r + γ max_a′Q(s′, a′) − Q(s, a)] │ │ s ← s′ └ └Hasta que s sea terminal ~~~~ La única restricción que a veces se impone es que si $s$ es un estado terminal, entonces $Q(s,a)=0$ para cualquier acción $a$. El **índice de aprendizaje**, $\alpha$, determina hasta qué punto la información adquirida sobrescribe la información vieja. Un factor de $\alpha=0$ hace que el agente no aprenda (únicamente hace uso del conocimiento inicial), mientras que un factor de $\alpha=1$ hace que el agente considere solo la información más reciente (ignorando el conocimiento previo para explorar posibilidades). En entornos totalmente deterministas, un índice de aprendizaje de $\alpha=1$ es óptimo. Cuando el problema es estocástico, el algoritmo converge cuando $\alpha=\alpha_t \to_{t\to \infty} 0$. Aunque en la práctica a menudo se utiliza un índice de aprendizaje constante, por lo que en un número finito de pasos (a veces determinado por condiciones definidas a priori, como alcanzar un determinado estado final o un número previo de iteraciones) solemos disponer de una buena aproximación. En la línea 5 del algoritmo se hace referencia a la elección de una acción usando una política derivada de Q. Aunque esta política podría limitarse a elegir de forma voraz la acción con valor máximo de Q en ese momento, suele aplicarse un procedimiento que permita un mínimo de exploración de otras acciones alternativas. Un ejemplo de una política muy simple que cumple con este objetivo es la **política $\epsilon$-voraz**, en la que el agente se comporta de forma voraz por defecto pero, con probabilidad $\epsilon$, elige una acción aleatoria de las disponibles. Al ser un algoritmo iterativo, implícitamente supone una condición inicial antes de la primera actualización. Los valores iniciales altos, también conocidos como **condiciones iniciales optimistas**,​ promueven la exploración: independientemente de la acción seleccionada, la regla de actualización provocará que tenga valores menores que la otra alternativa, y por tanto aumentará su probabilidad de elección. La primera recompensa puede ser utilizada entonces para reiniciar las condiciones iniciales.​ Según esta idea, la primera vez que se elige una acción, se fija el valor de la recompensa, lo que permite el aprendizaje inmediato en caso de recompensas deterministas fijas. #### Otras opciones Los MDPs se han convertido en el marco teórico que soporta el cada vez más influyente área de **Aprendizaje por Refuerzo**. Este tipo de aprendizaje se ha enfocado, principalmente, en aproximar 3 de las componentes principales asociadas con un MDP: 1. Las funciones de valor óptimas ($Q^*$ y $V^*$). 2. La política óptima ($\pi^*$). 3. Las dinámicas de un paso del sistema ($T$ y $r$). Entre todas las opciones disponibles para aprender funciones de valor óptimas, Q-Learning es sin duda el método más popular. Sin embargo, para su uso en aplicaciones prácticas tiene ciertas limitaciones debido, principalmente, al hecho de representar la función $Q$ por medio de una tabla de dimensiones $|S|\times |A|$. En los problemas del mundo real, es muy fácil que la representación de un estado se asocie a uno, o más, valores continuos, por lo que $|S|$ es infinito, lo que impide el uso de tablas para almacenar los valores de $Q$. Por ello, es común disponer de variantes en las que $Q$ se aproxima por medio de funciones. Recientemente, se hace uso de redes neuronales para este fin, que toman como entrada un estado y devuelven una estimación de la función $Q$ para cada acción. Cuando usamos redes neuronales profundas (que suele ser necesario para obtener una buena aproximación) nos encontramos con el proceso denominado **Deep Q-Learning**, donde destaca el famoso algoritmo **Deep Q-network** (**DQN**).  DQN fue desarrollado por *Google Deep Mind* y evaluado originalmente en el dominio de los juegos de la Atari 2600. Una de las desventajas de este tipo de enfoques es que las pruebas originales sobre la convergencia a $Q^*$ ya no se cumplen, algo que los autores de la investigación original de DQN reconocieron indicando que usar una red neuronal para representar la función $Q^*$ resultó en un comportamiento bastante inestable. Para poder resolver este problema introdujeron algunas ideas claves para estabilizar el entrenamiento, y que fueron las principales causas del éxito que lograron. Con respecto a la segunda aproximación, aprender directamente la política óptima ($\pi^*$) sin *pasar* previamente por las funciones de valor, tal vez los más populares sean los métodos del gradiente de la política (*policy-gradient methods*) y entre ellos el algoritmo **REINFORCE**, que realiza un ascenso del gradiente que comienza con una estimación inicial del valor de los pesos (parámetros) de la política que maximiza el retorno esperado. Finalmente, en el grupo de métodos que durante el aprendizaje también aprenden las dinámicas de un paso del modelo (**métodos basados en modelo**) podemos encontrar enfoques como **Dyna** y **Prioritizeed Sweeping**. Como suele ser habitual, también ha sido muy común encontrar combinaciones de estos 3 enfoques (basado en funciones de valor, basado en políticas y basado en modelos) dando origen a distintos métodos híbridos que han resultado ser muy efectivos. ## Procesos de decisión de Markov multiagente El modelo **MDP** representa los problemas de un solo agente, no de un SMA. Hay varias formas de transformar un MDP en un MDP multiagente. La forma más fácil es simplemente colocar todos los efectos de los otros agentes en la función de transición. Es decir, asumir que los otros agentes no existen realmente como entidades y son simplemente parte del entorno (cada agente solo tendría conciencia de él mismo como individuo, y el resto forma parte de la dinámica del mundo). Esta técnica puede funcionar para casos sencillos en los que los agentes no cambian su comportamiento, ya que la función de transición en un MDP debe ser fija. Desafortunadamente, los agentes que cambian sus políticas con el tiempo, ya sea por su propio aprendizaje o por las aportaciones de los usuarios, son muy comunes y deseables. Un método mejor es ampliar la definición de MDP para incluir múltiples agentes, cada uno de los cuales puede tomar una acción en cada unidad de tiempo. Así, en lugar de tener una función de transición $T(s,a,s')$ tenemos una función de transición $T(s,\vec{a},s')$, donde $\vec{a}$ es un vector de tamaño igual al número de agentes y donde cada uno de sus elementos es la acción de un agente (se incluye la *no acción* de un agente como posible acción). También tenemos que determinar cómo se va a repartir la recompensa $r(s)$ entre los agentes. Una posibilidad es dividirla por igual entre los agentes. Por desgracia, una división tan simplista puede inducir a error a los agentes al recompensarles por sus malas acciones porque hay otros que lo están haciendo bien. Así que un método mejor es dar a cada agente una recompensa proporcional a su contribución a la recompensa global del sistema. Veremos más adelante cómo se puede hacer esto. ## MDPs Parcialmente Observables En muchas situaciones no es posible que el agente perciba el estado completo del mundo. Además, las observaciones de un agente suelen estar sujetas a ruido. Por ejemplo, un robot sólo tiene sensores limitados y puede que no sea capaz de ver detrás de las paredes o de oír sonidos suaves, y su micrófono puede fallar a veces en la captación de sonidos. En estos casos, nos gustaría poder describir el hecho de que el agente no sabe en qué estado se encuentra, sino que cree que puede estar en un cierto conjunto de estados con cierta probabilidad. Por ejemplo, un robot puede creer que está en una de varias salas de un complejo industrial, cada una con una probabilidad posiblemente distinta (por características del entorno que percibe), pero que definitivamente no está en el exterior. !!!def:Proceso de Decisión de Markov Parcialmente Observable Podemos capturar este problema modelando el **estado de creencia**, $\vec{b}$ (de *believe*), del agente en lugar del estado del mundo. Este estado de creencia es simplemente una distribución de probabilidad sobre el conjunto de estados posibles e indica la creencia del agente de que está en ese estado. Para el caso de cuatro estados, el vector $\vec{b} = \langle \frac{1}{2}, \frac{1}{2}, 0, 0\rangle$ indica que el agente cree que está en $s_1$ o $s_2$, con igual probabilidad, y que no está ni en $s_3$ ni en $s_4$. También necesitamos un **modelo de observación**, $O(s,o)$, que indique al agente la probabilidad de que perciba la observación $o$ cuando esté en el estado $s$. El agente puede entonces utilizar las observaciones que recibe para actualizar su creencia actual, $\vec{b}$. En concreto, si la creencia actual del agente es $\vec{b}$ y realiza la acción $a$, su nuevo vector de creencia $\vec{b}'$ puede determinarse mediante: $$ \begin{equation} \label{actualizacion-creencias} \forall s'\in S \;(\vec{b}'(s') = \alpha \cdot O(s', o) \sum_{s\in S} T(s,a,s')\, \vec{b}(s)) \end{equation} $$ donde $\vec{b}(s)$ es el valor de $\vec{b}$ para $s$, y $\alpha$ es una constante normalizadora que hace que el estado de creencia sume $1$. Cuando juntamos todos estos requisitos tenemos un **Proceso de Decisión de Markov Parcialmente Observable** o **POMDP** que proporciona una forma muy natural de describir los problemas a los que se enfrenta un agente con sensores limitados. Por supuesto, como el agente no conoce el estado, no puede utilizar la iteración de valores para resolver este problema. Por suerte, resulta que podemos utilizar la ecuación $\ref{actualizacion-creencias}$ para definir una nueva función de transición: $$ \tau(\vec{b},a,\vec{b}') = \left\{ \begin{array}{ll} \displaystyle{\sum_{s'\in S}O(s',o) \sum_{s\in S} T(s,a,s')\,\vec{b}(s)} & \text{, si \ref{actualizacion-creencias} es verdad para }\vec{b},a,\vec{b}' \\ 0 & \text{, en otro caso} \end{array} \right. $$ y una nueva función de recompensa: $$ \rho(\vec{b}) = \sum_{s\in S} \vec{b}(s) r(s) $$ Resolver un POMDP en un estado físico equivale a resolver este MDP en el estado de creencia. Desgraciadamente, este MDP puede tener un número infinito de estados ya que las creencias son valores continuos. Por suerte, existen algoritmos para resolver este tipo de MDPs. Estos algoritmos funcionan agrupando las creencias en regiones y asociando acciones a cada región. En general, sin embargo, cuando nos enfrentamos a un problema de POMDP suele ser más fácil utilizar una red de decisión dinámica para representar y resolver el problema. # Planificación en SMA !!! Podemos revisar los problemas de **Planificación** y compararlos con lo que hemos visto en esta unidad. En ellos, también se le proporciona a un agente un conjunto de estados posibles y se le pide una secuencia de acciones que lo lleven hasta un estado deseable del mundo. Sin embargo, en lugar de una función de transición, el agente recibe un conjunto de operadores. Cada operador tiene unos prerrequisitos que especifican cuándo puede utilizarse -en qué estados- y unos efectos que especifican los cambios que el operador provocará en el estado del mundo. El problema de planificación consiste en encontrar una secuencia de operadores que lleven al agente desde el estado inicial hasta el estado objetivo. Podemos ver entonces los problemas de Planificación como casos especiales de MDP, donde sólo el conjunto de estados finales deseados proporcionan recompensa y todas las transiciones tienen una probabilidad de $1$ o $0$. Las transiciones se generan aplicando los operadores al estado actual. Describiendo el problema mediante operadores conseguimos una definición mucho más compacta del problema que enumerando todos los estados y las probabilidades de transición como se hace en un MDP. Aun así, nuestro objetivo es resolver el problema, no definirlo con el menor número de elementos posible. Sin embargo, una descripción más detallada de los estados proporciona una ventaja sobre el simple listado de estados utilizado en MDP, ya que proporciona información adicional sobre la composición del estado. Por ejemplo, si queremos llegar a un estado que tenga las propiedades de $P_1$ y $P_2$, podemos utilizar este conocimiento para conseguir que el estado del mundo verifique $P_1$ y, una vez hecho esto, conseguir que verifique $P_2$ sin perder la propiedad $P_1$. Este tipo de información es opaca en una descripción MDP que simplemente describe un estado $P_1\wedge P_2$ como $s_{11}$ y un estado $P_1\wedge \neg P_2$ como $s_{23}$. Los operadores y sus correspondientes descripciones de estado proporcionan así al agente más conocimiento sobre el dominio del problema. Existen muchos algoritmos que resuelven el problema básico de Planificación y variaciones del mismo, incluyendo casos en los que existe la posibilidad de que los operadores no tengan el efecto deseado (lo que lo hace aún más parecido a un MDP), casos en los que el agente debe empezar a tomar acciones antes de que el plan pueda ser terminado (ejecución en tiempo real), y casos en los que existe incertidumbre sobre en qué estado se encuentra el agente (como POMDP). La mayoría de los algoritmos de planificación modernos utilizan una representación en forma de grafo del problema (muchas veces con elementos de alguna lógica), y cada nodo del grafo puede ser interpretado como un estado. Es decir, acaban convirtiendo el problema en un problema tipo MDP y lo resuelven. ## Planificación jerárquica Una técnica muy exitosa para manejar la complejidad es dividir recursivamente un problema en otros más pequeños hasta que encontremos problemas lo suficientemente pequeños como para que puedan ser resueltos en un tiempo razonable. Esta idea general se conoce como el enfoque **divide y vencerás** en IA (y en la resolución de problemas general). Dentro de la planificación, se puede aplicar mediante el desarrollo de planes cuyos operadores primitivos son otros planes. Por ejemplo, para lograr el objetivo de unas vacaciones en la playa, primero hay que organizar el transporte, el alojamiento y la comida. Cada una de ellas puede descomponerse en acciones más pequeñas, y puede haber diferentes formas de realizar esta descomposición. Dentro del modelo de planificación, esto equivale a construir operadores virtuales que son problemas de planificación en sí mismos, en lugar de acciones atómicas. El problema consiste entonces en decidir qué operadores virtuales construir. De hecho, el problema es muy similar al de decidir qué funciones o clases escribir cuando se implementa un proyecto de software de cierta envergadura. Desde el punto de vista del modelo MDP, podemos imaginar la construcción de una jerarquía de políticas, cada una partiendo de los estados que se ajustan a una descripción particular (por ejemplo, los estados que verifican $P_1$) y devolviendo otros tipos de estados (por ejemplo, los estados que verifican $P_2$). A continuación, podemos definir nuevos problemas MDP que utilicen conjuntos de estados como estados atómicos y las nuevas políticas como funciones de transición, de forma similar a como construimos los POMDP. Estas técnicas se estudian en lo que se conoce como **Aprendizaje Jerárquico**. La planificación y el aprendizaje jerárquico suelen estudiarse como formas de facilitar los problemas de planificación y aprendizaje, es decir, como formas de desarrollar algoritmos que encuentren soluciones más rápidamente. Sin embargo, una vez desarrolladas, estas jerarquías aportan ventajas adicionales en un sistema multiagente. En concreto, pueden utilizarse para permitir la coordinación entre agentes. Al intercambiar los nombres de los planes de alto nivel (o políticas), los agentes tienen una idea general de lo que hacen los demás sin necesidad de intercambiar instrucciones detalladas de lo que hacen en cada paso. Por ejemplo, con dos robots que mueven cajas en una habitación, uno puede decirle al otro que está moviendo una caja de la esquina sur a la esquina este, y el otro agente sabe entonces que si se queda en la parte noroeste de la habitación no necesita preocuparse por la ubicación exacta de su compañero: los robots se mantienen fuera del camino del otro sin necesidad de una coordinación detallada. Esta técnica de uso de jerarquías de objetivos/planes/políticas para la coordinación multiagente ha tenido mucho éxito y la examinaremos más adelante. # Resumen !!! Tip La visión de un agente autónomo como un agente maximizador de la utilidad que habita en un mundo modelado con MDP, o una variación del mismo, es muy popular debido a su flexibilidad, aplicabilidad a dominios dispares, y facilidad de análisis formal con herramientas matemáticas o computacionales. Por ello, se adopta muchas veces este enfoque como base para formular diversos problemas de modelado de sistemas complejos. Sin embargo, hay que tener en cuenta que MDP es una herramienta para describir el problema al que se enfrenta un agente. En la práctica, es raro que una solución práctica a un problema del mundo real se implemente también como un algoritmo para resolver el MDP en bruto. Lo más habitual es encontrar algoritmos que utilizan un método mucho más compacto, y por tanto práctico, para representar el problema. Desgraciadamente, estas representaciones tienden a ser muy específicas del dominio y es complicado trasladarlas de un dominio a otro. Por ello, ha de tenerse en cuenta que es común que, al estudiar soluciones genéricas, no sean eficientes en muchos de problemas concretos, ya que ofrecen una primera aproximación que ha de ser depurada y adaptada a las características concretas del problema. # Ejercicios 1. Implementar de forma genérica los algoritmos **Value-Iteration** y **Q-Learning** para trabajar sobre MDPs definidos a partir de redes aleatorias. Genera experimentos que te permitan determinar cuánto tarda en converger a medida que aumenta el número de estados (ten cuidado de asegurarte de que el grafo de estados sea conexo), incluyendo un pequeño análisis de la importancia de los posibles parámetros de cada algoritmo. 2. Disponemos de un mundo en el que hay unos agentes que han de encontrar el camino más rápido para llegar a unas bases de seguridad (marcadas en verde) evitando las zonas peligrosas del mapa (marcadas en rojo). Aplicar un algoritmo **Value-Iteration**/**Q-Learning** para diseñar la política óptima que lleva a cada agente a su zona de seguridad más próxima evitando el peligro (si no añadimos mecanismos de rutas adicionales, ten cuidado de hacer que las dimensiones del mundo no sean muy grandes). 3. Marvin es un robot que habita en una cuadrícula de $3\times 3$ y sólo puede moverse hacia el Norte, Sur, Este y Oeste. Las ruedas de Marvin giran a veces, de modo que en cada acción hay una probabilidad de $0,2$ de que Marvin permanezca inmóvil. Marvin recibe una recompensa de 1 cada vez que visita la casilla central: 1. Dibuja un MDP que describa el problema de Marvin. 2. ¿Cuál es la política óptima? 4. Tenemos una mesa con tres bloques encima marcados con las letras A, B y C. Supongamos que el estado del mundo está completamente definido por la posición de los bloques entre sí, donde un bloque sólo puede estar en la mesa o encima de otro bloque. Como máximo, solo se pueden montar pilas de tamaño 2. Además, se dan los siguientes operadores: * *mover-a-la-mesa*$(b)$: Requiere que $b$ no tenga ningún otro bloque encima. El resultado es que el bloque $b$ está ahora en la mesa. * *mover-sobre-bloque*$(b_1, b_2)$: Requiere que $b_1$ y $b_2$ no tengan ningún otro bloque encima. El resultado es que el bloque $b_1$ queda encima del bloque $b_2$. Dibuja un MDP para este dominio asumiendo que los operadores no tienen incertidumbre ni ruido. 5. Implementar un programa de NetLogo donde los patches se establecen al azar a un color entre: $negro$, $rojo$ y $verde$. Hay un agente en este mundo que sólo puede moverse hacia el Norte, Sur, Este y Oeste por un patch a la vez. Cada vez que cae en un patch recibe una recompensa determinada por el color del parche: $negro=0$, $rojo=-1$, y $verde=1$.
El movimiento del agente es ruidoso, por lo que cuando decide moverse hacia el Norte termina en el patch Norte deseado con una probabilidad de $0.5$, en el patch Noreste de su ubicación actual (un patch diagonalmente adyacente) con una probabilidad de $0.25$, y en el patch Noroeste de su ubicación actual con una probabilidad de $0.25$.
Aplica el algoritmo **Value-Iteration**/**Q-Learning** para este dominio y encuentra la política óptima.