**SVRAI**
Metaheurísticas
Primera Parte
En Inteligencia Artificial (IA) se emplea el calificativo **heurístico**, en un sentido muy genérico, para aplicarlo a todos aquellos aspectos que tienen que ver con el empleo de conocimiento en la realización dinámica de tareas.
Se habla de heurística para referirse a *una técnica, método o procedimiento inteligente de realizar una tarea que no es producto de un riguroso análisis formal, sino de conocimiento experto sobre la tarea*.
En especial, se usa el término heurístico para referirse a un procedimiento que trata de aportar soluciones a un problema con un buen rendimiento, en lo referente a la calidad de las soluciones y a los recursos empleados.
En la resolución de problemas específicos han surgido procedimientos heurísticos exitosos, de los que se ha tratado de extraer lo que es esencial en su éxito para aplicarlo a otros problemas o en contextos más extensos. Como ha ocurrido claramente en diversos campos de la IA, en especial con los sistemas expertos, esta línea de investigación ha contribuido al desarrollo científico del campo de las heurísticas y a extender la aplicación de sus resultados. De esta forma, se han obtenido tanto técnicas y recursos computacionales específicos, como estrategias de diseño generales para procedimientos heurísticos de resolución de problemas. Estas estrategias generales para construir algoritmos, que quedan por encima de las heurísticas y van algo más allá, se denominan **metaheurísticas**.
Las metaheurísticas pueden usarse como un sistema para facilitar su uso genérico a la vez que mejorar el rendimiento. Aquí describiremos los fundamentos que permiten establecer, partiendo de la noción de heurística, el concepto de metaheurística y mostraremos una primera clasificación de las metaheurísticas a partir de los diferentes tipos de procedimientos heurísticos para los que establecen pautas de diseño.
# Concepto de Metaheurística
La idea más genérica del término *heurístico* está relacionada con la tarea de resolver inteligentemente problemas reales usando el conocimiento disponible. El término heurística proviene de una palabra griega con un significado relacionado con el concepto de *encontrar*, y se vincula a la supuesta exclamación *eureka!* dada por Arquímedes al descubrir su famoso principio.
La concepción más común en IA es interpretar que *heurístico* es el calificativo apropiado para los procedimientos que, empleando conocimiento acerca de un problema y de las técnicas aplicables, tratan de aportar soluciones (o acercarse a ellas) usando una cantidad de recursos (generalmente tiempo) razonable. En un problema de optimización, aparte de las condiciones que deben cumplir las soluciones factibles del problema, se busca aquella que es óptima según algún criterio de comparación entre ellas. En Investigación Operativa, el término *heurístico* se aplica a un procedimiento de resolución de problemas de optimización con una concepción diferente, ya que se califica de heurístico a un procedimiento para el que se tiene un alto grado de confianza en que encuentren soluciones de alta calidad con un coste computacional razonable, aunque no se garantice su optimalidad o su factibilidad, e incluso, en algunos casos, no se llegue a establecer lo cerca que se está de dicha situación deseable.
En este sentido, se usa el calificativo *heurístico* en contraposición a *exacto*, que se aplica a los procedimientos a los que se les exige que la solución aportada sea óptima o factible. Una solución heurística de un problema es la proporcionada por un método heurístico, es decir, aquella solución sobre la que se tiene cierta confianza de que es factible y óptima, o de que alcanza un alto grado de optimalidad y/o factibilidad. También es usual aplicar el término *heurística* cuando, utilizando el conocimiento que se tiene del problema, se realizan modificaciones en su procedimiento de solución que, aunque no afectan a la complejidad del mismo, mejoran el rendimiento en su comportamiento práctico.
Unas heurísticas para resolver un problema de optimización pueden ser más generales o específicas que otras. Los métodos heurísticos específicos deben ser diseñados a propósito para cada problema, utilizando toda la información disponible y el análisis teórico del modelo. Los procedimientos específicos bien diseñados suelen tener un rendimiento significativamente más alto que las heurísticas generales. Estas heurísticas más generales, por el contrario, presentan otro tipo de ventajas, como la sencillez, adaptabilidad y robustez de los procedimientos. Sin embargo, las heurísticas generales emanadas de las metaheurísticas pueden mejorar su rendimiento utilizando recursos computacionales y estrategias inteligentes.
El término **metaheurística** se obtiene de anteponer a heurística el sufijo *meta* que significa "más allá" o "a un nivel superior". Los conceptos actuales de lo que es una metaheurística están basados en las diferentes interpretaciones de lo que es una forma inteligente de resolver un problema. Las metaheurísticas son estrategias inteligentes para diseñar o mejorar procedimientos heurísticos muy generales con un alto rendimiento.
El término metaheurística apareció por primera vez en el artículo seminal sobre búsqueda tabú de Fred Glover en 1986. A partir de entonces han surgido multitud de propuestas de pautas para diseñar buenos procedimientos para resolver ciertos problemas que, al ampliar su campo de aplicación, han adoptado la denominación de metaheurísticas.
La relevancia de las metaheurísticas se refleja en el elevado número de publicaciones sobre este campo desde entonces.
# Tipos de metaheurísticas
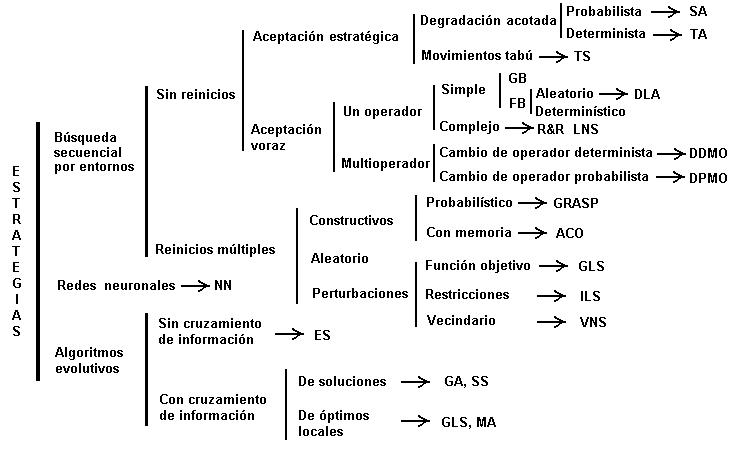
Las metaheurísticas son estrategias para diseñar procedimientos heurísticos. Por tanto, los tipos de metaheurísticas se establecen, en primer lugar, en función del tipo de procedimientos a los que se refiere. Algunos de los tipos fundamentales son:
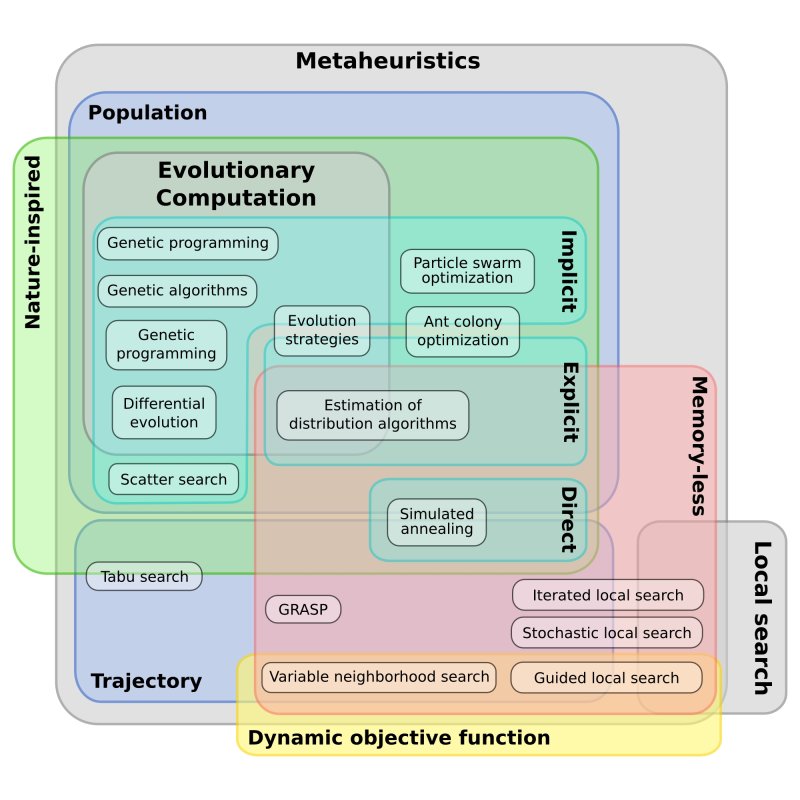
- Las **metaheurísticas de relajación** se refieren a procedimientos de resolución de problemas que utilizan relajaciones del modelo original (es decir, modificaciones del modelo que hacen al problema más fácil de resolver), cuya solución facilita la solución del problema original (más complicado).
- Las **metaheurísticas constructivas** se orientan a los procedimientos que tratan de obtener una solución a partir del análisis y selección paulatina de las componentes que la forman.
- Las **metaheurísticas de búsqueda** guían los procedimientos que usan transformaciones o movimientos para recorrer el espacio de soluciones alternativas y explotar las estructuras de entornos asociadas.
- Las **metaheurísticas evolutivas** están enfocadas a los procedimientos basados en conjuntos de soluciones que evolucionan sobre el espacio de soluciones para acercarse a la solución deseada.
Algunas metaheurísticas surgen combinando metaheurísticas de distinto tipo, como la metaheurística **GRASP** (**Greedy Randomized Adaptive Search Procedure**), que combina una fase constructiva con una fase de búsqueda de mejora. Otras metaheurísticas se centran en el uso de algún tipo de recurso computacional o formal especial como las redes neuronales, los sistemas de hormigas o la programación por restricciones y no se incluyen claramente en ninguno de los cuatro tipos anteriores.
Por otro lado, de una u otra forma, todas las metaheurísticas se pueden concebir como estrategias aplicadas a procesos de búsqueda, donde todas las situaciones intermedias en el proceso de resolución del problema se interpretan como elementos de un espacio de búsqueda, que se van modificando a medida que se aplican las distintas operaciones diseñadas para llegar a la resolución definitiva. Por ello, y porque los procesos de búsqueda heurística constituyen el paradigma central de las metaheurísticas, es frecuente interpretar que el término metaheurística es aplicable esencialmente a los procedimientos de búsqueda sobre un espacio de soluciones alternativas.
En las siguientes subsecciones vamos a profundizar un poco la explicación de las metaheurísticas anteriores:
## Metaheurísticas de Relajación
Una cuestión relevante al abordar un problema real es la obtención de un modelo que permita emplear una técnica de resolución apropiada. Si con este modelo el problema resulta difícil de resolver se acude a modelos modificados en los que es más sencillo encontrar buenas soluciones o en los que los procedimientos son más eficientes. Una relajación de un problema es un modelo simplificado obtenido al eliminar, debilitar, o modificar restricciones (u objetivos) del problema real. En cualquier formulación siempre existe algún grado de simplificación, lo que puede afectar en mayor o menor medida al ajuste a la realidad de los procedimientos de resolución y de las soluciones del problema propuestas. Los modelos muy ajustados a la realidad suelen ser muy difíciles de resolver, y sus soluciones difíciles de implementar exactamente, por lo que se acude a modelos relajados.
Muchas heurísticas de relajación modifican elementos del problema para proponer la solución de estas modificaciones como solución heurística del problema original. Las buenas relajaciones son las que simplifican el problema y hacen más eficientes los procedimientos de solución, pero cuya resolución proporciona muy buenas soluciones del problema original. Por ejemplo, para un problema de programación lineal entera, su **relajación lineal** consiste en ignorar la restricción de que las variables sean enteras. Se utiliza frecuentemente para aplicar procedimientos eficientes de programación lineal, como el método del Simplex, a dicha relajación y proponer una solución entera muy próxima a la solución del problema relajado.
Entre las metaheurísticas de relajación se encuentran los métodos de **relajación lagrangiana** o **de restricciones subordinadas**. Otras metaheurísticas de relajación alteran las restricciones o los objetivos del problema para usar su solución en la conducción de la búsqueda de la solución del problema original. Esta modificación puede estar encaminada a relajar las restricciones a las que debe estar sometida la solución, permitiendo que el recorrido bordee la región factible para acercarse al óptimo global incluso desde la región no factible. Otras estrategias modifican la función objetivo para obtener, de forma más rápida, valoraciones aproximadas (por exceso o por defecto) de la calidad de la solución que orientan la búsqueda, al menos en los estados iniciales. Es frecuente encontrar problemas en los que evaluar la función objetivo puede significar resolver otro problema de gran dificultad, realizar un proceso de simulación o realizar algún tipo de inversión o consumo de recursos. Para estos problemas es muy útil encontrar funciones sencillas de calcular que den una idea aproximada de la calidad de las soluciones sin necesidad de una evaluación ajustada de la función objetivo. Por ejemplo, en juegos complicados, como el ajedrez, encontrar una función que evalúe correctamente la bondad de una posición determinada (que puede depender de los movimientos futuros que esa posición permite) puede llegar a ser excesivamente complicado y costoso, por lo que muchas veces se usa una función de evaluación que hace un simple cálculo acerca de dónde está cada pieza en la posición considerada... no es perfecta, pero permite hacer muchas más evaluaciones por segundo y explorar más los posibles futuros para encontrar un buen movimiento (quizás no el mejor) en una cantidad de tiempo razonable.
## Metaheurísticas Constructivas
Las heurísticas constructivas aportan soluciones del problema por medio de un procedimiento que incorpora iterativamente elementos a una estructura, inicialmente vacía, que representa a la solución. Las metaheurísticas constructivas establecen estrategias para seleccionar las componentes con las que se construye una buena solución del problema. Entre las metaheurísticas primitivas en este contexto se encuentra la popular **estrategia voraz** o **greedy**, que implica la elección que da mejores resultados inmediatos, sin tener en cuenta una perspectiva más amplia. Dentro de este tipo de metaheurística, destaca la aportación de la metaheurística **GRASP** que, en la primera de sus dos fases, incorpora a la estrategia greedy pasos aleatorios con criterios adaptativos para la selección de los elementos a incluir en la solución.
Por ejemplo, se usa una metaheurística constructiva de este tipo cuando se construye un camino mínimo en un mapa usando la opción de cambio más cercana al objetivo... no asegura un camino mínimo final, pero al menos reduce la complejidad de la decisión en cada paso confiando en que los puntos más cercanos nos llevarán más rápido al objetivo final.
## Metaheurísticas de búsqueda
El tipo de metaheurística más importante es el de las metaheurísticas de búsqueda, que establecen estrategias para recorrer el espacio de soluciones del problema transformando de forma iterativa soluciones de partida.
La concepción primaria de heurística más frecuente era la de alguna regla inteligente para mejorar la solución de un problema que se aplicaba iterativamente mientras fuera posible obtener nuevas mejoras. Tales procesos se conocen como **búsquedas monótonas** (descendentes o ascendentes), **algoritmos escaladores** (hill-climbing) o **búsquedas locales**.
Esta última denominación obedece a que la mejora se obtiene en base al análisis de soluciones similares a la que realiza la búsqueda; denominadas *soluciones vecinas*. Estrictamente hablando, una búsqueda local es la que basa su estrategia en el estudio de soluciones del vecindario o entorno de la solución que realiza el recorrido. Las metaheurísticas de búsqueda local son las estrategias o pautas generales para diseñar métodos de búsqueda local, como la estrategia voraz o greedy. Esta metaheurística establece como pauta, una vez consideradas cuales son las soluciones que intervienen en el análisis local, elegir iterativamente la mejor de tales soluciones mientras exista alguna mejora posible.
Sin embargo, se suele asumir que las búsquedas locales sólo modifican la solución que realiza el recorrido mediante una mejora en su propio entorno. El principal inconveniente de estas búsquedas locales es que se quedan fácilmente atrapadas en un óptimo local, una solución que no puede ser mejorada por medio de un análisis local. Por ello, el propósito fundamental de las primeras metaheurísticas era extender una búsqueda local para continuarla más allá de los óptimos locales, denominándose **Búsqueda Global**.
Las metaheurísticas de búsqueda global incorporan pautas para tres formas básicas de escapar de los óptimos locales de baja calidad: volver a iniciar la búsqueda desde otra solución de arranque, modificar la estructura de entornos que se está aplicando, y permitir movimientos o transformaciones de la solución de búsqueda que no sean de mejora. Surgen así, respectivamente, las metaheurísticas de **arranque múltiple**, de **entorno variable** y de **búsqueda no monótona**. Estos últimos controlan los posibles movimientos de empeoramiento de la solución mediante criterios de aceptación estocásticos o utilizando la memoria del proceso de búsqueda.
Las metaheurísticas de búsqueda estocásticas establecen pautas para regular la probabilidad de aceptar transformaciones que no mejoren la solución. El **Templado Simulado** es el exponente más importante de este tipo de metaheurísticas donde la probabilidad de aceptación es una función exponencial del empeoramiento producido. Las metaheurísticas de búsqueda con memoria utilizan información sobre el recorrido realizado para evitar que la búsqueda se concentre en una misma zona del espacio. Fundamentalmente se trata de la **Búsqueda Tabú**, cuya propuesta original prohíbe temporalmente soluciones muy parecidas a las últimas soluciones del recorrido.
## Metaheurísticas evolutivas
Las metaheurísticas evolutivas establecen estrategias para conducir la evolución en el espacio de búsqueda de conjuntos de soluciones (usualmente llamados poblaciones en este contexto) con la intención de acercarse a la solución óptima con sus elementos. El aspecto fundamental de las heurísticas evolutivas consiste en la interacción entre los miembros de la población, frente a las de búsqueda que se guían por la información de soluciones individuales.
Las diferentes metaheurísticas evolutivas se distinguen por la forma en que combinan la información proporcionada por los elementos de la población para hacerla evolucionar mediante la obtención de nuevas soluciones. Los **algoritmos genéticos** y **meméticos**, y los de **estimación de distribuciones** emplean fundamentalmente procedimientos aleatorios, mientras que las metaheurísticas de **búsqueda dispersa** o de **re-encadenamiento de caminos** (**Path Relinking**) emplean procedimientos sistemáticos.
## Otros tipos de metaheurísticas
Otras metaheurísticas que aparecen en varias clasificaciones corresponden a tipos intermedios entre los anteriores. Entre ellas destacan las **metaheurísticas de descomposición** (entre las de relajación y las constructivas) y las de **memoria a largo plazo** (entre las de arranque múltiple y la tabú).
# Propiedades deseables
Son propiedades deseables todas aquellas que favorezcan el interés práctico y teórico de las metaheurísticas. Indicarán direcciones a las que dirigir los esfuerzos para contribuir al desarrollo científico e ingenieril, pero no será posible mejorar todas las propiedades a la vez, dado que algunas son parcialmente contrapuestas. Una relación de tales propiedades debe incluir las siguientes:
- **Simple**. La metaheurística debe estar basada en un principio sencillo y claro, fácil de comprender.
- **Precisa**. Los pasos y fases de la metaheurística deben estar formulados en términos concretos.
- **Coherente**. Los elementos de la metaheurística deben deducirse naturalmente de sus principios.
- **Efectiva**. Los algoritmos derivados de la metaheurística deben proporcionar soluciones de muy alta calidad; óptimas o muy cercanas a las óptimas.
- **Eficaz**. La probabilidad de alcanzar soluciones óptimas de casos realistas con la metaheurística debe ser alta.
- **Eficiente**. La metaheurística debe realizar un buen aprovechamiento de recursos computacionales; tiempo de ejecución y espacio de memoria.
- **General**. La metaheurística debe ser utilizable con buen rendimiento en una amplia variedad de problemas.
- **Adaptable**. La metaheurística debe ser capaz de adaptarse a diferentes contextos de aplicación o modificaciones importantes del modelo.
- **Robusta**. El comportamiento de la metaheurística debe ser poco sensible a pequeñas alteraciones del modelo o contexto de aplicación.
- **Interactiva**. La metaheurística debe permitir que el usuario pueda aplicar sus conocimientos del problema para mejorar el rendimiento del procedimiento.
- **Múltiple**. La metaheurística debe suministrar diferentes soluciones alternativas de alta calidad entre las que el usuario pueda elegir.
- **Autónoma**. La metaheurística debe permitir un funcionamiento autónomo, libre de parámetros, o que se puedan establecer automáticamente.
Varias de estas propiedades están muy relacionadas y apuntan en la misma dirección, como la simplicidad, la precisión y la coherencia. Otras pueden ser valoradas en mayor profundidad cuando se trabaja con metaheurísticas concretas y se ponen a prueba.
Para la resolución práctica de una proporción cada vez mayor de problemas de interés no resulta apropiado utilizar procedimientos diseñados a propósito para cada modelo y dependientes de su estructura particular. Ante la necesidad de utilizar algoritmos heurísticos para dar soluciones, las metaheurísticas proporcionan pautas y estrategias generales de diseño para obtener heurísticas con un alto rendimiento. Las metaheurísticas proporcionan métodos para escaparse de los óptimos locales de mala calidad por lo que, dado que el valor de tales óptimos locales frecuentemente difiere considerablemente del valor del óptimo global, el impacto práctico de las metaheurísticas ha sido inmenso.
Se observan diversas tendencias en las investigaciones sobre técnicas metaheurísticas. Unas tratan de mantener la pureza de los métodos y comprobar su efectividad en nuevos problemas, sin incorporar herramientas de otras metaheurísticas. Otras investigaciones, desde una perspectiva más ingenieril, tratan de aprovechar los recursos proporcionados por cada una de ellas. Para estas últimas, la única cuestión relevante es conocer si el beneficio en el rendimiento, proporcionado por la inclusión de tales herramientas, compensa al esfuerzo de su implementación y al incremento de la complejidad de los códigos resultantes (y su mantenimiento futuro).
El campo de investigación sobre metaheurísticas ofrece más oportunidades para aplicar la intuición que la deducción. En contraste con el éxito práctico de muchas metaheurísticas, el estudio teórico está más retrasado. Frecuentemente se obtienen buenas nuevas heurísticas, con algo de inventiva y gran esfuerzo en el ajuste de numerosos parámetros, pero las razones de por qué funcionan tan bien permanecen desconocidas. La situación es incluso peor para los híbridos, donde las aportaciones de las metaheurísticas implicadas y el beneficio de la interacción raramente son objetos de un estudio experimental bien diseñado.
Algunas propuestas encaminadas a una mejor comprensión de estos aspectos son el estudio de la influencia de la topografía de los óptimos locales y de las trayectorias seguidas por los procesos de búsqueda heurística. El análisis de la evolución de las distancias al óptimo frecuentemente se centran exclusivamente en la desviación del objetivo alcanzado frente al mejor posible. Se puede obtener información más útil si se consideran distancias entre las propias soluciones y no sólo su valor. Los intentos por organizar este campo son numerosos, pero los conceptos principales son raramente definidos con precisión y hay todavía muy pocos teoremas significativos. Ninguna estructura ha conseguido una aceptación general. Más bien, cada grupo de investigación inspirador de una metaheurística tiene su propio punto de vista y habilidad para explicar muchas heurísticas en su propio vocabulario así como para absorber ideas de todo el campo (generalmente bajo la forma de híbridos).
# Metaheurísticas de Búsqueda y Optimización
Como hemos visto en apartados anteriores, las **metaheurísticas de búsqueda** proporcionan estrategias para resolver un problema realizando una búsqueda sobre un espacio cuyos elementos representan las soluciones candidatas alternativas, y que se denomina **Espacio de Soluciones** posibles del problema o **Espacio de Estados**. La representación de las soluciones se realiza a través de una codificación que debe incluir toda la información necesaria para su identificación y evaluación, un problema íntimamente relacionado con la Representación del Conocimiento.
Una **búsqueda** sobre un espacio consiste en generar una sucesión de puntos del espacio en el que cada punto se obtiene del anterior por medio de una serie de transformaciones o movimientos.
Un procedimiento de búsqueda para resolver un **problema de optimización** realiza recorridos sobre el espacio de posibles soluciones y selecciona la mejor solución encontrada en el recorrido. El objetivo de las metaheurísticas de búsqueda es proporcionar pautas para obtener recorridos que proporcionen soluciones de alta calidad atendiendo también a una eficiencia adecuada.
La descripción general de un proceso de resolución de un problema suele seguir una serie de pasos comunes: partiendo de una situación inicial, aplicar iterativamente una operación para modificar la situación actual, hasta que se alcance la situación buscada. En este sentido, un proceso de búsqueda basado en transformaciones o movimientos sobre un espacio de soluciones posibles consiste en la selección iterativa de movimientos para transformar una solución hasta que se cumpla cierto criterio de parada. El criterio de parada determina cuándo se considera resuelto el problema sin que sea necesario disponer, en una situación intermedia, de información de lo cerca que se está de solucionarlo. Sin embargo, las búsquedas inteligentes deben utilizar este y otro tipo de información en el criterio de parada y en la selección de los movimientos.
En los **problemas de optimización**, la selección de movimientos y el criterio de parada se realizan teniendo en cuenta uno, o más, indicadores de la calidad de las soluciones encontradas en el recorrido. La evaluación de la calidad de las soluciones se realiza a través de una o varias funciones objetivo, teniendo en cuenta las restricciones del problema (si es más de una, se denomina **optimización multiobjetivo**). Los objetivos se formalizan por una o varias funciones que hay que maximizar o minimizar (supondremos, en la descripción de los métodos de solución, que se trata de maximizar). La estrategia de búsqueda establece los criterios y mecanismos que guiarán el recorrido, y puede incorporar herramientas de una o varias metaheurísticas junto a heurísticas específicas para el problema.
Los problemas de optimización aparecen de forma habitual en muchísimos campos científicos y su solución es de crucial importancia para el éxito de multitud de tareas de Inteligencia Artificial.
El problema se formaliza por medio de un espacio de soluciones $S$ y la función objetivo $f$. Resolver el problema de optimización $(S,f)$ consiste en **determinar una solución óptima**, es decir, una solución factible $x_o \in S$ tal que $f(x) \leq f(x_o)$, para cualquier $x \in S$.
Las soluciones alternativas se pueden expresar por la asignación de valores a algún conjunto finito de variables $X = \{X_i : i = 1,2,\dots,n\}$. Si se denota por $U_i$ al **dominio** (conjunto de los valores posibles) de cada una de estas $n$ variables, el problema consiste en seleccionar el valor $x_i$ asignado a cada variable $X_i$ del dominio $U_i$ que, sometido a ciertas restricciones, optimiza la función objetivo $f$. El universo de soluciones se identifica con el conjunto: $$U = U_1 \times\dots\times U_n = \{x = (x_i : i = 1,2,\dots,n) : x_i \in U_i\}$$
Las restricciones del problema reducen el universo de soluciones a un subconjunto de soluciones $S \subseteq U$, denominado **espacio factible**.
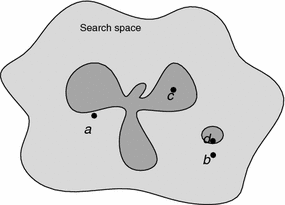
Los **procedimientos de búsqueda por entornos** recorren el espacio de soluciones mediante un conjunto de transformaciones o movimientos. Las soluciones que se obtienen de otra mediante uno de los movimientos posibles se denominan **vecinas** de ésta y constituyen su **entorno**. El conjunto de movimientos posibles da lugar a una relación de vecindad y una estructura de entornos en el espacio de soluciones cuya elección es un aspecto trascendental en el éxito de los procesos de búsqueda. Además de una implementación y evaluación eficiente de los movimientos, las propiedades de la estructura de entornos resultante intervienen en esta elección.
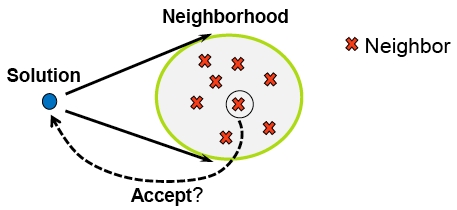
El entorno de una solución está constituido por las soluciones a las que se puede acceder desde ella por uno de los movimientos posibles. Formalmente, una estructura de entornos sobre un espacio o universo de búsqueda $U$ es una función $E : U \rightarrow {\mathcal P}(U)$ que asocia a cada solución $x \in U$ un entorno $E(x) \subseteq U$ de soluciones vecinas a $x$.
El esquema general de un procedimiento de búsqueda por entornos consiste en una ligera variante del esquema general de búsqueda anterior: generar una solución inicial y, hasta que se cumpla el criterio de parada, seleccionar iterativamente un movimiento para modificar la solución. Las soluciones son evaluadas mientras se recorren y se propone la mejor solución encontrada del problema.
En el proceso de creación de los movimientos se debe tener en cuenta que, aunque movimientos más complejos suponen un enriquecimiento de los entornos, con lo que se puede mejorar la aproximación al óptimo, se corre el riesgo de perjudicar la eficiencia del algoritmo al tener que contemplar un número mayor de movimientos posibles en el proceso de selección, o un mayor tiempo para calcular los vecinos de forma efectiva.
Otra característica importante de los movimientos es la factibilidad de las soluciones aportadas. Los **movimientos factibles** son aquellos que siempre proporcionan una solución factible, aquellas que tienen sentido en el problema, que están en $S$. Esto puede estar ligado o no al hecho de que se aplique sólo a soluciones factibles. En muchos casos, aplicar movimientos más simples, pero no necesariamente factibles, y descartar las soluciones producidas que no sean factibles, es menos eficiente que adaptar el diseño de los movimientos para que sean factibles, sobre todo cuando dicha comprobación es costosa o cuando la probabilidad de que resulte factible es baja. Formalmente, los procedimientos que sólo consideran movimientos factibles están asociados al concepto, algo más restrictivo, de estructura de entornos como una función $E : S \rightarrow \mathcal{P}(S)$ que asocia a cada solución factible $x\in S$ un entorno $E(x) \subseteq S$ de soluciones factibles vecinas a $x$.
Existen otras cuestiones relevantes en el éxito del procedimiento de búsqueda por entornos. Aparte de la selección de la propia estructura de entornos sobre la que articular la búsqueda, hay que valorar: la evaluación de la función objetivo, el procedimiento de generación de la solución inicial, y el criterio de parada.
La posibilidad de realizar una evaluación eficiente de la solución obtenida tras el movimiento es especialmente importante en aquellos problemas en los que la evaluación de la función objetivo sea costosa. Se pueden aplicar técnicas de **metaheurísticas con relajación** para evitar cómputos excesivos en la obtención de valoraciones exactas que no son imprescindibles en la conducción de la búsqueda. Además, se puede contar con procedimientos que evalúan la calidad de los movimientos sin tener que realizar una evaluación completa de la nueva solución desde cero. Para ello se utilizan procedimientos que actualizan rápidamente el valor de la función objetivo tras el movimiento, utilizando el valor anterior y los cambios producidos por el movimiento.
Las pautas de las **metaheurísticas constructivas** se utilizan para el diseño del procedimiento de generación de la solución inicial. En este sentido, las características fundamentales son la calidad y dispersión de las soluciones iniciales desde la que iniciar la búsqueda.
Por último, otra cuestión importante que afecta a cualquier procedimiento de solución de un problema emanado de una metaheurística de búsqueda por entornos es la condición de parada. Los criterios más corrientes suelen estar relacionados con limitar el número de iteraciones, de movimientos, de operaciones elementales o del tiempo de cómputo total o sin que se produzca alguna mejora.
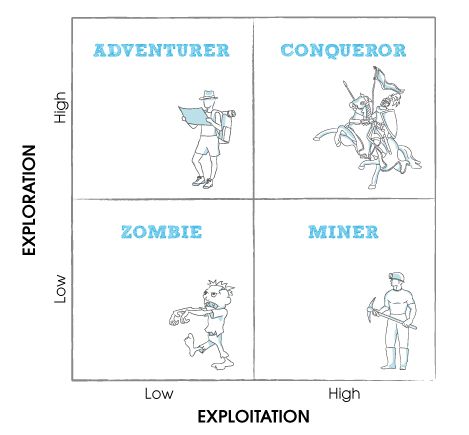
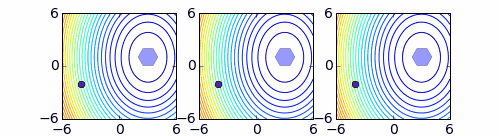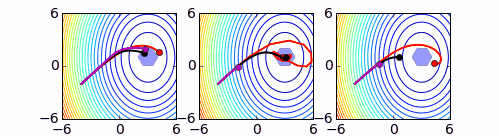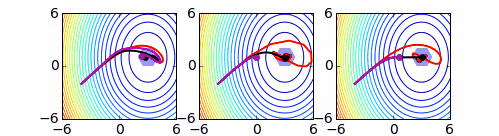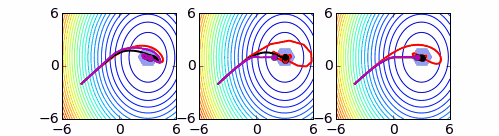
Dos características fundamentales en el procedimiento de búsqueda por entornos son las capacidades de **exploración** y de **explotación**. La exploración se refiere a la capacidad del método para explorar las diferentes regiones del espacio de búsqueda para encontrar la zona en la que se encuentra la solución del problema. La explotación de la búsqueda se refleja en el esfuerzo y capacidad por mejorar las soluciones con las que trabaja el procedimiento. Existe un amplio consenso en que estas dos características deben modularse adecuadamente para conseguir el éxito práctico de las aplicaciones de las metaheurísticas, que deben conseguir un equilibrio entre ambas.
## Búsquedas Locales
El término *local* se emplea con bastante frecuencia en los estudios teóricos y prácticos del campo de las metaheurísticas de búsqueda. Las estructuras de entorno suelen reflejar algún concepto de proximidad o vecindad entre las posibles soluciones del problema. Por tanto, el análisis del entorno de la solución actual en el recorrido de búsqueda para decidir cómo continuarla representa un estudio local del espacio de búsqueda.
Así pues, una **búsqueda local** es un proceso que, dada la solución actual en la que se encuentra el recorrido, selecciona iterativamente una solución de su entorno. Las metaheurísticas de búsqueda local establecen pautas de selección de esta solución del entorno de la solución actual dando lugar a búsquedas locales heurísticas con alto rendimiento. Las **búsquedas locales no informadas** sólo tienen en cuenta la estructura de entornos para guiar la búsqueda. Las **búsquedas monótonas** utilizan la evaluación de la función objetivo para admitir sólo cambios en la solución actual que supongan una mejora. Por tanto, las búsquedas locales monótonas quedan atrapadas al llegar a una solución que no admite mejora dentro de su entorno. Las **búsquedas globales** emplean diversos métodos para escapar de esta situación. A continuación analizamos los aspectos más relevantes de las metaheurísticas para estos procedimientos.
### Búsquedas No Informadas
Las estrategias de **búsqueda por entornos no informadas** son aquellas búsquedas locales que sólo prestan atención a la estructura de entornos en el espacio de búsqueda y no utilizan información acerca del valor de la función objetivo en las soluciones encontradas. Las metaheurísticas de búsqueda por entornos **exhaustiva**, **parcial** y **aleatoria** son las metaheurísticas de búsqueda no informadas más usuales.

Un **recorrido exhaustivo** de un espacio de búsqueda es el que incluye todos y cada uno de los elementos del espacio. Si el espacio de búsqueda es finito y no excesivamente grande, un procedimiento rudimentario para resolver el problema consiste en implementar un recorrido exhaustivo hasta encontrar la solución. En un problema de optimización, la búsqueda exhaustiva consiste en realizar un recorrido exhaustivo del espacio de soluciones del problema y tomar la mejor de ellas. Un recorrido exhaustivo del espacio se consigue empleando una ordenación (implícita o explícita) de todas las soluciones del espacio y utilizando una transformación que obtenga en cada iteración la solución siguiente en dicha ordenación. El procedimiento de generación de la solución inicial debe proporcionar la primera solución de dicha ordenación y el criterio de parada detectar cuándo se ha completado todo el espacio de búsqueda. La ordenación puede comprender sólo las soluciones factibles o un conjunto que las contenga. En este caso sólo habrá que considerar las soluciones factibles para elegir la mejor. A partir de la representación de las soluciones del espacio se determina la ordenación natural consistente en ir modificando sucesivamente los elementos que componen la solución. Dada una estructura de entornos para un problema, la **búsqueda por entornos exhaustiva** recorrerá sucesivamente y de forma exhaustiva los entornos de las soluciones visitadas. Si la estructura de entornos enlaza todas las soluciones del espacio, la búsqueda será exhaustiva, pero será necesario evitar o controlar las repeticiones para impedir que se entre en un ciclo indefinidamente.
En algunas circunstancias puede ser suficiente examinar sólo una parte del espacio de búsqueda para obtener una visión global de todo el espacio. Las **metaheurísticas de búsqueda parcial** establecen las pautas para organizar la selección de las soluciones a examinar. Para un problema de optimización, la búsqueda parcial aportará la mejor entre las soluciones examinadas como propuesta de solución. Si las soluciones a examinar se seleccionan de forma completamente al azar se trata de una búsqueda parcial aleatoria pura, conocida como **método de Monte Carlo**. La **metaheurística de búsqueda por entornos aleatoria** consiste en seleccionar iterativamente al azar una solución del entorno de la solución actual.
### Búsquedas Locales Monótonas
Las metaheurísticas de búsqueda anteriores no utilizan la información proporcionada por la evaluación de la función objetivo en la conducción de la búsqueda. Las estrategias de búsqueda pueden incorporar esta información al método de búsqueda para guiar los movimientos aplicados. Las **búsquedas informadas** son aquellas que, explícita o implícitamente, utilizan información de la evaluación de la función objetivo. Las **búsquedas locales (o por entornos) informadas** son las que utilizan información de la función objetivo sólo en el entorno de la solución actual.
Las **búsquedas monótonas** sólo aceptan mejoras de la solución que realiza el recorrido. Las **búsquedas locales monótonas** son las búsquedas locales que sólo aplican movimientos que mejoren la solución actual del recorrido. Las **búsquedas monótonas no estrictas** aceptan también nuevas soluciones que igualan a la solución actual. Estas estrategias presentan la ventaja de que pueden escaparse de las mesetas o zonas llanas del espacio de búsqueda, pero tienen el inconveniente de que podría caer en un ciclo indefinidamente dentro de una de tales mesetas.
La metaheurística básica de **búsqueda por entornos monótona aleatoria** consiste en seleccionar iterativamente una solución al azar del entorno de la solución actual que es sustituida por ésta si se produce una mejora. La solución de partida se puede obtener por cualquier procedimiento arbitrario y el criterio de parada reflejará el estancamiento de la búsqueda en un mínimo local presumible cuando en un cierto número de intentos no se pueda mejorar la solución actual. Las metaheurísticas intensifican la búsqueda en torno a cada solución actual seleccionando la mejor de entre una serie de soluciones del entorno obtenidas por un procedimiento del mismo tipo. La **intensidad de la búsqueda** viene dada por el número o la proporción de soluciones vecinas de la solución actual entre las que se toma la mejor. La **metaheurística de intensificación oscilante** consiste en hacer oscilar sistemáticamente entre dos valores extremos la intensidad de la búsqueda. La **metaheurística de intensificación oscilante dinámica** regula dinámicamente la intensidad de la búsqueda para intensificarla, hasta hacerla exhaustiva al acercarse al óptimo local, pero sin necesidad de encontrar la mejor solución vecina al comenzar los ascensos. Una estrategia autónoma para esta regulación dinámica es, por ejemplo, aumentarla cada vez que no se mejore la solución, hasta alcanzar el tamaño del entorno, y disminuirla mientras se produzcan esas mejoras, sin llegar a anularla.
Las **metaheurísticas de búsqueda local exhaustiva** maximizan el poder de explotación de la búsqueda local al examinar, si es necesario, todo el entorno de la solución actual. Las metaheurísticas voraz y ansiosa aparecen al aplicar las dos reglas fundamentales de selección de esta solución. La **metaheurística voraz** (**Greedy**) con la regla de selección de *el mejor primero* y la **metaheurística ansiosa** (**Anxious**) con la regla de selección de *el primero mejor*. En la primera de ellas se selecciona siempre la mejor solución del entorno de la solución actual y en la segunda se selecciona la primera solución del entorno que mejore la solución actual. En la metaheurística por entornos voraz se recorren siempre todas las soluciones del entorno para seleccionar la mejor, mientras que en la metaheurística por entornos ansiosa se detiene el recorrido cuando se encuentre una solución del entorno mejor que la actual, pero el recorrido se continúa de forma exhaustiva si no se encuentra tal mejora.
## Búsquedas Globales
El principal inconveniente de las búsquedas locales es que si se aproximan a una solución localmente óptima (una solución que es mejor que cualquiera de las de su entorno) la solución actual queda atrapada en su entorno. La regla de parada en las búsquedas monótonas implica detectar los mínimos locales analizando cuándo no se mejora la solución actual. Una búsqueda con una perspectiva global del espacio de soluciones debe buscar herramientas para escapar de estas situaciones.
Las principales **metaheurísticas de búsqueda global** surgen de las tres formas principales de escapar de esta situación:
- volver a comenzar la búsqueda desde otra solución inicial,
- modificar la estructura de entornos, y
- permitir movimientos de empeoramiento de la solución actual.
Estas tres opciones dan lugar, respectivamente, a la **metaheurística con arranque múltiple**, a la **metaheurística de entorno variable** y a la **metaheurística de búsqueda no monótona**:
- Los procedimientos de **búsqueda con arranque múltiple** (**Multi-Start**) realizan varias búsquedas monótonas partiendo de diferentes soluciones iniciales. La búsqueda monótona implicada puede ser cualquiera de las anteriormente descritas. Una de las formas más simples de llevar esto a cabo consiste en generar una muestra de soluciones iniciales. Esto es equivalente a generar al azar una nueva solución de partida cada vez que la búsqueda queda estancada en el entorno de una solución óptima local.
- La **Búsqueda por Entornos Variables** (**Variable Neighborhood Search**, **VNS**) es una metaheurística que consiste en cambiar de forma sistemática la estructura de entorno. La idea original fue considerar distintas estructuras de entornos y cambiarlas sistemáticamente para escapar de los mínimos locales. El algoritmo básico obtiene una solución del entorno de la solución actual, ejecuta una búsqueda monótona local desde ella hasta alcanzar un óptimo local, que reemplaza a la solución actual si ha habido una mejora y modifica la estructura de entorno en caso contrario.

- Con las **metaheurísticas de búsqueda probabilísticas** se selecciona aleatoriamente un vecino de la solución actual que la reemplaza con cierta probabilidad, por ejemplo, con probabilidad 1 si tiene mejor valor objetivo, y con una probabilidad menor que 1 si su valor objetivo es peor. Si el número de iteraciones es elevado, la búsqueda puede escapar de cualquier óptimo local si la probabilidad de aceptar peores soluciones va decreciendo. Generalmente la probabilidad de aceptar una solución peor es función del empeoramiento de forma que, a menor diferencia en el valor objetivo, hay mayor probabilidad de ser aceptada. El **Templado Simulado** es el caso más importante de las metaheurísticas de búsqueda global con criterio de aceptación probabilístico. Se usa una probabilidad de aceptación de nuevas soluciones peores que es función exponencial de la modificación de la función objetivo.
Otras metaheurísticas simplemente reducen o incrementan esta probabilidad para modular la exploración y explotación de la búsqueda. Las **metaheurísticas de umbrales de aceptación** (**Threshold Accepting**) aceptan las nuevas soluciones peores que no sobrepasen el umbral y modulan este umbral con el mismo propósito.

- Las **metaheurísticas de búsqueda con memoria**, representada por la **Búsqueda Tabú**, comprenden las estrategias que tratan de utilizar la memoria del proceso de búsqueda para mejorar su rendimiento. Está fundamentada en las ideas expuestas por F. Glover en 1986, y en el origen del método el propósito era sólo evitar la reiteración en una misma zona de búsqueda recordando las últimas soluciones recorridas. Sin embargo, posteriormente se han realizado diversas propuestas para rentabilizar la memoria a medio o largo plazo. La forma más directa de introducir la memoria en el procedimiento de búsqueda no monótona es considerar una función de aceptación que tenga en cuenta la historia de la búsqueda. El procedimiento elemental de búsqueda tabú evita la repetición prematura de las mismas soluciones en el recorrido, para lo que prohíbe que las últimas soluciones vuelvan a utilizarse en el recorrido de búsqueda.
Estas estrategias se pueden aplicar dentro de la estructura de la búsqueda general de dos formas: introduciendo una función de aceptación que determine cuándo se acepta la nueva solución generada o modificando el procedimiento de generación del movimiento a aplicar a la solución actual. Con la primera de estas alternativas la función de aceptación puede incluir en sus parámetros información referente a la historia y el estado de la búsqueda, y a la solución generada. En el segundo caso, el procedimiento de generación de movimiento debe tener un diseño en el que se generan las soluciones vecinas de acuerdo con algún criterio que tenga en cuenta información de la historia y el estado de la búsqueda.
La **Búsqueda Reactiva** (**Reactive Search**) es una metaheurística que propone usar, dentro de la búsqueda tabú, la información a largo plazo obtenida del recorrido. Se persigue detectar indicios de que la búsqueda necesita incrementar su exploración, por la repetición de ciertas estructuras o patrones en las soluciones recientemente visitadas. Esta información se almacena y se accede a ellas utilizando técnicas eficientes de dispersión (hashing) o de árboles de búsqueda usuales en gestión de grandes cantidades de datos. Según la información que se tenga almacenada en cada iteración se activa un proceso reactivo para alejarse de la zona de estancamiento.

## Búsquedas Basadas en Poblaciones
En una **búsqueda en grupo o basada en poblaciones** se sustituye la solución actual que recorre el espacio de soluciones por un conjunto de soluciones que lo recorren conjuntamente interactuando entre ellas. Además de los movimientos aplicables a las soluciones que forman parte de este conjunto, denominado *grupo o población de búsqueda*, se contemplan otros operadores para generar nuevas soluciones a partir de las ya existentes.
Las estrategias de búsqueda en grupo se iniciaron con el famoso **Algoritmo Genético**. En la actualidad adoptan diversas características, como se puede observar en la gran cantidad de trabajos publicados sobre este tipo de procedimientos.
Las cuestiones fundamentales de su implementación para la solución de problemas de optimización son:
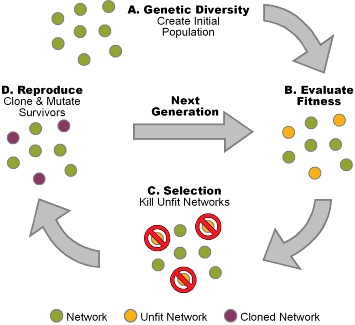
En primer lugar, se establece una codificación apropiada de las soluciones del espacio de búsqueda y una forma de evaluar la función objetivo para cada una de estas codificaciones. Las soluciones se identifican con individuos que pueden formar parte de la población de búsqueda. La codificación de una solución se interpreta como el cromosoma del individuo compuesto de un cierto número de genes a los que les corresponden ciertos alelos. Se consideran dos operaciones básicas: la mutación y el cruce. La mutación de un individuo consiste en modificar un gen cambiando, al azar, el alelo correspondiente. El cruce de dos individuos (llamados padres) produce un individuo hijo tomando un número $k$ (elegido al azar) de genes de uno de los padres y el resto del otro. La población evoluciona de acuerdo a las estrategias de selección de individuos, tanto para las operaciones como para la supervivencia. La selección se puede hacer simulando una lucha entre los individuos de la población con un procedimiento que, dados dos individuos selecciona uno de ellos teniendo en cuenta su valoración (la función objetivo) y la adaptación al ambiente y a la población (criterios de diversidad, representatividad). La lucha por la supervivencia tiene por objeto mantener controlado el tamaño de la población. La selección de los luchadores se puede hacer de diferentes maneras: dos individuos seleccionados al azar, cada nuevo individuo con otro seleccionado al azar o con el peor de los existentes, etc. Entre las metaheurísticas derivadas de los algoritmos genéticos destacan los Algoritmos meméticos, que surgen de combinar los algoritmos genéticos con búsquedas locales.
Los **Algoritmos de Estimación de Distribuciones** (**EDA**) son algoritmos evolutivos que usan una colección de soluciones candidatas para realizar trayectorias de búsqueda evitando mínimos locales. Estos algoritmos usan la estimación y simulación de la distribución de probabilidad conjunta como un mecanismo de evolución, en lugar de manipular directamente a los individuos que representan soluciones del problema. Un algoritmo EDA comienza generando aleatoriamente una población de individuos. Se realizan iterativamente tres tipos de operaciones sobre la población. El primer tipo de operación consiste en la generación de un subconjunto de los mejores individuos de la población. En segundo lugar se realiza un proceso de aprendizaje de un modelo de distribución de probabilidad a partir de los individuos seleccionados. En tercer lugar se generan nuevos individuos simulando el modelo de distribución obtenido. El algoritmo se detiene cuando se alcanza un cierto número de generaciones o cuando el rendimiento de la población deja de mejorar significativamente.
El enfoque de la **metaheurística de Búsqueda Dispersa** (o **Scatter Search**) contempla el uso de un conjunto de referencia de buenas soluciones dispersas que sirve tanto para conducir la búsqueda, mejorando las herramientas para combinarlas adecuadamente, como para mantener un grado satisfactorio de diversidad. La propuesta inicial se originó en estrategias para crear reglas de decisión compuestas. La Búsqueda Dispersa se distingue de otros procedimientos en los mecanismos de intensificación y diversificación que explotan la memoria adaptada recurriendo a los fundamentos que unen el Scatter Search a la Búsqueda Tabú.
El **reencadenamiento de caminos** (**Path Relinking**) es una metaheurística asociada a la búsqueda dispersa que utiliza la información que se obtiene de las mejores soluciones. Básicamente, se trata de generar soluciones explorando las trayectorias que conectan soluciones de alta calidad. Partiendo de una de estas soluciones se genera un camino de soluciones hacia la otra solución incorporando a la primera atributos de la segunda. Este camino se construye tomando cada vez el atributo de la segunda solución que lo hace más cercano a ella. A continuación se toman, como puntos de arranque para nuevas fases de mejora, una o varias de las soluciones del recorrido anterior.
## Otras Metaheurísticas de Búsqueda y Optimización
Se han propuesto otras metaheurísticas de relevancia, algunas de las cuales presentan como novedad estar inspiradas en distintos fenómenos de la naturaleza. Entre ellas destacan las redes neuronales, las colonias de hormigas, las bandadas de aves o bancos de peces. Otras metaheurísticas tienen el mérito de aplicar herramientas muy exitosas en otros campos de la IA, como la metaheurística FANS o los métodos inteligentes de realizar búsqueda locales.
Las **redes neuronales artificiales** surgieron como modelos abstractos de sistemas nerviosos naturales formados por unidades de cómputo, llamadas neuronas, interconectadas. Estos modelos tienen la capacidad de ajustar sus parámetros en respuesta a unas entradas y salidas mejorando alguna función. Asociando los estados de la red a soluciones de un problema y utilizando el objetivo como referente, consiguen aproximarse al estado que corresponde con la solución óptima. Otros modelos basados en redes neuronales aplicados con éxito a problemas de optimización combinatoria son las **máquinas de Boltzman** y las **redes competitivas WTA**.

La **metaheurística de sistemas de hormigas** (**Ant Systems**) emplea estrategias inspiradas en el comportamiento de las colonias de hormigas para descubrir fuentes de alimentación, al establecer el camino más corto entre éstas y el hormiguero y transmitir esta información al resto de sus compañeras.
La **optimización extrema o extremal** (**EO**, **Extreme Optimization**) es una metaheurística inspirada en procesos auto-organizativos frecuentemente encontrados en la naturaleza. La idea central es utilizar modelos de evolución de ecosistemas que, en lugar de seleccionar los mejores elementos, llevan a la extinción a las componentes mal adaptadas del sistema. La idea básica del método es eliminar sucesivamente las componentes extremadamente indeseables de las soluciones subóptimas. El método actúa sobre una única solución, y no sobre un conjunto de soluciones o población como los algoritmos genéticos, modificando el atributo de menor nivel de adaptación (y aquellos afectados por este cambio) aplicando algún tipo de transformación o movimiento.
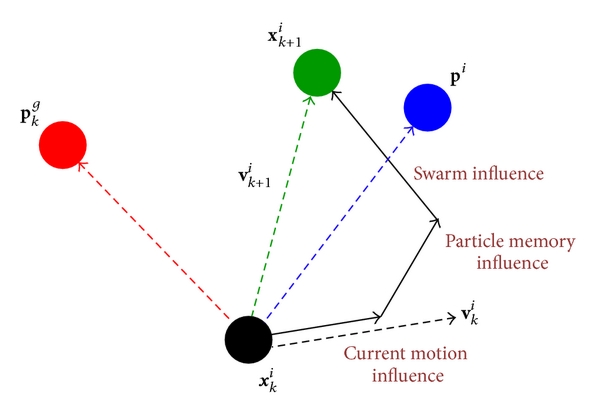
La **optimización por enjambres de partículas** (**PSO**, **Particle Swarm Optimization**) es una metaheurística evolutiva inspirada en el comportamiento social de las bandadas de pájaros, bancos de peces, o colonias de abejas. Las soluciones, llamadas partículas, se desplazan en el espacio de búsqueda guiadas por la partícula que mejor solución ha encontrado hasta el momento y que hace de líder de la bandada. Cada partícula evoluciona teniendo en cuenta la mejor solución encontrada en su recorrido y al líder. En cada iteración, las partículas modifican su velocidad hacia la mejor solución de su entorno teniendo en cuenta la información del líder.
Otras metaheurísticas son la **Búsqueda Local Iterada**, la **metaheurística de concentración**, la **metaheurística de búsqueda local guiada**, la **metaheurística con ruido** (**Noising Methods heuristics**), la **metaheurística de perturbación**, o la **metaheurística de búsqueda fuzzy**.
La **programación por restricciones** (**Constraint Programming**), de la que veremos ejemplos y algoritmos en unidades posteriores, puede considerarse una metaheurística muy general que constituye un paradigma propio dentro de las metaheurísticas, donde lo más relevante es la atención que se le presta al tratamiento de las restricciones que surgen en un problema y cómo afecta a los procedimientos de búsqueda de soluciones.