**SVRAI**
Teoría de Juegos II
Juegos Cooperativos: Coaliciones
Existe otro tipo de juego estudiado en la teoría de juegos en donde los agentes deciden cómo formar coaliciones entre ellos y cada coalición recibe alguna utilidad. Por ejemplo, un grupo de personas, cada una con diferentes habilidades, quiere crear nuevas empresas. El problema al que se enfrentan es decidir cómo dividirse en subgrupos de forma que cada subgrupo tenga el conjunto de habilidades necesario para tener éxito en el mercado. O también, un grupo de agentes con diferentes habilidades debe decidir cómo dividirse en subgrupos para gestionar el mayor número posible de tareas de la manera más eficiente. Como los agentes deben cooperar entre sí para formar coaliciones y un agente no puede decidir unilateralmente que formará una coalición con un segundo agente, estos juegos se conocen como juegos cooperativos.
Es interesante observar que la mayoría de los libros de texto de Teoría de Juegos se centran exclusivamente en los juegos no cooperativos, ya que éstos han encontrado muchas aplicaciones en la economía y la empresa y han sido el centro de la mayor parte de la investigación. Sin embargo, a la hora de construir sistemas multiagente, encontramos que los juegos cooperativos son mucho más útiles, ya que modelan de forma clara e inmediata el problema de qué agentes deben realizar qué tareas y establecen unos mínimos de comunicación, coordinación y acuerdo entre los agentes involucrados.
Las técnicas de teoría de juegos se han impuesto recientemente en muchas aplicaciones de ingeniería, especialmente en las comunicaciones. Con la aparición de la cooperación como nuevo paradigma de comunicación, y la necesidad de redes autoorganizadas, descentralizadas y autónomas, se ha hecho imperativo buscar herramientas teóricas de juegos adecuadas que permitan analizar y estudiar el comportamiento y las interacciones de los nodos de estas redes. En este contexto, podemos justificar los conceptos de la teoría de juegos cooperativos, concretamente los juegos coalicionales, en sus potenciales aplicaciones en redes de comunicación e inalámbricas, que se convierten entonces en un ejemplo paradigmático y muy actual en el que aplicar y sacar provecho de las teorías desarrolladas.
# Introducción
Como comentamos en el [capítulo anterior](TeoriaJuegosNoCoop.md.html), la **Teoría de Juegos** en general proporciona un marco analítico formal con un conjunto de herramientas matemáticas para estudiar las (complejas) interacciones entre jugadores racionales. Lo que empezó como una curiosidad matemática ha tenido, con el paso del tiempo, un impacto revolucionario en un gran número de disciplinas que van desde la ingeniería, la economía y las ciencias políticas, hasta la filosofía o incluso la psicología [#Myerson]. Desde hace unos años se ha producido un crecimiento significativo de las actividades de investigación que utilizan la teoría de juegos para analizar las redes de comunicación debido, principalmente, a:
* la necesidad de desarrollar redes móviles autónomas, distribuidas y flexibles en las que los dispositivos de la red puedan tomar decisiones estratégicas independientes y racionales; y
* la necesidad de contar con algoritmos distribuidos de baja complejidad que puedan representar de forma eficiente escenarios de competencia o colaboración entre entidades de la red.
Como vimos en el capítulo anterior, la **Teoría de Juegos No Cooperativos** estudia las elecciones estratégicas resultantes de las interacciones entre jugadores que compiten entre sí, donde cada jugador elige su estrategia de forma independiente para mejorar su propio rendimiento (**utilidad**) o reducir sus pérdidas (**costes**). Para resolver los juegos no cooperativos se han desarrollado a lo largo de los años diversas herramientas, como diversos **conceptos de solución** y caracterización de distintos tipos de **equilibrio**.
En contraposición, la **Teoría de Juegos Cooperativos** proporciona herramientas analíticas para estudiar el comportamiento de los jugadores racionales cuando cooperan. La rama principal de los juegos cooperativos describe la formación de grupos de jugadores que cooperan, denominados **coaliciones**, que pueden fortalecer las posiciones de los jugadores en el juego. Por ello, y como primera aproximación, nos centraremos aquí en la teoría de **juegos de coalición**, aunque no son los únicos juegos cooperativos que existen, y en muchas referencias podemos encontrar otros tipos de juegos, como la **juegos de negociación**.
!!!
Entre las características generales de los juegos de coalición destacamos:
* Partimos de un conjunto de jugadores y estudiamos los incentivos a formar subgrupos.
* Los acuerdos entre las posibles coaliciones son de obligatorio cumplimiento (de la misma forma que en la solución de Nash al problema de negociación, en este sentido, toda asignación de utilidades es un equilibrio).
* Luego la pregunta fundamental es qué coaliciones se formarían que respeten los acuerdos.
Los juegos de coalición resultan ser una herramienta muy poderosa para diseñar estrategias de cooperación justas, robustas, prácticas y eficientes, y siguiendo [#Saad] podemos agruparlos en las siguientes tres clases distintas:
1. Clase I: **Juegos Canónicos**.
2. Clase II: **Juegos de Formación**.
3. Clase III: **Juegos de Grafos**.
Aunque en esta breve introducción nos centraremos más en la primera clase, intentaremos dar las características y diferencias más importantes también de las otras dos clases. Para ello, comenzaremos por una sección general que introduce formalmente algunos de los conceptos transversales de la **Teoría de Juegos Coalicionales**.
# Juegos Coalicionales
En esencia, los **juegos coalicionales** implican a un conjunto de jugadores, denotados por $N=\{1,\dots,n\}$, que buscan formar grupos cooperativos, es decir, **coaliciones**, para fortalecer sus posiciones en el juego. Toda coalición representa un acuerdo entre los jugadores para actuar como una sola entidad. La formación de coaliciones o alianzas es omnipresente en muchas aplicaciones. Por ejemplo, en los juegos políticos, los partidos o los individuos pueden formar coaliciones para mejorar su poder de voto. Además del conjunto de jugadores, el segundo concepto fundamental de un juego de coalición es el **valor de la coalición**, denotado por $v$ (juega un papel similar al de **utilidad** en los juegos no cooperativos). La definición concreta del valor de coalición determinará la forma y el tipo de juego. No obstante, independientemente de la definición del valor, un juego coalicional se define de forma única por el par $(N,v)$.

!!!Tip:Ejemplos
1. **Juegos de compartir beneficios**: personas con talentos complementarios pueden considerar unirse para un proyecto. En este caso puede no ser obvio cómo, dada una coalición, se repartirían los beneficios entre los que la forman.
2. **Juegos coalicionales simples**: son juegos en los que $v(S) \in \{0, 1\}$. Decimos que una coalición $S$ es ganadora si $v(S)= 1$. Un ejemplo de juegos coalicionales simples son los juegos de votación. En este caso $v(S) = 1$ representa que la coalición puede pasar una proposición sujeta a votación. Por ejemplo, en el Consejo de Seguridad de las Naciones Unidas $v(S) = 1$ si y solo si $|S|\geq 9$ y además, todos los miembros permanentes están en $S$ (los miembros permanentes son: Estados Unidos, Francia, Inglaterra, China y Rusia).
3. **Juegos de voto mayoritario por pesos** (este es una caso particular de juegos simples): Decimos que $(N,v)$ es un juego de este tipo si existe una cuota $q\geq 0$ y un vector de pesos $w \in \mathbb{R}_+^{|N|}$ tal que: $v(S) = 1$ si y sólo si $\sum_{i\in N}w_i\geq q$. Por ejemplo, en el mecanismo de votación del parlamente inglés, el número de miembros es $650$. Para pasar una proposición se necesitan $326$ votos a favor. Supongamos que existen tres partidos que votan en bloque cada uno con $|P_1|=282$, $|P_2|=260$, y $|P_3|=108$ miembros, respectivamente. Como ningún partido tiene una mayoría $v(P_1) = v(P_2) = v(P_3) = 0$. Sin embargo, cualquier coalición de dos o tres partidos puede pasar una proposición. Este sistema de votación, que emite voto único por partidos, es un sistema de votación por pesos donde $q = 326$, y $w = (282, 260, 108)$. Todo juego de voto mayoritario por pesos es simple (el recíproco no es cierto).
4. **Juegos de asignación de costos**: se necesita construir una nueva pista en un aeropuerto. La pregunta fundamental es cómo cobrarle a los diferentes vuelos por la utilización de la pista teniendo en cuenta el uso que hacen de ella y las necesidades que tienen (en este caso lo jugadores son los diferentes vuelos). Explicitaremos este juego con detalle más adelante.
!!!def:Definición (Juegos Coalicionales)
Un **Juego coalicional** es un par $(N,v)$ dado por un conjunto $N=\{1,\dots,n\}$ de jugadores y una función $v$ que mide el **valor de la coalición**:
1. Si $v : 2^N \to \mathbb{R}$ se dice que es un **juegos con utilidad transferible** (**UT**).
2. Si $v$ no es una función real, sino que devuelve un conjunto de vectores de retribución, $v(S)\subseteq \mathbb{R}^{|S|}$, se dice que es un **juegos con utilidad no transferible** (**UNT**).
(Recordemos que $2^A=\mathcal{P}(A)$ es el conjunto de todos los subconjuntos de $A$).
La forma más común de un juego coalicional es la **forma característica**, según la cual el valor de una coalición $S$ depende únicamente de los miembros de esa coalición, sin depender de cómo se estructuran los jugadores en $N \setminus S$. La forma característica fue introducida por von Neuman y Morgenstern en [#Neumann] en el marco de una categoría de juegos coalicionales conocida como **juegos con utilidad transferible** (**UT**), donde el valor es una función $v : 2^N \to \mathbb{R}$ (**función característica**). Esta función característica asocia a cada posible coalición $S\subseteq N$ un número real que cuantifica las ganancias de $S$. La propiedad UT implica que la utilidad total representada por este número real puede dividirse de cualquier manera entre los miembros de la coalición, se consideran valores que los miembros de la coalición pueden distribuir entre ellos utilizando una regla de equidad adecuada (por ejemplo, una de esas reglas es la distribución equitativa). La cantidad de utilidad que un jugador $i\in S$ recibe de la división de $v(S)$ constituye el pago del jugador y la denotaremos por $x_i$ en adelante. El vector $x\in \mathbb{R}^S$ en el que cada elemento $x_i$ es la retribución del jugador $i\in S$ constituye una asignación de retribución (recordemos que $A^B=\{f:B\to A\}$, en particular, $\mathbb{R}^S$ representa el conjunto de todas las funciones reales sobre el conjunto $S$, es decir, el conjunto de vectores de retribución alcanzables por el jugador en $S$).
!!!Tip: Ejemplo
El granjero $X$ produce $8\frac{1}{3}$ de toneladas de cierto cereal C. Por su parte, el granjero $Y$ produce $16\frac{2}{3}$ de toneladas del mismo cereal. En el mercado nacional, cuando se venden menos de $20$ toneladas, se pagan a $1200€$ cada una, y para tonelajes mayores el pago es de $2000€$. El señor $Z$ puede servir de intermediario entre agricultores y una empresa internacional que, a cambio de establecer un proceso extra durante la producción del cereal, paga la tonelada a $3200€$, aunque el mínimo de tonelaje que compra es de $20$. Si $X$ e $Y$ se unen a $Z$ para llevar a cabo la venta de su cereal, la situación se plantea como un juego cooperativo en donde $N = \{1, 2, 3\}$ ($1=X$, $2=Y$ y $3=Z$) y donde para todo $S \subseteq N$, $v(S)$ representa el monto obtenido por la venta del cereal cuando los jugadores en $S$ intervienen en la negociación, y se muestra en la siguiente tabla (en euros):
$$
\begin{array}{|c|c|c|c|c|c|c|c}
S & \{1\} & \{2\} & \{3\} & \{12\} & \{13\} & \{23\} & \{123\} \\
\hline
v(S)& 10K& 20K& 0& 50K& 0& 0& 80K
\end{array}
$$
El problema consiste ahora en repartir el monto obtenido por la venta del cereal entre los tres agentes que intervienen en el proceso de negociación ($X$, $Y$ y $Z$).
Aunque la función característica de los UT puede modelar una amplia gama de juegos, existen muchos escenarios en los que el valor de la coalición no puede asignarse a un único número real, o existen restricciones insalvables en la distribución de la utilidad. Estos juegos se conocen como **juegos de coalición con utilidad no transferible** (**UNT**) y fueron introducidos por primera vez por Aumann y Peleg en [#Aumann] utilizando como base los juegos estratégicos no cooperativos.
El valor de una coalición $S$ en un juego UNT, $v(S)$, ya no es una función sobre la recta real, sino un conjunto de vectores de retribución, $v(S)\subseteq \mathbb{R}^S$, donde para cada $x\in v(S)$, $x_i$ representa una retribución que el jugador $i\in S$ puede obtener dentro de la coalición $S$. Con esta definición, un juego UT puede verse como un caso particular del marco UNT.
!!!
Los juegos de utilidad transferible corresponden a situaciones donde los agentes pueden transferirse la utilidad de lo que puedan recibir de participar en una coalición (por ejemplo, valores monetarios, un bien divisible, etc.).
Utilidades no tranferibles son por ejemplo la reputación, influencia política, etc.
Recientemente, ha habido un interés creciente en los juegos coalicionales en los que el valor de una coalición depende de la partición de $N$ que se forma con la coalición. En tales juegos, a diferencia de la forma característica, el valor de una coalición $S$ tendrá una fuerte dependencia también de cómo se estructuran los jugadores en $N \setminus S$. Para ello, Thrall y Lucas en [#Thrall] introdujeron el concepto de **juegos en forma de partición**.
En estos juegos, dada una estructura de coaliciones, $\mathcal{B}$, definida como una partición de $N$ (es decir, $\mathcal{B}=\{B_1, \dots, Bk\}$, tal que $\forall i\neq j,\ B_i \cap B_j =\emptyset$, y $\bigcup_{i=1}^k B_i = N$), el valor de una coalición $S\in \mathcal{B}$ viene dado por medio de una función $v(S, \mathcal{B})$, que impone una dependencia entre el valor de evaluación de $S$ y la estructura coalicional considerada. Este tipo de juegos coalicionales son especialmente complejos de resolver, y también especialmente interesantes.
!!!Tip
Como ejemplo de la diferencia entre las formas características y de partición, consideremos un juego de cinco jugadores, $N=\{1, 2, 3, 4, 5\}$, y sea $S_1=\{1, 2, 3\}$, $S_2=\{4\}$, $S_3=\{5\}$ y $S_4=\{4, 5\}$. Dadas dos particiones, $\mathcal{B}_1=\{S_1, S_2, S_3\}$ y $\mathcal{B}_2=\{S_1, S_4\}$ de $N$, la evaluación del valor de la coalición $S_1$ depende de la forma del juego:
1. Si el juego está en forma característica, entonces $v(S_1,\mathcal{B}_1) = v(S_1,\mathcal{B}_2) = v(S_1)$,
2. Si está en forma de partición $v(S_1, \mathcal{B}_1)$ y $v(S_1, \mathcal{B}_2)$ no tienen porqué coincidir.
A diferencia de la forma característica, el valor de $S_1$ en la forma de partición depende de si los jugadores 4 y 5 están en la misma coalición o no (cooperan o no).
En muchos juegos coalicionales, los jugadores están interconectados y se comunican a través de enlaces particulares que dotan de estructura de grafo al conjunto. En tales escenarios, tanto la forma característica como la forma de partición pueden ser inadecuadas ya que en ambas formas el valor de una coalición es independiente de cómo estén conectados sus miembros. Para modelar este caso, Myerson introduce en [#Myerson2] los **juegos coalicionales en forma de grafo**, posteriormente generalizados en [#Jackson] haciendo que el valor de cada coalición $S\subseteq N$ sea una función de la estructura del grafo que conecta a los miembros de $S$. Por lo tanto, dado un juego coalicional $(N, v)$ y un grafo $G_S$ (dirigido o no dirigido) con vértices en los miembros de una coalición $S\subseteq N$, el valor de $S$ en forma de grafo viene dado por $v(G_S)$. Para los juegos en forma de grafo, el valor también puede depender del grafo $G_{N \setminus S}$ que interconecta a los jugadores en $N \setminus S$.

# Clase I: Juegos Canónicos
Dentro de esta clase está la categoría más popular de juegos coalicionales, y son los más estudiados, formalizados y con los conceptos de solución más claros. Para clasificar un juego como canónico, los principales requisitos son:
1. El juego coalicional está en forma característica (UT o UNT).
2. La cooperación, es decir, la formación de grandes coaliciones, nunca es perjudicial para ninguno de los jugadores implicados. Por lo tanto, en los juegos canónicos ningún grupo de jugadores puede obtener peores resultados cooperando. Esto se debe a la **propiedad de superaditividad** (que formalizaremos más adelante).
3. Bajo las condiciones del punto anterior, el principal objetivo de un juego canónico es estudiar las propiedades y la estabilidad de la **gran coalición** (la coalición de todos los jugadores del juego), y estudiar las ganancias resultantes de la cooperación con un coste despreciable o nulo, así como la distribución de estas ganancias de forma justa entre los jugadores.
Las dos primeras condiciones para clasificar un juego como canónico se refieren a las propiedades matemáticas del juego. En primer lugar, todo juego canónico debe tener una forma característica. En segundo lugar, el juego canónico debe ser **superaditivo**:
!!!def:Definición (Superaditividad)
Un juego coalicional, $(N,v)$, se dice **superaditivo** si verifica:
$$\forall S_1,S_2\subseteq N, S_1\cap S_2=\emptyset\ \Rightarrow \{x\in \mathbb{R}^{|S_1\cup S2|}:\ (x_i)_{i\in S_1} \in v(S_1), (x_j)_{j\in S_2}\in v(S_2)\}\subset v(S_1 \cup S_2)$$
!!!
Si usamos la notación de sumas de conjuntos, la superaditividad la podemos reescribir como:
$$\forall S_1,S_2\subseteq N, S_1\cap S_2=\emptyset\ \Rightarrow v(S_1)+v(S_2)\subset v(S_1 \cup S_2)$$
La superaditividad implica que, dadas dos coaliciones disjuntas $S_1$ y $S_2$, si se forma la coalición $S_1 \cup S_2$, ésta puede dar a sus miembros cualquier asignación que puedan lograr cuando actúan en $S_1$ y $S_2$ por separado.
Para un juego UT, la superaditividad se reduce a:
$$\forall S_1,S_2\subseteq N, S_1\cap S_2=\emptyset\ (v(S_1 \cup S_2)\geq v(S_1)+ v(S_2))$$

De donde se entiende mejor el concepto de juego superaditivo:
!!!
Un juego es superaditivo si la cooperación, es decir, la formación de una coalición a partir de coaliciones disjuntas, garantiza al menos el valor que obtienen las coaliciones disjuntas por separado.
La razón de ser de la superaditividad es que, dentro de una coalición, los jugadores siempre pueden volver a su comportamiento no cooperativo para obtener sus ganancias no cooperativas. Por tanto, en un juego superaditivo, la cooperación siempre es beneficiosa. Debido a la superaditividad en los juegos canónicos, es beneficioso para todos los jugadores formar siempre **la gran coalición**, $N$, es decir, la coalición de todos los jugadores, ya que la recompensa recibida de $v(N)$ es, al menos, tan grande como la cantidad recibida por los jugadores en cualquier partición de coaliciones que pudieran formar.
Por todo ello, la formación de la gran coalición en los juegos canónicos implica que el énfasis principal está en estudiar las propiedades de esta gran coalición. En los juegos canónicos son importantes dos aspectos:
1. Encontrar una asignación de pagos que garantice que ningún grupo de jugadores tenga incentivos para abandonar la gran coalición (es decir, tener una gran coalición estable), y
2. Evaluar las ganancias que puede obtener la gran coalición así como los criterios de equidad que deben utilizarse para distribuir estas ganancias (es decir, tener una gran coalición justa).
Para resolver estas necesidades introduciremos una serie de conceptos que se han ido refinando a lo largo de los últimos años.
## El Núcleo
El concepto de solución más conocido para los juegos coalicionales, y para los juegos clasificados como canónicos en particular, es el **núcleo**, que está directamente relacionado con la estabilidad de la gran coalición. En un juego coalicional canónico $(N, v)$, debido a la superaditividad, los jugadores no deben tener un incentivo para formar la gran coalición $N$. Por ello, el núcleo de un juego canónico se define como el conjunto de vectores de pagos que garanticen que ningún grupo de jugadores tenga un incentivo para abandonar $N$ y formar otra coalición $S\subset N$.
!!!def:Definición (Imputación)
Para un juego UT, una **imputación** es un vector de pagos, $x\in \mathbb{R}^N$, para la gran coalición que satisface:
1. Es **grupalmente racional**: $\sum_{i\in N} x_i =v(N)$.
2. Es **individualmente racional**: $x_i\geq v(\{i\})$, $\forall i \in N$ (cada jugador puede obtener un beneficio no menor que actuando solo).
!!!def:Definición (Núcleo)
El **núcleo** se define como el conjunto de imputaciones en las que ninguna coalición $S\subset N$ tiene un incentivo para rechazar la asignación de pagos propuesta por la gran coalición, desviarse de ella, y formar otra coalición $S$, es decir:
$$C_{UT} =\{x :\ \sum_{i\in N} x_i =v(N)\ \wedge\ \forall S\subseteq N\ (\sum_{i\in S}x_i \geq v(S))\}$$
El núcleo garantiza que estas desviaciones no se produzcan porque cualquier asignación de beneficios que esté en el núcleo garantiza, al menos, una cantidad de utilidad igual a $v(S)$ para cada $S\subset N$. Claramente, siempre que se pueda encontrar una asignación de beneficios que esté en el núcleo, entonces la gran coalición es una solución estable y óptima para el juego.
!!!def:Definición
Para resolver los juegos UNT utilizando el núcleo, se suele suponer que $v$ satisface lo siguiente para cualquier coalición $S$:
1. $v(S)$ es un subconjunto cerrado y convexo de $\mathbb{R}^S$.
2. $v(S)$ es **comprehensivo**, es decir: $\forall x\in v(S)\ \forall y\in \mathbb{R}^S\ (y\leq x \rightarrow y\in v(S))$.
3. El conjunto $\{x\in v(S):\ \forall i\in S\ (x_i\geq z_i)\}\subset \mathbb{R}^S$ es acotado (donde $z_i=\max\{y_j:\ y\in v(\{i\})\}\le \infty$, para cada $i\in N$).
La **propiedad de comprehensión** significa que si los miembros de una coalición $S$ pueden conseguir una determinada asignación de pagos, entonces, cambiando sus estrategias, los miembros de $S$ pueden conseguir cualquier asignación *menor*.
La última propiedad significa que, para una coalición $S$, el conjunto de pagos de $S$ en los que para cada jugador de $S$ se mejora lo mejor que ese jugador puede obtener de forma no cooperativa, es un conjunto acotado.
!!!def:Definición
Para un juego UNT canónico $(N, v)$ con $v$ verificando las propiedades anteriores, se define el **núcleo** como:
$$C_{UNT} =\{x\in v(N):\ \forall S\ \neg \exists y\in v(S)\ \forall i\in S\ (y_i>x_i)\}$$
Esta definición para los casos UNT también garantiza una gran coalición estable. La idea básica es que cualquier asignación de resultados en el núcleo de un juego UNT garantiza que ninguna coalición $S$ puede abandonar la gran coalición y proporcionar una asignación mejor para todos sus miembros. La diferencia con el caso UT es que, en el núcleo de la UNT, la estabilidad de la gran coalición se consigue sobre los elementos de los vectores de pagos, mientras que en el juego UT se consigue por la suma de esos elementos.
No siempre se puede garantizar la existencia de los núcleos para los juegos canónicos (UT o UNT). De hecho, en muchos juegos, el núcleo está vacío y, por tanto, la gran coalición no puede estabilizarse. En estos casos, se pueden utilizar conceptos de solución alternativos, como veremos más adelante. Sin embargo, la Teoría de Juegos de Coalición proporciona varias categorías de juegos que encajan en la definición que hemos dado de juegos canónicos y en los que se garantiza que el núcleo no es vacío.
Comencemos viendo un ejemplo en un juego canónico UT:
!!!Tip: Ejemplo
Consideremos un juego UT de voto mayoritario $(N, v)$ donde $N=\{1,2,3\}$. Los jugadores, por sí solos, no tienen poder de voto, por lo que $v(\{1\})=v(\{2\})=v(\{3\})=0$. Cualquier coalición de dos jugadores gana dos tercios del poder de voto, por lo que $v(\{1,2\})=v(\{1,3\})=v(\{2,3\})= 2/3$. La gran coalición gana todo el poder de voto, $v(\{1,2,3\})=1$. Claramente, este juego es superaditivo y está en forma característica.
Aplicando la definicion del núcleo para el caso UT obtenemos las siguientes desigualdades, y podemos deducir qué asignaciones estabilizan la gran coalición:
$$x_1 + x_2 + x_3 = v(\{1,2,3\})=1,\ x_1\geq 0,\ x_2\geq 0,\ x_3\geq 0$$
$$x_1 + x_2 \geq v(\{1,2\})=\frac{2}{3},\ x_1+x_3\geq v(\{1,3\})=\frac{2}{3},\ x_2+x_3\geq v(\{1,3\})=\frac{2}{3}$$
Manipulando estas desigualdades, se encuentra que el núcleo de este juego está formado por un único vector, $x=[\frac{1}{3},\frac{1}{3},\frac{1}{3}]$, que se corresponde con una división igualitaria de la utilidad total de la gran coalición entre los tres jugadores.
!!!
En general, dado un juego UT, $(N,v)$, y una imputación $x\in \mathbb{R}^n$, el núcleo se puede encontrar mediante la resolución de un problema lineal (LP) como el siguiente:
$$\{\arg\min_{x} \sum_{i\in N} x_i:\ \forall S\subseteq N\ (\sum_{i\in S} x_i\geq v(S))\}$$
En consecuencia, la existencia del núcleo del juego UT está relacionada con la viabilidad del LP anterior.
En general, calcular el núcleo a través de este LP es **NP**-completo [#Conitzer] debido a que el número de restricciones crece exponencialmente con el número de jugadores (algo que también es cierto para los juegos UNT), debido a que hay una restricción por cada subconjunto de $N$.
Pero existen varias técnicas disponibles para determinar si el núcleo no es vacío y encontrar algunas de sus asignaciones:
#### Método 1: Enfoque Gráfico
En los juegos con hasta 3 jugadores, la idea principal consiste en representar las restricciones anteriores en el plano $x_1+x_2+x_3=v(N)$, por lo que se puede identificar fácilmente la región que contiene la asignación del núcleo.
#### Método 2: Teorema de Bondareva-Shapley
Utilizando la **Teoría de la Dualidad**, existe una condición necesaria y suficiente para saber si el núcleo es no vacío a través del **Teorema de Bondareva-Shapley** para UT y UNT [#Shapley].
!!!def:Definición
Un juego UT está **equilibrado** si y sólo si se tiene $\sum_{S\subseteq N} \mu(S)v(S)\leq v(N)$ para todo $\mu$ peso equilibrado ($\mu:2^N\to [0,1]$ es equilibrado si $\sum_{S:i\in S} \mu(S)=1$ para todo $i\in N$).
Esta noción de juego equilibrado se puede interpretar como sigue:
!!!note:Juegos Equilibrados
Supongamos que cada jugador $i\in N$ posee una única unidad (de algún recurso, por ejemplo, tiempo), que puede ser distribuida entre todas las coaliciones de las que $i$ puede ser miembro. En este contexto, la condición $\sum_{S:i\in S} \mu(S)=1$ es simplemente una restricción de viabilidad en la asignación del recurso de los jugadores.
Supongamos que cada coalición $S\subseteq N$ está activa durante una fracción de tiempo $\mu(S)$, y si todos sus miembros están activos durante ese tiempo, esta coalición consigue una recompensa de $\mu(S)v(S)$.
El juego está equilibrado si no hay ninguna asignación de tiempo factible que pueda producir una recompensa total para los jugadores que supere el valor de la gran coalición $v(N)$.
Para los juegos canónicos UNT, existen dos definiciones diferentes de equilibrio (una de ellas es análoga al caso UT) que tienen en cuenta el hecho de que el valor $v$ en un juego UNT es un conjunto y no una función.
Para un juego canónico equilibrado UT se tiene el siguiente resultado:
!!!def: Teorema de Bondareva-Shapley
El núcleo de un juego es no vacío si y sólo si el juego es equilibrado.
Para juegos UNT, el teorema de Bondareva-Shapley también es cierto, sin embargo, en ese caso la condición de equilibrio presentada es suficiente pero no necesaria. En cualquier caso, en un juego canónico dado, siempre se puede demostrar que el núcleo es no vacío probando que el juego es equilibrado, tanto para juegos UT como para sus homólogos UNT.
#### Método 3: Juegos Convexos
Una subclase de juegos canónicos, llamados **convexos** siempre tienen núcleo no vacío.
!!!def:Definición
Un juego canónico UT es **convexo** si para todo $S_1,\ S_2\subseteq N$:
$$v(S_1) + v(S_2)\leq v(S_1\cup S_2) + v(S_1\cap S_2 )$$
!!!def:Definición
Alternativamente, un juego coalicional es **convexo** si:
$$v(S_1\cup \{i\})-v(S_1) \leq v(S_2\cup\{i\})-v(S_2),\ \forall S_1\subseteq S_2\subseteq N\setminus \{i\}$$
Esta definición alternativa implica que un juego es convexo si y sólo si para cada jugador $i\in N$ la contribución marginal de este jugador, es decir, la diferencia entre el valor de una coalición con y sin este jugador, no es decreciente con respecto a la relación de inclusión de conjuntos.
La propiedad de convexidad también puede extenderse a UNT de varias formas.
!!!def:Juegos Convexos
Si un juego es convexo, entonces es equilibrado y tiene núcleo no vacío.
!!!
Lo contrario no siempre es cierto.
Por ello, los juegos convexos constituyen una clase importante de juegos en los que el núcleo no es vacío.
#### Método 4: Juegos Simples
Para una subclase de juegos canónicos, llamados **simples**, existe una condición necesaria y suficiente para determinar que el núcleo no es vacío:
!!!def:Definición
Un **juego simple** es un juego de coalición en el que $v(S)\in \{0,1\}, \forall S\subseteq N$ y la gran coalición tiene $v(N)=1$.
Estos juegos modelan numerosos escenarios, especialmente los juegos de votación.
!!!def:Juegos con veto
Se sabe que un juego simple que contiene al menos un jugador de veto $i \in N$, es decir, un jugador $i$ tal que $v(N \setminus \{i\})=0$ tiene un núcleo no vacío.
Además, en este tipo de juegos simples, el núcleo está totalmente caracterizado, y consiste en todos los perfiles de pago no negativos $x \in \mathbb{R}^n$ tales que $x_i=0$ para cada jugador $i$ que no es un jugador de veto, y $\sum_{i\in N}x_i=v(N)=1$.
#### Método 5: Análisis de Imputaciones Concretas
Las técnicas anteriores se basan principalmente en propiedades teóricas de juegos, pero en muchos escenarios reales pueden ser necesarias técnicas alternativas para encontrar las asignaciones en el núcleo. Estas alternativas son inherentemente específicas de la aplicación y dependen de la naturaleza del juego definido.
En varias aplicaciones, basta con encontrar si las distribuciones de pago que interesan en el juego (por ejemplo, las distribuciones justas), se encuentran en el núcleo. En muchas aplicaciones (e incluso en entornos teóricos de juegos), el objetivo es evaluar si ciertos tipos bien definidos de asignaciones justas, como la justicia equitativa o la justicia proporcional, entre otras, están en el núcleo o no, sin encontrar todas las asignaciones que están en el núcleo. En este tipo de juegos, la demostración de que el núcleo no es vacío se realiza probando si estas asignaciones concretas se encuentran en el núcleo utilizando la definición explícita del núcleo (UT o UNT).
!!!Tip
Un ejemplo sencillo de esta técnica la vimos en el ejemplo anterior, donde comprobamos que la asignación equitativa se encontraba en el núcleo.
#### Método 6: Explotación de Características Específicas del Juego
En muchos juegos la explotación de características específicas del juego, como la definición matemática de su valor o la naturaleza y propiedades subyacentes del modelo de juego, ayuda a encontrar las imputaciones que se encuentran en el núcleo.
En muchos juegos canónicos, cuando las técnicas teóricas son demasiado complejas o difíciles de aplicar, se pueden explorar las propiedades del modelo de juego considerado.
## El valor de Shapley
A pesar de sus bondades, como concepto de solución el núcleo adolece de tres inconvenientes principales:
1. Puede estar vacío,
2. Puede ser bastante grande, por lo que la selección de una asignación adecuada del núcleo puede ser difícil, y
3. En muchos escenarios, las asignaciones que se encuentran en el núcleo pueden ser injustas para uno o más jugadores.
Estos inconvenientes motivaron la búsqueda de un concepto de solución que pudiera asociar a cada juego coalicional $(N,v)$ un único vector de pagos conocido como el **valor del juego** (que es bastante diferente del valor de una coalición). Shapley abordó este problema de forma axiomática definiendo un conjunto de propiedades deseables y caracterizó una aplicación única, $\phi(v)$, que satisface estos axiomas, conocido posteriormente como el **valor de Shapley**. Aunque originalmente el valor de Shapley se definió esencialmente para juegos UT, pronto se dieron extensiones para juegos UNT:
!!!def:Axiomas del Valor de Shapley
Shapley estableció cuatro axiomas como sigue ( $\phi_i$ es el pago dado al jugador $i$ por el valor de Shapley $\phi$):
1. **Eficiencia**: $\sum_{i\in N} \phi_i(v)=v(N)$.
2. **Simetría**: Si el jugador $i$ y el jugador $j$ verifican $v(S\cup\{i\})=v(S\cup\{j\})$ en cualquier coalición $S$ que no contenga al jugador $i$ y al jugador $j$, entonces $\phi_i(v)=\phi_j(v)$.
3. **Dummy**: Si el jugador $i$ verifica que $v(S\cup\{i\})=v(S)$ para toda coalición $S$ que no contenga a $i$, entonces $\phi_i(v)=0$.
4. **Aditividad**: Si $u$ y $v$ son funciones características, entonces $\phi(u+v)=\phi(v+u)=\phi(u)+\phi(v)$.
El axioma de eficiencia es, de hecho, el mismo que habíamos nombrado antes como la racionalidad de grupo. El axioma de simetría implica que, cuando dos jugadores tienen la misma contribución en una coalición, sus retribuciones asignadas deben ser iguales. El axioma de dummy no asigna ninguna retribución a los jugadores que no mejoran el valor de ninguna coalición. Por último, el axioma de aditividad vincula el valor de los diferentes juegos $u$ y $v$ y afirma que $\phi$ es un mapeo único sobre el espacio de todos los juegos de coalición.
!!!def: Teorema
Shapley demostró que existe una aplicación única, el **valor de Shapley**, $\phi$, sobre el espacio de todos los juegos coalicionales verificando los axiomas anteriores.
El valor de Shapley también tiene una interpretación alternativa que tiene en cuenta el orden en que los jugadores se unen a la gran coalición $N$: en el caso de que los jugadores se unan a la gran coalición en un orden aleatorio, el resultado asignado por el valor de Shapley a un jugador $i\in N$ es la contribución marginal esperada del jugador $i$ cuando se une a la gran coalición. La base de esta interpretación es que, dado cualquier juego canónico UT, $(N,v)$, para cada jugador $i\in N$ el valor Shapley $\phi(v)$ asigna la recompensa $\phi_i(v)$ dada por:
$$\phi_i(v)=\sum_{S\subseteq N\setminus\{i\}}\frac{|S|!(N - |S| - 1)!}{N!}(v(S\cup\{i\})-v(S))$$
donde se ve claramente que la contribución marginal de cada jugador $i$ en una coalición $S$ es $v(S\cup\{i\})-v(S)$. El peso que se utiliza delante de este término en cada sumando es la probabilidad de que el jugador $i$ se enfrente a la coalición $S$ al entrar en un ordenamiento aleatorio, es decir, que los jugadores que están delante de $i$ sean los que ya están en $S$. En este contexto, hay $|S|!$ maneras de posicionar a los jugadores de $S$ al principio de un ordenamiento, y $(N - |S| - 1)!$ maneras de posicionar a los jugadores restantes, excepto $i$, al final de un ordenamiento. La probabilidad de que se produzca un ordenamiento de este tipo (cuando todos los ordenamientos son igualmente probables) es, por tanto, $\frac{|S|!(N - |S| - 1)!}{N!}$, y, en consecuencia, el pago resultante $\phi_i(v)$ es la contribución marginal esperada, bajo el ordenamiento aleatorio de los jugadores para formar la gran coalición.
!!!
En general, el valor de Shapley no está relacionado con el núcleo. Sin embargo, en algunas aplicaciones, se puede demostrar que el valor de Shapley se encuentra en el núcleo.

Este resultado es interesante, ya que si se encuentra tal asignación, combina tanto la estabilidad del núcleo como los axiomas y la equidad del valor de Shapley. A este respecto, un resultado interesante de la teoría de juegos es que:
!!!def:Teorema
Para los juegos convexos el valor de Shapley se encuentra en el núcleo.
El valor de Shapley presenta un interesante concepto de solución para los juegos canónicos, y tiene numerosas aplicaciones en la teoría de juegos. Por ejemplo, en los juegos simples de votación coalicional, el valor de Shapley de un jugador representa su poder en el juego. En este tipo de juegos, el valor de Shapley se utiliza como índice de poder (conocido como **índice de Shapley-Shubik**), y tiene un gran número de aplicaciones en muchos entornos políticos y de teoría de juegos [#Owen]. En las redes de comunicación, el valor de Shapley presenta un criterio de equidad adecuado para asignar recursos o tasas de datos, como en [#La], [#Han] y [#Cai].
El cálculo del valor de Shapley se realiza generalmente utilizando la ecuación anterior, pero en juegos con un gran número de jugadores la complejidad computacional del valor de Shapley crece significativamente. Por ello, para calcular el valor de Shapley en un tiempo razonable, se han propuesto varias técnicas analíticas como extensiones multilineales [#Owen], y métodos de muestreo para juegos simples [#Castro].
## El Nucleolo
Otro concepto de solución interesante para los juegos canónicos es el **nucleolo**, que se introdujo principalmente para los juegos UT [#Owen] (y que será el que veremos aquí porque todavía no se ha formalizado una posible extensión del nucleolo para los juegos UNT).
La motivación básica del nucleolo es que, en lugar de aplicar una axiomatización general de la equidad para encontrar una asignación única de pagos, es decir, un valor para el juego, se puede proporcionar una asignación que minimice la insatisfacción de los jugadores con respecto a la asignación que pueden recibir en un juego dado.
!!!def: Definición
Para una coalición $S$, la **medida de insatisfacción** de una asignación $x\in \mathbb{R}^n$ se define como el **exceso**:
$$e(x, S)= v(S)-\sum_{j\in S} x_j$$
Claramente, una imputación, $x$, que pueda asegurar que todos los excesos (o insatisfacciones) se minimizan es de particular interés como solución y, por lo tanto, constituye la principal motivación detrás del concepto del nucleolo.
!!!def:Corolario
En particular, una imputación se encuentra en el núcleo de $(N, v)$ si y sólo si todos sus excesos son negativos o nulos.
!!!def:Definición
Se dice que un vector $y=(y_1,\dots,y_k)$ es lexicográficamente menor que un vector $z=(z_1, \dots, z_k)$, $y \le_{lex} z$, si: $$\exists\ i\leq k\ (y_i\le z_i \wedge \forall\ j\neq i\ (y_j= z_j))$$
!!!def:Definición: Nucleolo
Sea $O(x)$ el vector de todos los excesos en un juego canónico $(N,v)$, dispuestos en orden no creciente (excepto el exceso de la gran coalición $N$). Una imputación $x$ es un **nucleolo** si para cualquier otra imputación $z$, $O(x)\leq_{lex} O(z)$.
Por lo tanto, el nucleolo es la imputación que minimiza los excesos (insatisfacción) en un orden no creciente.
!!!def: Propiedades del Nucleolo
1. El nucleolo de un juego coalicional canónico existe y es único.
2. El nucleolo es grupal e individualmente racional (ya que es una imputación), y satisface los axiomas de simetría y de dummy de Shapley.
3. Si $C_{UT}\neq \emptyset$, entonces el nucleolo está en el núcleo.
4. El proceso para calcular el nucleolo es más complejo que el valor de Shapley:
1. En primer lugar, comenzamos por encontrar las imputaciones que distribuyen el valor de la gran coalición de tal manera que se minimice el exceso máximo (insatisfacción).
2. En el caso de que esta minimización tenga una solución única, esta solución es el nucleolo.
3. En caso contrario, se buscan las imputaciones que minimicen el segundo mayor exceso.
4. El procedimiento se repite para todos los excesos posteriores, hasta encontrar una solución única que sería el nucleolo. Estas minimizaciones secuenciales se resuelven mediante técnicas de programación lineal.

!!!Tip: Ejemplo
Las aplicaciones del nucleolo son numerosas en la teoría de juegos. Uno de los ejemplos más destacados es el **problema del contrato matrimonial** que apareció por primera vez en el [Talmud de Babilonia](https://es.wikipedia.org/wiki/Talmud_de_Babilonia) (300-500 d.C.):
Un hombre tiene tres esposas y se ha comprometido con un contrato matrimonial que especifica que deben recibir $100$, $200$ y $300$ unidades, respectivamente, después de su muerte. Esto implica que tras la muerte del hombre, este será el límite máximo que podrá reclamar cada una, pero en el contrato no dice cómo debe distribuirse en caso de que la cantidad no sea suficiente. Si este es el caso, el Talmud recomienda lo siguiente:
* Si tras de la muerte del hombre quedan $\alpha=100$, entonces cada esposa recibe $100/3$.
* Si tras de la muerte del hombre quedan $\alpha=200$, entonces la primera esposa obtiene $50$, y las otras dos $75$ cada una.
* Si tras de la muerte del hombre quedan $\alpha=300$, entonces la primera esposa obtiene $50$, la segunda esposa obtiene $100$, y la tercera $150$.
Obsérvese que el Talmud no especifica el reparto para otros valores de $\alpha$ pero si $\alpha\geq 600$ entonces cada esposa simplemente puede reclamar su derecho completo. Una pregunta clave que desconcertaba a los matemáticos e investigadores de la teoría de juegos era cómo se había calculado este reparto y resulta que el nucleolo es la respuesta. Modelemos el juego como un juego coalicional $(N,v)$ donde $N$ es el conjunto de las tres esposas que constituyen los jugadores y $v$ es el valor definido para cualquier coalición $S\subseteq N$ como $v(S)= \max(0, \alpha-\sum_{i\in N\setminus S} c_i)$, donde $c_i$ es la reclamación que la esposa $i$ debe obtener ($c_1=100$, $c_2=200$, $c_3=300$). Es fácil probar que, con esta formulación, los pagos recomendados por el Talmud coinciden con el nucleolo del juego. Este resultado pone de manifiesto la importancia del nucleolo a la hora de asignar retribuciones justas en un juego.
El nucleolo es un concepto interesante que combina una serie de criterios de equidad con la estabilidad, pero las aplicaciones que lo utilizan son todavía pocas debido, principalmente, a su complejidad computacional en algunos juegos. Sin embargo, con modelos adecuados, el nucleolo puede ser una solución óptima y justa para muchas aplicaciones.
## Aplicaciones a comunicaciones y redes
Los juegos canónicos de coalición cubren una amplia gama de aplicaciones de comunicación y redes y, de hecho, la mayoría de las actividades de investigación en estas áreas utilizan las herramientas que caen bajo la clase de juegos canónicos de coalición. Hay numerosas aplicaciones que utilizan modelos que implican juegos canónicos.
Un uso elegante e interesante de los juegos canónicos dentro de las redes de comunicación se presenta en [#La] para el estudio de la asignación de tasas en canales de acceso múltiple (MAC). El modelo que se muestra en ese trabajo aborda el problema de cómo asignar equitativamente las tasas de transmisión entre un número de usuarios que acceden a un canal MAC inalámbrico. En este modelo, los usuarios negocian para obtener una asignación justa de la tasa de transmisión total disponible. Cada usuario, o grupo de usuarios (coalición), que no obtiene una asignación justa de la tasa puede amenazar con actuar por su cuenta, lo que puede reducir la tasa disponible para el resto de usuarios. En consecuencia, el juego se modela como un juego coalicional.
En [#Mathur] se utilizan juegos canónicos para estudiar las posibilidades de cooperación entre receptores y transmisores de una sola antena en un canal de interferencia. El modelo considerado consiste en un conjunto de pares transmisor-receptor, en un canal de interferencia gaussiano. Los autores estudian la cooperación entre los receptores bajo dos modelos de juego coalicional: un modelo UT en el que los receptores se comunican a través de canales libres de ruido y decodifican conjuntamente las señales recibidas, y un modelo UNT en el que los receptores cooperan formando un detector lineal multiusuario (en este caso el canal de interferencia se reduce a un canal MAC). Además, los autores estudian el problema de cooperación de los transmisores bajo cooperación perfecta y cooperación parcial de decodificación y reenvío, considerando que los receptores han formado la gran coalición.
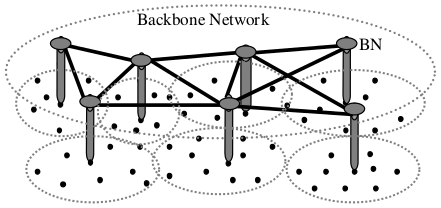
En [#Han] se usan juegos coalicionales canónicos para resolver un problema inherente a las redes ad hoc de reenvío de paquetes. En dichas redes, los usuarios que se encuentran en el centro de la red, conocidos como **nodos backbone**, tienen un beneficio mutuo para reenviar los paquetes de los demás. En cambio, los usuarios situados en el límite de la red, conocidos como **nodos límite**, no reciben ayuda de los nodos troncales, ya que éstos no necesitan la ayuda de los nodos límite en ningún momento. Por lo tanto, en esta situación, los nodos límite acaban por no tener forma de enviar sus paquetes a otros nodos (problema conocido como **la maldición de los nodos límite**). En el trabajo citado se propone un modelo de juego coalicional canónico entre un conjunto de jugadores que incluye todos los nodos límite y un único nodo troncal. En este modelo, formar una coalición, conlleva los siguientes beneficios:
* Al cooperar con un número de nodos límite y utilizar la transmisión cooperativa, el nodo troncal puede reducir su consumo de energía.
* A cambio, el nodo troncal se compromete a reenviar los paquetes de los nodos límite. Para la transmisión cooperativa, en una coalición, los nodos límite actúan como retransmisores mientras que el nodo troncal actúa como fuente.
En este juego, se demuestra que el núcleo no es vacío utilizando la propiedad de que cualquier grupo de nodos límite no recibe ninguna utilidad si se separa de la gran coalición con el nodo troncal (se clasificaría como una técnica siguiendo el método 6). Además, los autores estudian las condiciones bajo las cuales los conceptos de valor de Shapley y de nucleolo son adecuados para modelar el juego. Utilizando un juego canónico, la conectividad de la red ad hoc mejora significativamente.
Los juegos canónicos se han convertido en una herramienta importante para estudiar la cooperación y la equidad en las redes de comunicación, especialmente cuando la cooperación es siempre beneficiosa. Las aplicaciones futuras son numerosas, como el estudio de las ganancias de capacidad de transmisión cooperativa, la codificación cooperativa y distribuidad de fuentes, la retransmisión cooperativa en la radio cognitiva y muchas otras aplicaciones. En resumen, siempre que se conciba un esquema cooperativo que produzca ganancias significativas en cualquier capa, se pueden utilizar juegos coalicionales canónicos para evaluar la estabilidad de la gran coalición e identificar criterios de equidad en la asignación de las ganancias que resultan de la cooperación.
# Clase II: Formación de Coaliciones
Los **juegos de formación de coaliciones** abarcan los juegos de coalición en los que, a diferencia de la clase canónica, la estructura de las coaliciones y el coste de la cooperación desempeñan un papel importante.
En los juegos canónicos, así como en la mayor parte de la literatura, hay una suposición implícita de que formar una coalición es siempre beneficioso (por ejemplo, a través de la superaditividad). En muchos problemas, la formación de una coalición requiere un proceso de negociación o un proceso de intercambio de información que puede suponer un coste, reduciendo así las ganancias de la formación de la coalición.
!!!note:Características de Juegos de Formación de Coaliciones
Algunas de las principales características que hacen de un juego un juego de formación de coaliciones son las siguientes:
1. El juego está en forma característica o en forma de partición (UT o UNT) y, generalmente, no es superaditivo.
2. La formación de una coalición aporta beneficios a sus miembros, pero los beneficios están limitados por un coste de formación de la coalición, por lo que la gran coalición rara vez es la estructura óptima.
3. El objetivo es estudiar la estructura coalicional, es decir, responder a preguntas como: ¿qué coaliciones se formarán?, ¿cuál es el tamaño óptimo de la coalición?, y ¿cómo podemos evaluar las características de la estructura?.
4. El juego coalicional está sujeto a cambios en el entorno, como una variación en el número de jugadores, un cambio en la fuerza de cada jugador, u otros factores que pueden afectar a la topología de la red.
5. Una estructura coalicional es impuesta por un factor externo al juego (por ejemplo, restricciones físicas en el problema).
En general, los juegos de formación de coaliciones son de dos tipos: **estáticos** y **dinámicos**. En los primeros, se parte de una determinada estructura de coalición, y el objetivo es estudiar las propiedades de dicha estructura. El segundo es un marco más rico, donde los objetivos principales son analizar la formación de una estructura coalicional a través de la interacción de los jugadores y estudiar las propiedades de esta estructura y su adaptabilidad a las variaciones del entorno. A diferencia de los juegos canónicos, en los que existen reglas formales y conceptos analíticos, la resolución de un juego de formación de coaliciones es más difícil y puede depender de manera más explítica de la aplicación concreta en la que se ha definido.
Además, en los juegos canónicos, los conceptos de solución definidos (como el núcleo, el valor de Shapley y el nucleolo), suponían que la gran coalición se formaría debido a la superaditividad. Sin embargo, en [#Aumann] se pone de manifiesto por primera vez que la presencia de una estructura de coalición podría afectar a la definición y el uso de estos conceptos. Para ello, en un principio consideraron un juego coalicional UT y una estructura coalicional estática $\mathcal{B}= \{B_1, \dots, B_m\}$ (cada $B_i$ es una coalición) dada.
!!!def:Definición (Juegos de Formación)
Se define un **Juego de Formación de Coaliciones** como una tripleta $(N, v, \mathcal{B})$, donde $v$ es una función característica, donde:
* El concepto de racionalidad de grupo se sustituye por el de **eficiencia relativa**: Dado un vector de asignación, $x\in \mathbb{R}^n$, la eficiencia relativa implica que, para cada coalición $B_k \in \mathcal{B}$, $\sum_{i\in B_k}x_i=v(B_k)$. Por tanto, para cada coalición presente en $\mathcal{B}$, el valor total disponible para esa coalición se divide entre sus miembros, a diferencia de lo que ocurre en los juegos canónicos, donde es el valor de la gran coalición $v(N)$ el que se distribuye entre todos los jugadores.
* Se mantienen los axiomas de Shapley definidos anteriormente, excepto el axioma de eficiencia que se sustituye por un **axioma de eficiencia relativa**. Con este axioma modificado, el valor de Shapley de $(N,v,\mathcal{B})$ denominado $\mathcal{B}$-valor, tiene la **propiedad de restricción**, que implica que, para encontrar el $\mathcal{B}$-valor se pueden considerar los juegos coalicionales restringidos $\{(Bk, v|B_k): \ B_k\in \mathcal{B}\}$, donde $v|B_k$ es el valor del juego original $(N, v, \mathcal{B})$, definido sobre el conjunto de jugadores en $B_k$ (coalición). En consecuencia, para encontrar el $\mathcal{B}$-valor, procedemos en dos pasos, utilizando la propiedad de restricción:
1. Consideramos los juegos $\{(B_k, v|B_k)\}_k$ por separado y para cada uno de estos juegos encontramos el valor de Shapley utilizando la definición original.
2. El $\mathcal{B}$-valor del juego es el vector $\phi$ de pagos (de dimensión $1\times n$) construido combinando las asignaciones resultantes de cada juego restringido $(B_k, v|B_k)$.
* Las definiciones canónicas del núcleo y del nucleolo también se modifican, sustituyendo la racionalidad del grupo por la eficiencia relativa. Pero la propiedad de restricción no se aplica al núcleo ni al nucleolo, ya que éstos dependen de todas las coaliciones de $N$. Por tanto, en presencia de $\mathcal{B}$, el núcleo y el nucleolo dependen de los valores de las coaliciones $B_k \in \mathcal{B}$, así como de los valores de las coaliciones que no están en $\mathcal{B}$. Por lo tanto, el problema de encontrar el núcleo y el nucleolo de $(N, v,\mathcal{B})$ es más complejo que para el valor de Shapley.
Aunque esta aproximación se restringe a los juegos estáticos de formación de coaliciones con UT y en forma característica, ya se muestra que encontrar soluciones para los juegos de formación de coaliciones no es sencillo. La dificultad de dichas soluciones aumenta cuando se considera un juego UNT. Si además se añade la opción de un juego dinámico de formación de coaliciones habría que evaluar las asignaciones de pagos conjuntamente con la formación de la estructura de coalición, por lo que los conceptos de solución se vuelven aún más complejos de encontrar (aunque la propiedad de restricción del valor de Shapley facilita las cosas). Para ello, en los juegos de formación de coaliciones, especialmente la formación dinámica de coaliciones, se suelen redefinir los conceptos de solución o presentar alternativas específicas para el juego estudiado. Por tanto, a diferencia de los juegos canónicos en los que existen soluciones formales, la solución de un juego de formación de coaliciones depende del modelo y de los objetivos que se consideren.
La complejidad de estos casos excede nuestros objetivos en este curso, pero no queríamos al menos comentar su existencia y poder de relieve las diferencias.
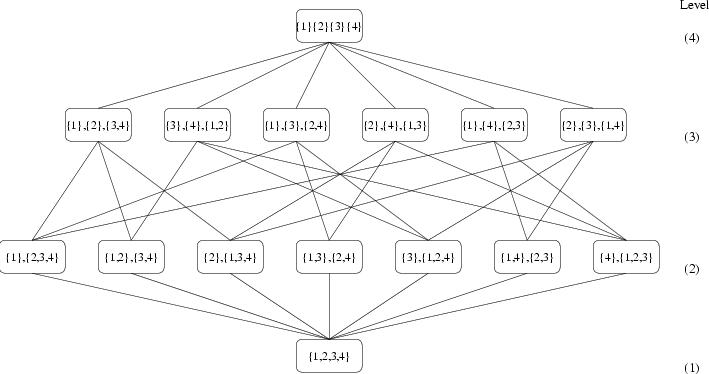
En muchas aplicaciones, la formación de coaliciones implica encontrar una estructura de coalición que maximice la utilidad total (bienestar social) si el juego es UT, o encontrar una estructura con una distribución de pagos óptima de Pareto para los jugadores si el juego es UNT. Para lograr este objetivo, se puede utilizar un enfoque centralizado; sin embargo, este enfoque es generalmente NP-completo. La razón es que encontrar una partición óptima requiere iterar sobre todas las particiones del conjunto de jugadores, y el número de particiones de un conjunto crece exponencialmente con su tamaño (número de jugadores) y viene dado por un valor conocido como el **número de Bell** (por ejemplo, para un juego en el que $N$ tiene sólo $10$ elementos, el número de particiones que debe realizar un enfoque centralizado es de $115.975$). Por lo tanto, encontrar una partición óptima a partir de un enfoque centralizado es, en general, computacionalmente complejo y poco práctico. En algunos casos, puede ser posible explorar las propiedades del juego, especialmente del valor $v$, para reducir la complejidad centralizada. No obstante, en muchas aplicaciones prácticas, es deseable que el proceso de formación de la coalición tenga lugar de forma distribuida, por lo que los jugadores tienen autonomía en la decisión de unirse o no a una coalición. De hecho, la complejidad del enfoque centralizado, así como la necesidad de soluciones distribuidas, han provocado un enorme crecimiento en la literatura de formación de coaliciones que tiene como objetivo encontrar algoritmos distribuidos y de baja complejidad para formar coaliciones.
Los enfoques utilizados para la formación de coaliciones distribuidas son muy variados y van desde enfoques heurísticos [#Sandholm], y métodos basados en cadenas de Markov [#Ray], hasta métodos basados en la teoría de conjuntos [#Apt], así como enfoques que utilizan la teoría de la negociación [#Arnold]. Aunque no existen reglas generales para la formación de coaliciones distribuidas, [#Apt] proporciona reglas genéricas que pueden utilizarse para derivar algoritmos de formación de coaliciones específicos para cada aplicación. Los tres ingredientes principales que se presentan en [27] son
* Órdenes bien definidos adecuados para comparar colecciones de coaliciones:
* El primer orden, conocido como el **orden utilitario**, establece que un grupo de jugadores prefiere organizarse en una colección $\mathcal{R}=\{R_1,\dots, R_k\}$ en lugar de $\mathcal{S}=\{S_1,\dots, S_m\}$, si el bienestar social total alcanzado en $\mathcal{R}$ es estrictamente mayor que en $\mathcal{S}$, es decir, $\sum_{i=1}^k v(R_i)> \sum_{i=1}^m v(S_i)$. Este orden suele ser adecuado para los juegos UT.
* Otro orden importante es el **orden de Pareto**, que basa la preferencia en los pagos individuales de los jugadores en lugar del valor de la coalición. Dadas dos asignaciones $x$ e $y$ que son asignadas por $\mathcal{R}$ y $\mathcal{S}$, respectivamente, a los mismos jugadores, $\mathcal{R}$ es preferida sobre $\mathcal{S}$ por el orden de Pareto si al menos un jugador mejora en $\mathcal{R}$ sin perjudicar a los otros jugadores, es decir, $x \geq y$ con al menos un elemento $x_i$ de $x$ tal que $x_i>y_i$. El orden de Pareto es adecuado tanto para juegos UT como UNT.
* Dos reglas sencillas para formar o romper coaliciones, denominadas **fusión** y **división**. Independientemente del orden seleccionado, se demuestra que cualquier secuencia arbitraria de estas dos reglas converge a una partición final de $N$:
* Dado un conjunto de jugadores $N$, cualquier colección de coaliciones disjuntas $\{S_1,\dots, S_m\}$, con $S_i\subseteq N$, puede acordar fusionarse en una única coalición $G=\cup_{i=1}^m S_i$, si esta nueva coalición $G$ es preferida por los jugadores sobre el estado anterior en función del orden de comparación seleccionado.
* Del mismo modo, una coalición $S$ se divide en coaliciones más pequeñas si el conjunto resultante $\{S_1,\dots, S_m\}$ es preferido por los jugadores sobre $S$.
* Nociones adecuadas para evaluar la estabilidad de una partición: como la **función de deserción**, que es una función que asocia a cada partición de la red, otra partición, un grupo de otras particiones, o un grupo de colecciones en $N$. Por medio de este tipo de funciones se puede evaluar si en una partición dada hay un incentivo para que los jugadores se desvíen y formen otras particiones o colecciones.
Los juegos de formación de coaliciones son diversos y no se limitan a este tipo de variantes. Por ejemplo, un tipo de juegos de formación de coaliciones, conocido como **juegos hedónicos de formación de coaliciones** [#Bogomonlaia], son bastante interesantes ya que permiten la formación de coaliciones (ya sean dinámicas o estáticas) basadas en las preferencias individuales de los jugadores. Además, estos juegos admiten diferentes conceptos de estabilidad que son extensiones de conceptos bien conocidos como el núcleo o el equilibrio de Nash utilizados en un entorno de formación de coaliciones. Por ello, los juegos hedónicos constituyen un marco analítico muy útil que tiene un gran potencial para ser adoptado, por ejemplo, en la modelización de problemas en redes inalámbricas y de comunicación. Además, más allá de los juegos de fusión y separación y de los juegos hedónicos, los juegos dinámicos de formación de coaliciones abarcan una multitud de algoritmos y conceptos.
## Juego del aeropuerto
Una aplicación clásica de los juegos cooperativos en problemas de asignación de costes es el juego del aeropuerto definido en [#Littlechild]. Las aeronaves que utilizan las instalaciones de un aeropuerto deben pagar por su uso y, en particular, deben pagar una tasa por cada operación en la que utilizan la pista de aterrizaje (es decir, por cada despegue y cada aterrizaje). En la mayoría de los casos, esos pagos tienen varias componentes, siendo una nada desdeñable la amortización del coste de construcción de la pista de aterrizaje a utilizar.
[#Littlechild] proponen modelizar el problema como un problema de asignación de costes y utilizar el valor de Shapley para resolver el cálculo de las tasas que corresponden a los costes de construcción.
De forma más precisa:
!!!
Sea $L = \{1, \dots , k\}$ el conjunto de los tipos distintos de aeronaves que utilizan el aeropuerto. El coste de construcción de una pista de aterrizaje que sea adecuada para su utilización por las aeronaves de tipo $j$ es $\alpha_j$ ($j\in L$). Asumimos, sin pérdida de generalidad, que $0 \leq \alpha_1\leq \dots \leq \alpha_k$. Denotamos $\alpha_0 = 0$, y por $g_j$ al conjunto de operaciones realizadas por las aeronaves de tipo $j$ ($n_j = |g_j|$) y $N$ es el conjunto de todas las operaciones, es decir, $N = \cup_{j\in L} g_l$. Para un subconjunto $S \subseteq N$, denotamos por $t(S)$ el mayor de los tipos involucrados en las operaciones en $S$:
$$t(S) = \max\{j\in L :\ S \cap g_l\neq \emptyset\}$$
A continuación, definimos el coste asociado a $S$, $c(S) = \alpha_{t(S)}$ (obsérvese que $c$ satisface una propiedad de monotonía). Por tanto, tenemos definido un problema de asignación de costes $(N, c)$ en el cual $c(N) = \alpha_k$ debe ser repartido entre las operaciones de las aeronaves, es decir, las tasas a pagar deben garantizar la amortización de $\alpha_k$.
El problema de asignación de costes que acabamos de definir se llama **juego del aeropuerto**. Obsérvese que los jugadores de un juego del aeropuerto son las operaciones de despegue y aterrizaje realizadas por las aeronaves, y no las aeronaves mismas. De ahora en adelante hablaremos de jugadores en lugar de operaciones.
Lo habitual es que los juegos del aeropuerto tengan muchos jugadores, por lo que es muy importante utilizar reglas de asignación que tengan buenas propiedades computacionales. En general, el valor de Shapley es de cálculo complejo, pero en Littlechild y Owen (1973) se obtiene la siguiente expresión para su cálculo en este contexto. Esta expresión destaca por su simplicidad y rapidez de cálculo.
!!!def: Teorema
Sea $(N, c)$ un juego del aeropuerto. Entonces, el valor de Shapley de $(N, c)$ puede calcularse, para cada $i \in N$, como
$$\phi_i(N, c) = \sum_{j=1}^{t(i)}\frac{\alpha_j − \alpha_{j-1}}{u_j}$$
donde $\alpha_0 = 0$, $t(i)$ es el tipo de aeronave del jugador $i$, y $u_j$ es el número de jugadores de tipo mayor o igual que $j$.
Este reparto tiene la siguiente interpretación:
* El coste, $\alpha_1$, de construcción de la parte de la pista de aterrizaje que necesitan todos los tipos de aeronave se divide a partes iguales entre todos los jugadores.
* El coste incremental, $\alpha_2−\alpha_1$, necesario para todas las aeronaves a excepción de las del primer tipo, se divide a partes iguales entre todos los jugadores de tipos $\{2, 3,\dots, k\}$.
* Y así sucesivamente...
Además de por sus propiedades computacionales, el valor de Shapley es un regla de asignación especialmente apropiada para los juegos del aeropuerto por ser estos convexos, y en consecuencia el valor de Shapley de un juego del aeropuerto siempre pertenece al núcleo.
Las estructuras coalicionales surgen de un modo particularmente natural en los juegos del aeropuerto, debido a que las aeronaves pertenecen a compañías aéreas. Y este es un hecho que debe ser tenido en cuenta a la hora de hacer los repartos de los costes. Según [#Vázquez-Brage]:
> *Aunque el modelo del juego del aeropuerto estudiado hasta ahora en la literatura ha sido bastante valioso,
> creemos que hay un aspecto importante de la determinación de las tasas de aterrizaje de los aviones que se
> ignora, a saber, el hecho de que los aviones están organizados en aerolíneas. Sostenemos que los aviones no
> deben considerarse como unidades aisladas, sino como parte de una compañía aérea, y que las compañías más
> grandes tienen más posibilidades de negociar descuentos u otras ventajas de costes que las más pequeñas.*
Por ello, estos autores modelizan este problema con una estructura coalicional que viene dada por las compañías aéreas: $P_a\in P$ es la clase de todas las operaciones en $N$ llevadas a cabo por aeronaves pertenecientes a la compañía aérea $a\in M$, donde $M$ es el conjunto de las compañías aéreas que utilizan el aeropuerto.
## Aplicaciones
Las aplicaciones potenciales de los juegos de formación de coaliciones en las redes de comunicación son numerosas y diversas. Además de casuísticas similares a la clase anterior, ya se han aplicado para mejorar la seguridad de la capa física de los nodos inalámbricos mediante la cooperación entre los transmisores, o para la formación de coaliciones entre una serie de agentes autónomos, como los vehículos aéreos no tripulados, en el contexto de la recogida y transmisión de datos en redes inalámbricas.
Por otra parte, recientemente ha aumentado el interés por el diseño de sistemas de comunicación autónomos. Los sistemas autónomos son redes que se autoconfiguran, se autoorganizan, se autooptimizan y se autoprotegen. En este tipo de redes, los usuarios deben ser capaces de aprender y adaptarse a su entorno (cambios en la topología, las tecnologías, las demandas de servicio, el contexto de la aplicación, etc.), proporcionando así la tan necesaria flexibilidad y escalabilidad funcional. Por ello, las aplicaciones potenciales de los juegos de formación de coaliciones abarcan las redes cooperativas, las redes de sensores inalámbricos, las redes de próxima generación del protocolo IP, las redes ad hoc autoconfigurables y muchas otras. En general, siempre que se necesiten algoritmos distribuidos para redes autonómicas, la formación de coaliciones es una herramienta sólida para modelar tales problemas. Asimismo, cualquier problema que implique el estudio del comportamiento de los nodos inalámbricos cooperativos cuando existe un coste es candidato a ser modelado mediante juegos de formación de coaliciones.
# Clase III: Grafos de Coaliciones
En los juegos canónicos y de formación de coaliciones, la utilidad o el valor de una coalición no depende de cómo están interconectados los jugadores dentro de la coalición. Sin embargo, se ha demostrado que, en ciertos escenarios, la estructura de comunicación subyacente entre los jugadores de un juego coalicional puede tener un gran impacto en la utilidad y otras características del juego. Por estructura de comunicación subyacente entendemos el grafo que representa la conectividad de los jugadores entre sí, es decir, qué jugador se comunica con cuál dentro de cada coalición.
!!!note:Características de Juegos de Grafos
En general, las principales propiedades que distinguen a un juego de grafo coalicional son las siguientes:
1. El juego coalicional tiene forma de grafo, y puede ser UT o UNT. Sin embargo, el valor de una coalición puede depender de la estructura externa de la red, como hemos comentado anteriormente.
2. La interconexión entre los jugadores de cada coalición, es decir, quién está conectado con quién, influye mucho en las características y el resultado del juego.
3. El objetivo principal es derivar algoritmos distribuidos de baja complejidad para los jugadores que desean construir un grafo de red (dirigido o no dirigido) y no sólo grupos de coalición como en los juegos de formación de coaliciones. Otro objetivo es estudiar las propiedades (estabilidad, eficiencia, etc.) del grafo formado.
La idea de tener un valor dependiente de un grafo de comunicación entre los jugadores fue introducida por primera vez por Myerson en [#Myerson2] a través de la función de grafo para juegos TU. En este trabajo, partiendo de un juego coalicional canónico UT, $(N, v)$, y dado un grafo no dirigido $G$ que interconecta a los jugadores en el juego, Myerson intenta encontrar una solución justa. Para ello, se define una nueva función de valor, $u$, que depende del grafo. Para evaluar el valor $u$ de una coalición $S$, ésta se divide en coaliciones más pequeñas en función de los jugadores que están conectados a través de $G$. Por ejemplo, dada una coalición de tres jugadores $S=\{1, 2, 3\}$ y un grafo $G=\{(2, 3)\}$ (sólo los jugadores $2$ y $3$ están conectados por un enlace en $G$), el valor $u(S, G)= v(\{2,3\})+v(\{1\})$, donde $v$ es el valor original del juego canónico. Usando el nuevo valor $u$, Myerson presenta un enfoque axiomático, similar al valor de Shapley, para resolver el juego en forma de función de grafo. Myerson muestra que una solución justa del juego canónico $(N, v)$ en presencia de una estructura de grafo es el valor de Shapley del juego $(N, u)$. Esta solución se conoce como el **valor Myerson**. El inconveniente de este enfoque es que el valor $u$ de una coalición sólo depende de los jugadores conectados en la coalición sin depender de la estructura, por ejemplo, para el ejemplo visto al inicio del capítulo, para ambos grafos $G_S^1$ y $G_S^2$ los valores $u$ son iguales (aunque los pagos recibidos por los jugadores en $G_S^1$ y $G_S^2$ a través de la asignación del valor Myerson serían diferentes debido a los diferentes gráficos).
No obstante, el trabajo de Myerson generó otros trabajos, y en [#Jackson] se amplió el valor para que dependiera de la estructura del grafo, y no sólo de los componentes conectados. Al hacerlo, los juegos de grafos coalicionales se convirtieron en un marco más rico, aunque la búsqueda de soluciones se hizo más compleja. Mientras que en [#Myerson2] el objetivo era encontrar una solución, las nuevas aproximaciones buscaban algoritmos para formar el grafo. Una herramienta destacada en este ámbito es la teoría de juegos no cooperativos (principalmente, los juegos en forma no extensiva), que se ha utilizado para formar el grafo de la red. A pesar de que este enfoque es poco práctico en muchas situaciones, ya que requiere enumerar todos los enlaces posibles en el grafo, lo cual es un problema combinatorio complejo, con él empezó a aparecer una nueva clase de juegos, que se conocen como **juegos de formación de redes**, cuyo objetivo es estudiar las interacciones entre un grupo de jugadores que desean formar un grafo.
Para la formación del grafo existe una amplia gama de enfoques que se agrupan en dos tipos: **miope** y **clarividente** (o dinámicos). La principal diferencia entre estos dos tipos es que, en los enfoques miopes los jugadores juegan sus estrategias teniendo en cuenta el estado actual de la red, mientras que en los algoritmos clarividentes los jugadores adaptan su estrategia aprendiendo y prediciendo las estrategias futuras de los demás jugadores. Para ambos enfoques se pueden utilizar conceptos conocidos de la teoría de los juegos no cooperativos. El más popular de estos enfoques es considerar la formación de la red como un juego no cooperativo de suma no nula, en el que las estrategias de los jugadores consisten en seleccionar uno o más enlaces para formar o romper. En este caso, la estrategia de cada juagador consiste en elegir el enlace o enlaces a formar o romper, maximizando su utilidad. Bajo ciertas condiciones sobre las utilidades, la dinámica de mejor respuesta converge a un equilibrio de Nash, que constituye una **red de Nash**. El principal inconveniente de buscar una red de Nash es que, en muchos juegos de formación de redes, estas redes son grafos triviales (como el grafo vacío) o pueden ser ineficientes. Por estas razones, se ha desarrollado un nuevo tipo de juegos de formación de redes que utiliza nuevos conceptos de estabilidad, como la **estabilidad por pares** y la **estabilidad coalicional**. La idea básica es presentar nociones de estabilidad que dependen de las desviaciones de un grupo de jugadores en lugar de las desviaciones unilaterales permitidas por el equilibrio de Nash.
Independientemente del concepto de estabilidad, una cuestión de diseño clave en los juegos de formación de redes es el equilibrio entre la estabilidad y la eficiencia. Es deseable idear algoritmos para formar redes estables que también puedan ser eficientes en términos de distribución de resultados o bienestar social total. Existen varios enfoques para idear tales algoritmos, en particular utilizando procesos estocásticos, técnicas de teoría de grafos o juegos no cooperativos [#Jackson2].
Por último, tambien se pueden proponer otros enfoques que están estrechamente ligados a los juegos canónicos. Por ejemplo, en [#Herings] se propone formular un modelo similar a un juego canónico para un juego UNT, en el que se tiene en cuenta la estructura del grafo. Se propone una extensión del núcleo denominada **núcleo equilibrado** que tiene en cuenta la estructura del grafo, y para el que, bajo ciertas condiciones, análogas a las condiciones de equilibrio de los juegos canónicos, se muestra que este núcleo equilibrado no es vacío.
## Aplicaciones
La presencia de un grafo de red es omnipresente en muchas aplicaciones inalámbricas y de comunicación. Para diseñar, comprender y analizar dichos grafos, los juegos de grafos coalicionales son la herramienta precisa. A través de los distintos conceptos relativos a la formación de redes, la estabilidad, la equidad u otros, se pueden modelar diversos problemas. Por ejemplo, los juegos de formación de redes han sido ampliamente utilizados en problemas de enrutamiento, donde cada nodo tiene como objetivo minimizar su función de coste, que refleja los distintos costes en los que puede incurrir el tráfico de enrutamiento (coste de enrutamiento, coste de mantenimiento de enlaces, coste de desconexión, etc.). Además, el uso de juegos de formación de redes en aplicaciones de enrutamiento no se limita únicamente a la formación de la red, sino también al estudio de las propiedades de una red existente.
Pero las aplicaciones de los juegos de grafos coalicionales no se limitan en absoluto a los problemas de enrutamiento. Por ejemplo, son herramientas adecuadas para analizar problemas relacionados con la gestión de la confianza en la información entre pares (por ejemplo, en redes inalámbricas), la radio cognitiva (un paradigma de la comunicación inalámbrica en la cual tanto las redes como los mismos nodos inalámbricos cambian los parámetros particulares de transmisión o de recepción para ejecutar su cometido de forma eficiente sin interferir con los usuarios autorizados; esta alteración de parámetros está basada en la observación de varios factores del entorno interno y externo de la radio cognitiva, tales como el espectro de radiofrecuencia, el comportamiento del usuario o el estado de la red), la selección de relevos en las comunicaciones cooperativas, la detección de intrusiones, la transferencia de datos entre pares, la retransmisión multisalto, el reenvío de paquetes en las redes de sensores y muchos otros.
# Referencias
[#Apt]: K. Apt and A. Witzel, *A generic approach to coalition formation*, Proc. Int. Workshop Computational Social Choice (COMSOC), Amsterdam, The Netherlands, Dec. 2006.
[#Arnold]: T. Arnold and U. Schwalbe, *Dynamic coalition formation and the core*, J. Econ. Behavior Org., vol. 49, pp. 363–380, Nov. 2002.
[#Aumann]: R. J. Aumann and B. Peleg, *Von neumann-morgenstern solutions to cooperative games without side payments*, Bull. Amer. Math. Soc., vol. 6, no. 3, pp. 173–179, 1960.
[#Aumann]: R. Aumann and J. Drèze, *Cooperative games with coalition structures*, Int. J. Game Theory, vol. 3, pp. 317–237, Dec. 1974.
[#Bogomonlaia]: A. Bogomonlaia and M. Jackson, *The stability of hedonic coalition structures*, Games Econ. Behavior, vol. 38, pp. 201–230, Jan. 2002.
[#Cai]: J. Cai and U. Pooch, *Allocate fair payoff for cooperation in wireless ad hoc networks using shapley value*, in Proc. Int. Parallel and Distributed Processing Symp., Santa Fe, NM, Apr. 2004, pp. 219–227.
[#Castro]: J. Castro, D. Gomez, and J. Tejada, *Polynomial calculation of the shapley value based on sampling*, Comput. Oper. Res., vol. 36, pp. 1726–1730, May 2009.
[#Conitzer]: V. Conitzer and T. Sandholm, *Complexity of determining nonemptiness of the core*, in Proc. 18th Joint Conf. Artifical Intelligence, Acapulco, Mexico, Aug. 2003.
[#Han]: Z. Han and V. Poor, *Coalition games with cooperative transmission: A cure for the curse of boundary nodes in selfish packet-forwarding wireless networks*, IEEE Trans. Commun., vol. 57, pp. 203–213, Jan. 2009.
[#Herings]: P. Herings, G. van der Laan, and D. Talman, *Cooperative games in graph structure*, Res. Memoranda, Maastricht Res. Sch. Econ., Technol., Org., Memo. Maastricht, The Netherlands, no. 11, Aug. 2002.
[#Jackson]: M. Jackson and A. Wolinsky, *A strategic model of social and economic networks*, J. Econ. Theory, vol. 71, no. 1, pp. 44–74, 1996.
[#Jackson2]: M. O. Jackson, *A survey of models of network formation: Stability and efficiency*, California Inst. Technol., Div. Humanities Social Sci., CA, Rep. 1161, Nov. 2003.
[#La]: R. La and V. Anantharam, *A game-theoretic look at the Gaussian multiaccess channel*, DIMACS Series in Discrete Math. Theoretical Comp. Sci., vol. 66, pp. 87–106.
[#Littlechild]: SC. Littlechild, G. Owen (1973). A simple expression for the Shapley value in a special case, Management Science 20, 370–372.
[#Mathur]: S. Mathur, L. Sankaranarayanan, and N. Mandayam, *Coalitions in cooperative wireless networks*, IEEE J. Select. Areas Commun., vol. 26, pp. 1104–1115, Sept. 2008.
[#Myerson]: R. B. Myerson, Game Theory, Analysis of Conflict. Cambridge, MA: Harvard Univ. Press, Sept. 1991.
[#Myerson2]: R. Myerson, *Graphs and cooperation in games*, Math. Oper. Res., vol. 2, pp. 225–229, June 1977.
[#Neumann]: J. von Neumann and O. Morgenstern, Theory of Games and Economic Behavior. Princeton, NJ: Princeton Univ. Press, Sept. 1944.
[#Owen]: G. Owen, Game Theory, 3rd ed. London, U.K.: Academic, Oct. 1995.
[#Ray]: D. Ray, A Game-Theoretic Perspective on Coalition Formation. New York: Oxford Univ. Press, Jan. 2007.
[#Saad]: W. Saad, Z. Han, M. Debbah, A. Hjorungnes, T. Basar, *Coalitional game theory for communication networks*, in IEEE Signal Processing Magazine, vol. 26, no. 5, pp. 77-97, September 2009.
[#Sandholm]: T. Sandholm, K. Larson, M. Anderson, O. Shehory, and F. Tohme, *Coalition structure generation with worst case guarantees*, Artifi. Intell., vol. 10, pp. 209–238, July 1999.
[#Shapley]: L. Shapley and M. Shubik, *The assignment game i: The core*, Int. J. Game
Theory, vol. 1, no. 1, pp. 111–130, 1972.
[#Thrall]: R. Thrall and W. Lucas, *N-person games in partition function form*, Naval Res. Logistics Quart., vol. 10, no. 1, pp. 281–298, 1963.
[#Vázquez-Brage]: Vázquez-Brage M, van den Nouweland A, García-Jurado I (1997). Owen’s coalitional value and aircraft landing fees, Mathematical Social Sciences 34, 273–286.