**SVRAI** DEEP Q-LEARNING MULTIAGENTE Roldan Rojo, Adrian El objetivo de este documento es dar una introducción al deep q-learning multiagente de forma que uno sea capaz de entender los conceptos básicos de este y ser capaz de llevarlos a un entorno de programación, así como entender de manera general como se realiza el aprendizaje por refuerzo que es el tipo de aprendizaje utilizado para el deep q-learning. Lo primero que vamos a ver son conceptos fundamentales pare entender este tema, como son los procesos de decisión de Márkov y q learning. Luego de esto veremos como introducir redes neuronales en el algoritmo de q-learning para así dar lugar al deep q-learning. Por último, veremos cómo se adapta estos algoritmos a un sistema multiagente. Conceptos básicos ============================================================== Procesos de decisión de Márkov (MDP) --------------------------------------------------------------- Lo primero que tenemos que entender de este tema son los procesos de decisión de Márkov, que son la piedra angular del aprendizaje por refuerzo. Los MDP se utilizar para describir formalmente el entorno donde se desarrolla el aprendizaje por refuerzo, de forma que nosotros podamos definir uno estados en donde se encuentra un agente, para que este pueda llevar a cavo ciertas acciones que puedan dar lugar a un nuevo estado. El objetivo de los MDP es maximizar una función de recompensa de forma que si S es el conjunto de estados donde puede encontrarse un agente la función de recompensa seria de la siguiente forma: $$ r: S \rightarrow R $$ Siendo R la recompensa obtenida tras realizar cierta acción en un estado s. El proceso por el cual un agente pasa de un estado a otro mediante una acción es definido por una función de transición T(s, a, s’) siendo s el estado inicial, a la acción realizada y s’ el estado alcanzado al realizar la acción a. Esta función da como resultado la probabilidad que tiene el agente de alcanzar s’ al realizar la acción a. Puede darse el caso de que tras realizar la acción a vuelva al mismo estado del que partí, en este caso nos encontraríamos en un mundo no determinista.  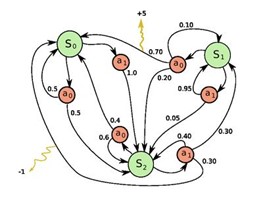Si el objetivo de los MDP es maximizar la función de recompensa entonces el objetivo del agente en cuestión será encontrar una política optima que maximice su recompensa, entendiendo política como el comportamiento que tiene el agente en cada uno de los estados, esta política la denotaremos como π. Por lo tanto, la política optima se puede definir como: $$ \pi^{*} (s) = arg max \sum_{s'}^{}T(s,a,s')u(s')$$ Donde u(s’) es la utilidad real que tiene un agente por estar en el estado s. Esta utilidad se define con la ecuación de Bellman que se utiliza principalmente para no solo tener en cuenta la recompensa inmediatamente dada, sino además su recompensa futura. $$ \begin{equation} \label{ecuacion-Bellman} u(s) = r(s) + \gamma \cdot \max_a \sum_{s'} T(s,a,s')u(s') \end{equation} $$ Siendo r(s) la recompensa inmediata obtenida por estar en el estado s, γ el factor de descuento que reduce el peso que tengan las recompensas futuras a comparación de las inmediatas y el sumatorio representaría la máxima recompensa que puedo obtener al realizar cualquier acción en el estado s. Q Learning --------------------------------------------------------------- Una vez hayamos entendido los conceptos básicos de los MDP podemos pasar a uno de los métodos de resolución de estos procesos más famosos el q learning. Q-learning es un método de aprendizaje por refuerzo que se basa en aprender una función Q. Esta función Q lo que me indica es que basado en el estado en el que estoy y una cierta acción que voy a tomar cual será la recompensa que obtendré y que podría obtener en un futuro, es parecido a la ecuación de Bellman que vimos anteriormente: $$ Q^{*} (s_{t},a_{t}) =r_{t+1} + \gamma * maxQ^{*}(s_{t+1},a) $$ Donde $ r_{t+1} $ es la recompensa inmediata al alcanzar el nuevo estado, γ es el factor de descuento de recompensa futura y $ maxQ^* (s_{t+1},a) $ es la máxima recompensa obtenible del estado $ s_{t+1} $ al realizar cualquier acción. Esta información se almacena en una tabla de forma que una vez entrenado el algoritmo pueda encontrar la política más optima que puede tomar el agente para maximizar la recompensa. Por lo tanto, yo tendría un agente el cual se mueve por el mundo, para cada estado y acción tomados almaceno su valor de Q en una tabla, de forma que pueda actualizar ese valor cada vez que vuelva a tomar esa misma acción en ese mismo estado por lo que el valor de Q almacenado vendría a ser: $$ Q (s_{t},a_{t}) \leftarrow Q (s_{t},a_{t}) + \alpha(s_{t+1} * \gamma * maxQ^{*}(s_{t+1},a) - Q (s_{t},a_{t}) ) $$ Para hacerlo más sencillo la interpretación de esta ecuación seria que en la tabla almaceno el valor de Q de una acción en un determinado estado y esta Q viene dada por el valor que ya tenía anteriormente en la tabla más el valor de recompensa obtenido actualmente (esto seria la recompensa inmediata mas la fututa) multiplicado por un índice de aprendizaje α. Este índice de aprendizaje lo que hace es determinar hasta que punto la nueva información obtenida va a sobrescribir a la vieja, 0 seria para no sobrescribir nada y 1 para que solo cuente la nueva información.  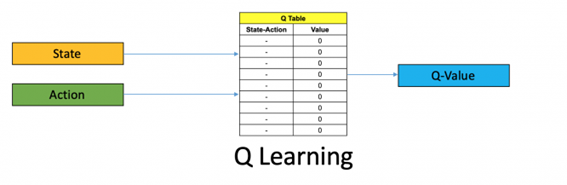Con todo lo explicado ya podemos construir nuestro algoritmo de Q-learning que seria de la siguiente forma: !!!def:Algoritmo Q-learning 1. Inicio la tabla con valores de Q(s,a) aleatorios o a 0 2. Iniciamos el entorno partiendo de un estado s - Elegimos una acción y la realizamos - Obtenemos r y el nuevo estado s’ - En la tabla actualizamos el valor de Q mediante la ecuación anterior - Repetimos hasta llegar al estado final 3. Volvemos al paso 2 las veces que hayamos determinado en el algoritmo Este seria el algoritmo de Q-learning, en el siguiente apartado veremos como adaptarlo para obtener el algoritmo del deep q-learning Deep q learning ============================================================== Deep q-learning es una adaptación del algoritmo de q-learning en el cual sustituimos la tabla donde almacenábamos las Q por una red neuronal que nos devuelva el valor de Q para cada acción. Pero antes de entrar en detalle veamos que son las redes neuronales un poco por encima. Redes neuronales artificiales -------------------------------------------------------------- Las redes neurales artificiales son modelos de inteligencia artificial inspirados en el funcionamiento del cerebro humano, en ellas varias capas de neuronas interconectadas reciben información y envían dicha información a otras neuronas, gracias a esta estructura podemos resolver problemas que a priori no podríamos resolver mediante programación lógica. La red neuronal está formada por una capa de entrada, una o varias capas ocultas y una capa de salida, la capa de entrada recibe la información y la envía a las capas ocultas que posteriormente enviaran la información a la capa de salida.  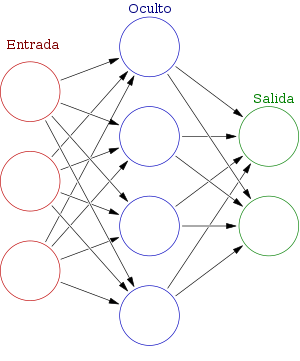Cada neurona está conectada con otras mediante un enlace, estos enlaces llevan la información de una neurona a otra multiplicando dicha información por un peso. Este peso se encarga de incrementar o inhibir la información que sale de una neurona y cada neurona posee una función de activación a su salida mediante la cual modifica la información que le llega, esta función puede ser establecida por el programador y existen diversas funciones como por ejemplo la sigmoidal o la ReLu.  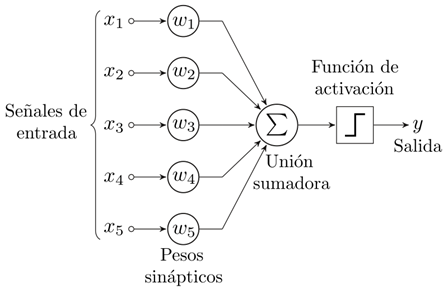La red neuronal es entrenada ajustando cada uno de los pesos de todas las neuronas, para así hallar la mejor aproximación a la solución posible. 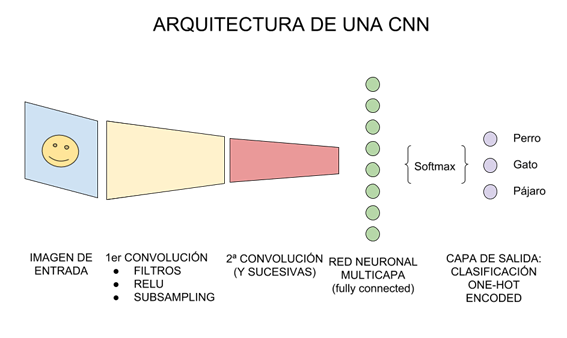El tipo de red neuronal que mas se suele utilizar para deep q learning son las redes neuronales convolucionales que se encargan de procesar imagenes, debido a que los estados de nuestro problema suelen ser la visión que tenemos nosotros de este, por ejemplo, si quiero realizar deep q learning a un juego como pacman mis estados pueden ser la pantalla de juego donde aparecen todos los elementos de este. Las redes neuronales convolucionales (CNN) son redes neuronales a las que se les ha añadido una o varias capas de convolución delante. Este tipo de redes está diseñado para trabajar, sobre todo, con imágenes. La convolución consiste en tomar un grupo de pixeles y realizar su producto escalar mediante un kernel, el kernel es una especie de filtro el cual se dedica a resaltar patrones importantes de la imagen. Si es una imagen a color se utilizarán 3 kernels para cada uno de ellos, rojo, verde y azul.  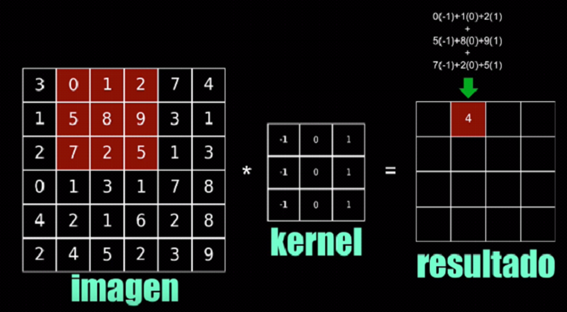Al aplicar varios kernels a la imagen obtendremos varias de un tamaño menor por lo que a medida que valla avanzando el proceso de convolución obtendremos una mayor cantidad de imágenes, pero de menor tamaño. Cada imagen, al utilizar distintos kernels, resaltara un aspecto de la imagen original. Una vez realizada la convolución utilizaremos el valor de cada píxel resultante de cada imagen como entrada para la red neuronal, si es una imagen a color cada píxel representara 3 entradas, una para cada color. El valor del píxel debe estar normalizado entre 0 y 1 por lo que si el valor para cada color está comprendido entre 0 y 255 habría que dividir este valor entre 0 y 255 para normalizar estos datos.  El “deep” de q-learning -------------------------------------------------------------- Una vez que hemos entendido como funciona una red neuronal pasaremos a ver como se incorpora está dentro de q-learning. Una de las desventajas de q-learning es que a medida que el problema se hace más grande también aumenta el numero de estados y acciones por lo que el problema podría llegar a ser inabordable, por ejemplo, en el ajedrez tendré un estado por cada una de las posibles jugadas que existen, esto hace un numero de estados demasiado grande como para poder ser almacenado en una tabla. Por este motivo deep q-learning es una alternativa mucho mas atractiva ya que lo único que almacenamos es la red neuronal y es esta la encargada de decidir cual será la mejor acción posible. El fundamento básico de deep q-learning es utilizar una red neuronal que aproxime la función Q, recordemos que esta función tenía la siguiente forma: $$ Q^{*} (s_{t},a_{t}) =r_{t+1} + \gamma * maxQ^{*}(s_{t+1},a) $$ Por tanto, es de esperar que la salida de nuestra red sea el valor de Q, sin embargo, esto no es del todo correcto, por que lo que realmente obtengo de la salida es el valor Q asociado a cada acción disponible, es decir, si tengo 4 posibles acciones la red neuronal tendrá como salida 4 valores de Q asociados a cada una de ellas, por tanto, la mejor acción posible será la que mayor valor de Q tenga. Esto es debido a que en lugar de recibir como entrada el estado y la acción como se hacía en q-learning ahora la entrada es únicamente el estado actual. Esto lo podemos ver con mayor claridad en la siguiente imagen:  Hasta este momento el concepto de deep q-learning es simple, sin embargo, hay algo en lo que es del todo cierto y es que en realidad deep q-learning utiliza dos redes neuronales, una de ellas es la red neuronal principal (main Neural Network) que representaremos como θ y otra es la red neuronal objetivo (target Neural Network) que representaremos como θ'. La red neuronal principal es la red que se encarga de estimar los valores de q para el estado actual, además de ser la que utilizamos para elegir las acciones y la red objetivo es la que se encarga de calcular los valores de Q del próximo estado. La red principal es la red que se entrena, mientras que la red objetivo tiene los pesos congelados la mayoría del tiempo y tras varias iteraciones los pesos de la red principal son copiados a la red objetivo. Este uso de dos redes se utiliza para añadir estabilidad en el entrenamiento. Por tanto, si aplicamos este cambio a la ecuación de Bellman nos quedaría de la siguiente forma: $$ Q(s,a; \theta ) = r + \gamma * maxQ^{*}(s',a';\theta') $$ Siendo $ Q(s,a; \theta ) $ el valor de Q obtenido de la red neuronal principal para la acción a, y esto seria igual a la recompensa inmediata que obtengo al realizar esa acción más el máximo valor de Q obtenido de la red neuronal objetivo para cualquier acción en el siguiente estado s’. Antes de pasar al procedimiento que sigue el algoritmo vamos a explicar unos conceptos fundamentales a la hora de implementar deep q-learning. ### Replay memory En q-learning el entrenamiento se realizaba actualizando los valores de Q en la tabla cada vez que tomábamos una acción, en el caso de deep q-learning la red neuronal se va entrenando utilizando datos que vamos almacenando en una replay memory, este objeto almacena un numero determinado de transiciones donde en cada transición almacenamos el estado inicial, la acción tomada, la recompensa obtenida y el estado final. Así en cada iteración escogemos transiciones al azar de esta memoria y las utilizamos para entrenar nuestra red principal. ### Exploración Si las acciones que toma nuestro agente son obtenidas únicamente por el máximo valor de Q de nuestra red principal, llegara un momento en el cual nuestro algoritmo repetiría siempre el mismo ciclo de acciones y pasando por los mismos estados sin llegar a maximizar la recompensa. Por esta razón incluimos el concepto de exploración, el cual para cada vez que vayamos a escoger una acción hay una probabilidad de que esta acción sea aleatoria, esta probabilidad es llamada épsilon, de esta forma conseguimos que nuestro modelo explore nuevas opciones y tenga más probabilidades de encontrar su política optima. Este concepto de exploración también se aplica a q-learning. El valor de épsilon al inicio del algoritmo es muy alto para que así aumentar las probabilidades de encontrar el camino ideal y a medida que pasan las iteraciones este valor va decayendo hasta alcanzar un valor mínimo. ### La función de perdida (loss function) Las redes neuronales son entrenadas mediante un descenso de gradientes que va actualizando los pesos de la red neuronal, pero para realizar este descenso necesitamos calcular cual seria la perdida que tiene la red. Esta perdida la calculamos mediante el cuadrado de la diferencia entre el valor de Q que hemos obtenido de la red y el cálculo de la ecuación de Bellman para la recompensa inmediata y futura que obtenemos del estado actual y el siguiente: $$ Loss(\theta ) = E[((r + \gamma * maxQ^{*}(s',a';\theta'))-Q(s,a; \theta ))^{2}] $$ Una vez aclarados los conceptos nuestro algoritmo de deep q-learning quedaría de la siguiente forma: !!!def:Algoritmo Deep Q-learning 1. Iniciamos nuestras redes main y target con los mismos pesos aleatorios. 2. Inicializamos nuestra replay memory con un tamaño máximo N. 3. Iniciamos el entorno partiendo de un estado s. - En base a la probabilidad épsilon elegimos una acción aleatoria o la acción dada por el máximo valor de Q de la red main. - Ejecutamos la acción y obtenemos la recompensa r y el siguiente estado s’ - Almacenamos en nuestra replay memory: (s, a, r, s’) - Si la replay memory contiene las suficientes transiciones elegimos al azar n transiciones. - Calculamos la función de perdida para dichas transiciones. - Realizamos descenso del gradiente con esas pérdidas. - Repetimos desde a hasta alcanzar un estado final. 4. Cada x episodios actualizamos los pesos de la red target con los pesos de main. 5. Repetimos desde 3 el número de episodios que indiquemos al algoritmo. Deep q learning multiagente ============================================================== Hasta ahora hemos visto como realizar aprendizaje por refuerzo para un solo agente en el entorno, pero ¿Qué pasa si tenemos mas agentes que controlar en el entorno? Bien, este problema podemos abordarlo de distintas maneras dependiendo de la naturaleza del problema, por ejemplo, si los agentes tienen que cooperar para conseguir un objetivo en común o compiten entre ellos. 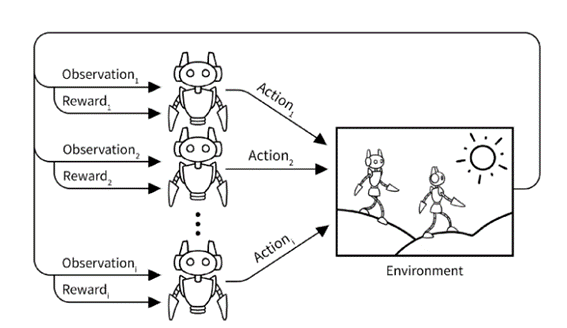Juegos de Markov -------------------------------------------------------------- Los juegos de Markov nos dan una idea de como modelar un sistema multiagente que sea totalmente observable, donde al igual que en los MDP trabajamos con un conjunto de estados, acciones y recompensas. En los juegos de Markov tenemos una tupla de la forma donde I es el conjunto de N agentes, S es un espacio de estado finito, A = A1 × A2 × ... × AN es el conjunto espacio de acción de N agentes, R = (r1, r2, ..., rN ) donde $ Ri : S ×A \rightarrow R $ es el espacio de acción de cada agente función de recompensa, $ T : S × A × S \rightarrow [0, 1] $ es la función de transición y γ es la factor de descuento. En un juego de Markov donde el objetivo sea cooperar los agentes compartirán la función de recompensa y trataran de maximizarla entre ellos, en el caso de que tengan que competir la función de recompensa que reciben se trataría de un juego de suma cero donde las ganancias del otra agente restan las mías. En el caso de los juegos de Márkov todas las acciones se toman simultáneamente.  Como aplicamos deep q-learning -------------------------------------------------------------- Ya tenemos una forma de modelar el problema, pero ¿Cómo se trasladaría esto a deep q-learning? Bien, tenemos varias opciones que podemos tomar dependiendo del problema que queramos modelar. Una opción sería entrenar una única red neuronal y que esta tomara las decisiones para cada uno de los agentes, otra opción seria crear una red para cada uno de los agentes de forma que cada una sea entrenada con la recompensa del propio agente y una última opción seria tener una red neuronal para cada agente pero que estas intercambiaran información durante el entrenamiento.  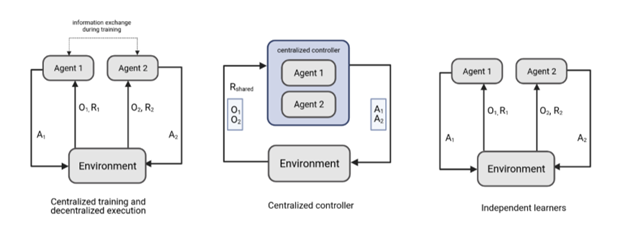En el caso de utilizar la opción de una sola red neuronal el problema se reduciría a un problema de un solo agente, y el algoritmo de deep q-learning seria igual al que vimos en el apartado de deep q-learning, la única diferencia seria que al tomar la decisión de que acción tomar la red se ejecutaría para cada agente a partir de su estado, así yo tendría una sola red que tomara la decisión de cada agente compartiendo entre ellos la misma recompensa. Esta forma de modelar resulta muy ineficiente para un problema multiagente competitivo. En el caso de utilizar varias redes neuronales cada uno de ellos tendría su propia red neuronal, su propia replay memory y su propia función de recompensa. En este caso cada red recibe el estado de su agente y toma la decisión para el mismo, recibiendo una recompensa única para cada agente, de esta forma cada agente es entrenado de forma independiente al resto con lo que conseguimos mejorar la resolución del problema en comparación con el caso anterior, el lado negativo de esto es que se requeriría una mayor carga computacional. El algoritmo en este caso pasaría a ser de la siguiente forma: !!!def:Algoritmo Deep Q-learning Multiagente 1. Iniciamos nuestras redes main y target para cada uno de nuestros agentes, las denotaremos como mi y ti. 2. Inicializamos nuestra replay memory con un tamaño máximo N para cada agente, las denotaremos como rmi. 3. Iniciamos el entorno. - Para cada agente realizamos lo siguiente: - En base a la probabilidad épsilon elegimos una acción aleatoria o la acción dada por el máximo valor de Q de la red mi. - Ejecutamos en paralelo todas las acciones de cada agente y obtenemos la lista de recompensas. - Para cada agente - Obtenemos la recompensa ri y el siguiente estado s’i - Almacenamos en rmi: (si, ai, ri, s’i) - Si rmi contiene las suficientes transiciones elegimos al azar n transiciones. - Calculamos la función de perdida para dichas transiciones. - Realizamos descenso del gradiente en mi con esas pérdidas. - Repetimos desde a hasta alcanzar un estado final. 4. Cada x episodios actualizamos los pesos de ti con los pesos de mi. 5. Repetimos desde 3 el número de episodios que indiquemos al algoritmo. Referencias ============================================================== - [Procesos de decision de Markov](https://medium.com/aprendizaje-por-refuerzo-introducci%C3%B3n-al-mundo-del/aprendizaje-por-refuerzo-procesos-de-decisi%C3%B3n-de-markov-parte-1-8a0aed1e6c59) - [Procesos de decision de Markov SVRAI](https://www.cs.us.es/~fsancho/Cursos/SVRAI/MDP.md.html) - [Redes neuronales wikipedia](https://es.wikipedia.org/wiki/Red_neuronal_artificiale) - [Redes neuronales convolucionales](https://bootcampai.medium.com/redes-neuronales-convolucionales-5e0ce960caf8 ) - [Multiagent Deep Reinforcement Learning: Challenges and Directions Towards Human-Like Approaches](https://arxiv.org/pdf/2106.15691.pdf) - [Multi-Agent Deep Reinforcement Learning in 13 Lines of Code Using PettingZoo](https://towardsdatascience.com/multi-agent-deep-reinforcement-learning-in-15-lines-of-code-using-pettingzoo-e0b963c0820b) - [REINFORCEMENT LEARNING (DQN) TUTORIAL PYTORCH](https://pytorch.org/tutorials/intermediate/reinforcement_q_learning.html) ---