X | Agentes Lógicos: Lógica Epistémica y Temporal en Sistemas Multiagente
Como hemos ido tratando en capítulos previos, el marco de los Sistemas Multi-Agente (MAS) se ha utilizado para formalizar diversos problemas en la informática, la inteligencia artificial, la teoría de los juegos, la teoría de la elección social y otras disciplinas relacionadas. Hasta ahora, hemos presentado los sistemas multiagente casi como un paradigma para la computación, la programación y/o el diseño. Sin embargo, este campo proporcionan además un paradigma para hablar del mundo, mediante un lenguaje y una estructura conceptual específica subyacente al mismo. Además, es habitual que los componentes de estos sistemas sean autónomos, quizás inteligentes, definitivamente activos e incluso proactivos, con algunos objetivos y creencias sobre el mundo (habitualmente incompletas y/o bajo incertidumbre). Los métodos basados en la lógica para los sistemas multiagente tienen varias ventajas. La lógica proporciona un vocabulario para nombrar las propiedades de los sistemas, y el vocabulario recibe un significado preciso a través de modelos y reglas semánticas. Además, los modelos lógicos proporcionan un aparato conceptual para el razonamiento que puede utilizarse también fuera de la lógica matemática. En este capítulo (y el siguiente) nos centramos en la Lógica Modal, que proporciona una maquinaria conceptual que permite describir de distintos *modos* la semántica del mundo posible (también conocida como semántica de Kripke). El desarrollo de este área de la Lógica ha dado lugar a distintos sistemas formales centrados en diferentes aspectos del comportamiento humano y el comportamiento del mundo en general: Lógica epistémica (o Lógica del conocimiento), Lógica doxástica (o lógica de las creencias), Lógica deóntica (o Lógica de las obligaciones), Lógica dinámica (o Lógica de las acciones), Lógica temporal (o Lógica del tiempo), Lógica estratégica y combinaciones de las anteriores (por ejemplo, la Lógica BDI). En el contexto de los MAS, mostraremos que muchos de los problemas relacionados con los mecanismos de razonamiento y resolución de juegos tienen una interpretación natural en problemas de decisión para la lógica de los agentes. Normalmente, el punto de partida es describir una propiedad deseable en el lenguaje lógico. A continuación, podemos comprobar si la propiedad se cumple en el modelo de un sistema dado, en todos los modelos posibles de todos los sistemas posibles, o en al menos un sistema posible (que se espera que sea sintetizado y devuelto por el proceso de comprobación). O, a la inversa, se puede especificar una propiedad peligrosa y comprobar si el peligro se aplica al sistema en cuestión, a todos los sistemas posibles o al menos a un escenario vulnerable. X.1 Aspectos formales de la Lógica Modal ---------------------------------------------------------------Sintáxis
Formalmente, la Lógica Modal es una extensión de las Lógicas Clásicas (Proposicional, de Primer Orden, de Orden Superior). Sintácticamente, siguen las reglas y operadores de las Lógicas Clásicas e incorporan nuevos operadores. Originalmente, la Lógica Modal incorporaba dos operadores \(\Box\) y \(\Diamond\), que reflejaban la necesidad y posibilidad de que una fórmula \(\varphi\) fuese cierta. En realidad, sería suficiente contar con uno sólo de los anteriores operadores, ya que, a falta de definir formalmente la semántica, resulta intuitivo pensar que ambos operadores son duales, esto es : \[\Diamond \varphi \leftrightarrow \neg \Box \neg \varphi \]Semántica
Formalmente, la semántica de la Lógica Modal (básica) suele definirse a través de la Semántica Kripke, desarrollada a mediados del siglo XX por Saul Kripke y André Joyal. !!!def: *Def. X.1* - Semántica Kripke (también Semántica relacional o Semántica marco) Dado el conjunto de fórmulas atómicas \(\mathcal{PV} = \{p_1, p_2, \dots \}\): - Un *marco Kripke* es un par \(F = \left\langle \mathcal{W}, \mathcal{R}\right\rangle\) donde $\mathcal{W}=\{w_1, w_2, \dots, w_k\}$ corresponde al conjunto mundos posibles y $\mathcal{R} \subseteq \mathcal{W} \times \mathcal{W}$ es una relación binaria (habitualmente llamada relación de accesibilidad). Es habitual dar representaciones para los marcos en forma de grafos dirigidos con propiedades en el que los nodos corresponden a los mundos y las aristas a las relaciones de accesibilidad entre los mundos. - Un *modelo Kripke* es un par \(M = \left\langle F, \mathcal{V}\right\rangle\) tal que \(F = \left\langle \mathcal{W}, \mathcal{R}\right\rangle \) corresponde a un marco Kripke y \(\mathcal{V}: \mathcal{PV} \rightarrow \mathcal{P}(\mathcal{W})\) una función de valoración de las fórmulas atómicas que indica, para cada una de ellas, en qué mundos son ciertas. Del mismo modo que en otras Lógicas se define la evaluación de las fórmulas a través de los valores de verdad de las fórmulas atómicas y ciertas funciones de verdad asociadas a los operadores (conectivas, cuantificadores, etc.), en la Lógica Modal también se evalúan las fórmulas respecto de modelos y de marcos. De hecho, las estructuras de las interpretaciones de la lógica de predicados y las estructuras de los marcos y modelos de la lógica modal guardan, en realidad, una muy estrecha relación entre sí. !!!def: *Def. X.2* - Verdad Local (Satisfactibilidad \(\models\)) Dado un modelo Kripke \(M = \left\langle \mathcal{W}, \mathcal{R}, \mathcal{V}\right\rangle\) y un mundo $w \in \mathcal{W}$, el valor de verdad asociado a una fórmula de la Lógica Modal (en su versión proposicional) corresponde a: \[ \begin{array}{l c l} M,w \models p \in \mathcal{PV} & \iff & w \in \mathcal{V}(p)\\ M,w \models \neg \varphi & \iff & M,w \not \models \varphi\\ M,w \models \varphi \wedge \psi & \iff & M,w \models \varphi \wedge M,w \models \psi \\ M,w \models \varphi \vee \psi & \iff & M,w \models \varphi \vee M,w \models \psi \\ M,w \models \Box \varphi & \iff & \textit{para cada } w' \in \mathcal{W} \textit{ tal que } w \mathcal{R} w' \textit{ se tiene } M,w' \models \varphi\\ M,w \models \Diamond \varphi & \iff & \textit{para algún } w' \in \mathcal{W} \textit{ tal que } w \mathcal{R} w' \textit{ se tiene } M,w' \models \varphi\\ \end{array} \] Nótese que de la segunda condición es fácil notar que para ningún \(w \in \mathcal{W}\) se tiene \(M,w \models \perp\), dado que \(\mathcal{W}\) es el conjunto de los mundos posibles (consistentes). Además nótese que la noción de verdad presentada es de carácter *local* a un mundo \(w\) de un modelo \(M\). Esta definición puede asimilarse al concepto de satisfactibilidad que conocemos en las Lógicas Clásicas. !!!def: *Def. X.3* - Verdad Global (Validez débil) Dado un modelo Kripke \(M = \left\langle \mathcal{W}, \mathcal{R}, \mathcal{V}\right\rangle\), una fórmula \(\varphi\) se dice verdadera en \(M\), y se nota por \(M \models \varphi \), si es localmente verdadera para todo mundo posible \(w \in \mathcal{W}\) del modelo \(M\). Ahora bien, puede ser preciso conocer información no sólo sesgada a un modelo considerado, sino averiguar qué fórmulas son verdaderas con respecto a la estructura del marco. Esta es una noción de verdad, es *más fuerte*, más cercana al concepto de validez lógica en la Lógica Clásica, pues se enfoca en la estructura (más *sólida*, *estática*, o *fija*) y no en las valuaciones (más *dinámicas*, o *volátiles* que pueden ser adecuadas o no). !!!def: *Def. X.4* - Validez Dado un marco Kripke \(F = \left\langle \mathcal{W}, \mathcal{R}\right\rangle\), una fórmula \(\varphi\) se dice: 1. válida en un mundo \(w\), notado por \(F,w \models \varphi\), si para todo modelo \(M=\left\langle F, \mathcal{V}\right\rangle\) se tiene \(M,w \models \varphi\), esto es, si \(\varphi\) es localmente verdadera en \(w\) para todo modelo \(M\) basado en \(F\); 2. válida en un marco \(F\), notado por \(F \models \varphi\), si para todo \(w \in \mathcal{W}\) se tiene \(F,w \models \varphi\), o sea, si es válida en todo mundo del marco; 3. válida en una clase de estructuras (marcos/modelos) \(\mathcal{S}\), notado por \(\mathcal{S} \models \varphi\) si es válida para cualquier marco/modelo de la clase; 4. válida, notado por \(\models \varphi\), si es válida para cualquier marco. Al igual que en la Lógica Clásica, también existe la noción de consecuencia Lógica, trasladada a la Lógica Modal en dos ámbitos, uno local y otro global. !!!def: *Def. X.5* - Consecuencia lógica - (Local) Dado un conjunto de fórmulas \(\Sigma\) y una fórmula \(\varphi\) en una clase de estructuras (marcos/modelos) \(\mathcal{S}\), se dice que \(\varphi\) es consecuencia lógica local de \(\Sigma\) en \(\mathcal{S}\), y se nota por \(\Sigma \models_{\mathcal{S}} \varphi\) si para todo modelo \(M\) asociado a \(\mathcal{S}\) y todo mundo \(w\) de \(M\) si \(M,w \models \Sigma\) entonces \(M,w \models \varphi\). - (Global) Dado un conjunto de fórmulas \(\Sigma\) y una fórmula \(\varphi\) en una clase de estructuras (marcos/modelos) \(\mathcal{S}\), se dice que \(\varphi\) es consecuencia lógica global de \(\Sigma\) en \(\mathcal{S}\), y se nota por \(\Sigma \models_{\mathcal{S}}^{g} \varphi\) si para toda estructura \(S\) de \(\mathcal{S}\) si \(S \models \Sigma\) entonces \(S \models \varphi\).Lógica Modal Normal, El sistema K y la Teoría de la Correspondencia
Al igual que en los demás sistemas formales, hemos de plantearnos si existe un procedimiento de cálculo que permita derivar o deducir nuevas verdades en los modelos Kripke. Aunque de forma general, según las definiciones dadas, para poder razonar en una Lógica Modal hemos de chequear las propiedades y las relaciones según el marco o el modelo. Ya se ha visto con anterioridad que pueden existir fórmulas válidas en las estructuras. Consideremos, que una cierta fórmula \(\varphi\) es válida en el conjunto de modelos asociados a una clase (de marcos o modelos), entonces podríamos decir que \(\varphi\) captura de cierta manera una propiedad subyacente a la estructura. Además, si ese conjunto de modelos es maximal (no existe otro no incluido en el conjunto tal que la fórmula sea válida en él) podemos decir no sólo que el conjunto posee la propiedad reflejada por \(\varphi\), sino también que esta fórmula modal caracteriza (sintácticamente) a todo ese conjunto, dando lugar a distintas Lógicas modales. !!!def: *Def. X.6* - Lógica Modal Una Lógica modal \(\mho\) es un conjunto de fórmulas bien formadas que contiene a todas las tautologías (según el tipo de lógica base) es cerrado bajo *modus ponens* y bajo sustitución uniforme. A cada fórmula, \(\varphi\), válida en \(\mho\) se le denomina teorema de \(\mho\) (y se denota por \(\vdash_{\mho} \varphi\)). Veremos ahora algunos de los axiomas más corrientes y que dan lugar a toda una clase de Lógicas Modales denominadas normales, con distinto grado de restricción en las estructuras de la Lógica. !!!def: *Def. X.7* - Lógica Modal Normal Una Lógica modal \(\mho\) se dice normal si cumple dos condiciones: 1. \(\vdash_{\mho} \Box(\varphi \rightarrow \psi) \rightarrow (\Box \varphi \rightarrow \Box \psi) \) (**Axioma \(K\)**) 2. \( \vdash_{\mho} \varphi \implies \vdash_{\mho} \Box \varphi \) (**Regla de necesidad**) El sistema más general dentro de las Lógicas modales normales es el *Sistema \(K\)*, en el que el único axioma de dicha Lógica es, precisamente, el axioma \(K\). A partir de éste, mediante extensión de los axiomas, se han desarrollado un conjunto de Lógicas modales normales \(K\Sigma_1\Sigma_2...\) basados en distintas propiedades de la relación de accesibilidad (reflexividad,transitividad, serialidad, ...). La *Teoría de la Correspondencia* estudia precisamente esa caracterización de las propiedades y las fórmulas modales. Algunos de los axiomas y extensiones \(K\Sigma_1\Sigma_2...\) más utilizadas: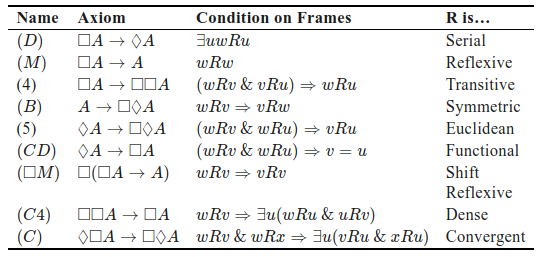
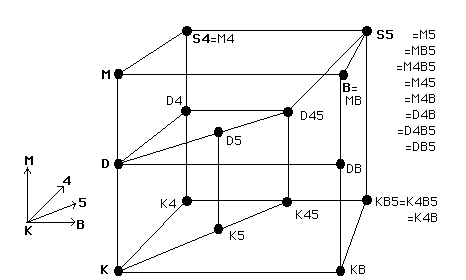
Corrección, Completitud y Complejidad de los Sistemas normales
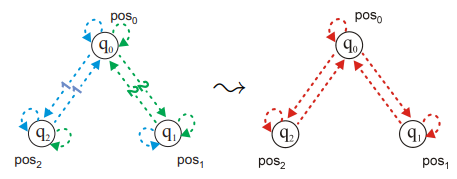
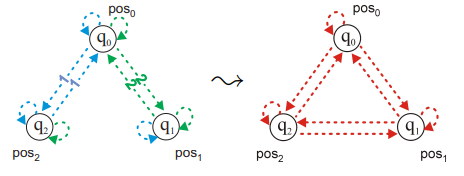
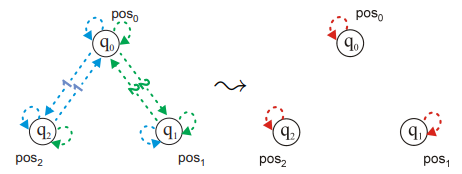
La relación entre el aspecto sintáctico y el aspecto semántico de las Lógicas modales nos lleva a considerar resultados de corrección (o adecuación, o soundness) y completitud (completeness) de dichas Lógicas. Intuitivamente sabemos que la relación entre sintaxis y semántica debe ser tal que los teoremas que derivamos en la lógica son verdaderos (corrección) y que todas las fórmulas verdaderas son derivables sintácticamente (completitud). !!!ERROR: Teorema de Corrección y Completitud en \(K\) El sistema K es correcto y completo con respecto a modelos de Kripke arbitrarios. Si permitimos \(n\) modalidades, tanto el teorema como las definiciones se extienden de manera natural. La técnica de prueba que se usa para demostrar el Teorema de completitud de \(K\) se conoce como Prueba de Completitud por canonicidad. (Puedes consultar algunos detalles de esta prueba en [#3], basados en los *Modelos canónicos*, el *Lema de Lindenbaum* y el *Lema de Verdad*). Como extensión del teorema previo se tiene también: !!!ERROR: Teorema de Corrección y Completitud en Lógicas \(K\Sigma_1\Sigma_2...\) Sea \(\boldsymbol{X}\) cualquier subconjunto de \(\{D,T,4,5\}\) y \(\mathcal{X}\) el conjunto de propiedades de relación correspondientes a \(\boldsymbol{X}\). Se tiene que \(\boldsymbol{K} \cup \boldsymbol{X}\) es correcto y completo respecto del conjunto de modelos Kripke cuya relación de accesibilidad satisface \(\mathcal{X}\) Otro aspecto que ha de ser evaluado es el carárcter decidible de las Lógicas Modales, así como la complejidad asociada a los procedimientos de las mismas. Sabemos que un conjunto de fórmulas es decidible si existe un procedimiento (un método finito y efectivo de decisión) para determinar si cualquier fórmula del lenguaje pertenece a dicho conjunto. De ahí, una Lógica Modal es decidible si el problema de la satisfactibilidad es decidible. Precisamente, un instrumento para demostrar la decidibilidad de una Lógica es la Propiedad de Modelo Finito. !!!def: *Definición X.7*- Propiedad de Modelo Finito Sea \(\mho\) una lógica, y $\mathcal{M} una clase de modelos para \(\mho\) . Decimos que \(\mho\) tiene la propiedad de modelo finito con respecto a \(M\) si dada una fórmula \(\varphi\) de \(\mho\) que es satisfactible en algún modelo en \(M\) entonces es también satisfactible en un modelo finito en \(M\). Un modelo es finito si su conjunto de mundos \(\mathcal{W}\) tiene una cantidad finita de elementos, si no el modelo es infinito. Además no es difícil probar (utilizando la técnica de filtrado) que la Lógica \(K\) (y por ende sus extensiones) son decidibles. Puedes consultar la prueba detallada en [#3]. X.2 Lógica Epistémica como Lógica Modal Normal --------------------------------------------------------------- La lógica epistémica se ocupa de la especificación y el razonamiento sobre el conocimiento de los agentes. Las propiedades epistémicas tienen una interpretación sencilla en la lógica modal, y al mismo tiempo son muy importantes para el razonamiento sobre la interacción entre agentes. Utilizaremos la lógica epistémica para presentar ejemplos de propiedades y mostrar cómo se evalúan en modelos de sistemas multiagente sencillos. La Lógica epistémica básica que consideramos aquí implica operadores de necesidad modal para el conocimiento individual. Por razones históricas y de mayor legibilidad, se utiliza \(K\) en lugar de \(\Box\) para las modalidades de conocimiento, de forma que \(K \varphi\) se interpreta como *el agente conoce \(\varphi\)*. Además hemos de considerar, para el caso multiagente (con \(n\) agentes), una versión extendida de la Lógica modal, tanto en los operadores como en las estructuras. - En el caso de los operadores se considera un operador \(K_i\) para cada agente, que denota *el agente i conoce ...* - En el modelo no cambia (como par (marco, valoración)), pero el marco sí es extendido como\(\left\langle \mathcal{W}, \mathcal{R}_1, \mathcal{R}_2, \dots, \mathcal{R}_n\right\rangle\) en el que cada \(\mathcal{R}_i\) corresponde a la relación de accesibilidad del agente \(i\)(posiblemente distinta para cada agente). - La semántica es extendida naturalmente al caso multi-modal, remplazando adecuadamente las definiciones según las extensión de la relación de accesibilidad. \[M, w \models K_i \varphi \iff \textit{ para cada } w' \textit{ tal que } w \mathcal{R}_i w' \textit{ se tiene } M,w' \models \varphi\] Además, se pueden considerar modalidades de conocimiento colectivo de grupos de agentes: conocimiento mutuo (\(E_A \varphi\): *todos en el grupo \(A\) saben que \(\varphi\)*, \(\mathcal{R}_{E_A} = \bigcup_{i \in A} \mathcal{R}_i\)), conocimiento común conocimiento común (\(C_A \varphi\): *todos los agentes de \(A\) saben que \(E_A \varphi\)*, \(\mathcal{R_{C_A}} = CT(E_A)\)), y el conocimiento distribuido (\(D_A\varphi\): *si los agentes compartieran su información disponible, serían capaces de reconocer que \(\varphi\)*, \(\mathcal{R}_{D_A} = \bigcap_{i \in A} \mathcal{R}_i\)). La semántica asociada a dichos operadores viene dada por: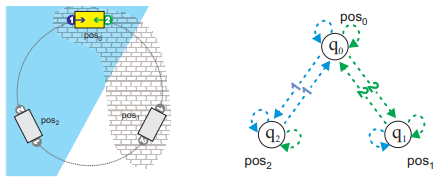
Model Checking Local/Global
Hay varias formas de verificar la corrección de un sistema. La más popular y exitosa es técnica de *Model Checking*, que responde a si una fórmula dada \(\varphi\) se cumple en un estado \(w\) del modelo \(M\). Formalmente, la comprobación del modelo es el problema de decisión que determina la pertenencia al conjunto:\[MC(\mathcal{L}, \mathcal{S}, \models ) = \left\lbrace ((M,w), \varphi) \in \mathcal{S} \times \mathcal{L} \, \vert \, M,w \models \varphi \right\rbrace\] Donde \(\mathcal{L}\) corresponde a un lenguaje lógico, \(\mathcal{S}\) a una estructura de modelos para \(\mathcal{L}\) y \(\models\) una relación de satisfacción semántica compatible con \(\mathcal{L}\) y \(\mathcal{S}\). Así, un procedimiento de resolución de dicho problema de decisión responderá *Sí* si y sólo si \(M,w \models \varphi\). Esta variante del problema se denomina a veces comprobación del modelo local para destacar que el valor de \(\varphi\) se calcula para un estado particular del sistema. A menudo es útil calcular el conjunto de estados en \(M\) que satisfacen la fórmula \(\varphi\) en lugar de de comprobar si \(\varphi\) se cumple en un estado determinado. Esta variante del problema se conoce como comprobación del modelo global. Para los problemas de verificación que consideraremos aquí, las complejidades de la comprobación de modelos local y global coinciden, y los algoritmos para una variante de la comprobación de modelos pueden adaptarse de forma sencilla a la otra variante. En consecuencia, utilizaremos ambas nociones de comprobación de modelos indistintamente.Modal Checking en la Lógica Epistémica
La comprobación de modelos de la lógica epistémica es bastante sencilla. Aun así, es instructivo comenzar nuestro estudio de los algoritmos de verificación con el caso simple. A continuación, presentamos el algoritmo recursivo para la comprobación del modelo local de las propiedades relacionadas con el conocimiento.Es fácil notar que los casos del algoritmo simplemente mapean las respectivas definiciones semánticas de lógica epistémica a una forma ejecutable. !!!code: Función \(mcheck(M,w,\varphi)\) - \(\varphi \equiv p \Rightarrow mcheck(M,w,\varphi) = w \in \mathcal{V}(p)\) - \(\varphi \equiv \neg \psi \Rightarrow mcheck(M,w,\varphi) = \neg \, mcheck(M,w,\psi)\) - \(\varphi \equiv \psi \wedge \chi \Rightarrow mcheck(M,w,\varphi) = mcheck(M,w,\psi) \wedge mcheck(M,w,\chi) \) - \(\varphi \equiv \psi \vee \chi \Rightarrow mcheck(M,w,\varphi) = mcheck(M,w,\psi) \vee mcheck(M,w,\chi) \) - \(\varphi \equiv K_i \psi \Rightarrow mcheck(M,w,\varphi) = \bigwedge_{\{w' \in \mathcal{W} \, | \, w \mathcal{R_i} w' \}} mcheck(M,w',\psi) \) - \(\varphi \equiv \overline{K}_i \psi \Rightarrow mcheck(M,w,\varphi) = \bigvee_{ \{w' \in \mathcal{W} \, | \, w \mathcal{R_i} w' \}} mcheck(M,w',\psi) \) En vez de \(K_i\), a veces es más conveniente el uso del operador dual *posiblemente conoce*, notado por \(\overline{K}_i\) y definido formalmente como \( \overline{K}_i \varphi \equiv \neg K_i \neg \varphi \). De forma análoga, un algoritmo para el model checking global, que toma un modelo y una fórmula como entrada y devuelve el subconjunto exacto de estados del modelo que satisfacen la fórmula, se puede obtener de las operaciones lógicas de la comprobación del modelo local a sus equivalentes en la teoría de conjuntos.Por lo tanto, el algoritmo para la comprobación del modelo epistémico queda como: !!!code: Función \(mcheck(M,\varphi)\) - \(\varphi \equiv p \Rightarrow mcheck(M,\varphi) = \mathcal{V}(p)\) - \(\varphi \equiv \neg \psi \Rightarrow mcheck(M,\varphi) = \mathcal{W} \setminus check(M,\psi)\) - \(\varphi \equiv \psi \wedge \chi \Rightarrow mcheck(M,\varphi) = mcheck(M,\psi) \cap mcheck(M,\chi) \) - \(\varphi \equiv \psi \vee \chi \Rightarrow mcheck(M,\varphi) = mcheck(M,\psi) \cup mcheck(M,\chi) \) - \(\varphi \equiv K_i \psi \Rightarrow mcheck(M,\varphi) = \{w \in \mathcal{W} \, | \, \forall w' \in \mathcal{W} : w\mathcal{R}_{i}w' \rightarrow mcheck(M,\psi) \} \) - \(\varphi \equiv \overline{K}_i \psi \Rightarrow mcheck(M,\varphi) = \{w \in \mathcal{W} \, | \, \exists w' \in \mathcal{W} : w\mathcal{R}_{i}w' \wedge mcheck(M,\psi) \} \) !!!Tip: (Ejemplo) Robots y carro: Model checking Considerando el ejemplo anterior de los Robots y el carro, mostremos cuál sería la ejecución del algoritmo de global model checking para la fórmula \(K_1 \neg pos_2\).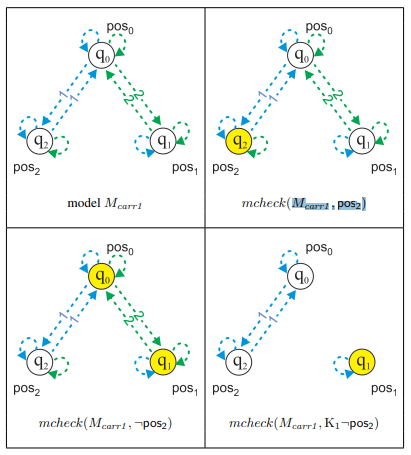
Lógica Dinámica Proposicional (PDL)
La lógica dinámica proposicional (PDL), que fue diseñada principalmente para razonar sobre programas de ordenador, es probablemente el representante más típico de las Lógicas con acciones. Las acciones se representan en el lenguaje mediante etiquetas de acción \(\alpha_1\), \(\alpha_2\), ..., \(alpha_n\) de un conjunto finito *Act*. También se pueden construir términos de acción complejos, por ejemplo, la composición secuencial \((\alpha_1; \alpha_2)\), elección no determinista \((\alpha_1 \cup \alpha_2)\), iteración finita \((\alpha∗)\), etc. Ahora bien, \([\alpha]\varphi\) expresa el hecho de que \(\varphi\) está obligado a mantenerse después de cada ejecución de \(\alpha\), y \(\langle \alpha \rangle \varphi \equiv \neg [\alpha] \neg \varphi\) dice que \(\varphi\) se mantiene después de al menos una posible ejecución de \(\alpha\). En el contexto semántico, los modelos vienen dados a partir de los llamados Sistemas de transición etiquetados, !!!def: *Definición X.8* - Sistema de transición etiquetado Un *Sistema de transición etiquetado* corresponde a una \(n+1\)-tupla \(\left\langle St, \xrightarrow[]{\alpha_1}, \dots, \xrightarrow[]{\alpha_n}, \right\rangle\) tal que \(St\) es un conjunto no vcío de estados y las relaciones de accesibilidad modelan las transformaciones entre estados de forma no determinista. \(\xrightarrow[]{\alpha_i} \subseteq St \times St \). Con esto, los modelos asociados amplian los sistemas de transición con la valoración de proposiciones atómicas, \(\mathcal{V}\), y la semántica corresponde, de manera análoga a lo ya presentado en otras lógicas, a:Lógica Temporal
La lógica temporal deja implícitas las acciones, y en su lugar se centra en los posibles patrones de evolución. Los operadores temporales típicos son: |Operador|Descripción| |:------:|:---------:| | \(X \varphi \) | \(\varphi\) será cierto en el siguiente instante de tiempo | | \(G \varphi \) | \(\varphi\) será cierto en todos los instantes a partir de ahora | | \(F \varphi \) | \(\varphi\) es cierto o será cierto en algún instante futuro | | \(\varphi\, U \,\psi \) | \(\psi\) será cierto en algún instante futuro y hasta ese instante \(\varphi\) será cierto |Propiedades del tiempo
La Lógica temporal se desarrolló originalmente para representar la tensión en el lenguaje natural. Dentro de las ciencias de la computación, ha logrado un éxito significativo en la especificación formal y verificación de sistemas concurrentes y distribuidos. Gran parte de su popularidad se debe a que algunos conceptos útiles pueden especificarse formal y de forma concisa mediante la Lógica Temporal, más concretamente, propiedades de seguridad, vivacidad, y equidad. - Las propiedades de seguridad corresponden a los objetivos de mantenimiento y se refieren a un estado de cosas que debe preservarse (o evitarse) durante toda la vida útil del sistema. Es decir, corresponden a afirmaciones como: *algo malo nunca ocurrirá* o *algo bueno siempre se mantendrá*. Como ejemplo, \(G \neg bancarrota\) puede utilizarse para exigir que yo nunca quebraré. Del mismo modo, \(G(fuelOK \vee X fuelOK)\) expresa que el depósito de combustible nunca estará vacío durante más de una unidad de tiempo. Por lo tanto, el modelo temporal para la seguridad es \(G\varphi\). - Las propiedades de vivacidad corresponden a objetivos de logro, y se refieren a un estado de cosas que debe alcanzarse en algún momento en el futuro (*algo bueno sucederá*). Por ejemplo, \(F rich\) puede utilizarse para expresar que en algún momento seré rico. Mejor aún, \(F G rich\) requiere que me haré y me mantendré rico a partir de algún momento. Por último, \(solicitado \rightarrow F concedido\) dice que si se solicita un recurso ahora, se concederá tarde o temprano. Así, el modelo temporal de las propiedades de vivacidad es \(F\varphi\). - Las propiedades de equidad corresponden a objetivos de servicio, y se refieren a cualidades que deben ser proporcionadas con suficiente frecuencia. Normalmente, se corresponden con afirmaciones como *Siempre que se intente/solicite algo, se conseguirá/será concedido*. Por ejemplo, \(G F rich\) puede utilizarse para expresar que, aunque sea pobre en el futuro, siempre siempre me recuperaré y volveré a ser rico. Alternativamente, puede leerse como *Seré rico infinitamente a menudo*. \(G(intento \rightarrow F éxito)\) dice que siempre que se intente una acción, finalmente tendrá éxito. Una propiedad más débil, \( (G F intento) \rightarrow (G F éxito)\), expresa que si la acción se intenta infinitamente a menudo, también tendrá éxito infinitamente con infinita frecuencia. Así, los modelos temporales de las propiedades de equidad son \(G F \varphi\) y \(G(\varphi \rightarrow F \psi)\) . Las propiedades de equidad son útiles cuando se especifican propiedades para programar procesos, responder a mensajes, etc. Lo más importante es que pueden utilizarse para especificar propiedades del entorno en el que operan los agentes.Modelos de tiempo
Los modelos de Lógica temporal incluyen una relación de transición, y vienen en dos versiones. Los modelos temporales lineales definen una ordenación total de los mundos posibles (*momentos temporales*), de modo que un modelo puede verse como un único camino infinito \(\lambda\) con estados sucesivos \(\lambda[0]\), \(\lambda[1]\), ... . Los modelos de tiempo ramificado, en cambio, consisten en un árbol que encapsula todas las posibles evoluciones del sistema. En cierto modo, se supone que un modelo de tiempo lineal captura lo que que ocurrirá en el sistema a partir de ahora, mientras que un árbol de tiempo ramificado captura lo que puede ocurrir. Estos modelos infinitos del futuro suelen denominarse estructuras de comportamiento de la evolución temporal. Obviamente, al razonar sobre las propiedades de un sistema concreto, un modelo dado en forma de camino infinito o de árbol infinito sería poco práctico. En su lugar, el comportamiento del sistema suele representarse por un Modelo Kripke de transición sobre un Sistema de transición no etiquetado. !!!def: *Definición X.9* - Sistema de transición no etiquetado Un *Sistema de Transición No Etiquetado* corresponde a un par \(\left\langle St, \longrightarrow \right\rangle\) tal que \(St\) es un conjunto no vacío de estados y la relación de accesibilidad modela las transformaciones entre estados de forma no necesariamente determinista. \(\longrightarrow \subseteq St \times St\). !!!Tip: (Ejemplo) Robots y carro II Consideremos la siguiente variación del escenario de los robots y el carro. Ahora, el robot 1 puede empujar el carro para que se mueva en el sentido de las agujas del reloj. También puede abstenerse de empujar, en cuyo caso el carro no se mueve. El robot 2, por tanto, no influye en la posición del carro. Mostramos cómo la estructura computacional da lugar a modelos de comportamiento de y de ramificación en la figura. En la parte izquierda, se presenta el modelo de tiempo lineal para que el carro permanezca en la posición 0 durante dos momentos, y luego se mueva a la posición 1. En la parte derecha se presenta el modelo de tiempo de ramificación que supone que \(q_0\) es el estado inicial del sistema.
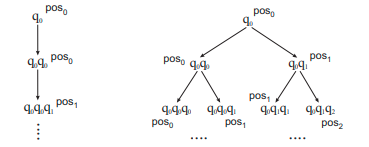
Lógica Temporal Lineal (LTL)
Extensión de la Lógica Proposicional añadiendo los operadores temporales \(X\) y \(U\), a partir de los cuales pueden definirse (eventualmente cierto) \(F \varphi \equiv \top\, U \,\varphi \), (en adelante siempre cierto) \(G \varphi \equiv \neg F \neg \varphi \), (\(U\) débil) \( \varphi W \psi \equiv (\varphi\, U \,\psi) \vee G\varphi\), (*release*) \(\varphi R \psi \equiv \psi W (\varphi \wedge psi)\). La semántica de LTL se define típicamente en modelos de comportamiento, es decir, caminos infinitos de un modelo de transición de Kripke \(M\). Sea \(\lambda\) un camino en \(M\). Se define: - \(\lambda[i]\) como el \(i\)-ésimo estado de \(\lambda\) (siendo el estado inicial \(\lambda[0]\)). - \(\lambda[i..j]\): el fragmento del camino desde el \(i\)-ésimo al \(j\)-ésimo estado del camino. - \(\lambda[i...]\): el fragmento del camino desde el \(i\)-ésimo estado del camino en adelante. De manera que la semántica asociada quedaría como: - \(\lambda \models p \iff \lambda[0] \in \mathcal{V}(p)\), con \(p\) una fórmula atómica y \(V\) una función que asigna a cada estado un conjunto de fórmulas atómicas (etiquetas) verdaderas en él. - \(\lambda \models \neg \varphi \iff \lambda \not \models \varphi \) - \(\lambda \models \varphi \wedge \psi \iff \lambda \models \varphi \wedge \lambda \models \psi \) - Similar para el resto de conectivas proposicionales - \(\lambda \models X \varphi \iff \lambda[1...] \models \varphi \) - \(\lambda \models \varphi\, U \,\psi \iff \exists i \geq 0 \, | \, \lambda[i...] \models \psi \wedge \forall j < i : \lambda[j..] \models \varphi \) - \(\lambda \models F \varphi \iff \exists i \geq 0 \, | \lambda[i...] \models \varphi \) - \(\lambda \models G \varphi \iff \forall i \geq 0 : \lambda[i...] \models \varphi \) - \(\lambda \models \varphi W \psi \iff \forall i = 0, \dots , j -1 : \lambda[i...] \models \varphi\) con \(j\) el primer momento tal que \(\lambda[j...] \models \psi\) e.o.c. \(j = \infty\) - \(\lambda \models \varphi R \psi \iff \forall i = 0, \dots , j : \lambda[i...] \models \psi\) con \(j\) el primer momento tal que \(\lambda[j...] \models \varphi\) e.o.c. \(j = \infty\) !!!Tip: (Ejemplo) Robots y carro II Consideremos el camino \(\lambda = (q_0q_1q_2)^{\infty} = q_0 q_1 q_2 q_0 q_1 q_2 q_0 q_1 q_2 \dots\) en el modelo de transición de Robots y Carro. Para ese camino, tenemos por ejemplo que \(\lambda \models F pos_2\) (la posición 2 se alcanzará eventualmente), e incluso \( \lambda \models G F pos_2\) (la posición 2 se alcanzará infinitas veces). Sin embargo, no se da el caso de que el carro se detenga y se quede definitivamente en la posición 0, esto es \( \lambda \not \models F G pos_0\). !!!def: *Definición X.10* - Semántica de LTL en modelos de Kripke Sea \(M\) un modelo de transición de Kripke, \(q\) un estado en \(M\), y \(\varphi\) una fórmula de LTL. Decimos que \(\varphi\) se cumple en \(M\), \(q\) (escrito \(M, q \models \varphi \iff \lambda \models \varphi\) para todo camino \(\lambda\) en \(M\) que parta de \(q\). !!!Tip: (Ejemplo) Robots y carros II Para el modelo de transición de Kripke \(M\) presentado en este tema, tenemos por ejemplo que \(M , q_0 \not\models F pos_2\). Nótese que esto no implica que \(M, q_0 \models \neg F pos_2\); por el contrario, también se da el caso de que \(M , q_0 \not\models \neg F pos_2\). Del mismo modo, \(M , q_0 \not\models G pos_0\) y \(M , q0 \not\models \neg G pos_0\). Un ejemplo de fórmula que sí se cumple en \(M, q_0\) es \(\neg G pos_0 \rightarrow F pos_1\): si en algún momento punto el carro se aleja de la posición 0, debe alcanzar la posición 1.Lógica Temporal con Ramificación - CTL*
La lógica temporal lineal carece de la capacidad de distinguir entre cursos de acción necesarios y posibles cursos de acción. Dado un camino infinito particular, LTL aborda lo que sucederá. Dado un modelo de transición de Kripke, capta lo que debe suceder. Sin embargo, a veces también es importante expresar que algo puede ocurrir en al menos un camino posible. La lógica de árbol computacional (CTL*) amplía LTL con cuantificadores (duales) de camino \(E\) (*hay/existe un camino*) y \(A\) (*para cada/todo camino*). La semántica asociada a (CTL*) asociada a un modelo de transición Kripte \(M = \left\langle St, \longrightarrow, \mathcal{V} \right\rangle\) y un estado \(q\) de \(M\) se define como: - \(M,q \models p \iff q \in \mathcal{V}(p)\) - \(M,q \models \neg \varphi \iff M,q \not \models \varphi\) - \(M,q \models \varphi \wedge \psi \iff M,q \models \varphi \wedge M,q \models \psi\) - Analógamente para el resto de conectivas proposicionales. - \(M,q \models E \varphi \iff\) hay algún camino \(\lambda\) en \(M\) comenzando en \(q\), tal que \(M, \lambda \models \varphi\). - \(M,q \models A \varphi \iff\) para todo camino \(\lambda\) en \(M\) comenzando en \(q\), se tiene \(M, \lambda \models \varphi\). - La semántica CTL* asociada a las fórmulas de camino es esencialmente la presentada para la Lógica LTL. - \(M,\lambda \models p \iff M, \lambda[0] \models p \) - \(M, \lambda \models \neg \varphi \iff M, \lambda \not \models \varphi \) - \(M, \lambda \models \varphi \wedge \psi \iff M, \lambda \models \varphi \wedge M, \lambda \models \psi \) - Similar para el resto de conectivas proposicionales - \(M, \lambda \models X \varphi \iff \lambda[1...] \models \varphi \) - \(M, \lambda \models \varphi\, U \,\psi \iff \exists i \geq 0 \, | \, M, \lambda[i...] \models \psi \wedge \forall j < i : M, \lambda[j..] \models \varphi \) !!!Tip: (Ejemplo) Robots y carros II Para el modelo de transición de Kripke \(M\) presentado en el tema, tenemos por ejemplo \(M , q_0 \models E F pos_2\): en el estado \(q_0\), hay un camino tal que el carro llegará a la posición 2 en algún momento en el futuro (por ejemplo el camino \(q_0 \leadsto q_0q_1 \leadsto q_0q_1q_2\)) . Lo mismo claramente no es cierto para todos los caminos, por lo que también tenemos que \(M , q_0 \models \neg A F pos_2\). !!!Tip: (Ejemplo) Cohete Simple La figura presenta un modelo de Kripke \(M'\) para una variante sencilla del dominio del cohete que solía ser popular en la comunidad de planificación de STRIPS. Un cohete puede estar en su base en Londres (denotado por la proposición \(roL\)) o en el aeródromo de París (\(roP\)). El cohete también puede desplazarse entre los aeródromos si tiene combustible (\(fuelOK\)), pero el vuelo gasta todo el combustible y vacía el depósito de combustible (\(nofuel\)) hasta que se rellene. Una carga puede estar en la base de Londres (\(caL\)), en la base de París (\(caP\)), o dentro del cohete (\(caR\)). Cuando está fuera, puede cargarse en el cohete si están en la misma ubicación. Cuando está dentro, se puede descargar.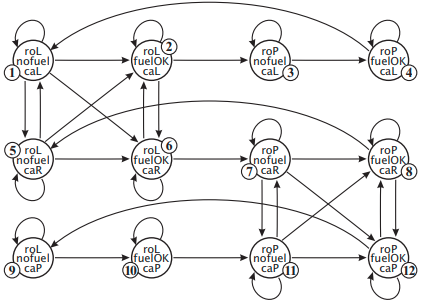
CTL Vanilla - CTL
CTL (llamado a veces CTL Vanilla o CTL sin estrella) es un sublenguaje de CTL* en el que cada ocurrencia de un cuantificador de camino va seguida inmediatamente por exactamente un operador temporal, y viceversa. Formalmente:Equivalencias de punto fijo y Cálculo Modal µ-cálculo
Fixpoint Characterization of CTL Operators
Las siguientes fórmulas son válidas en CTL, esto es, son verdaderas en todo estado de todo modelo: - \(EF\varphi \leftrightarrow \varphi \vee EX EF \varphi \) - \(EG\varphi \leftrightarrow \varphi \wedge EX EG \varphi \) - \(E\varphi_1\, U \,\varphi_2 \leftrightarrow \varphi_2 \vee ( \varphi_1 \wedge EX E \varphi_1\, U \,\varphi_2) \) - \(AF\varphi \leftrightarrow \varphi \vee AX AF \varphi \) - \(AG\varphi \leftrightarrow \varphi \wedge AX AG \varphi \) - \(A\varphi_1\, U \,\varphi_2 \leftrightarrow \varphi_2 \vee ( \varphi_1 \wedge AX A \varphi_1\, U \,\varphi_2) \) La importancia de estas equivalencias reside en el hecho de que establecen que los caminos que satisfacen las especificaciones CTL pueden construirse de forma incremental, paso a paso. Además, las soluciones al problema de verificación, así como la comprobación de la satisfacción, pueden obtenerse de forma iterativa. El punto de vista algorítmico de la computación de los estados que satisfacen una fórmula temporal puede formalizarse mediante lógicas de computación de punto fijo, es decir, variantes del cálculo modal \(\mu\)-calculus. El µ-cálculo es una extensión de la lógica modal proposicional con los operadores de punto fijo menor y mayor (\(\mu\) y \(\nu\)). La idea principal es utilizar la semántica denotativa de las oraciones modales, en la que se supone que las fórmulas denotan conjuntos de estados, y los operadores modales (unarios) se interpretan como transformadores de dichos conjuntos. Entonces, para un transformador \(\tau\) , la fórmula \(\mu Z. \tau (Z)\) se refiere al menor punto fijo de \(\tau\) , es decir, el menor conjunto de estados \(Q\) tal que \(\tau (Q) = Q\). Análogamente, \(\nu Z.\tau (Z)\) denota el mayor punto fijo de \(\tau\) , es decir, el mayor conjunto de estados \(Q\) que \(\tau(Q) = Q\). El \(\mu\)-cálculo se construye normalmente sobre operadores PDL. Aquí presentamos la variante variante más sencilla basada en los operadores CTL *nexttime*. Formalmente, sea \(\mathcal{PV}\) un conjunto de proposiciones atómicas con el elemento típico \(p\), y que \(FV\) sea un conjunto de variables de punto fijo con el elemento típico \(Z\). Los elementos de \(FV\) servirán como variables de segundo orden que actúan sobre conjuntos de estados. El lenguaje del \(\mu\)-cálculo está definido por la siguiente gramática:Lógica temporal en el marco del µ-cálculo
El µ-cálculo modal es estrictamente más expresivo que el PDL, LTL, CTL y CTL*. En particular, cada fórmula de CTL* puede traducirse al µ-cálculo. Mientras que la traducción del CTL* completo es bastante complejo, las modalidades básicas de CTL pueden traducirse a fórmulas del µ-cálculo siguiendo un esquema sencillo: - \(tr(EF\varphi) \equiv \mu Z. (tr(\varphi) \vee EX Z)\) - \(tr(EG\varphi) \equiv \nu Z. (tr(\varphi) \vee EX Z)\) - \(tr(E\varphi_1\, U \,\varphi_2) \equiv \mu Z. (tr(\varphi_2) \vee ( tr(\varphi_1) \wedge EX Z))\) - \(tr(AF\varphi) \equiv \mu Z. (tr(\varphi) \vee AX Z)\) - \(tr(AG\varphi) \equiv \nu Z. (tr(\varphi) \vee AX Z)\) - \(tr(A\varphi_1\, U \,\varphi_2) \equiv \mu Z. (tr(\varphi_2) \vee ( tr(\varphi_1) \wedge AX Z))\) Así, el \(\mu\)-cálculo modal puede considerarse una especie de *lenguaje ensamblador* para el razonamiento sobre el tiempo. Por un lado, el \(\mu\)-cálculo es más expresivo y está más cerca de los algoritmos reales. Por otro lado, las especificaciones escritas en lógicas como CTL y CTL* suelen ser mucho más legibles y expresan las propiedades temporales de forma más intuitiva.Verificación de propiedades temporales
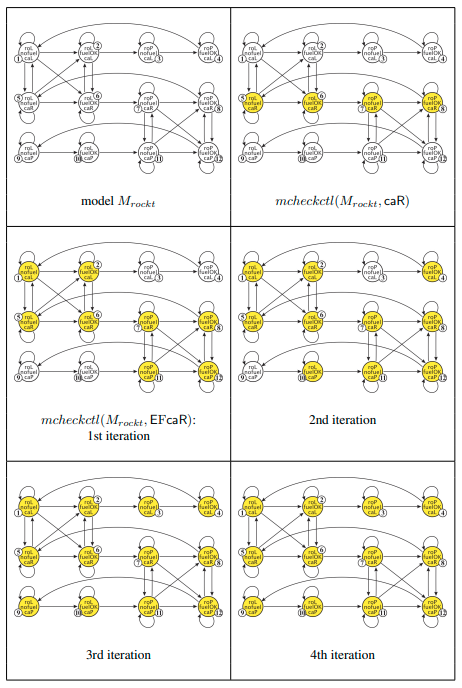
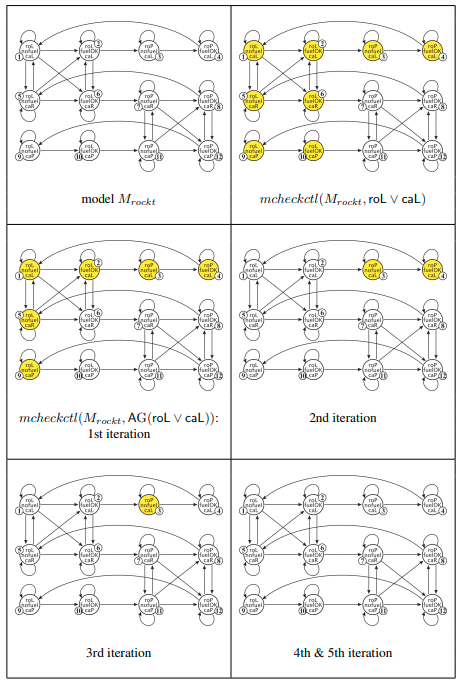
El algoritmo estándar de comprobación de modelos para CTL combina las ideas de la verificación de propiedades epistémicas, con el cálculo de puntos fijos. Es decir, la verificación de las modalidades de *un paso* se realiza calculando la preimagen adecuada, mientras que la comprobación del modelo de las propiedades a largo plazo se realiza calculando el punto fijo adecuado. Lo primero se aplica a los operadores *nexttime* \(EX\), \(AX\), mientras que el segundo constituye la columna vertebral del algoritmo para las modalidades a largo plazo \(E U\) , \(A U\) (computando el menor punto fijo) y \(E G\) , \(A G\) (computando el mayor punto fijo). Así el algoritmo quedaría como: !!!code: Función \(mcheckctl(M, \varphi)\) - \(\varphi \equiv p \implies mcheckctl(M, \varphi) = \mathcal{V(p)}\) - \(\varphi \equiv \neg psi \implies mcheckctl(M, \varphi) = St \setminus mcheckctl(M, \psi)\) - \(\varphi \equiv psi_1 \wedge \psi_2 \implies mcheckctl(M, \varphi) = mcheckctl(M, \psi_1) \cap mcheckctl(M, \psi_2)\) - \(\varphi \equiv psi_1 \vee \psi_2 \implies mcheckctl(M, \varphi) = mcheckctl(M, \psi_1) \cup mcheckctl(M, \psi_2)\) - \(\varphi \equiv EX \psi \implies mcheckctl(M, \varphi) = pre_{\exists}(mcheckctl(M, \psi))\) - \(\varphi \equiv EG \psi \implies mcheckctl(M, \varphi) = Q\). Tal que \(Q\) se obtiene de: 1. \(Q_1 = St\); \(Q_2 = mcheckctl(M, \psi)\) 2. Mientras \(Q_1 \not\subseteq Q_2\): 1. \(Q_1 \gets Q_2\) 2. \(Q_2 \gets pre_{\exists}(Q_1) \cap Q_1 \) 3. \(Q = Q_1\) - \(\varphi \equiv E\psi_1\, U \,\psi_2 \implies mcheckctl(M, \varphi) = Q\). Tal que \(Q\) se obtiene de: 1. \(Q_1 = \emptyset\); \(Q_2 = mcheckctl(M, \psi_1)\); \(Q_3 = mcheckctl(M, \psi_2)\) 2. Mientras \(Q_3 \not\subseteq Q_1\): 1. \(Q_1 \gets Q_1 \cup Q_3\) 2. \(Q_3 \gets pre_{\exists}(Q_1) \cap Q_2 \) 3. \(Q = Q_1\) - \(\varphi \equiv AX \psi \implies mcheckctl(M, \varphi) = pre_{\forall}(mcheckctl(M, \psi))\) - \(\varphi \equiv AG \psi \implies mcheckctl(M, \varphi) = Q\). Tal que \(Q\) se obtiene de: 1. \(Q_1 = St\); \(Q_2 = mcheckctl(M, \psi)\) 2. Mientras \(Q_1 \not\subseteq Q_2\): 1. \(Q_1 \gets Q_2\) 2. \(Q_2 \gets pre_{\forall}(Q_1) \cap Q_1 \) 3. \(Q = Q_1\) - \(\varphi \equiv A\psi_1\, U \,\psi_2 \implies mcheckctl(M, \varphi) = Q\). Tal que \(Q\) se obtiene de: 1. \(Q_1 = \emptyset\); \(Q_2 = mcheckctl(M, \psi_1)\); \(Q_3 = mcheckctl(M, \psi_2)\) 2. Mientras \(Q_3 \not\subseteq Q_1\): 1. \(Q_1 \gets Q_1 \cup Q_3\) 2. \(Q_3 \gets pre_{\forall}(Q_1) \cap Q_2 \) 3. \(Q = Q_1\)- \(pre_{\exists}(Q) = \{q \vert \exists q' : q \longrightarrow q' \wedge q' \in Q\}\) - \(pre_{\forall}(Q) = \{q \vert \forall q' : q \longrightarrow q' \implies q' \in Q\}\) !!!Tip: Ejemplo: Cohete Simple Consideremos el modelo de cohete simple \(M'\)La ejecución del algoritmo de comprobación de modelos CTL para la fórmula \(E F caR\), da como resultado que todos los estados de \(M'\) satisfacen la fórmula.