**SVRAI**
Espacios de Estados
Representación y Búsquedas
Sin lugar a dudas, una de las principales características que reconocemos en la inteligencia es la capacidad para resolver problemas. Si consideramos una inteligencia como la humana, a la habilidad para analizar los elementos intrínsecos de cada problema, que está presente también en muchas otras especies animales, se añade la **capacidad de abstraerlos e identificar las acciones que se pueden realizar** sobre ellos para resolver el problema. En un nivel incluso superior de abstracción, reconocible solo en las llamadas especies superiores, podemos considerar también la capacidad de determinar cuál puede ser, de entre los posibles métodos que se idean, el más adecuado, ya sea en términos de tiempo, de recursos, de seguridad para el individuo, etc. De esta forma, aparece una triple capacidad de **análisis**, **abstracción** y **estrategia** que sitúa el tema general de la resolución de problemas en el núcleo de la inteligencia artificial y, por ello, no resulta extraño que se consideren deseables para cualquier individuo, artificial o no, que queramos que se comporte inteligentemente.
Podemos pensar en una variedad de problemas que van desde cómo alcanzar una fuente de comida situada a cierta distancia y a la que no se puede ir directamente, hasta cómo resolver un pequeño juego como podría ser el famoso cubo de Rubik, o resolver el problema matemático de encontrar la solución a una ecuación numérica. En todos ellos encontramos elementos comunes tras un proceso de abstracción que nos permiten de forma general definir la **resolución de problemas** como:
!!!def
El proceso que, partiendo de una situación inicial y utilizando un conjunto de procedimientos/acciones/acciones seleccionados a priori, es capaz de explicitar el conjunto de pasos que nos llevan a una situación posterior que llamamos **solución**.
Lo que consideremos o no solución dependerá del contexto concreto del problema, y puede ser, por ejemplo, el conjunto de acciones que nos llevan a cumplir cierta propiedad, conseguir cierto objetivo, o verificar ciertas restricciones.
Como estamos interesados en la generación de mecanismos automáticos que se puedan llamar inteligentes, no nos contentamos con resolver problemas individuales y dar para cada problema una solución independiente, sino que intentaremos buscar elementos comunes a una gran bolsa de problemas que faciliten dar una clasificación de los mismos y reconocer métodos y estrategias que puedan ser válidos de la forma más general posible.
Para ello, y teniendo en cuenta lo la idea de **modelar**, es necesario que podamos expresar las características de los problemas usando un lenguaje formal común a todos ellos, para posteriormente proporcionar métodos y estrategias generales (en forma de algoritmos o de heurísticas, en nuestro caso) con los que poder obtener con ciertas garantías soluciones de esos problemas.
Una de las aproximaciones más generales y sencillas de formalizar un problema y sus posibles mecanismos de solución es por medio de lo que se denomina **espacio de estados**. Antes de definir formalmente en qué consiste este espacio, observemos que en todo momento estamos tratando con métodos en los que la resolución de los problemas se dan de forma dinámica, es decir, se supone que se produce una evolución temporal, que pasa por etapas, que nos permite llegar de la situación inicial en la que el problema se presenta hasta una situación final en la que se ha encontrado la solución del mismo. Es precisamente esta dinámica, en la que aplicamos las acciones u operaciones de las que disponemos, la que permite ir modificando cada situación posible para llevarnos desde el inicio a la solución. Simplemente, denominaremos **estado** a la *representación de los elementos que describen el problema en un momento dado*, es decir, a la situación en que se encuentra o se podría encontrar el problema en cada instante de tiempo.
!!!def: Estado
Representación de los elementos que describen el problema en un momento dado.
La cuestión principal que debemos plantearnos para esta metodología es acerca de qué debemos incluir en el estado. Por desgracia, no existen directrices generales que permitan dar una respuesta satisfactoria a esta cuestión pero, siguiendo técnicas de resolución de problemas clásicas, podemos asegurar que es importante guardar un equilibrio entre el ahorro de recursos de almacenamiento para la descripción del estado y la necesidad de tener suficiente información almacenada como para poder resolver el problema. Aunque a priori puede parecer una buena idea almacenar toda la información posible, pronto veremos que en problemas relativamente pequeños la cantidad de estados puede ser tan grande que la capacidad de almacenamiento computacional se nos puede agotar sin darnos la opción de resolver el problema. Vemos, pues, que este enfoque entronca directamente con teorías matemáticas bien establecidas, como son la **Teoría de la Computabilidad** (que estudia qué es resoluble de forma automática) y la **Teoría de la Complejidad** (que estudia cuántos recursos necesitamos para resolver los problemas que sí son resolubles).
!!!note
Debe existir un equilibrio entre el ahorro de recursos de almacenamiento para la descripción del estado y la necesidad de tener suficiente información almacenada como para poder resolver el problema
Este proceso de elegir adecuadamente la información que almacenamos en un estado es tan importante que se ha convertido en un eje central de la Inteligencia Artificial, recibiendo el nombre de **Teoría de la Representación**, y ha demostrado ser esencial para que algoritmos y heurísticas concretas de resolución sean o no eficientes a la hora de resolver problemas. Un buen algoritmo con una mala representación puede ser tan ineficiente como un mal algoritmo y, muchas veces, una buena representación es capaz de llevarnos a una solución del problema incluso usando algoritmos malos.
!!!note
La elección de los estados no solo determina qué información se almacenará de las diversas situaciones por las que pasa el problema, sino que en muchos casos es determinante también para decidir cuáles son las acciones u operaciones básicas que se permiten para realizar transformaciones entre estados.
Otras veces también podemos encontrar restricciones debido a la incapacidad para realizar ciertas acciones para resolver un problema, lo que puede influir en cómo se elegirán los estados para hacerlos coherentes con las operaciones disponibles. En general, el proceso de transformar el problema original (al que muchas veces llamaremos simplemente *mundo real*) en este espacio de estados que es manipulable por medios automáticos es lo que conocemos como **modelar el problema** (debe tenerse en cuenta que el modelado existe en otras muchas ramas de la ciencia, y nosotros aquí solo consideramos el modelado computacional, que es un tipo particular de modelado matemático).
!!!def
Modelar computacional de un problema: proceso de transformar el problema original (*mundo real*) en un espacio de estados que es manipulable por medios automáticos.
# Problema de búsqueda básico
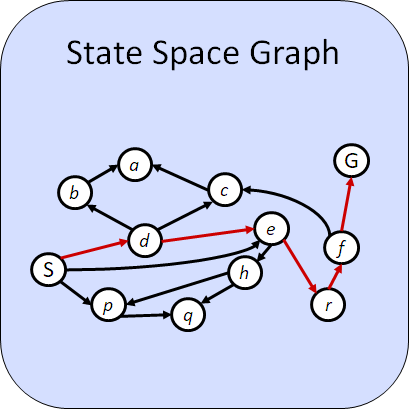
Si nos imaginamos este espacio de estados como un terreno por el cual nos podemos mover, donde partimos de un punto concreto del terreno (**estado inicial**) y podemos aplicar las acciones válidas para ir saltando de un estado a otro, podemos identificar la resolución del problema (llegar hasta un **estado final** válido) con el problema de **buscar un camino** adecuado entre un estado inicial y un estado final. Es por ello que muy habitualmente se habla del **Problema de Búsqueda en el Espacio de Estados**. Pasemos pues a dar una definición formal de esta idea:
!!!def:Problema de Búsqueda Básico
Un **problema de búsqueda básico** es una 4-tupla $(X,S,G,T)$, donde:
- $X$ es un conjunto de **estados** (**Espacio de Estados**).
- $S \subseteq X$, es un conjunto no vacío de **estados iniciales**.
- $G \subseteq X$, es un conjunto no vacío de **estados finales**.
- $T: X \rightarrow \cal{P}(X)$ es una **función de transición**. Para cada $x\in X$, $T(x)$ determina el conjunto de estados sucesores de $x$.
Debemos considerar los siguientes hechos:
1. $\cal{P}(X)$ representa al conjunto **partes de $X$** (o conjunto **potencia de $X$**), es decir, el conjunto de los posibles subconjuntos de $X$, ya que desde un estado concreto podemos llegar a varios posibles estados aplicando distintas operaciones o acciones permitidas.
2. Muchas veces $G$ no se da explícitamente, sino por medio de las propiedades que verifican los estados para ser considerados finales.
3. En algunos contextos (como el que veremos el resto del curso) las transiciones se denominan **acciones**, y para cada $s \in X$ se denota por $\mathscr{A}(s)$ al conjunto de acciones/transiciones aplicables al estado $s$. En este caso, es común reservar $T$ para la aplicación de la acción, es decir: $T(s,a)$ es el estado que se obtiene de aplicar la acción $a$ sobre el estado $s$.
3. En la definición anterior no se explicita ni la forma en que hay que almacenar la información en los estados, ni cuáles son las acciones válidas que permiten pasar de un estado a otro durante la resolución, ya que esto depende del problema concreto que se esté resolviendo y nosotros estamos interesados en dar un marco general que permita aplicar los métodos que desarrollemos al mayor conjunto posible de problemas.
!!!note
Una vez fijado este primer marco de representación, podemos dar los pasos generales necesarios para *buscar* un camino que lleve desde el planteamiento inicial del problema hasta una solución:
1. **Dar una representación del problema**, es decir, definir un **espacio de estados** que refleje las características del mundo real que sean necesarias para la resolución del problema. Como ya se ha indicado, ha de tenerse en cuenta que esta elección no es única, y que determinará en gran medida la facilidad o dificultad de resolver el problema que tenemos entre manos. Además, este paso determina también las acciones disponibles para moverse por este espacio.
2. Especificar los **estados iniciales**.
3. Especificar los **estados finales** (objetivos o metas). A veces no se especifican propiamente los estados finales, sino alguna propiedad que han de cumplir para que se consideren válidos.
4. Definir **acciones** a partir de las transiciones disponibles. El conjunto de acciones definirá la función de transición del sistema formal. Las acciones aportan una **estructura al espacio de estados**, que será responsable, en gran medida, de la dificultad que nos encontremos posteriormente para realizar búsquedas en el espacio.
5. El problema se resuelve **usando las acciones en combinación con una estrategia de control**. De nuevo, aquí no prefijaremos ninguna estrategia de control específica.
6. Dependiendo de la estrategia de control utilizada, o de las necesidades de la búsqueda, puede ser necesaria una **función de coste** que indique cuánto cuesta aplicar una acción determinada a un estado determinado, de esa forma podemos calcular cuánto cuesta el proceso total de ir desde un estado inicial hasta un estado final aplicando dicha estrategia, y de esta forma comparar entre sí los distintos caminos que existen para resolver el problema.

## Planificación
!!!def
En muchos casos no estamos interesados *simplemente* en encontrar un estado final que verifique ciertas propiedades, sino en encontrar la sucesión de acciones que llevan desde un estado inicial particular hasta un estado final deseado. En este caso estamos ante lo que se conoce como un **Problema de Planificación**, y a la sucesión concreta de acciones que resuelve el problema se le denomina **plan**.
Este tipo de problemas tiene muchas aplicaciones en el mundo real, que van desde la robótica hasta la generación de planes para la automatización de cadenas de montaje pasando, por supuesto, en la resolución de juegos.
Aunque se suele relacionar con los **Problemas de Scheduling**, donde también se busca una sucesión de acciones ordenadas temporalmente, hay una diferencia principal, y es que en este caso el énfasis se pone en la optimización de recursos que usan las acciones que intervienen.
## Ejemplos
Como primer ejemplo, consideremos el **puzzle de piezas deslizantes**, donde el objetivo es deslizar las piezas usando el hueco hasta conseguir el orden deseado. El caso general consiste en un puzzle de $n\times m$ cuadrículas, con $n\times m-1$ piezas numeradas consecutivamente y 1 hueco. A veces podemos encontrar este puzzle en una variante equivalente haciendo uso de imágenes que han de reconstruirse situando el orden adecuado en sus piezas.

El espacio de estados, $X$, describe todas las posibles combinaciones de las piezas y el hueco. Como queremos dar un método general de resolución, el conjunto de los estados iniciales es, en este caso, todo el espacio $S=X$, y el conjunto de estados finales es únicamente uno, el estado en el que todos están en orden y el hueco se sitúa al final, tal y como muestra la figura anterior. La función de transición describe el cambio que resulta de mover, en un estado concreto, el hueco en cualquiera de las 4 direcciones (en los bordes y esquinas sólo podrá moverse en 3 o 2 direcciones posibles, respectivamente).
Obsérvese que, en este caso, la solución al puzzle no es el estado final, que sabemos exactamente cuál es, sino el camino que lleva desde un estado inicial (prefijado, o aleatorio) hasta ese estado final. Es decir, deseamos conocer la sucesión de movimientos que nos permiten resolver el puzzle.
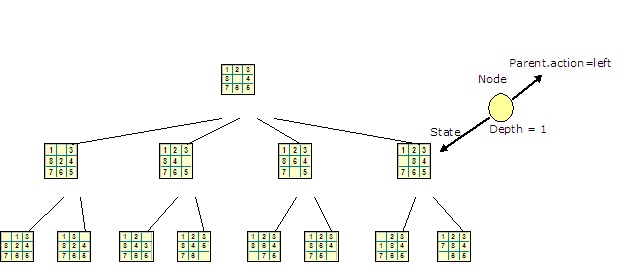
En el caso de un puzzle de tamaño $3\times 3$ (en este caso el puzzle se conoce como **8-puzzle**, que es el número de piezas móviles) el número de posibles estados es de $9!= 362880$, un tamaño que permite, con la capacidad de los ordenadores actuales, hacer una búsqueda exhaustiva para encontrar el camino desde cualquier estado al estado final ordenado. Esta búsqueda exhaustiva se consigue comenzando por el estado inicial e ir visitando a partir de él todos los demás estados por la aplicación sucesiva de las acciones de transición, de esta forma, si existe una solución (un camino que conecta el estado inicial y el final) este método la encontrará, aunque, posiblemente, de una forma completamente ineficiente.
Si jugamos con el puzzle de tamaño $4\times 4$ (que se conoce como **15-puzzle**) el número de posibles estados es de $16! \approx 2x10^{13}$, demasiado grande para una búsqueda exhaustiva. En casos como éste, donde el espacio de estados es excesivamente grande para hacer un recorrido exhaustivo de sus elementos, hemos de encontrar estrategias de búsqueda más depuradas que nos permitan alcanzar las soluciones de forma más eficiente y usando menos recursos (en tiempo y en espacio almacenado).
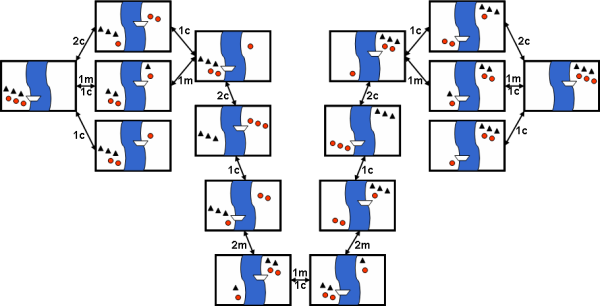
Consideremos otro puzzle habitual, **el puzzle de los misioneros y caníbales**: Tres misioneros se perdieron explorando una jungla. Separados de sus compañeros, sin alimento y sin radio, sólo sabían que para llegar a su destino debían ir siempre hacia adelante. Los tres misioneros se detuvieron frente a un río que les bloqueaba el paso, preguntándose que podían hacer. De repente, aparecieron tres caníbales llevando un bote, pues también ellos querían cruzar el río. Ya anteriormente se habían encontrado grupos de misioneros y caníbales, y cada uno respetaba a los otros, pero sin confiar entre ellos. Los caníbales se comían a los misioneros cuando les superaban en número, y los misioneros bautizaban a los caníbales en situaciones similares. Todos querían cruzar el río, pero el bote no podía llevar más de dos personas a la vez y los misioneros no querían que los caníbales les aventajaran en número. ¿Cómo puede resolverse el problema, sin que en ningún momento hayan más caníbales que misioneros en cualquier orilla del río?
El espacio de estados asociado al problema podría representarse de la siguiente forma (muy descriptiva, pero poco práctica desde el punto de vista computacional):
# Criterios de evaluación
Antes de que pasemos a ver la variedad de algoritmos (estrategias) que han sido diseñados para resolver problemas de búsqueda en espacios de estados, puede merecer la pena mencionar, aunque sea de forma breve, cómo podemos evaluar la eficiencia de estos algoritmos.
!!!note
Habitualmente, se suelen usar los siguientes criterios de evaluación:
- **Complejidad en tiempo**: Se puede medir como el número de veces que se aplica la función de transición que necesita el algoritmo para encontrar la solución. En un contexto más amplio suele medirse por medio del número de pasos que da un algoritmo en su ejecución.
- **Complejidad en espacio**: Se mide por la cantidad de espacio de almacenamiento necesario para encontrar la solución. En el caso que estamos viendo lo podemos medir como el número de estados que el algoritmo debe mantener en memoria para encontrar la solución. Algunos algoritmos podrán "olvidar" los estados por los que van pasando, mientras que otros necesitan mantener una memoria con esos estados para poder volver atrás en la búsqueda o saber por cuáles ha pasado.
- **Completitud**: Si existe una solución, ¿está garantizado por el algoritmo que la encontraremos?
- **Optimalidad**: Si existen varias soluciones, ¿encuentra el algoritmo la óptima? Esta optimalidad se mide respecto de alguna medida, por ejemplo, la que requiere menor número de acciones para llegar desde el estado inicial, o la que usa menos memoria.
# Una representación (casi) universal
Normalmente, los algoritmos que vamos a ver se basan en la suposición de que el espacio de búsqueda tiene la estructura de un grafo dirigido: cada **nodo** del grafo representa uno de los estados del espacio, y dos nodos están conectados si existe una forma de ir de uno al otro por medio de una acción.
Normalmente, cuando resolvemos el problema a partir de un estado particular, podemos construir un árbol que se construye partiendo del estado inicial y donde en cada nivel se añaden los estados que se pueden alcanzar desde los estados del nivel anterior (y que, en consecuencia, puede contener estados repetidos). En este caso, la **profundidad** ($d$, de **depth**) del árbol es la longitud máxima de los caminos que se pueden construir desde cualquier nodo a la raíz; y el **factor de ramificación** ($b$, de **branch**) del árbol es el máximo número de sucesores que puede tener un nodo del árbol.
En un árbol, los sucesores inmediatos de un nodo (salvo las **hojas**, claro, que son los nodos terminales) se llaman **hijos**, el predecesor de un nodo (salvo la **raíz**, que no tiene predecesor), que es único, se llama **padre**, y los nodos que tienen el padre común se llaman **hermanos**.
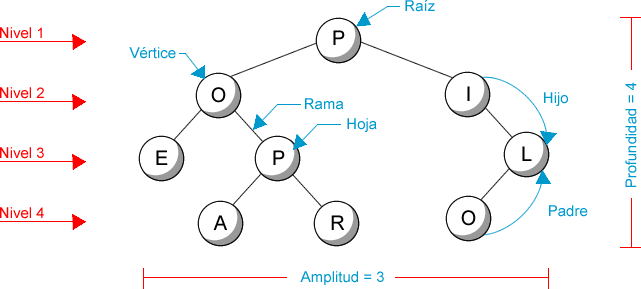
Es importante destacar que nuestro espacio de estados **NO** es un árbol, sino que el árbol se consigue al considerar la estructura ordenada que surge entre los diversos estados de nuestro problema al aplicar las acciones que permiten pasar de unos estados a otros. Si cambiamos la representación de los estados (y en consecuencia las acciones que se pueden aplicar) cambiará el árbol asociado, pero nuestro problema sigue siendo el mismo. Es por ello que la representación es fundamental para obtener soluciones más o menos eficientes, ya que los posibles caminos entre los nodos que representan estados iniciales y los nodos que representan estados finales pueden cambiar completamente dependiendo del árbol que obtengamos.
# Estructuras en Espacios de Estados
Hemos visto que para representar un problema como una búsqueda en un Espacio de Estados necesitamos los siguientes elementos:
1. Conjunto de Estados: $X$.
1. Estado inicial: $s_0\in X$.
1. Estados finales: $G\subseteq X$.
1. Función de transición (acciones): $T:X\to \cal{P}(X)$.
Las transiciones aportan una **estructura interna** al espacio completo de estados, $X$, que lo convierte en un espacio conectado, donde tiene sentido plantearse si hay caminos que conecten $s_0$ con $G$ y, en caso afirmativo, intentar construir el camino más *deseable* (óptimo, desde algún punto de vista). Aunque a veces $T$ viene dado con el problema, muchas veces determinar el par $(X,T)$ es parte de la **representación del problema**.
En cierta forma, el par $(X,T)$ se comportaría como un **espacio topológico**, en donde las conexiones entre estados por medio de transiciones están definiendo una relación de conectividad que configura el espacio de una cierta forma: si cambiamos las transiciones disponibles, la forma del espacio cambia. Como hemos comentado, la elección adecuada de $X$ y de $T$ puede modificar sensiblemente la resolubilidad del problema original.
!!!note: Problemas representables
El tipo de problemas que se puede resolver con esta representación es variado, dependiendo de los requerimientos adicionales (no excluyentes entre sí) que consideremos para dar una solución:
* Si solo indicamos si existe un camino, pero no especificamos cuál, estamos resolviendo un **problema de decisión**.
* Si $G$ viene dado por un conjunto de propiedades que deben verificarse en los estados alcanzados, entonces el problema se podría ver como un **problema de satisfacción de restricciones**.
* Si, además, proporcionamos un estado de $G$ al que podemos llegar desde $s_0$, estamos resolviendo un **problema de construcción**.
* Si, por encima de las dos anteriores, además estamos dando el conjunto de transiciones/acciones que llevarían desde $s_0$ a un elemento de $G$, estamos resolviendo un **problema de planificación**.
* Si en cualquiera de los problemas anteriores preferimos dar uno de los caminos o estados finales que verifique propiedades adicionales de optimalidad, entonces al problema de búsqueda le añadimos un **problema de optimización**.
## Construcción de $T^n(s_0)\subseteq X$
Lo más habitual es no disponer de $X$ de forma explícita y completa al principio de la búsqueda, sino que hemos de ir construyéndolo/descubriéndolo a partir de $s_0$ por aplicación sucesiva de elementos de $T$. Grosso modo, cuando $T$ se puede expresar como un conjunto finito de aplicaciones, $T=\{t_1,\dots,t_n\}$, esta construcción la podemos ver como un proceso iterativo en el que, partiendo de $s_0$, construimos por niveles los estados que podemos alcanzar por aplicación de los elementos de $T$:
$$\{s_0\}$$
$$\{s_1=t_1(s_0),\dots,s_n=t_n(s_0)\}$$
$$\{s_{11}=t_1(s_1),\dots,s_{1n}=t_n(s_1),\dots,s_{n1}=t_1(s_n),\dots,t_{nn}=t_n(s_n)\}$$
$$\vdots$$
En general, para cualesquiera $\{i_1, \dots, i_k, i_{k+1}\}\subseteq \{1,\dots,n\}$ podríamos considerar:
$$s_{i_1\dots i_k i_{k+1}}=t_{i_{k+1}}(s_{i_1\dots i_k})=t_{i_{k+1}}\circ \cdots \circ t_{i_1}(s_0)$$
donde $f\circ g$ representa la composición de aplicaciones: $f\circ g(x)=f(g(x))$.
Si el espacio $(X,T)$ es fuertemente conexo (es decir, desde cualquier estado puedo conseguir cualquier otro por aplicación sucesiva de acciones de $T$), entonces el problema de búsqueda tendrá solución, independientemente de $s_0$ y $G$, es decir, que sabemos que hay, al menos, una sucesión de acciones que conecta $s_0$ con una solución. Muchas veces la situación no es esa, y entonces dependerá de $T$ para que, al menos, podamos alcanzar algún elemento de $G$ desde un $s_0$ concreto.
Además, en caso de que sí sea alcanzable, puede haber más de un camino que lleve a un estado final, pudiendo variar de un camino a otro en el orden de aplicación de las transiciones que se han aplicado, en la longitud de la cadena de transiciones aplicadas, o en las propiedades que verifiquen las transiciones elegidas (por ejemplo, si son conmutativas, $t_i\circ t_j=t_j\circ t_i$, asociativas, $t_i\circ (t_j\circ t_k)=(t_i\circ t_j)\circ t_k$, etc.), entre otras muchas. Conocer a priori las propiedades que verifica $T$ puede simplificar la generación de los estados de $X$, ya que puede evitar la creación de estados repetidos innecesariamente o de caminos esencialmente equivalentes (o de caminos indeseables).
Partiendo de esta visión iterada de cómo construir elementos de $X$, podemos dar las funciones necesarias para hacerlo de forma compacta en un lenguaje cualquiera con una mínima estructura funcional.
# Una implementación sencilla
Vamos a suponer que tenemos $T$ en forma de colección de funciones que realizan las diferentes acciones/transiciones. Al conjunto de acciones aplicables del estado $s$ lo notaremos por $T_s=A(s)\subseteq T$.
Podemos definir la función que calcula los sucesores como:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
function T(s) := {t(s) : t ∈ A(s)}
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Por lo que la construcción a partir de $s_0$ quedaría como:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
function Generate-X-from(s₀) :=
X = Fr = {s₀}
while (Fr ⋂ G = ∅)
Fr = ⋃ {T(s) : s ∈ Fr}
X = X ⋃ Fr
return X
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Vemos que la generación de $X$ (hasta que encontremos algún elemento de $G$) es realmente directa gracias a la aproximación funcional:
1. Partiendo de la frontera inicial: $Fr=\{s_0\}$.
2. Construimos los sucesores de $Fr$ por la aplicación de todas las transiciones disponibles a todos los elementos de la frontera.
3. Acumulamos $Fr$ en $X$ (para no perder los estados obtenidos).
4. Si en $Fr$ no hay elementos de $G$, repetimos desde el paso 2. En caso contrario, devolvemos $X$.
Trabajar con la frontera ayuda a no estar calculando continuamente los sucesores de estados por los que ya hemos pasado en etapas anteriores (esto no asegura no tener repetidos, pero al menos no repite el mismo proceso una y otra vez sobre todos los elementos).
Aunque así se ha simplificado mucho el proceso, lo más común es trabajar con una versión *relajada* de las acciones que facilita la creación del espacio, y es probable que haya elementos representables que no se correspondan con estados válidos (por ejemplo, una representación de estados como números, pero donde solo tengan sentido los números positivos). Para tener en cuenta estas limitaciones, es posible tomar dos estrategias:
1. **Restringir $T$**: Las transiciones de $T$ solo generan estados válidos.
2. **Validar $T$**: Tras generar posibles estados por elementos de $T$, se desechan aquellos que no son válidos.
Cuando las características de los estados están claras, la implementación de la segunda estrategia es directa (apenas un pequeño cambio) y facilita la construcción de $T$ desde el punto de vista de la programación. Para ello, supondremos que existe un predicado, `valid?`, que indica si un estado es válido o no (o, mejor dicho, si una representación realmente es un estado). Con este predicado basta cambiar la función que calcula los sucesores de la siguiente forma:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
function T(s) := {t(s) : t ∈ T ∧ valid?(t(s))}
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
No es necesario cambiar nada de los demás procedimientos, porque la generación de sucesores se ha restringido para devolver solo estados válidos.
Sin embargo, todavía se puede mejorar el proceso de generación eliminando los estados repetidos:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
function Generate-X-from(s₀) :=
X = Fr = {s₀}
while (Fr ⋂ G = ∅)
Fr = ⋃ {T(s) : s ∈ Fr}
Fr = remove-duplicates (Fr \ X)
X = X ⋃ Fr
return X
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# Generación Selectiva
Desde un punto de vista computacional, la generación anterior tiene muchas deficiencias. Aunque va generando todos los estados de $X$ que se pueden obtener a partir de $s_0$, no es un mecanismo que se pueda ofrecer como solución a problemas de búsqueda porque tiene muchas opciones de explotar exponencialmente (tanto en memoria, es decir, número de estados que van apareciendo, como en tiempo, por el número de aplicaciones de $T$ que se aplican en cada paso) en cuanto la media de transiciones aplicables desde cada estado sea mayor que $1$. Además, muchísimos de los estados generados en el proceso no tendrán ningún valor para la solución de la búsqueda.
Por ello, los algoritmos de búsqueda implementan **estrategias** que permiten recorrer/generar $X$ haciendo la expansión de un solo estado en cada paso, con el fin de controlar la complejidad del proceso de generación e intentar introducir algo de *inteligencia* en el proceso de selección.
La forma general de un proceso de búsqueda que usa **selección de estados** para expandir $X$ se puede obtener muy fácilmente a partir del algoritmo anterior:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
function Selected-Search-from(s₀) :=
X = Fr = {s₀}
while (Fr ⋂ G = ∅)
sel-s = select(Fr)
Fr = T(sel-s) ⋃ (Fr \ {sel-s})
Fr = remove-duplicates (Fr \ X)
X = X ⋃ Fr
return X
end
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
donde `select` sería la estrategia: una función que selecciona, de entre los estados de la frontera que podemos expandir, el estado concreto que vamos a expandir en este paso.
Si, por ejemplo, se toma:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
function select(C)= one-of C
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
el resultado será una **búsqueda aleatoria** (`one-of` devuelve un elemento al azar de una colección).
## Búsqueda Ciega: Generación sin información
Si `T` es una lista ordenada, su orden induce un orden de aparición de los estados durante la generación de $X$. Si no se dispone de información acerca de cómo construir una estrategia que acelere el proceso de búsqueda (lo que se denomina una **búsqueda ciega**) se podría usar el orden impuesto por `Tr` para recorrer $X$ de manera ordenada.
Por ejemplo, para seguir ordenadamente cada nivel de la estructura de $X$ que se genera desde $s_0$, bastaría con ir seleccionando de la frontera el primer estado disponible y añadir los estados que se generan desde él a la cola de la frontera (en programación, es lo mismo que usar una estructura de tipo FIFO), y entonces la búsqueda se conoce como **búsqueda en anchura** (BFS, por sus siglas en inglés). Concretamente, la selección usada sería:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
function BFS-from(s₀) :=
X = Fr = [s₀]
while (Fr ⋂ G = ∅)
sel-s = select-BFS(Fr)
Fr = tail(Fr) ++ T(sel-s)
Fr = remove-duplicates (Fr \ X)
X = X ⋃ Fr
return X
end
function select-BFS := head
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Si se quiere que la **búsqueda sea en profundidad** (DFS, por sus siglas en inglés) se puede seguir seleccionando el primer estado de la frontera, pero ahora se añaden los estados que se generan desde él a la cabeza de la frontera (se construye una estructura de tipo FILO):
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
function DFS-from(s₀) :=
X = Fr = [s₀]
while (Fr ⋂ G = ∅)
sel-s = select-DFS(Fr)
Fr = T(sel-s) ++ tail(Fr)
Fr = remove-duplicates (Fr \ X)
X = X ⋃ Fr
return X
end
function select-DFS := head
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
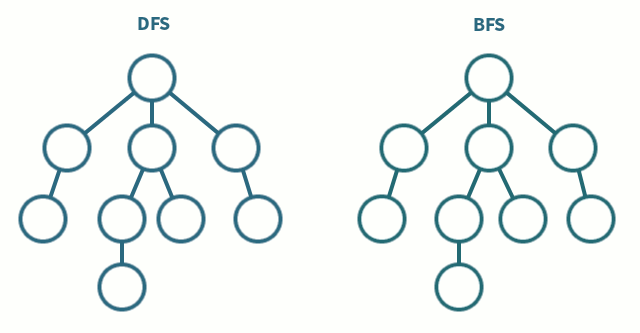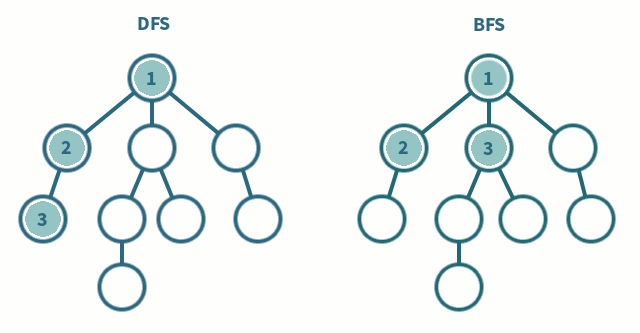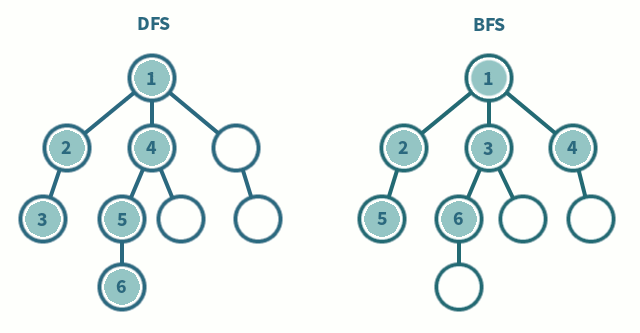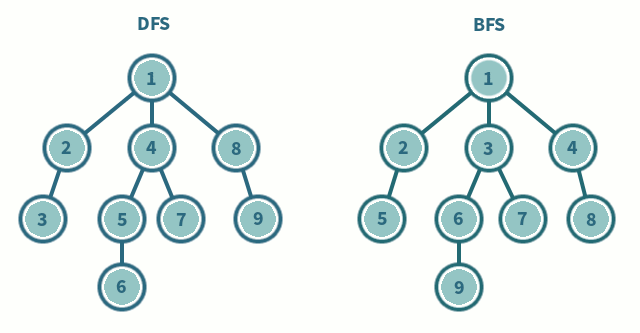
En los procedimientos anteriores, si `x=[x₁,...,xₙ]` denota una lista (sucesión ordenada de objetos), `head(x)=x₁`, y `tail(x)=[x₂,...,xₙ]`. Si además `y=[y₁,...,yₖ]`, entonces `x++y=[x₁,...,xₙ,y₁,...,yₖ]` es la concatenación de listas.
## Búsqueda Informada: Generación con información
Si la estrategia de selección es muy eficiente, la búsqueda será más rápida porque no generará una sección muy grande de $X$ para poder resolver el problema.
Normalmente, la dificultad al resolver un problema de búsqueda no se encuentra en verificar las condiciones de $G$ ni en la aplicación de los elementos de $T$, sino en la cantidad de estados adicionales que hay que generar para poder encontrar una solución, así que es normal que muchos de los esfuerzos en la resolución de problemas de búsqueda vayan orientados a reconocer propiedades adicionales de la estructura de $X$ que sirvan para definir estrategias más eficientes. Los algoritmos de búsqueda que usan este tipo de estrategias se dice que realizan una **búsqueda informada**, y uno de sus representantes más claros es el **algoritmo $A^∗$**, en el que la estrategia de búsqueda intenta minimizar el coste del camino recorrido:
!!!def
Cuando la aplicación de cada transición lleva aparejado un coste, o lo que es lo mismo, la estructura $(X,T)$ se puede representar como un grafo ponderado, en el que la transición que lleva $s$ a $s′$ se representa como una arista dirigida $(s\to s′)$ con un peso predeterminado y conocido, el algoritmo $A^∗$ calcula el camino de menor peso entre $s_0$ y un elemento de $G$ considerando que la estrategia en cada paso selecciona el nodo de la frontera que minimiza:
$$g(s)=coste(s)+h^∗(s)$$
donde $coste(s)$ es el coste real del camino que se ha construido desde $s_0$ hasta $s$, y $h^∗(s)$ es una estimación del coste mínimo que habría desde $s$ hasta $G$.
$h^∗$ se conoce como **función heurística**, y suele ser desconocida, por lo que se usan aproximaciones que podemos calcular (que denotaremos por $h$). Para asegurar que esta estrategia realmente devuelve el camino de coste mínimo usando estas aproximaciones, éstas deben verificar algunas propiedades adicionales.
En código:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
function select-A*(C) = arg_min {coste(s) + h(s) : s ∈ C}
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
donde `arg_min(f,C)` devuelve el elemento de `C` donde `f` alcanza el menor valor (de entre los de `C`).

### Condiciones para la optimalidad
Hasta ahora no hemos hablado de cómo garantizar la optimalidad de la solución. Es claro que, en el caso degenerado ($h=0$), tenemos una búsqueda en anchura guiada por el coste del camino explorado, lo que garantiza el óptimo aunque a costa de un mayor tiempo de búsqueda. Pero, como hemos comentado, la función $h$ permite introducir un comportamiento de búsqueda en profundidad, donde sabemos que no se garantiza el óptimo, pero a cambio podemos realizar la búsqueda en menor tiempo porque podemos evitar explorar ciertos caminos.
Para saber si encontraremos o no el óptimo mediante el algoritmo $A^∗$ hemos de analizar las propiedades de la función heurística.
La propiedad clave que garantizará hallar la solución óptima es la que denominaremos **admisibilidad**:
!!!def: Admisibilidad
Diremos que una función heurística $h$ es **admisible** cuando su valor en cada nodo sea menor o igual que el valor del coste real del camino que falta por recorrer hasta una solución, es decir:
$$\forall n\ (0\leq h(n)\leq h^∗(n))$$
Esto quiere decir que la función heurística ha de ser un **estimador optimista** del coste que falta para llegar a una solución. Esta propiedad implica que, si podemos demostrar que la función de estimación $h$ que utilizamos en nuestro problema la cumple, siempre encontraremos una solución óptima. El problema radica en hacer esa demostración, pues cada problema es diferente.
La **consistencia** se puede ver como una extensión de la admisibilidad. A partir de la admisibilidad se deduce que si tenemos los costes heurísticos $h^∗(n_i)$ y $h^∗(n_j)$, y el coste óptimo para ir de $n_i$ a $n_j$, $K(n_i,n_j)$, se ha de cumplir la desigualdad triangular:
$$h^∗(n_i)\leq h^∗(n_j)+K(n_i,n_j)\quad (\mbox{o, equivalentemente, }h^∗(n_i)- h^∗(n_j)\leq K(n_i,n_j))$$
La consistencia exige pedir lo mismo al estimador $h$.
!!!def:Consistencia
Un heurístico $h$ se dice **consistente** si para cualquier par de nodos $n_i$, $n_j$ verifica que:
$$h(n_i)−h(n_j)\leq K(n_i,n_j)$$
Es decir, que la diferencia de las estimaciones sea menor o igual que la distancia óptima entre nodos. Que esta propiedad se cumpla quiere decir que $h$ es un **estimador uniforme** de $h^∗$. Es decir, la estimación de la distancia que calcula $h$ disminuye de manera uniforme.
Si $h$ es consistente además se cumple que el valor de $g(n)$ para cualquier nodo es $g^∗(n)$ (es decir, el mínimo), por lo tanto, una vez hemos llegado a un nodo sabemos que hemos llegado a él por el camino óptimo desde el nodo inicial. Si esto es así, no es posible encontrar el mismo nodo por un camino alternativo con un coste menor y esto hace que el tratamiento de nodos cerrados duplicados sea innecesario, lo que ahorra tener que almacenarlos.
Suele ser un resultado habitual que las funciones heurísticas admisibles sean consistentes y, de hecho, hay que esforzarse bastante para conseguir que no sea así.
Otra propiedad interesante es la que permite comparar heurísticas entre sí, y poder saber cuál hará que $A^∗$ necesite explorar más nodos para encontrar una solución óptima:
!!!def:Heurísticos más informados
Se dice que el heurístico $h_1$ es **más informado** que el heurístico $h_2$ si se cumple la propiedad:
$$\forall n\ (0\leq h_2(n) < h_1(n)\leq h^∗(n))$$
En particular, poder verificar esta propiedad implica que los dos heurísticos son admisibles.
Si un heurístico es más informado que otro, al hacer uso de él en el algoritmo $A^∗$ se expandirán menos nodos durante la búsqueda, ya que su comportamiento será más en profundidad y habrá ciertos nodos que no se explorarán.
!!!Tip
Esto podría hacer pensar que siempre hay que escoger el heurístico más informado, pero se ha de tener en cuenta que la función heurística también tiene un tiempo de cálculo que afecta al tiempo de cada iteración, y que suele ser más costoso cuanto más informado sea el heurístico. Podemos imaginar por ejemplo que, si tenemos un heurístico que necesita $10$ iteraciones para llegar a la solución, pero tiene un coste de 100 unidades de tiempo por iteración, tardará más en llegar a la solución que otro heurístico que necesite $100$ iteraciones pero que solo necesite una unidad de tiempo por iteración. Lo que lleva a buscar un equilibrio entre el coste del cálculo de la función heurística y el número de expansiones que ahorramos al utilizarla. En este sentido, es posible que una función heurística peor acabe dando mejor resultado.
De todo lo anterior deducimos que la heurística controla el comportamiento de $A^*$. Concretamente:
* En un extremo tenemos el caso en el que $h(n)=0$ siempre. Entonces, solo $coste(n)$ jugará algún papel en el algoritmo, y $A^*$ se convierte en el **algoritmo de Dijkstra**, que garantiza encontrar el camino mínimo.
* Si $h(n)\leq h^∗(n)$ entonces se garantiza que $A^*$ encontrará el camino más corto. Cuanto menor sea $h(n)$ más nodos tendrá que expandir $A^*$ y su ejecución será más lenta.
* Si $h(n)=h^∗(n)$, entonces $A^*$ solo seguirá caminos óptimos, y será más rápido (pero puede seguir expandiendo muchos nodos si hay muchos caminos mínimos de igual longitud). Aunque en general será difícil estar en el caso de una $h$ perfecta, es interesante saber que con información perfecta, $A^*$ se comporta perfectamente.
* Si $h(n)$ no es admisible, es decir, a veces es mayor que $h^∗(n)$, entonces $A^*$ no garantiza encontrar el camino mínimo, pero puede encontrar un camino al objetivo muy rápido.
* Por último, si $h(n)$ es muy grande en relación con $coste(n)$, entonces solo $h(n)$ tendrá alguna influencia sobre $A^*$, convirtiendo el algoritmo en un **Algoritmo Voraz**.
En el caso en que haya muchos caminos óptimos (por ejemplo, cuando estamos trabajando con un problema en el que hay muchos estados que tienen un coste similar), $A^*$ tendrá que ir abriendo muchos nodos para encontrar finalmente alguno de esos caminos. Si queremos acelerar la búsqueda en esos casos habrá que modificar la heurística para romper los **empates** (en la literatura esta técnica se llama *tie-breaking*). Por supuesto, en general la forma de hacerlo dependerá del problema concreto, pero también hay aproximaciones generales como, por ejemplo, de todos los nodos que tienen valor actual de $g$ mínimo seleccionar aquellos que tienen $h$ mínimo (seleccionando primero aquellos hijos que están más cerca del objetivo), o aquellos que tienen $coste$ mínimo (los hijos que están más cerca del inicio). Lo importante es dar algún procedimiento por el cual $A^*$ pueda mantener el orden de selección de los hijos, de forma que explote siempre el mismo camino y así no se pierda en abrir muchos caminos que sean similares, por lo que otra opción es usar una lista ordenada donde se van almacenando los nodos más prometedores, y se selecciona siguiendo este orden (algo parecido a lo que se hace en una búsqueda DFS). Cuando se trabaja con búsquedas en terrenos (algo muy común en aplicaciones de $A^*$ a juegos y navegación) se suele usar una heurística que modifica ligeramente las distancias calculadas (con Manhattan, máximo, euclídea, etc.) para romper los empates.
A veces, como en el caso de los juegos, puede ser interesante tener caminos que no sean óptimos, pero sí se obtengan rápidamente y sean suficientemente buenos, por lo que jugar con las ideas anteriores puede dar resultados deseables aunque dejemos de trabajar con heurísticas admisibles. Por ejemplo, cuando usamos $A^*$ para generar soluciones finales a partir de propiedades (es decir, que no conocemos exactamente el estado asociado, sino algunas restricciones que debe cumplir), y no nos interesa tanto el camino como el ser capaces de llegar.
## Búsquedas Estocásticas: Templado Simulado
Cuando los espacios de búsqueda son extremadamente grandes o tienen estructuras relativamente complejas, los procedimientos de búsqueda deterministas suelen obtener muy malos resultados. La **Búsqueda Estocástica** introduce factores de aleatoriedad en esos procesos de forma que, bien usada, puede reducir considerablemente la complejidad del problema. Por supuesto, en este proceso se pierde algo, y es que se sustituye la optimalidad por la tratabilidad en tiempo (es decir, el problema se puede resolver en un tiempo razonable, pero ya no podemos estar seguros de que vayamos a encontrar la solución óptima siempre).
Hay dos algoritmos de búsqueda estocásticos triviales que podemos identificar claramente:
* **Búsqueda Aleatoria**: En cada paso, se selecciona al azar un elemento del espacio de búsqueda y comprobamos si tiene las propiedades deseadas.
* **Camino Aleatorio sin información**: En cada paso, se selecciona al azar un vecino del estado actual y nos desplazamos a él.
Obviamente, estas dos modificaciones para introducir la aleatoriedad tienen pocas opciones de ser eficientes en espacios relativamente grandes, pero suponen un punto de partida sobre el que construir otros algoritmos estocásticos que arrojan buenos resultados. El más famoso de ellos es el algoritmo del **Templado Simulado** (o **Enfriamiento Simulado**).
Hay muchas veces en los que los algoritmos de búsqueda por ascenso se quedan atascados enseguida en óptimos no demasiado buenos. Para estos casos se han diseñado algoritmos que a veces pueden dar soluciones relativamente buenas. El algoritmo del **Templado Simulado** (**Simulated Annealing**) está inspirado en un fenómeno físico que se observa en el templado de metales y en la cristalización de disoluciones:
!!!note: Templado Simulado en el Mundo Físico
Todo conjunto de átomos o moléculas tiene un estado de energía que depende de cierta función de la temperatura del sistema. A medida que lo vamos enfriando, el sistema va perdiendo energía hasta que se estabiliza. El fenómeno físico que se observa es que, dependiendo de cómo se realiza el enfriamiento, el estado de energía final es muy diferente. Por ejemplo, si una barra de metal se enfría demasiado rápido la estructura cristalina a la que se llega al final está poco cohesionada (un número bajo de enlaces entre átomos) y ésta se rompe con facilidad. Si el enfriamiento se realiza más lentamente, el resultado final es totalmente diferente, el número de enlaces entre los átomos es mayor, y se obtiene una barra mucho más difícil de romper. Durante este enfriamiento controlado se observa que la energía del conjunto de átomos no disminuye de manera constante, sino que a veces la energía total puede ser mayor que en un momento inmediatamente anterior. Esta circunstancia hace que el estado de energía final que se alcanza sea mejor que cuando el enfriamiento se hace rápidamente.
A partir de este fenómeno físico se puede obtener un algoritmo que permite, en ciertos problemas, obtener soluciones mejores que las proporcionadas por los algoritmos vistos hasta ahora. En este algoritmo el nodo siguiente a explorar no será siempre el mejor vecino, sino que se elige aleatoriamente (en función de los valores de unos parámetros) de entre todos los vecinos (los buenos y los malos). Una ventaja de este algoritmo es que no hay por qué generar todos los sucesores de un nodo, basta elegir un sucesor al azar y decidir si continuamos por él o no.
El algoritmo de templado simulado intenta transportar la analogía física al problema que se quiere solucionar:
* En primer lugar, se denomina **función de energía** a la función heurística que mide la calidad de una solución.
* Tendremos un parámetro de control que denominaremos **temperatura**, que permitirá controlar el funcionamiento del algoritmo.
* También se tendrá una función que dependerá de la temperatura y de la diferencia de calidad entre el nodo actual y un sucesor. Esta función dirigirá la elección de los sucesores de la forma siguiente:
* Cuanta mayor sea la temperatura, más probabilidad habrá de que al generar como sucesor un estado peor éste sea elegido.
* La elección de un estado peor dependerá de su diferencia de calidad con el estado actual, cuanta más diferencia, menos probabilidad de elegirlo.
* El último elemento es la **estrategia de enfriamiento**. Por ejemplo, el algoritmo podría realizar un número total de iteraciones prefijado y cada cierto número de ellas el valor de la temperatura disminuye en cierta cantidad, partiendo desde una temperatura inicial y llegando a cero (o a un valor mínimo) en la última iteración. La elección de estos dos parámetros (**número total de iteraciones** y **número de iteraciones entre cada bajada de temperatura**) determina el comportamiento completo del algoritmo, y puede modificar su eficiencia de forma dramática. Aunque hay algunos resultados teóricos acerca de la influencia de estos parámetros, en general hay que decidir experimentalmente cuál es la temperatura inicial más adecuada y también la forma más adecuada de hacer que vaya disminuyendo.
~~~~~~~~
Algoritmo: Templado Simulado (T₀, s₀, N, γ < 1, ϵ > 0)
Temp = T₀
while Temp > ϵ
Repeat N:
s₁ = one-of(T(s₀))
∆E = E(s₀) − E(s₁)
if ∆E > 0
s₀ = s₁
else
con probabilidad exp(∆E/Temp): s₀ = s₁
Temp = Temp ⋅ γ
return s₀
~~~~~~~~
Como en la analogía física, si el número de pasos es muy pequeño, la temperatura bajará muy rápidamente, y el camino explorado será relativamente aleatorio. Si el número de pasos es más grande, la bajada de temperatura será más suave y la búsqueda será mejor. El algoritmo favorece la disminución de la energía, $E$, ya que $\Delta E>0$ es equivalente a que $E(s_0)>E(s_1)$, y en ese caso $s_1$ se convierte en el estado actual. Cuando $\Delta E < 0$, se tiene que $e^{\Delta E/Temp} < 1$ y, de hecho:
$$\displaystyle \lim_{Temp\to 0} e^{\Delta E/Temp}=0$$
por lo que el hecho de admitir nuevos estados que empeoran la búsqueda se hace cada vez más improbable a medida que avanza el algoritmo. Además, los estados que empeoran mucho la energía (es decir, aquellos que hacen que $\Delta E$ sea más negativo) se hacen menos probables que los que la empeoran menos.
Es importante observar que la búsqueda se ha transformado en un problema de optimización (en este caso, de minimización), porque realmente pasamos de buscar un estado con ciertas propiedades generales a buscar un estado que tiene valor mínimo respecto a la función de energía considerada. Esta función tiene muchas similitudes con las funciones heurísticas de algoritmos como $A^∗$, ya que de alguna forma mide lo buena, o cerca de la solución ideal, que está el estado actual, pero tiene una ventaja computacional, y es que no imponemos ninguna propiedad adicional (en $A^∗$, la función heurística debía ser admisible para asegurar la convergencia a la solución, por ejemplo). En cualquier caso, a $E$ se le supone un comportamiento bastante básico:
1. $E(s)\geq 0$, para cualquier estado, $s$, de nuestro espacio.
2. $E(s)=0$ solo en el caso en que $s$ sea una solución adecuada del problema.
3. $E(s_1) < E(s_2)$, si $s_1$ es *mejor solución* que $s_2$.
Este algoritmo es especialmente bueno para problemas con un espacio de búsqueda grande en los que el óptimo global está rodeado de muchos óptimos locales, ya que le es más fácil escapar de ellos. Se puede utilizar también para problemas en los que encontrar una heurística discriminante es difícil (una elección aleatoria es tan buena como otra cualquiera), ya que en estos casos el algoritmo de ascenso de colinas no tiene mucha información con la que trabajar y se queda atascado enseguida, mientras que el templado simulado puede explorar más espacio de soluciones y tiene mayor probabilidad de encontrar una solución buena. Además, los requerimientos de la función de energía son bastante menores que los que se le piden a las heurísticas (admisibilidad, por ejemplo), lo que hace que el modelado se simplifique considerablemente.
El mayor problema de este algoritmo es determinar los valores de los parámetros, y requiere una importante labor de experimentación que depende de cada problema. Los valores óptimos de estos parámetros varían con el dominio e incluso con el tamaño de la instancia concreta del problema.