Tema CS1: Introducción a Maxima
(Ejercicios resueltos)

1 Primeros pasos con Maxima

Ejercicio 1.1. Calcular el valor de 5+(2/3)^(-2)

(%i1) 5+(2/3)^(-2);

2 Maxima como calculadora

Ejercicio 2.1. Calcular el factorial de 100.

(%i2) 100!;

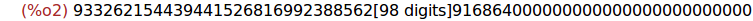
Ejercicio 2.2. Observad que no se han mostrado todas las cifras.
Obtener todas las cifras cambiando la pantalla 2D.

(%i3) set_display(ascii)$ 100!; set_display(xml)$

Ejercicio 2.3. Calcular la raíz cuadrada de 4.

(%i6) sqrt(4);

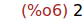
Ejercicio 2.4. Calcular la raíz cuadrada de 5.

(%i7) sqrt(5);

Ejercicio 2.5. Observad que la raiz de 5 la muestra de forma simbólica.
Calcular el valor aproximado del resultado anterior

(%i8) float(%);

Ejercicio 2.6. Asignar a la variable a el valor 5^2.

(%i9) a : 5^2;

Ejercicio 2.7. Calcular el valor de sqrt(a)+1/a

(%i10) sqrt(a)+1/a;

Ejercicio 2.8. Asignar a la variable c el valor b^2.

(%i11) c:b^2;

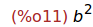
Ejercicio 2.9. Calcular el valor de la raíz cuadrada de c.
Observad que Maxima puede trabajar a nivel simbólico.

(%i12) sqrt(c);

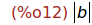
Ejercicio 2.10. Calcular el valor de a+A.
Observad que Maxima distingue entre letras minúsculas y mayúsculas.

(%i13) a+A;

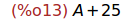
Ejercicio 2.11. Calcular los valores de Exp(0) y de exp(0).

(%i14) Exp(0); exp(0);

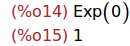
Ejercicio 2.13. Calcular el logaritmo neperiano de e.

(%i16) log(%e);

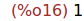
Ejercicio 2.14. Calcular el valor de la constante pi.

(%i17) %pi;

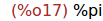
Ejercicio 2.15. Calcular el valor aproximado de pi.

(%i18) float(%pi);

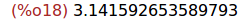
Ejercicio 2.16. Calcular el valor de pi con 100 cifras decimales.

(%i19) fpprec : 100;

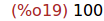
(%i20) bfloat(1000*%pi);

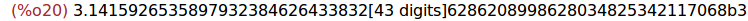
(%i21) set_display(ascii)$ bfloat(1000*%pi); set_display(xml)$

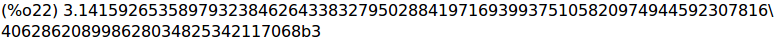
3 Los complejos

Ejercicio 3.1. Calcular la raíz cuadrada de -1.

(%i24) sqrt(-1);

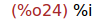
Ejercicio 3.2. Calcular el cuadrado de la unidad imaginaria.

(%i25) %i^2;

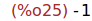
Ejercicio 3.3. Asignar a z el número complejo (1+i)^2/(1-2*i)

(%i26) z : (1+%i)^2/(1-2*%i);

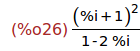
Ejercicio 3.4. Calcular la forma cartesiana de z.

(%i27) rectform(%);

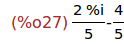
Ejercicio 3.5. Calcular la parte real de z.

(%i28) realpart(z);

Ejercicio 3.6. Calcular la parte imaginaria de z.

(%i29) imagpart(z);

Ejercicio 3.7. Calcular el módulo de z.

(%i30) abs(z) ;

Ejercicio 3.8. Calcular el argumento de z.

(%i31) carg(z);

Ejercicio 3.9. Calcular la forma polar de z.

(%i32) polarform(z);

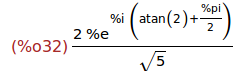
Ejercicio 3.10. Calcular la forma algebraica de z^4

(%i33) rectform(z^4);

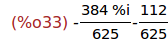
4 Cálculos algebraicos básicos

Ejercicio 4.1. Borrar los valores de todas las variables.

(%i34) remvalue(all)$

Ejercicio 4.2. Asignar a la variable y la expresión (a+b)^4

(%i35) y : (a+b)^4;

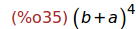
Ejercicio 4.3. Desarrollar la expresión anterior.

(%i36) expand(%);

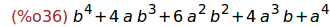
Ejercicio 4.4. Factorizar la expresión anterior.

(%i37) factor(%);

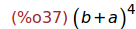
Ejercicio 4.5. Factorizar la expresión (x^4-1)

(%i38) factor(x^4-1);

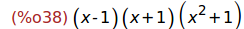
Ejercicio 4.6. Sustituir x por 3/z en la expresión anterior.

(%i39) subst(3/z,x,%);

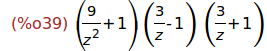
Ejercicio 4.7. Simplificar la expresión anterior.

(%i40) ratsimp(%);

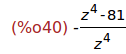
5 Ecuaciones y sistemas de ecuaciones

Ejercicio 5.1. Resolver la ecuación 3*x²-17*x+10=0

(%i41) solve(3*x²-17*x+10=0);

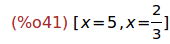
Ejercicio 5.2. Resolver la ecuación x^2+9=0

(%i42) solve(x^2+9=0);

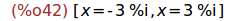
Ejercicio 5.3. Resolver la ecuación 1+z+z^2=0

(%i43) solve(1+z+z^2=0);

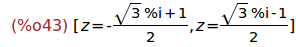
Ejercicio 5.4. Resolver la ecuación a*x^2+b*x+c=0

(%i44) solve(a*x^2+b*x+c=0,x);

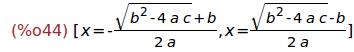
Ejercicio 5.5. Borrar el valor de la variable y.

(%i45) kill(y)$

Ejercicio 5.6. Asignar a la variable sist el sistema de ecuaciones
   m*x+y=1,
   x-m^2*y=m

(%i46) sist : [m*x+y=1, x-m^2*y=m];

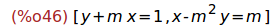
Ejercicio 5.7. Resolver el sistema sist respecto de las variables x e y.

(%i47) solve(sist,[x,y]);

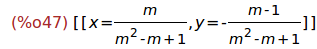
Ejercicio 5.8. Calcular una raiz de la ecuación cos(x)=x entre 0 y pi.

(%i48) find_root(cos(x)=x,x,0,%pi);

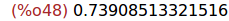
6 Gráficas de funciones

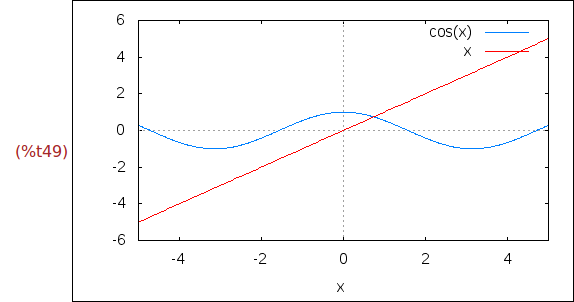
Ejercicio 6.1. Dibujar las gráficas de las funciones
   y=cos(x)
   y=x

(%i49) wxplot2d([cos(x), x], [x,-5,5])$

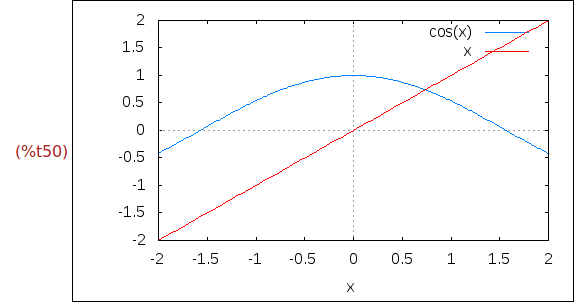
(%i50) wxplot2d([cos(x), x], [x,-2,2])$

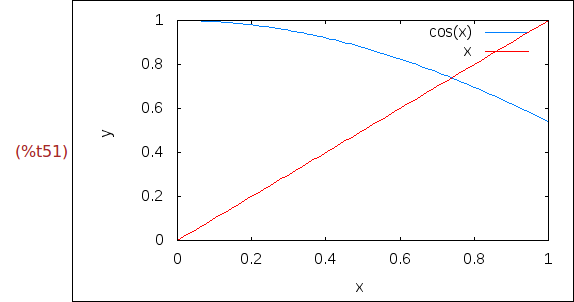
(%i51) wxplot2d([cos(x), x], [x,0,1],[y,0,1])$

7 Obtención de la ayuda para una función

Ejercicio 7.1. Obtener la ayuda de la función 'is'

(%i52) ? is;

Ejercicio 7.2. Comprobar si la raiz cuadrada de t^2 es igual a t.

(%i53) is(sqrt(t^2)=t);

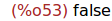
Ejercicio 7.3. Comprobar si la raiz cuadrada de t^2 es igual al valor
absoluto de t.

(%i54) is(sqrt(t^2)=abs(t));

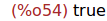
Ejercicio 7.4. Comprobar si t es positivo.

(%i55) is(t>0);

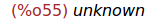
Fin.