Tema 12: Analizadores sintácticos funcionales

Librerías auxiliares

En este tema se usan las siguientes librerías:

import Test.QuickCheck
import Data.Char

1 Analizadores sintácticos

Analizadores sintácticos

Un analizador sintáctico es un programa que analiza textos para determinar su estructura sintáctica.
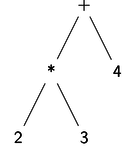
Ejemplo de análisis sintáctico aritmético: La estructura sintáctica de la cadena "2*3+4" es el árbol

El análisis sintáctico forma parte del preprocesamiento en la mayoría de las aplicaciones reales.

2 El tipo de los analizadores sintácticos

Opciones para el tipo de los analizadores sintácticos

Opción inicial:

type Analizador = String -> Tree

Con la parte no analizada:

type Analizador = String -> (Tree,String)

Con todos los análisis:

type Analizador = String -> [(Tree,String)]

Con estructuras arbitrarias:

type Analizador a = String -> [(a,String)]

Simplificación: analizadores que fallan o sólo dan un análisis.

3 Analizadores sintácticos básicos

Analizadores sintácticos básicos: resultado

(analiza a cs) analiza la cadena cs mediante el analizador a. Por ejemplo,

analiza :: Analizador a -> String -> [(a,String)]
analiza a cs = a cs

El analizador resultado v siempre tiene éxito, devuelve v y no consume nada. Por ejemplo,

ghci> analiza (resultado 1) "abc"
[(1,"abc")]

resultado :: a -> Analizador a
resultado v =  \xs -> [(v,xs)]

Analizadores sintácticos básicos: fallo

El analizador fallo siempre falla. Por ejemplo,

ghci> analiza fallo "abc"
[]

fallo :: Analizador a
fallo =  \xs -> []

Analizadores sintácticos básicos: elemento

El analizador elemento falla si la cadena es vacía y consume el primer elemento en caso contrario. Por ejemplo,

ghci> analiza elemento ""
[]
ghci> analiza elemento "abc"
[('a',"bc")]

elemento :: Analizador Char
elemento =  \xs -> case xs of
                     [] -> []
                     (x:xs) -> [(x , xs)]

4 Composición de analizadores sintácticos

4.1 Secuenciación de analizadores sintácticos

((p >*> f) e) falla si el análisis de e por p falla, en caso contrario, se obtiene un valor (v) y una salida (s), se aplica la función f al valor v obteniéndose un nuevo analizador con el que se analiza la salida s.

infixr 5 >*>
(>*>) :: Analizador a -> (a -> Analizador b) -> 
         Analizador b
p >*> f = \ent -> case analiza p ent of
                       []        -> []
                       [(v,sal)] -> analiza (f v) sal

primeroTercero es un analizador que devuelve los caracteres primero y tercero de la cadena. Por ejemplo,

primeroTercero "abel"  ==  [(('a','e'),"l")]
primeroTercero "ab"    ==  []

primeroTercero :: Analizador (Char,Char)
primeroTercero = 
    elemento >*> \x ->
    elemento >*> \_ ->
    elemento >*> \y ->
    resultado (x,y)

4.2 Elección de analizadores sintácticos

((p +++ q) e) analiza e con p y si falla analiza e con q. Por ejemplo,

Main*> analiza (elemento +++ resultado 'd') "abc"  
[('a',"bc")]
Main*> analiza (fallo +++ resultado 'd') "abc"     
[('d',"abc")]
Main*> analiza (fallo +++ fallo) "abc"             
[]

(+++) :: Analizador a -> Analizador a -> Analizador a
p +++ q = \ent -> case analiza p ent of
                    []        -> analiza q ent
                    [(v,sal)] -> [(v,sal)]

5 Primitivas derivadas

(sat p) es el analizador que consume un elemento si dicho elemento cumple la propiedad p y falla en caso contrario. Por ejemplo,

analiza (sat isLower) "hola"  ==  [('h',"ola")]
analiza (sat isLower) "Hola"  ==  []

sat :: (Char -> Bool) -> Analizador Char
sat p = elemento >*> \x ->
        if p x then resultado x else fallo

digito analiza si el primer carácter es un dígito. Por ejemplo,

analiza digito "123"  ==  [('1',"23")]
analiza digito "uno"  ==  []

digito :: Analizador Char
digito = sat isDigit

minuscula analiza si el primer carácter es una letra minúscula. Por ejemplo,

analiza minuscula "eva"  ==  [('e',"va")]
analiza minuscula "Eva"  ==  []

minuscula :: Analizador Char
minuscula = sat isLower

mayuscula analiza si el primer carácter es una letra mayúscula. Por ejemplo,

analiza mayuscula "Eva"  ==  [('E',"va")]
analiza mayuscula "eva"  ==  []

mayuscula :: Analizador Char
mayuscula = sat isUpper

letra analiza si el primer carácter es una letra. Por ejemplo,

analiza letra "Eva"  ==  [('E',"va")]
analiza letra "eva"  ==  [('e',"va")]
analiza letra "123"  ==  []

letra :: Analizador Char
letra = sat isAlpha

alfanumerico analiza si el primer carácter es una letra o un número. Por ejemplo,

analiza alfanumerico "Eva"   ==  [('E',"va")]
analiza alfanumerico "eva"   ==  [('e',"va")]
analiza alfanumerico "123"   ==  [('1',"23")]
analiza alfanumerico " 123"  ==  []

alfanumerico :: Analizador Char
alfanumerico = sat isAlphaNum

(caracter x) analiza si el primer carácter es igual al carácter x. Por ejemplo,

analiza (caracter 'E') "Eva"  ==  [('E',"va")]
analiza (caracter 'E') "eva"  ==  []

caracter :: Char -> Analizador Char
caracter x = sat (== x)

(cadena c) analiza si empieza con la cadena c. Por ejemplo,

analiza (cadena "abc") "abcdef"  ==  [("abc","def")]
analiza (cadena "abc") "abdcef"  ==  []

cadena :: String -> Analizador String
cadena []     = resultado []
cadena (x:xs) = caracter x >*> \x  ->
                cadena xs  >*> \xs ->
                resultado (x:xs)

varios p aplica el analizador p cero o más veces. Por ejemplo,

analiza (varios digito) "235abc"  ==  [("235","abc")]
analiza (varios digito) "abc235"  ==  [("","abc235")]

varios :: Analizador a -> Analizador [a]
varios p  = varios1 p +++ resultado []

varios1 p aplica el analizador p una o más veces. Por ejemplo,

analiza (varios1 digito) "235abc"  ==  [("235","abc")]
analiza (varios1 digito) "abc235"  ==  []

varios1 :: Analizador a -> Analizador [a]
varios1 p = p        >*> \v  ->
            varios p >*> \vs ->
            resultado (v:vs)

ident analiza si comienza con un identificador (i.e. una cadena que comienza con una letra minúscula seguida por caracteres alfanuméricos). Por ejemplo,

ghci> analiza ident "lunes12 de Ene"  
[("lunes12"," de Ene")]
ghci> analiza ident "Lunes12 de Ene"  
[]

ident :: Analizador String
ident =  minuscula           >*> \x  ->
         varios alfanumerico >*> \xs ->
         resultado (x:xs)

nat analiza si comienza con un número natural. Por ejemplo,

analiza nat "14DeAbril"   ==  [(14,"DeAbril")]
analiza nat " 14DeAbril"  ==  []

nat :: Analizador Int
nat = varios1 digito >*> \xs ->
      resultado (read xs)

espacio analiza si comienza con espacios en blanco. Por ejemplo,

analiza espacio "    a b c"  ==  [((),"a b c")]

espacio :: Analizador ()
espacio = varios (sat isSpace) >*> \_ -> 
          resultado ()

6 Tratamiento de los espacios

unidad p ignora los espacios en blanco y aplica el analizador p. Por ejemplo,

ghci> analiza (unidad nat) " 14DeAbril"     
[(14,"DeAbril")]
ghci> analiza (unidad nat) " 14   DeAbril"  
[(14,"DeAbril")]

unidad :: Analizador a -> Analizador a
unidad p = espacio >*> \_ ->
           p       >*> \v ->
           espacio >*> \_ ->
           resultado v

identificador analiza un identificador ignorando los espacios delante y detrás. Por ejemplo,

ghci> analiza identificador "  lunes12  de Ene"
[("lunes12","de Ene")]

identificador :: Analizador String
identificador = unidad ident

natural analiza un número natural ignorando los espacios delante y detrás. Por ejemplo,

analiza natural "  14DeAbril"  ==  [(14,"DeAbril")]

natural :: Analizador Int
natural =  unidad nat

(simbolo xs) analiza la cadena xs ignorando los espacios delante y detrás. Por ejemplo,

ghci> analiza (simbolo "abc") "  abcdef"  
[("abc","def")]

simbolo :: String -> Analizador String
simbolo xs =  unidad (cadena xs)

listaNat analiza una lista de naturales ignorando los espacios. Por ejemplo,

ghci> analiza listaNat " [  2,  3, 5   ]"  
[([2,3,5],"")]
ghci> analiza listaNat " [  2,  3,]"       
[]

listaNat :: Analizador [Int]
listaNat = simbolo "["          >*> \_ ->
           natural              >*> \n ->
           varios (simbolo ","  >*> \_ ->
                   natural)     >*> \ns ->
           simbolo "]"          >*> \_ ->
           resultado (n:ns)

7 Analizador de expresiones aritméticas

Expresiones aritméticas

Consideramos expresiones aritméticas:
- construidas con números, operaciones (+ y *) y paréntesis.
- + y * asocian por la derecha.
- * tiene más prioridad que +.
Ejemplos:
- 2+3+5 representa a 2+(3+5).
- 2*3+5 representa a (2*3)+5.

Gramáticas de las expresiones aritméticas: Gramática 1

Gramática 1 de las expresiones aritméticas:

expr ::=  expr + expr | expr * expr | (expr) | nat 
nat  ::=  0 | 1 | 2 | ...

La gramática 1 no considera prioridad: acepta 2+3*5 como (2+3)*5 y como 2+(3*5)
La gramática 1 no considera asociatividad: acepta 2+3+5 como (2+3)+5 y como 2+(3+5)
La gramática 1 es ambigua.

Gramáticas de las expresiones aritméticas: Gramática 2

Gramática 2 de las expresiones aritméticas (con prioridad):

expr    ::=  expr + expr | term 
term    ::=  term * term | factor 
factor  ::=  (expr) | nat 
nat     ::=  0 | 1 | 2 | dots

La gramática 2 sí considera prioridad: acepta 2+3*5 sólo como 2+(3*5)
La gramática 2 no considera asociatividad: acepta 2+3+5 como (2+3)+5 y como 2+(3+5)
La gramática 2 es ambigua.

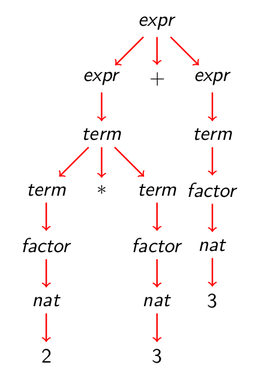
Árbol de análisis sintáctico de 2*3+5 con la gramática 2

Gramáticas de las expresiones aritméticas: Gramática 3

Gramática 3 de las expresiones aritméticas:

expr   ::= term + expr | term 
term   ::= factor * term | factor 
factor ::= (expr) | nat 
nat    ::= 0 | 1 | 2 | dots

La gramática 3 sí considera prioridad: acepta 2+3*5 sólo como 2+(3*5)
La gramática 3 sí considera asociatividad: acepta 2+3+5 como 2+(3+5)
La gramática 3 no es ambigua (i.e. es libre de contexto).

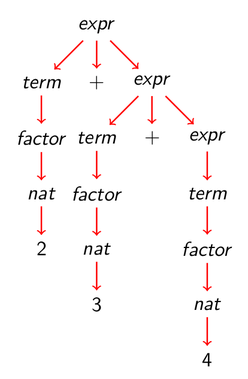
Árbol de análisis sintáctico de 2+3+5 con la gramática 3

Gramáticas de las expresiones aritméticas: Gramática 4

La gramática 4 se obtiene simplificando la gramática 3:

expr   ::= term (+ expr | epsilon) 
term   ::= factor (* term | epsilon) 
factor ::= (expr) | nat 
nat    ::= 0 | 1 | 2 | dots

donde ε es la cadena vacía.

La gramática 4 no es ambigua.
La gramática 4 es la que se usará para escribir el analizador de expresiones aritméticas.

Analizador de expresiones aritméticas

expr analiza una expresión aritmética devolviendo su valor. Por ejemplo,

analiza expr "2*3+5"     ==  [(11,"")]
analiza expr "2*(3+5)"   ==  [(16,"")]
analiza expr "2+3*5"     ==  [(17,"")]
analiza expr "2*3+5abc"  ==  [(11,"abc")]

expr :: Analizador Int
expr = term              >*> \t ->
       (simbolo "+"      >*> \_ ->              
        expr             >*> \e ->
        resultado (t+e))
       +++ resultado t

term analiza un término de una expresión aritmética devolviendo su valor. Por ejemplo,

analiza term "2*3+5"      ==  [(6,"+5")]
analiza term "2+3*5"      ==  [(2,"+3*5")]
analiza term "(2+3)*5+7"  ==  [(25,"+7")]

term :: Analizador Int
term =  factor            >*> \f ->
        (simbolo "*"      >*> \_ ->
         term             >*> \t ->
         resultado (f*t))
        +++ resultado f

factor analiza un factor de una expresión aritmética devolviendo su valor. Por ejemplo,

analiza factor "2*3+5"      ==  [(2,"*3+5")]
analiza factor "(2+3)*5"    ==  [(5,"*5")]
analiza factor "(2+3*7)*5"  ==  [(23,"*5")]

factor :: Analizador Int
factor =  (simbolo "("  >*> \_ ->
           expr         >*> \e ->
           simbolo ")"  >*> \_ ->
           resultado e)
          +++ natural

(valor cs) analiza la cadena cs devolviendo su valor si es una expresión aritmética y un mensaje de error en caso contrario. Por ejemplo,

valor "2*3+5"      ==  11
valor "2*(3+5)"    ==  16
valor "2 * 3 + 5"  ==  11
valor "2*3x"       ==  *** Exception: sin usar x
valor "-1"         ==  *** Exception: entrada no valida

valor :: String -> Int
valor xs = case (analiza expr xs) of
             [(n,[])]  -> n
             [(_,sal)] -> error ("sin usar " ++ sal)
             []        -> error "entrada no valida"

8 Bibliografía

R. Bird. Introducción a la programación funcional con Haskell. Prentice Hall, 2000.
- Cap. 11: Análisis sintáctico.
G. Hutton. Programming in Haskell. Cambridge University Press, 2007.
- Cap. 8: Functional parsers.
G. Hutton y E. Meijer. Monadic parser combinators. Technical Report NOTTCS-TR-96-4, Department of Computer Science, University of Nottingham, 1996.
G. Hutton y E. Meijer. Monadic parsing in Haskell. Journal of Functional Programming, 8(4): 437-444, 1998.
B.C. Ruiz, F. Gutiérrez, P. Guerrero y J.E. Gallardo. Razonando con Haskell. Thompson, 2004.
- Cap. 14: Analizadores.

José A. Alonso Jiménez
Grupo de Lógica Computacional
Dpto. de Ciencias de la Computación e I.A.
Universidad de Sevilla