limsup |f(x)/g(x)| < ∞
x → ∞Intuitivamente, sólo se considera el término más importante y se ignoran los factores constantes.
Si g ∈ O(f) y h ∈ O(f), entonces g+h ∈ O(f)
Si f ∈ O(g) y g ∈ O(h), entonces f ∈ O(h)
f+g ∈ O(max(f,g))
O(f+g) = O(max(f,g))
Si f ∈ O(f') y g ∈ O(g'), entonces f+g ∈ O(f'+g')
Si f ∈ O(f') y g ∈ O(g'), entonces f.g ∈ O(f'.g')
Si f ∈ O(g) y a ∈ ℜ⁺-{0}, entonces a.f ∈ O(g)
Si f ∈ O(g) y n ≥ 1, entonces fⁿ ∈ O(gⁿ)
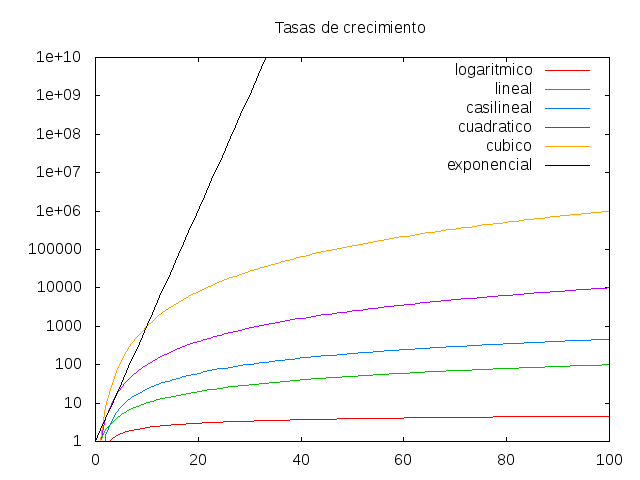
Orden Nombre O(1) constante O(log n) logarítmica O(n) lineal O(n log n) casi lineal O(n²) cuadrática O(n³) cúbica O(a^n) exponencial
T(n) n = 100 n = 200 log(n) 1 h. 1.15 h. n 1 h. 2 h. nlog(n) 1 h. 2.30 h. n² 1 h. 4 h. n³ 1 h. 8 h. 2ⁿ 1 h. 1.27*10³⁰ h.
T(n) t = 1h t = 2h log(n) n = 100 n = 10000 n n = 100 n = 200 nlog(n) n = 100 n = 178 n² n = 100 n = 141 n³ n = 100 n = 126 2ⁿ n = 100 n = 101
suma 5 == 15suma :: Integer -> Integer
suma 0 = 0
suma n = n + suma (n-1)
n segs 1000 0.02 2000 0.03 3000 0.04 4000 0.04 5000 0.05 6000 0.06 7000 0.07 8000 0.08
tiempo(suma n) ≈ n * 0.00001El tiempo necesario para calcular (suma n) es proporcional al número T(n) de operaciones elementales necesarias para evaluar la expresión.
Las ecuaciones para calcular T(n) son
T(1) = 1
T(n+1) = 1 + T(n)T(1) = 1 [por definición de T]
T(n+1) = 1+T(n) [por definición de T]
= 1+n [por hipótesis de inducción]
= n+1 [por álgebra]suma2 :: Integer -> Integer
suma2 n = n*(n+1) `div` 2
n segs. 1000 0.01 2000 0.01 3000 0.01 4000 0.01 5000 0.01 6000 0.01 7000 0.01 8000 0.01
tiempo(suma n) ≈ 0.01T(1) = 1sumaDeSumas n = (suma 0) + (suma 1) + ... + (suma n)sumaDeSumas :: Integer -> Integer
sumaDeSumas 0 = 0
sumaDeSumas n = suma n + sumaDeSumas (n-1)
n segs 100 0.06 200 0.17 300 0.35 400 0.62 500 0.96 600 1.37
T(1) = 1
T(n+1) = T(suma(n+1))+T(n)
= n+1+T(n)T(1) = 1 ≤ 1²T(n+1)
= n+1+T(n) [por coste de sumaDeSumas.2]
≤ n+1+n² [por hip. de inducción]
≤ n²+2n+1 [por álgebra]
= (n+1)² [por álgebra]x(0) = 1
x(n+1) = (x/x(n) + x(n))/2Por ejemplo,
ghci> raiz 9 5
3.0
ghci> raiz 16 5
4.0000005
ghci> raiz 16 10
4.0raiz :: Float -> Int -> Float
raiz x 0 = 1
raiz x n = (x / (raiz x (n-1)) + (raiz x (n-1))) / 2.0
n segs 14 0.14 15 0.27 16 0.53 17 1.04 18 2.03 19 4.08 20 8.10
T(0) = 1
T(n+1) = 2*T(n)T(0) = 1 = 2^0T(n+1)
= 2*T(n) [por coste de raiz]
= 2*2ⁿ [por hip. de inducción]
= 2^(n+1) [por álgebra]x^n = (x*x)^(n/2), si n es par
x^n = x*(x*x)^(n/2), si n es imparpotencia :: Integer -> Integer -> Integer
potencia x 0 = 1
potencia x n | even n = potencia (x*x) (div n 2)
| otherwise = x * potencia (x*x) (div n 2)
n segs 1024 0.01 2048 0.02 4096 0.04 8192 0.07 16384 0.14 32768 0.26
T(1) = 1
T(n) = 1 + T(n/2)T(1) = 1 = 1 + log 1T(n)
= 1 + T(n/2) [por coste de potencia]
= 1 + (1 + log(n/2)) [por hipótesis de inducción]
= 1 + (1 + log n - 1) [por álgebra]
= 1 + log n [por álgebra]inversa [3,2,5,7] == [7,5,2,3]inversa1 [] = []
inversa1 (x:xs) = inversa1 xs ++ [x]T(0) = 1
T(n+1) = T(n) + n + 1Por tanto, inversa1 ∈ O(n²)
Nota: Las ecuaciones de coste se pueden resolver con Wolfram Alpha.
inversa2 :: [a] -> [a]
inversa2 xs = aux [] xs
where aux ys [] = ys
aux ys (x:xs) = aux (x:ys) xsT(0) = 1
T(n+1) = 1 + T(n) Por tanto, inversa1 ∈ O(n)
Nota: Las ecuaciones de coste se pueden resolver con Wolfram Alpha.
| Ecuaciones | Orden | Ejemplo |
|--------------------|------------|-------------|
| T(1) = k | O(1) | suma2 |
|--------------------|------------|-------------|
| T(1) = k | O(n) | suma |
| T(n+1) = T(n)+k' | | |
|--------------------|------------|-------------|
| T(1) = k | O(n²) | sumaDeSumas |
| T(n+1) = T(n)+n | | |
|--------------------|------------|-------------|
| T(1) = k | O(log(n)) | potencia |
| T(n) = T(n/2)+k' | | |
|--------------------|------------|-------------|
| T(0) = k | O(2ⁿ) | raiz |
| T(n+1) = 2T(n)+k' | | |
|--------------------|------------|-------------|
| T(1) = k | O(nlog(n)) | ordenación |
| T(n) = 2T(n/2)+n | | por mezcla |J.L. Balcázar Apuntes sobre el cálculo de la eficiencia de los algoritmos.
R. Pattis Complexity of Python operations