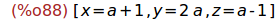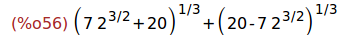
Tema CS1: Introducción a Maxima
(Soluciones de ejercicios propuestos)

En esta relación se presenta ejercicios del tema CS1. En la relación se
usarán las siguientes funciones: abs, bfloat, carg, expand, factor,
find_root, float, fpprec, is, linsolve, plot2D, radcan, rectform y solve.

1 Ejercicio 1

Ejercicio 1.1. Definir la constante a igual a
   (20+14*sqrt(2))^(1/3) + (20-14*sqrt(2))^(1/3)

(%i56) a : (20+14*sqrt(2))^(1/3) + (20-14*sqrt(2))^(1/3);

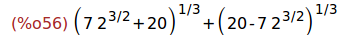
Ejercicio 1.2. Calcular el valor numérico de a. ¿A qué entero se aproxima?
Nota: Usar la función round.

(%i57) round(float(a));

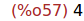
Ejercicio 1.3. Confirmar la conjetura con la orden is(...)

(%i58) is(abs(a-4)<10^-9);

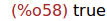
(%i59) is(a=4);

2 Ejercicio 2

Ejercicio 2.1. Escribir el número
   (sin(%pi/3)+cos(%pi/3))^9
en la forma a+b*c^d, donde a, b, c y d son números racionales.

Nota: Cambiar el valor de la variable %piargs a true y usar radcan para la
simplificación de radicales.

(%i60) %piargs : true$
radcan((sin(%pi/3)+cos(%pi/3))^9);
%piargs : false$

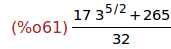
Ejercicio 2.2. Asignar a las variables a, b, c y d los valores obtenidos
en el apartado anterior y calcular el valor de
   (sin(%pi/3)+cos(%pi/3))^9 - a+b*c^d

(%i63) %piargs : true$
a:265/32$
b:17/32$
c:3$
d:5/2$
radcan(radcan((sin(%pi/3)+cos(%pi/3))^9)-(a+b*c^d));
%piargs : false$

3 Ejercicio 3

Ejercicio 3. Calcular la cifra 149 del número pi.

(%i70) fpprec : 150;

(%i71) bfloat(%pi);

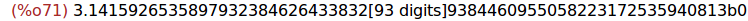
Por tanto, la cifra 149 de pi es 3.

4 Ejercicio 4

Ejercicio 4.1. Asignarle a p el polinomio x^4-x^3-7*x^2-8*x-6

(%i72) p : x^4-x^3-7*x^2-8*x-6;

Ejercicio 4.2. Calcular las raices reales de p.

(%i73) solve(p);

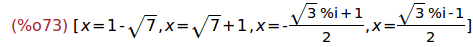
Por tanto, las raices reales de p son 1+sqrt(7) y 1-sqrt(7).

Ejercicio 4.3. Factorizar al máximo el polinomio p.

(%i74) (x-sqrt(7)-1)*(x+sqrt(7)-1)*(x-(sqrt(3)*%i-1)/2)*(x+(sqrt(3)*%i+1)/2);

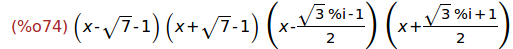
(%i75) ratsimp(%);

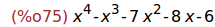
5 Ejercicio 5

Ejercicio 5.1. Asignar a z el número complejo
   ((1-%i*sqrt(3))/(1+%i))^20

(%i76) z : ((1-%i*sqrt(3))/(1+%i))^20;

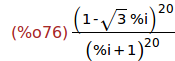
Ejercicio 5.1. Calcular la parte real y la parte imaginaria de z.
Nota: Usar radcan para simplificarla.

(%i77) realpart(z);

(%i78) imagpart(z);

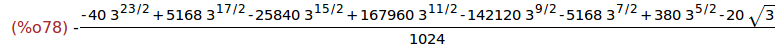
(%i79) radcan(imagpart(z));

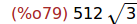
Ejercicio 5.2. Calcular el módulo y el argumento de z.

(%i80) radcan(abs(z));

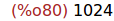
(%i81) radcan(carg(z));

6 Ejercicio 6

Ejercicio 6.1. Con la ayuda de la representación gráfica, conjeturar el
número de soluciones de sin(x)=1-x^4.

(%i82) wxplot2d([sin(x),1-x^4], [x,-2,2],[y,-2,2])$

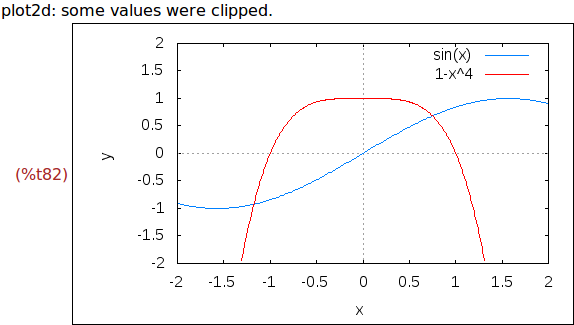
Tiene dos raíces: una entre -1.5 y -1 y la otra entre 0.5 y 1.

Ejercicio 6.2. Dar una aproximación de cada solución.

(%i83) find_root(sin(x)=1-x^4, x, -1.5, -1);

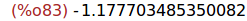
(%i84) find_root(sin(x)=1-x^4, x, 0.5, 1);

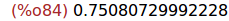
7 Ejercicio 7

Ejercicio 7.1. Borrar el valor de todas las variables.

(%i85) remvalue(all)$

Ejercicio 7.1. Resolver el sistema lineal
   x +2*y=1,
   2*x+4*y=2
Nota: Usar el menú "Ecuaciones / Resolver sistema lineal".

(%i86) linsolve([x+2*y=1, 2*x+4*y=2], [x,y]);

Ejercicio 7.2. Resolver el sistema lineal
   x +2*y=1,
   2*x+4*y=7

(%i87) linsolve([x+2*y=1, 2*x+4*y=7], [x,y]);

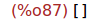
Ejercicio 7.3. Resolver el sistema lineal
   x+z=y,
   2*a*x-y=2*a^2,
   y-2*z=2
en función del parámetro a.

(%i88) linsolve([x+z=y, 2*a*x-y=2*a^2, y-2*z=2],[x,y,z]);