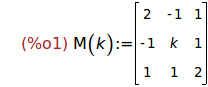
Tema CS6: Matrices en Maxima
(Soluciones de ejercicios propuestos)

1 Ejercicio 1

Ejercicio 1.1. Definir la matriz M(k)
   [ 2 -1 1]
   [-1 k 1]
   [ 1 1 2]
para k en R.

(%i1) M(k) := matrix([2,-1,1],[-1,k,1],[1,1,2]);

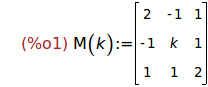
Ejercicio 1.2. Calcular el determinante de M(k).

(%i2) determinant(M(k));

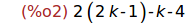
(%i3) expand(%);

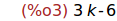
Ejercicio 1.3. Determinar los valores de k para los que M(k) es invertible.

(%i4) solve(%,k);

Por tanto, M(k) es inversible para k distinto de 2.

Ejercicio 1.4. Calcular la inversa de M(k).

(%i5) invert(M(k));

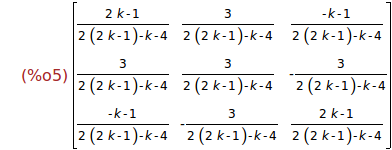
(%i6) ratsimp(%);

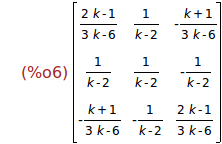
Ejercicio 1.5. Calcular los autovalores de M(k).

(%i7) eigenvalues(M(k));

Ejercicio 1.6. Determinar los k para los que M(k) tiene autovalores múltiples.

(%i8) [x,y,z] : %[1];

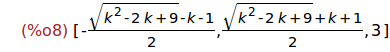
(%i9) realroots(x=y);

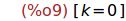
(%i10) solve(x=z);

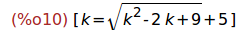
(%i11) wxplot2d([x-z], [k,-50,50])$

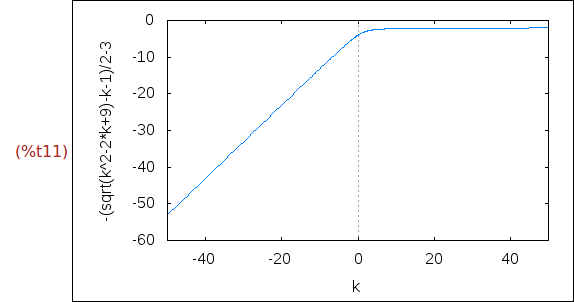
(%i12) solve(y=z);

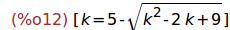
(%i13) wxplot2d([y-z], [k,-50,50])$

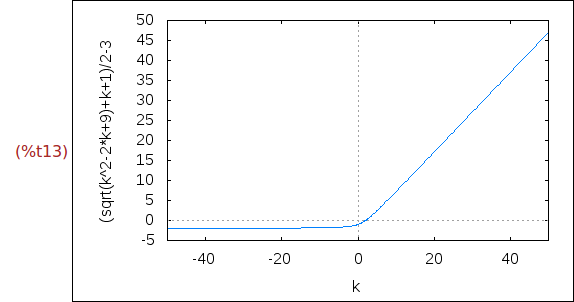
Por tanto, sólo para k=0 tiene autovalores múltiples.

2 Ejercicio 2

Ejercicio 2.1. Definir las matrices A(k) (para k en N) tales que A(k) es la
matriz triangular superior de orden n+1 cuyo término general es
   a(i,j) = binomial(j-1,i-1), si i <= j
          = 0, si i > j

(%i14) a[i,j] := if i <= j then binomial(j-1,i-1) else 0$
A(n) := genmatrix(a,n+1,n+1);

Ejercicio 2.2. Calcular las matrices A(1), A(2) y A(5).

(%i16) A(1);

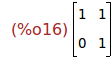
(%i17) A(2);

(%i18) A(5);

Ejercicio 2.3. Calcular las inversas de las matrices A(1), A(2) y A(5).

(%i19) invert(A(1));

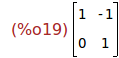
(%i20) invert(A(2));

(%i21) invert(A(5));

Ejercicio 2.4. Conjeturar cuál es la inversa de A(n) y definirla como B(n).

(%i22) b[i,j] := (-1)^(i+j)*a[i,j]$
B(n) := genmatrix(b,n+1,n+1)$
B(5);

Ejercicio 2.5. Comprobar la conjetura para n entre 1 y 10.

(%i25) apply ("and", makelist(is(invert(A(n))=B(n)),n,1,10));

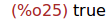
3 Ejercicio 3

El objetivo de este ejercicio ed determinar las matrices cuadradas X de orden 2
que conmutan con la matriz A definida por
   [ 1 -5]
   [-5 3]

Ejercicio 3.1. Escribir la matriz A definida por
   [ 1 -5]
   [-5 3]

(%i26) A : matrix([1,-5],[-5,3]);

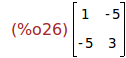
Ejercicio 3.2. Definir la matriz X cuyos términos son a,b,c,d.

(%i27) kill(a,b,c,d)$
X : matrix([a,b],[c,d]);

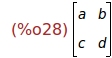
Ejercicio 3.3. Calcular M = AX − XA

(%i29) M : A.X-X.A;

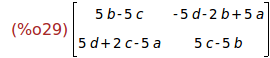
Ejercicio 3.4. Resolver el sistema lineal de 4 ecuaciones con 4 incógnitas M=0.
Indicación: Antes de resolverlo, asignarle a la variable globalsolve el valor
true.

(%i30) globalsolve : true$
solve([M[1,1],M[1,2],M[2,1],M[2,2]]);

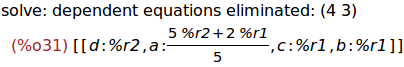
Ejercicio 3.5. Definir las matrices B que son soluciones de la ecuación M=0

(%i32) B : matrix([(5*v+2*u)/5,u],[u,v]);

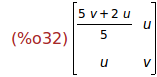
Ejercicio 3.6. Comprobar que A y B conmutan.

(%i33) is(A.B=B.A);