Tema 3: Casos de estudio de programación con Prolog

1 Acumuladores

inversa(+L1,-L2), reverse(L1,L2), se verifica si L2 es la lista inversa de L1. Por ejemplo,

?- inversa([a,b,c],L).
L = [c, b, a]

Definición de inversa con append (no recursiva final):

inversa_1([],[]).
inversa_1([X|L1],L2) :-
   inversa_1(L1,L3),
   append(L3,[X],L2).

Definición de inversa con acumuladores (recursiva final):

inversa_2(L1,L2) :-
   inversa_2_aux(L1,[],L2).

inversa_2_aux([],L,L).
inversa_2_aux([X|L],Acum,L2) :-
   inversa_2_aux(L,[X|Acum],L2).

Comparación de eficiencia

?- findall(_N,between(1,1000,_N),_L1),
   time(inversa_1(_L1,_)), time(inversa_2(_L1,_)).
501,501 inferences in 0.40 seconds
  1,002 inferences in 0.00 seconds

?- findall(_N,between(1,2000,_N),_L1),
   time(inversa_1(_L1,_)), time(inversa_2(_L1,_)).
2,003,001 inferences in 1.59 seconds
    2,002 inferences in 0.00 seconds

?- findall(_N,between(1,4000,_N),_L1),
   time(inversa_1(_L1,_)), time(inversa_2(_L1,_)).
8,006,001 inferences in 8.07 seconds
    4,002 inferences in 0.02 seconds

2 Combinatoria

Combinaciones

combinacion(+L1,+N,-L2) se verifica si L2 es una combinación N-aria de L1. Por ejemplo,

?- combinacion([a,b,c],2,L).
L = [a, b] ;   L = [a, c] ;   L = [b, c] ;  No

combinacion_1(L1,N,L2) :-
   subconjunto(L2,L1),
   length(L2,N).

combinacion_2(L1,N,L2) :-
   length(L2,N),
   subconjunto(L2,L1).

combinacion(L1,N,L2) :-  
   combinacion_2(L1,N,L2).

combinaciones(+L1,+N,-L2) se verifica si L2 es la lista de las combinaciones N-arias de L1. Por ejemplo,

?- combinaciones([a,b,c],2,L).
L = [[a, b], [a, c], [b, c]]

combinaciones_1(L1,N,L2) :-
   findall(L,combinacion_1(L1,N,L),L2).

combinaciones_2(L1,N,L2) :-
   findall(L,combinacion_2(L1,N,L),L2).

combinaciones(L1,N,L2) :-
   combinaciones_2(L1,N,L2).

Comparación de eficiencia de combinaciones

?- findall(_N,between(1,6,_N),_L1), 
   time(combinaciones_1(_L1,2,_L2)),
   time(combinaciones_2(_L1,2,_L2)).
429 inferences in 0.00 seconds
 92 inferences in 0.00 seconds
?- findall(_N,between(1,12,_N),_L1),
   time(combinaciones_1(_L1,2,_L2)),
   time(combinaciones_2(_L1,2,_L2)).
28,551 inferences in 0.01 seconds
   457 inferences in 0.00 seconds
?- findall(_N,between(1,24,_N),_L1),
   time(combinaciones_1(_L1,2,_L2)),
   time(combinaciones_2(_L1,2,_L2)).
117,439,971 inferences in 57.59 seconds
      2,915 inferences in  0.00 seconds

Permutaciones

select(?X,?L1,?L2) se verifica si X es un elemento de la lista L1 y L2 es la lista de los restantes elementos. Por ejemplo,

?- select(X,[a,b,c],L).
X = a   L = [b, c] ;
X = b   L = [a, c] ;
X = c   L = [a, b] ;
No

?- select(a,L,[b,c]).
L = [a, b, c] ;
L = [b, a, c] ;
L = [b, c, a] ;
No

permutacion(+L1,-L2) se verifica si L2 es una permutación de L1. Por ejemplo,

?- permutacion([a,b,c],L).
L = [a, b, c] ;  L = [a, c, b] ;
L = [b, a, c] ;  L = [b, c, a] ;
L = [c, a, b] ;  L = [c, b, a] ;
No

permutacion([],[]).
permutacion(L1,[X|L2]) :-
   select(X,L1,L3),
   permutacion(L3,L2).

Predefinida permutation.

Variaciones

variacion(+L1,+N,-L2) se verifica si L2 es una variación N-aria de L1. Por ejemplo,

?- variacion([a,b,c],2,L).
L=[a,b];L=[a,c];L=[b,a];L=[b,c];L=[c,a];L=[c,b];No

variacion_1(L1,N,L2) :-
   combinacion(L1,N,L3), permutacion(L3,L2).

variacion_2(_,0,[]).
variacion_2(L1,N,[X|L2]) :-
   N > 0, M is N-1,
   select(X,L1,L3),
   variacion_2(L3,M,L2).

variacion(L1,N,L2) :- variacion_2(L1,N,L2).

variaciones(+L1,+N,-L2) se verifica si L2 es la lista de las variaciones N-arias de L1. Por ejemplo,

?- variaciones([a,b,c],2,L).
L = [[a,b],[a,c],[b,a],[b,c],[c,a],[c,b]]

variaciones_1(L1,N,L2) :-
   setof(L,variacion_1(L1,N,L),L2).

variaciones_2(L1,N,L2) :-
   setof(L,variacion_2(L1,N,L),L2).

variaciones(L1,N,L2) :-
   variaciones_2(L1,N,L2).

Comparación de eficiencia de variaciones

?- findall(N,between(1,100,N),L1),
   time(variaciones_1(L1,2,L2)),
   time(variaciones_2(L1,2,L2)).
221,320 inferences in 0.27 seconds
 40,119 inferences in 0.11 seconds
?- findall(N,between(1,200,N),L1),
   time(variaciones_1(L1,2,L2)),
   time(variaciones_2(L1,2,L2)).
1,552,620 inferences in 2.62 seconds
  160,219 inferences in 0.67 seconds
?- findall(N,between(1,400,N),L1),
   time(variaciones_1(L1,2,L2)),
   time(variaciones_2(L1,2,L2)).
11,545,220 inferences in 19.02 seconds
   640,419 inferences in  2.51 seconds

3 Generación y prueba

3.1 Ordenación

Ordenación por generación y prueba

ordenacion(+L1,-L2) se verifica si L2 es la lista obtenida ordenando la lista L1 en orden creciente. Por ejemplo,

?- ordenacion([2,1,a,2,b,3],L). 
L = [a,b,1,2,2,3]

ordenacion(L,L1) :- 
   permutacion(L,L1), 
   ordenada(L1).

ordenada([]).
ordenada([_]).
ordenada([X,Y|L]) :-
   X @=< Y,
   ordenada([Y|L]).

Ordenación por selección

ordenacion_por_seleccion(L1,[X|L2]) :-
   selecciona_menor(X,L1,L3),
   ordenacion_por_seleccion(L3,L2).
ordenacion_por_seleccion([],[]).

selecciona_menor(X,L1,L2) :-
   select(X,L1,L2),
   not((member(Y,L2), Y @< X)).

Ordenación por divide y vencerás

ordenacion_rapida([],[]).
ordenacion_rapida([X|R],Ordenada) :-
   divide(X,R,Menores,Mayores),
   ordenacion_rapida(Menores,Menores_ord),
   ordenacion_rapida(Mayores,Mayores_ord),
   append(Menores_ord,[X|Mayores_ord],Ordenada).

divide(_,[],[],[]).
divide(X,[Y|R],[Y|Menores],Mayores) :-
   Y @< X, !, 
   divide(X,R,Menores,Mayores).
divide(X,[Y|R],Menores,[Y|Mayores]) :-
   \% Y @>= X, 
   divide(X,R,Menores,Mayores).

Ordenación: comparación de eficiencia

Comparación de la ordenación de la lista [N,N-1,N-2,...,2,1]

  |   N | `ordena`           | `selección`            | `rápida`           |
  |-----+--------------------+------------------------+--------------------+
  |   1 |       5 inf 0.00 s |          8 inf  0.00 s |       5 inf 0.00 s |
  |   2 |      10 inf 0.00 s |         19 inf  0.00 s |      12 inf 0.00 s |
  |   4 |      80 inf 0.00 s |         67 inf  0.00 s |      35 inf 0.00 s |
  |   8 | 507,674 inf 0.33 s |        323 inf  0.00 s |     117 inf 0.00 s |
  |  16 |                    |      1,923 inf  0.00 s |     425 inf 0.00 s |
  |  32 |                    |     13,059 inf  0.01 s |   1,617 inf 0.00 s |
  |  64 |                    |     95,747 inf  0.05 s |   6,305 inf 0.00 s |
  | 128 |                    |    732,163 inf  0.40 s |  24,897 inf 0.01 s |
  | 256 |                    |  5,724,163 inf  2.95 s |  98,945 inf 0.05 s |
  | 512 |                    | 45,264,899 inf 22.80 s | 394,497 inf 0.49 s |

3.2 Cuadrado mágico

Cuadrado mágico por generación y prueba

Enunciado: Colocar los números 1,2,3,4,5,6,7,8,9 en un cuadrado 3x3 de forma que todas las líneas (filas, columnas y diagonales) sumen igual.

A B C D E F G H I

cuadrado_1([A,B,C,D,E,F,G,H,I]) :-
   permutacion([1,2,3,4,5,6,7,8,9],
               [A,B,C,D,E,F,G,H,I]),
   A+B+C =:= 15,  D+E+F =:= 15,
   G+H+I =:= 15,  A+D+G =:= 15,
   B+E+H =:= 15,  C+F+I =:= 15,
   A+E+I =:= 15,  C+E+G =:= 15.

Cálculo de soluciones:

?- cuadrado_1(L).
L = [6, 1, 8, 7, 5, 3, 2, 9, 4] ;
L = [8, 1, 6, 3, 5, 7, 4, 9, 2] 
Yes

?- findall(_X,cuadrado_1(_X),_L),length(_L,N).
N = 8 
Yes

Cuadrado mágico por comprobaciones parciales

Programa 2:

cuadrado_2([A,B,C,D,E,F,G,H,I]) :-
   select(A,[1,2,3,4,5,6,7,8,9],L1),
   select(B,L1,L2),
   select(C,L2,L3),  A+B+C =:= 15,
   select(D,L3,L4),
   select(G,L4,L5),  A+D+G =:= 15,
   select(E,L5,L6),  C+E+G =:= 15,
   select(I,L6,L7),  A+E+I =:= 15,
   select(F,L7,[H]), C+F+I =:= 15, D+E+F =:= 15.

Cálculo de soluciones:

?- cuadrado_2(L).
L = [2, 7, 6, 9, 5, 1, 4, 3, 8] ;
L = [2, 9, 4, 7, 5, 3, 6, 1, 8] 
Yes

Comprobación que las dos definiciones dan las mismas soluciones.

?- setof(_X,cuadrado_1(_X),_L),
   setof(_X,cuadrado_2(_X),_L).
Yes

Comparación de eficiencia del cuadrado mágico

?- time(cuadrado_1(_X)).
161,691 inferences in 0.58 seconds

?- time(cuadrado_2(_X)).
  1,097 inferences in 0.01 seconds

?- time(setof(_X,cuadrado_1(_X),_L)).
812,417 inferences in 2.90 seconds

?- time(setof(_X,cuadrado_2(_X),_L)).
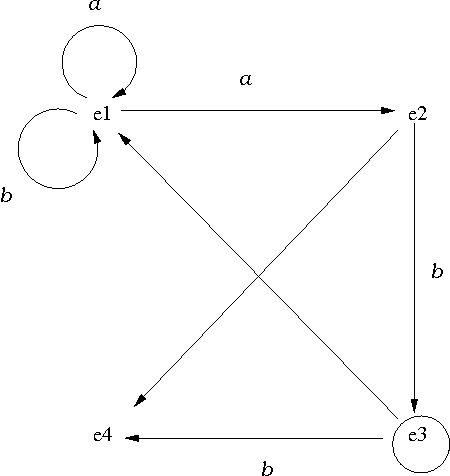
  7,169 inferences in 0.02 seconds

4 Autómatas no deterministas

4.1 Representación de un autómata no determinista

Ejemplo de autómata no determinista (con estado final e3)

Representación de un autómata (automata.pl)

final(E) se verifica si E es el estado final.

final(e3).

trans(E1,X,E2) se verifica si se puede pasar del estado E1 al estado E2 usando la letra X.

trans(e1,a,e1).   trans(e1,a,e2).   trans(e1,b,e1).   
trans(e2,b,e3).
trans(e3,b,e4).

nulo(E1,E2)se verifica si se puede pasar del estado E1 al estado E2 mediante un movimiento nulo.

nulo(e2,e4).
nulo(e3,e1).

4.2 Simulación de los autómatas no deterministas

Simulación de los autómatas no deterministas

acepta(E,L) se verifica si el autómata, a partir del estado E acepta la lista L. Por ejemplo,

acepta(e1,[a,a,a,b]) => Sí
acepta(e2,[a,a,a,b]) => No

acepta(E,[]) :-
   final(E).
acepta(E,[X|L]) :-
   trans(E,X,E1),
   acepta(E1,L).
acepta(E,L) :-
   nulo(E,E1),
   acepta(E1,L).

4.3 Consultas al autómata

Consultas al autómata

Determinar si el autómata acepta la lista [a,a,a,b]

?- acepta(e1,[a,a,a,b]).
Yes

Determinar los estados a partir de los cuales el autómata acepta la lista [a,b]

?- acepta(E,[a,b]).
E=e1 ;
E=e3 ;
No

Determinar las palabras de longitud 3 aceptadas por el autómata a partir del estado e1

?- acepta(e1,[X,Y,Z]).
X = a   Y = a   Z = b ;
X = b   Y = a   Z = b ;
No

5 Problemas de grafos

5.1 Representación de grafos

Grafo de Andalucía

Representación del grafo

arcos(+L) se verifica si L es la lista de arcos del grafo.

arcos([huelva-sevilla,  huelva-cadiz,   
       cadiz-sevilla,   sevilla-malaga, 
       sevilla-cordoba, cordoba-malaga, 
       cordoba-granada, cordoba-jaen,
       jaen-granada,    jaén-almeria,   
       granada-almeria]).

Adyacencia y nodos

adyacente(?X,?Y) se verifica si X e Y son adyacentes.

adyacente(X,Y) :-
   arcos(L),
   (member(X-Y,L) ; member(Y-X,L)).

nodos(?L) se verifica si L es la lista de nodos.

nodos(L) :-
   setof(X,Y^adyacente(X,Y),L).

5.2 Caminos en un grafo

Caminos

camino(+A,+Z,-C) se verifica si C es un camino en el grafo desde el nodo A al Z. Por ejemplo,

?- camino(sevilla,granada,C).
C = [sevilla, córdoba, granada] ;
C = [sevilla, málaga, córdoba, granada] 
Yes

camino(A,Z,C) :-
   camino_aux(A,[Z],C).

camino_aux(+A,+CP,-C) se verifica si C es una camino en el grafo compuesto de un camino desde A hasta el primer elemento del camino parcial CP (con nodos distintos a los de CP) junto CP.

camino_aux(A,[A|C1],[A|C1]).
camino_aux(A,[Y|C1],C) :-
   adyacente(X,Y),
   not(member(X,[Y|C1])),
   camino_aux(A,[X,Y|C1],C).

5.3 Caminos hamiltonianos en un grafo

hamiltoniano(-C) se verifica si C es un camino hamiltoniano en el grafo (es decir, es un camino en el grafo que pasa por todos sus nodos una vez). Por ejemplo,

?- hamiltoniano(C).
C = [almería, jaén, granada, córdoba, málaga, sevilla, huelva, cádiz] 
?- findall(_C,hamiltoniano(_C),_L), length(_L,N).
N = 16

Primera definición de hamiltoniano

hamiltoniano_1(C) :-
   camino(_,_,C),   
   nodos(L),        
   length(L,N),     
   length(C,N).

Segunda definición de hamiltoniano

hamiltoniano_2(C) :- 
   nodos(L),         
   length(L,N),      
   length(C,N),      
   camino(_,_,C).

Comparación de eficiencia

?- time(findall(_C,hamiltoniano_1(_C),_L)).
37,033 inferences in 0.03 seconds (1234433 Lips)
?- time(findall(_C,hamiltoniano_2(_C),_L)).
13,030 inferences in 0.01 seconds (1303000 Lips)

José A. Alonso Jiménez
Grupo de Lógica Computacional
Dpto. de Ciencias de la Computación e I.A.
Universidad de Sevilla